Математической моделью объекта называется. Общая схема принятия решения
Как систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого, исследование которых средствами математики должно ответить на поставленные вопросы о свойствах некоторой совокупности свойств объекта реального мира , как совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности, присущие изучаемому процессу, объекту или системе .
В автоматизированных системах управления математическая модель используется для определения алгоритма функционирования контроллера. Этот алгоритм определяет, как следует изменять управляющее воздействие в зависимости от изменения задающего для того, чтобы была достигнута цель управления.
Классификация моделей
Формальная классификация моделей
Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий . Например, один из популярных наборов дихотомий :
и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом - распределённые модели и т. д.
Классификация по способу представления объекта
Наряду с формальной классификацией, модели различаются по способу представления объекта:
- Структурные или функциональные модели
Модели-гипотезы в науке не могут быть доказаны раз и навсегда, можно лишь говорить об их опровержении или неопровержении в результате эксперимента .
Если модель первого типа построена, то это означает, что она временно признаётся за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.
Феноменологическая модель
Второй тип - феноменологическая модель («ведем себя так, как если бы…» ), содержит механизм для описания явления, хотя этот механизм недостаточно убедителен, не может быть достаточно подтверждён имеющимися данными или плохо согласуется с имеющимися теориями и накопленным знанием об объекте. Поэтому феноменологические модели имеют статус вре́менных решений. Считается, что ответ всё ещё неизвестен, и необходимо продолжить поиск «истинных механизмов». Ко второму типу Пайерлс относит, например, модели теплорода и кварковую модель элементарных частиц.
Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично новое знание может постепенно прийти в противоречие с моделями-гипотезами первого типа, и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешёл в первый тип. А вот модели эфира проделали путь от типа 1 к типу 2, а сейчас находятся вне науки.
Идея упрощения очень популярна при построении моделей. Но упрощение бывает разным. Пайерлс выделяет три типа упрощений в моделировании.
Приближение
Третий тип моделей - приближения («что-то считаем очень большим или очень малым» ). Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый приём в этом случае - использование приближений (моделей типа 3). Среди них модели линейного отклика . Уравнения заменяются линейными. Стандартный пример - закон Ома .
Мысленный эксперимент
m x ¨ = − k x {\displaystyle m{\ddot {x}}=-kx} ,где x ¨ {\displaystyle {\ddot {x}}} означает вторую производную от x {\displaystyle x} по времени: x ¨ = d 2 x d t 2 {\displaystyle {\ddot {x}}={\frac {d^{2}x}{dt^{2}}}} .
Полученное уравнение описывает математическую модель рассмотренной физической системы. Эта модель называется «гармоническим осциллятором ».
По формальной классификации эта модель линейная, детерминистская, динамическая, сосредоточенная, непрерывная. В процессе её построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т. д.), которые в реальности могут не выполняться.
По отношению к реальности это, чаще всего, модель типа 4 упрощение («опустим для ясности некоторые детали»), поскольку опущены некоторые существенные универсальные особенности (например, диссипация). В некотором приближении (скажем, пока отклонение груза от равновесия невелико, при малом трении, в течение не слишком большого времени и при соблюдении некоторых других условий), такая модель достаточно хорошо описывает реальную механическую систему, поскольку отброшенные факторы оказывают пренебрежимо малое влияние на её поведение. Однако модель можно уточнить, приняв во внимание какие-то из этих факторов. Это приведёт к новой модели, с более широкой (хотя и снова ограниченной) областью применимости.
Впрочем, при уточнении модели сложность её математического исследования может существенно возрасти и сделать модель фактически бесполезной. Зачастую более простая модель позволяет лучше и глубже исследовать реальную систему, чем более сложная (и, формально, «более правильная»).
Если применять модель гармонического осциллятора к объектам, далёким от физики, её содержательный статус может быть другим. Например, при приложении этой модели к биологическим популяциям её следует отнести, скорее всего, к типу 6 аналогия («учтём только некоторые особенности»).
Жёсткие и мягкие модели
Гармонический осциллятор - пример так называемой «жёсткой» модели. Она получена в результате сильной идеализации реальной физической системы. Свойства гармонического осциллятора качественно изменяются малыми возмущениями. Например, если добавить в правую часть малое слагаемое − ε x ˙ {\displaystyle -\varepsilon {\dot {x}}} (трение) ( ε > 0 {\displaystyle \varepsilon >0} - некоторый малый параметр), то получим экспоненциально затухающие колебания, если изменить знак добавочного слагаемого (ε x ˙) {\displaystyle (\varepsilon {\dot {x}})} то трение превратится в накачку и амплитуда колебаний будет экспоненциально возрастать.
Для решения вопроса о применимости жёсткой модели необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Нужно исследовать мягкие модели, получающиеся малым возмущением жёсткой. Для гармонического осциллятора они могут задаваться, например, следующим уравнением:
m x ¨ = − k x + ε f (x , x ˙) {\displaystyle m{\ddot {x}}=-kx+\varepsilon f(x,{\dot {x}})} .Здесь f (x , x ˙) {\displaystyle f(x,{\dot {x}})} - некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения. Явный вид функции f {\displaystyle f} нас в данный момент не интересует.
Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведётся к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований.
Если система сохраняет своё качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор - пример структурно-неустойчивой (негрубой) системы. Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.
Универсальность моделей
Важнейшие математические модели обычно обладают важным свойством универсальности : принципиально разные реальные явления могут описываться одной и той же математической моделью. Скажем, гармонический осциллятор описывает не только поведение груза на пружине, но и другие колебательные процессы, зачастую имеющие совершенно иную природу: малые колебания маятника, колебания уровня жидкости в U {\displaystyle U} -образном сосуде или изменение силы тока в колебательном контуре. Таким образом, изучая одну математическую модель, мы изучаем сразу целый класс описываемых ею явлений. Именно этот изоморфизм законов, выражаемых математическими моделями в различных сегментах научного знания, подвиг Людвига фон Берталанфи на создание «общей теории систем ».
Прямая и обратная задачи математического моделирования
Существует множество задач, связанных с математическим моделированием. Во-первых, надо придумать основную схему моделируемого объекта, воспроизвести его в рамках идеализаций данной науки. Так, вагон поезда превращается в систему пластин и более сложных тел из разных материалов, каждый материал задаётся как его стандартная механическая идеализация (плотность, модули упругости, стандартные прочностные характеристики), после чего составляются уравнения, по дороге какие-то детали отбрасываются как несущественные, производятся расчёты, сравниваются с измерениями, модель уточняется, и так далее. Однако для разработки технологий математического моделирования полезно разобрать этот процесс на основные составные элементы.
Традиционно выделяют два основных класса задач, связанных с математическими моделями: прямые и обратные.
Прямая задача : структура модели и все её параметры считаются известными, главная задача - провести исследование модели для извлечения полезного знания об объекте. Какую статическую нагрузку выдержит мост? Как он будет реагировать на динамическую нагрузку (например, на марш роты солдат, или на прохождение поезда на различной скорости), как самолёт преодолеет звуковой барьер, не развалится ли он от флаттера , - вот типичные примеры прямой задачи. Постановка правильной прямой задачи (задание правильного вопроса) требует специального мастерства. Если не заданы правильные вопросы, то мост может обрушиться, даже если была построена хорошая модель для его поведения. Так, в 1879 г. в Великобритании обрушился металлический Железнодорожный мост через Ферт-оф-Тей , конструкторы которого построили модель моста, рассчитали его на 20-кратный запас прочности на действие полезной нагрузки, но забыли о постоянно дующих в тех местах ветрах. И через полтора года он рухнул.
В простейшем случае (одно уравнение осциллятора, например) прямая задача очень проста и сводится к явному решению этого уравнения.
Обратная задача : известно множество возможных моделей, надо выбрать конкретную модель на основании дополнительных данных об объекте. Чаще всего структура модели известна, и необходимо определить некоторые неизвестные параметры. Дополнительная информация может состоять в дополнительных эмпирических данных, или в требованиях к объекту (задача проектирования ). Дополнительные данные могут поступать независимо от процесса решения обратной задачи (пассивное наблюдение ) или быть результатом специально планируемого в ходе решения эксперимента (активное наблюдение ).
Одним из первых примеров виртуозного решения обратной задачи с максимально полным использованием доступных данных был построенный Ньютоном метод восстановления сил трения по наблюдаемым затухающим колебаниям.
В качестве другого примера можно привести математическую статистику . Задача этой науки - разработка методов регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений . То есть множество возможных моделей ограничено вероятностными моделями. В конкретных задачах множество моделей ограничено сильнее.
Компьютерные системы моделирования
Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple , Mathematica , Mathcad , MATLAB , VisSim и др. Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.
Дополнительные примеры
Модель Мальтуса
Согласно модели, предложенной Мальтусом , скорость роста пропорциональна текущему размеру популяции , то есть описывается дифференциальным уравнением:
x ˙ = α x {\displaystyle {\dot {x}}=\alpha x} ,где α {\displaystyle \alpha } - некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция x (t) = x 0 e α t {\displaystyle x(t)=x_{0}e^{\alpha t}} . Если рождаемость превосходит смертность ( α > 0 {\displaystyle \alpha >0} ), размер популяции неограниченно и очень быстро возрастает. В действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестаёт быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель , которая описывается дифференциальным уравнением Ферхюльста :
x ˙ = α (1 − x x s) x {\displaystyle {\dot {x}}=\alpha \left(1-{\frac {x}{x_{s}}}\right)x} ,где - «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению x s {\displaystyle x_{s}} , причём такое поведение структурно устойчиво.
Система хищник-жертва
Допустим, что на некоторой территории обитают два вида животных : кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов x {\displaystyle x} , число лис y {\displaystyle y} . Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки - Вольтерры :
{ x ˙ = (α − c y) x y ˙ = (− β + d x) y {\displaystyle {\begin{cases}{\dot {x}}=(\alpha -cy)x\\{\dot {y}}=(-\beta +dx)y\end{cases}}}Поведение данной системы не является структурно устойчивым : малое изменение параметров модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения .
При некоторых значениях параметров эта система имеет равновесное состояние , когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к постепенно затухающим колебаниям численности кроликов и лис.
Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведёт к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерры - Лотки ответа не даёт: здесь требуются дополнительные исследования.
См. также
Примечания
- «A mathematical representation of reality»(Encyclopaedia Britanica)
- Новик И. Б. , О философских вопросах кибернетического моделирования. М., Знание, 1964.
- Советов Б. Я., Яковлев С. А. , Моделирование систем: Учеб. для вузов - 3-е изд., перераб. и доп. - М.: Высш. шк., 2001. - 343 с. ISBN 5-06-003860-2
- Самарский А. А. , Михайлов А. П. Математическое моделирование. Идеи. Методы. Примеры . - 2-е изд., испр. - М. : Физматлит, 2001. - ISBN 5-9221-0120-X .
- Мышкис А. Д. , Элементы теории математических моделей. - 3-е изд., испр. - М.: КомКнига, 2007. - 192 с ISBN 978-5-484-00953-4
- Севостьянов, А. Г. Моделирование технологических процессов: учебник / А. Г. Севостьянов, П. А. Севостьянов. - М.: Легкая и пищевая промышленность, 1984. - 344 с.
- Ротач В.Я. Теория автоматического управления. - 1-е. - М. : ЗАО "Издательский дом МЭИ", 2008. - С. 333. - 9 с. - ISBN 978-5-383-00326-8 .
- Model Reduction and Coarse-Graining Approaches for Multiscale Phenomena (англ.) . Springer, Complexity series, Berlin-Heidelberg-New York, 2006. XII+562 pp. ISBN 3-540-35885-4 . Дата обращения 18 июня 2013. Архивировано 18 июня 2013 года.
- «Теория считается линейной или нелинейной в зависимости от того, какой - линейный или нелинейный - математический аппарат, какие - линейные или нелинейные - математические модели она использует. … ез отрицание последней. Современный физик, доведись ему заново создавать определение столь важной сущности, как нелинейность, скорее всего, поступил бы иначе, и, отдав предпочтение нелинейности как более важной и распространенной из двух противоположностей, определил бы линейность как „не нелинейность“.» Данилов Ю. А. , Лекции по нелинейной динамике. Элементарное введение. Серия «Синергетика: от прошлого к будущему». Изд.2. - M.: URSS, 2006. - 208 с. ISBN 5-484-00183-8
- «Динамические системы, моделируемые конечным числом обыкновенных дифференциальных уравнений, называют сосредоточенными или точечными системами. Они описываются с помощью конечномерного фазового пространства и характеризуются конечным числом степеней свободы. Одна и та же система в различных условиях может рассматриваться либо как сосредоточенная, либо как распределенная. Математические модели распределенных систем - это дифференциальные уравнения в частных производных, интегральные уравнения или обыкновенные уравнения с запаздывающим аргументом. Число степеней свободы распределенной системы бесконечно, и требуется бесконечное число данных для определения её состояния.»
Анищенко В. С. , Динамические системы, Соросовский образовательный журнал, 1997, № 11, с. 77-84. - «В зависимости от характера изучаемых процессов в системе S все виды моделирования могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные. Детерминированное моделирование отображает детерминированные процессы, то есть процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероятностные процессы и события. … Статическое моделирование служит для описания поведения объекта в какой-либо момент времени, а динамическое моделирование отражает поведение объекта во времени. Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, а дискретно-непрерывное моделирование используется для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.»
Советов Б. Я., Яковлев С. А. , Моделирование систем: Учеб. для вузов - 3-е изд., перераб. и доп. - М.: Высш. шк., 2001. - 343 с. ISBN 5-06-003860-2 - Обычно в математической модели отражается структура (устройство) моделируемого объекта, существенные для целей исследования свойства и взаимосвязи компонентов этого объекта; такая модель называется структурной. Если же модель отражает только то, как объект функционирует - например, как он реагирует на внешние воздействия,- то она называется функциональной или, образно, чёрным ящиком. Возможны и модели комбинированного типа. Мышкис А. Д. , Элементы теории математических моделей. - 3-е изд., испр. - М.: КомКнига, 2007. - 192 с
Математическое моделирование
1. Что такое математическое моделирование?
С середины XX в. в самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, как «математическая экономика», «математическая химия», «математическая лингвистика» и т. д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.
Математическая модель - это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования - исследовать эти объекты и предсказать результаты будущих наблюдений. Однако моделирование - это еще и метод познания окружающего мира, дающий возможность управлять им.
Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории, чтобы проверить, «что было бы, если бы...» Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.
2. Основные этапы математического моделирования
1) Построение модели . На этом этапе задается некоторый «нематематический» объект - явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.
2) Решение математической задачи, к которой приводит модель . На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.
3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.
4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.
5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.
3. Классификация моделей
Классифицировать модели можно по разным критериям. Например, по характеру решаемых проблем модели могут быть разделены на функциональные и структурные. В первом случае все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие - как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа (дифференциальных, алгебраических и т. д.), устанавливающих количественные зависимости между рассматриваемыми величинами. Во втором случае модель характеризует структуру сложного объекта, состоящего из отдельных частей, между которыми существуют определенные связи. Как правило, эти связи не поддаются количественному измерению. Для построения таких моделей удобно использовать теорию графов. Граф - это математический объект, представляющий собой некоторое множество точек (вершин) на плоскости или в пространстве, некоторые из которых соединены линиями (ребрами).
По характеру исходных данных и результатов предсказания модели могут быть разделены на детерминистические и вероятностно-статистические. Модели первого типа дают определенные, однозначные предсказания. Модели второго типа основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер.
4. Примеры математических моделей
1) Задачи о движении снаряда.
Рассмотрим следующую задачу механики.
Снаряд пущен с Земли с начальной скоростью v 0 = 30 м/с под углом a = 45° к ее поверхности; требуется найти траекторию его движения и расстояние S между начальной и конечной точкой этой траектории.
Тогда, как это известно из школьного курса физики, движение снаряда описывается формулами:
где t - время, g = 10 м/с 2 - ускорение свободного падения. Эти формулы и дают математическую модель поставленной задачи. Выражая t через x из первого уравнения и подставляя во второе, получим уравнение траектории движения снаряда:

Эта кривая (парабола) пересекает ось x в двух
точках: x 1 = 0 (начало траектории) и  (место падения
снаряда). Подставляя в полученные формулы
заданные значения v0 и a, получим
(место падения
снаряда). Подставляя в полученные формулы
заданные значения v0 и a, получим
ответ: y = x – 90x 2 , S = 90 м.
Отметим, что при построении этой модели использован ряд предположений: например, считается, что Земля плоская, а воздух и вращение Земли не влияют на движение снаряда.
2) Задача о баке с наименьшей площадью поверхности.
Требуется найти высоту h 0 и радиус r 0 жестяного бака объема V = 30 м 3 , имеющего форму закрытого кругового цилиндра, при которых площадь его поверхности S минимальна (в этом случае на его изготовление пойдет наименьшее количество жести).
Запишем следующие формулы для объема и площади поверхности цилиндра высоты h и радиуса r:
V = p r 2 h, S = 2p r(r + h).
Выражая h через r и V из первой формулы и подставляя полученное выражение во вторую, получим:
![]()
Таким образом, с математической точки зрения, задача сводится к определению такого значения r, при котором достигает своего минимума функция S(r). Найдем те значения r 0 , при которых производная
![]()
обращается в ноль:Можно проверить, что вторая производная
функции S(r) меняет знак с минуса на плюс при
переходе аргумента r через точку r 0 .
Следовательно, в точке r0 функция S(r) имеет
минимум. Соответствующее значение h 0 = 2r 0 .
Подставляя в выражение для r 0 и h 0
заданное значение V, получим искомый радиус и высоту ![]()
3) Транспортная задача.
В городе имеются два склада муки и два хлебозавода. Ежедневно с первого склада вывозят 50 т муки, а со второго - 70 т на заводы, причем на первый - 40 т, а на второй - 80 т.
Обозначим через a ij стоимость перевозки 1 т муки с i-го склада на j-й завод (i, j = 1,2). Пусть
a 11 = 1,2 р., a 12 = 1,6 р., a 21 = 0,8 р., a 22 = 1 р.
Как нужно спланировать перевозки, чтобы их стоимость была минимальной?
Придадим задаче математическую формулировку. Обозначим через x 1 и x 2 количество муки, которое надо перевезти с первого склада на первый и второй заводы, а через x 3 и x 4 - со второго склада на первый и второй заводы соответственно. Тогда:
x 1 + x 2 = 50, x 3 + x 4 = 70, x 1 + x 3 = 40, x 2 + x 4 = 80. (1)
Общая стоимость всех перевозок определяется формулой
f = 1,2x 1 + 1,6x 2 + 0,8x 3 + x 4 .
С математической точки зрения, задача заключается в том, чтобы найти четыре числа x 1 , x 2 , x 3 и x 4 , удовлетворяющие всем заданным условиям и дающим минимум функции f. Решим систему уравнений (1) относительно xi (i = 1, 2, 3, 4) методом исключения неизвестных. Получим, что
x 1 = x 4 – 30, x 2 = 80 – x 4 , x 3 = 70 – x 4 , (2)
а x 4 не может быть определено однозначно. Так как x i і 0 (i = 1, 2, 3, 4), то из уравнений (2) следует, что 30Ј x 4 Ј 70. Подставляя выражение для x 1 , x 2 , x 3 в формулу для f, получим
f = 148 – 0,2x 4 .
Легко видеть, что минимум этой функции достигается при максимально возможном значении x 4 , то есть при x 4 = 70. Соответствующие значения других неизвестных определяются по формулам (2): x 1 = 40, x 2 = 10, x 3 = 0.
4) Задача о радиоактивном распаде.
Пусть N(0) - исходное количество атомов
радиоактивного вещества, а N(t) - количество
нераспавшихся атомов в момент времени t.
Экспериментально установлено, что скорость
изменения количества этих атомов N"(t)
пропорциональна N(t), то есть N"(t)=–l
N(t),
l
>0 - константа
радиоактивности данного вещества. В школьном
курсе математического анализа показано, что
решение этого дифференциального уравнения имеет
вид N(t) = N(0)e –l
t . Время T, за
которое число исходных атомов уменьшилось вдвое,
называется периодом полураспада, и является
важной характеристикой радиоактивности
вещества. Для определения T надо положить в
формуле Тогда ![]() Например, для
радона l
= 2,084 ·
10 –6 ,
и следовательно, T = 3,15 сут.
Например, для
радона l
= 2,084 ·
10 –6 ,
и следовательно, T = 3,15 сут.
5) Задача о коммивояжере.
Коммивояжеру, живущему в городе A 1 , надо посетить города A 2 , A 3 и A 4 , причем каждый город точно один раз, и затем вернуться обратно в A 1 . Известно, что все города попарно соединены между собой дорогами, причем длины дорог b ij между городами A i и A j (i, j = 1, 2, 3, 4) таковы:
b 12 = 30, b 14 = 20, b 23 = 50, b 24 = 40, b 13 = 70, b 34 = 60.
 Надо
определить порядок посещения городов, при
котором длина соответствующего пути минимальна.
Надо
определить порядок посещения городов, при
котором длина соответствующего пути минимальна.
Изобразим каждый город точкой на плоскости и пометим ее соответствующей меткой Ai (i = 1, 2, 3, 4). Соединим эти точки отрезками прямых: они будут изображать дороги между городами. Для каждой «дороги» укажем ее протяженность в километрах (рис. 2). Получился граф - математический объект, состоящий из некоторого множества точек на плоскости (называемых вершинами) и некоторого множества линий, соединяющих эти точки (называемых ребрами). Более того, этот граф меченый, так как его вершинам и ребрам приписаны некоторые метки - числа (ребрам) или символы (вершинам). Циклом на графе называется последовательность вершин V 1 , V 2 , ..., V k , V 1 такая, что вершины V 1 , ..., V k - различны, а любая пара вершин V i , V i+1 (i = 1, ..., k – 1) и пара V 1 , V k соединены ребром. Таким образом, рассматриваемая задача заключается в отыскании такого цикла на графе, проходящего через все четыре вершины, для которого сумма всех весов ребер минимальна. Найдем перебором все различные циклы, проходящие через четыре вершины и начинающиеся в A 1:
1) A 1 , A 4 , A 3 , A 2 , A 1 ;
2) A 1 , A 3 , A 2 , A 4 , A 1 ;
3) A 1 , A 3 , A 4 , A 2 , A 1 .
Найдем теперь длины этих циклов (в км): L 1 = 160, L 2 = 180, L 3 = 200. Итак, маршрут наименьшей длины - это первый.
Заметим, что если в графе n вершин и все вершины попарно соединены между собой ребрами (такой граф называется полным), то число циклов, проходящих через все вершины, равно Следовательно, в нашем случае имеется ровно три цикла.
6) Задача о нахождении связи между структурой и свойствами веществ.
 Рассмотрим
несколько химических соединений, называемых
нормальными алканами. Они состоят из n атомов
углерода и n + 2 атомов водорода (n = 1, 2 ...), связанных
между собой так, как показано на рисунке 3 для n = 3.
Пусть известны экспериментальные значения
температур кипения этих соединений:
Рассмотрим
несколько химических соединений, называемых
нормальными алканами. Они состоят из n атомов
углерода и n + 2 атомов водорода (n = 1, 2 ...), связанных
между собой так, как показано на рисунке 3 для n = 3.
Пусть известны экспериментальные значения
температур кипения этих соединений:
y э (3) = – 42°, y э (4) = 0°, y э (5) = 28°, y э (6) = 69°.
Требуется найти приближенную зависимость между температурой кипения и числом n для этих соединений. Предположим, что эта зависимость имеет вид
y » a n + b,
где a , b - константы, подлежащие определению. Для нахождения a и b подставим в эту формулу последовательно n = 3, 4, 5, 6 и соответствующие значения температур кипения. Имеем:
– 42 » 3a + b, 0 » 4a + b, 28 » 5a + b, 69 » 6a + b.
Для определения наилучших a и b существует много разных методов. Воспользуемся наиболее простым из них. Выразим b через a из этих уравнений:
b » – 42 – 3a , b » – 4a , b » 28 – 5a , b » 69 – 6a .
Возьмем в качестве искомого b среднее арифметическое этих значений, то есть положим b » 16 – 4,5a . Подставим в исходную систему уравнений это значение b и, вычисляя a , получим для a следующие значения: a » 37, a » 28, a » 28, a » 36. Возьмем в качестве искомого a среднее значение этих чисел, то есть положим a » 34. Итак, искомое уравнение имеет вид
y » 34n – 139.
Проверим точность модели на исходных четырех соединениях, для чего вычислим температуры кипения по полученной формуле:
y р (3) = – 37°, y р (4) = – 3°, y р (5) = 31°, y р (6) = 65°.
Таким образом, ошибка расчетов данного свойства для этих соединений не превышает 5°. Используем полученное уравнение для расчета температуры кипения соединения с n = 7, не входящего в исходное множество, для чего подставим в это уравнение n = 7: y р (7) = 99°. Результат получился довольно точный: известно, что экспериментальное значение температуры кипения y э (7) = 98°.
7) Задача об определении надежности электрической цепи.
Здесь мы рассмотрим пример вероятностной модели. Сначала приведем некоторые сведения из теории вероятностей - математической дисциплины, изучающей закономерности случайных явлений, наблюдаемых при многократном повторении опыта. Назовем случайным событием A возможный исход некоторого опыта. События A 1 , ..., A k образуют полную группу, если в результате опыта обязательно происходит одно из них. События называются несовместными, если они не могут произойти одновременно в одном опыте. Пусть при n-кратном повторении опыта событие A произошло m раз. Частотой события A называется число W = . Очевидно, что значение W нельзя предсказать точно до проведения серии из n опытов. Однако природа случайных событий такова, что на практике иногда наблюдается следующий эффект: при увеличении числа опытов значение практически перестает быть случайным и стабилизируется около некоторого неслучайного числа P(A), называемого вероятностью события A. Для невозможного события (которое никогда не происходит в опыте) P(A)=0, а для достоверного события (которое всегда происходит в опыте) P(A)=1. Если события A 1 , ..., A k образуют полную группу несовместимых событий, то P(A 1)+...+P(A k)=1.
Пусть, например, опыт состоит в подбрасывании игральной кости и наблюдении числа выпавших очков X. Тогда можно ввести следующие случайные события A i ={X = i}, i = 1, ..., 6. Они образуют полную группу несовместных равновероятных событий, поэтому P(A i) = (i = 1, ..., 6).
Суммой событий A и B называется событие A + B, состоящее в том, что в опыте происходит хотя бы одно из них. Произведением событий A и B называется событие AB, состоящее в одновременном появлении этих событий. Для независимых событий A и B верны формулы
P(AB) = P(A) P(B), P(A + B) = P(A) + P(B).
8) Рассмотрим теперь следующую задачу . Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны P 1 = 0,1, P 2 = 0,15, P 3 = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли данная цепь надежной.
Так как элементы включены последовательно, то тока в цепи не будет (событие A), если откажет хотя бы один из элементов. Пусть A i - событие, заключающееся в том, что i-й элемент работает (i = 1, 2, 3). Тогда P(A1) = 0,9, P(A2) = 0,85, P(A3) = 0,8. Очевидно, что A 1 A 2 A 3 - событие, заключающееся в том, что одновременно работают все три элемента, и
P(A 1 A 2 A 3) = P(A 1) P(A 2) P(A 3) = 0,612.
Тогда P(A) + P(A 1 A 2 A 3) = 1, поэтому P(A) = 0,388 < 0,4. Следовательно, цепь является надежной.
В заключение отметим, что приведенные примеры математических моделей (среди которых есть функциональные и структурные, детерминистические и вероятностные) носят иллюстративный характер и, очевидно, не исчерпывают всего разнообразия математических моделей, возникающих в естественных и гуманитарных науках.
ЭВМ прочно вошла в нашу жизнь, и практически нет такой области человеческой деятельности, где не применялась бы ЭВМ. ЭВМ сейчас широко используется в процессе создания и исследования новых машин, новых технологических процессов и поиске их оптимальных вариантов; при решении экономических задач, при решении задач планирования и управления производством на различных уровнях. Создание же крупных объектов в ракетотехнике, авиастроении, судостроении, а также проектирование плотин, мостов, и др. вообще невозможно без применения ЭВМ.
Для использования ЭВМ при решении прикладных задач, прежде всего прикладная задача должна быть "переведена" на формальный математический язык, т.е. для реального объекта, процесса или системы должна быть построена его математическая модель.
Слово "Модель" происходит от латинского modus (копия, образ, очертание). Моделирование - это замещение некоторого объекта А другим объектом Б. Замещаемый объект А называется оригиналом или объектом моделирования, а замещающий Б - моделью. Другими словами, модель - это объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.
Целью моделирования являются получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; а модель здесь выступает как средство познания свойств и закономерности поведения объекта.
Математическое моделирование - это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью ЭВМ.
Математическое моделирование - процесс построения и изучения математических моделей реальных процессов и явлений. Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его моделью и затем изучают последнюю. Как и в случае любого моделирования, математическая модель не описывает полностью изучаемое явление, и вопросы о применимости полученных таким образом результатов являются весьма содержательными. Математическая модель - это упрощенное описание реальности с помощью математических понятий.
Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств. Собственно говоря, сама математика обязана своим существованием тому, что она пытается отразить, т.е. промоделировать, на своем специфическом языке закономерности окружающего мира.
При математическом моделировании исследование объекта осуществляется посредством модели, сформулированной на языке математики с использованием тех или иных математических методов.
Путь математического моделирования в наше время гораздо более всеобъемлющ, нежели моделирования натурного. Огромный толчок развитию математического моделирования дало появление ЭВМ, хотя сам метод зародился одновременно с математикой тысячи лет назад.
Математическое моделирование как таковое отнюдь не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т.е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Возможности аналитических методов решения сложных математических задач, однако, очень ограниченны и, как правило, эти методы гораздо сложнее численных.
Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи
Все модели можно разделить на два класса:
- вещественные,
- идеальные.
В свою очередь вещественные модели можно разделить на:
- натурные,
- физические,
- математические.
Идеальные модели можно разделить на:
- наглядные,
- знаковые,
- математические.
Вещественные натурные модели - это реальные объекты, процессы и системы, над которыми выполняются эксперименты научные, технические и производственные.
Вещественные физические модели - это макеты, муляжи, воспроизводящие физические свойства оригиналов (кинематические, динамические, гидравлические, тепловые, электрические, световые модели).
Вещественные математические - это аналоговые, структурные, геометрические, графические, цифровые и кибернетические модели.
Идеальные наглядные модели - это схемы, карты, чертежи, графики, графы, аналоги, структурные и геометрические модели.
Идеальные знаковые модели - это символы, алфавит, языки программирования, упорядоченная запись, топологическая запись, сетевое представление.
Идеальные математические модели - это аналитические, функциональные, имитационные, комбинированные модели.
В приведенной классификации некоторые модели имеют двойное толкование (например - аналоговые). Все модели, кроме натурных, можно объединить в один класс мысленных моделей, т.к. они являются продуктом абстрактного мышления человека.
Элементы теории игры
В общем случае решение игры представляет довольно трудную задачу, причем сложность задачи и объем необходимых для решения вычислений резко возрастает с увеличением . Однако это трудности не носят принципиального характера и связаны только сочень большим объемом расчетов, который в ряде случаев может оказаться практически невыполнимым. Принципиальная сторона метода отыскания решения остается при любом одной и той же.
Проиллюстрируем это на примере игры . Дадим ей геометрическую интерпретацию - уже пространственную. Три наши стратегии , изобразим тремя точками на плоскости ; первая лежит в начале координат (рис.1). вторая и третья - на осях Ох и Оу на расстояниях 1 от начала.

Через точки проводятся оси I-I, II-II и III-III, перпендикулярные к плоскости . На оси I-I откладываются выигрыши при стратегии на осях II-II и III-III - выигрыши при стратегиях . Каждая стратегия противника изобразится плоскостью, отсекающей на осях I-I, II-II и III-III, отрезки, равные выигрышам
при соответствующих стратегия и стратегия . Построив, таким образом, все стратегии противника, мы получим семейство плоскостей над треугольником (рис2) .

Для этого семейства также можно построить нижнюю границу выигрыша, как мы это делали в случае, и найти на этой границе точку N с максимальной высотой нал плоскостью . Эта высота и будет ценой игры .
Частоты стратегий в оптимальной стратегии будут определяться координатами (x, у) точки N, а именно:
Однако такое геометрическое построение даже для случая нелегко осуществимо и требует большой затраты времени и усилий воображения. В общем же случае игры оно переносится в - мерное пространство и теряет всякую наглядность, хотя употребление геометрической терминологии в ряде случаев может оказаться полезным. При решении игр на практике удобнее пользоваться не геометрическими аналогиями, а расчетными аналитическими методами, тем более, что для решения задачи на вычислительных машинах эти методы единственно пригодны.
Все эти методы по существу сводятся к решению задачи путем последовательных проб, но упорядочение последовательности проб позволяет построить алгоритм, приводящий к решению наиболее экономичным способом.
Здесь мы вкратце остановимся на одном расчетном методе решения игр - на так называемом методе «линейного программирования».
Для этого дадим сначала общую постановку задачи о нахождении решения игры . Пусть дана игра с т стратегиями игрока А и n стратегиями игрока В и задана платежная матрица
Требуется найти решение игры, т. е. две оптимальные смешанные стратегии игроков А и В
где (некоторые из чисел и могут быть равными нулю).
Наша оптимальная стратегия S* A должна обеспечивать нам выигрыш, не меньший , при любом поведении противника, и выигрыш, равный , при его оптимальном поведении (стратегия S* B ).Аналогично стратегия S* B должна обеспечивать противнику проигрыш, не больший , при любом нашем поведении и равный при нашем оптимальном поведении (стратегия S* A ).
Величина цены игры в данном случае нам неизвестна; будем считать, что она равна некоторому положительному числу. Полагая так, мы не нарушаем общности рассуждений; для того чтобы было > 0, очевидно, достаточно, чтобы все элементы матрицы были неотрицательными. Этого всегда можно добиться, прибавляя к элементам достаточно большую положительную величину L;при этом цена игры увеличится на L, а решение не изменится.
Пусть мы выбрали свою оптимальную стратегию S* A . Тогда наш средний выигрыш при стратегии противника будет равен:
Наша оптимальная стратегия S* A обладает тем свойством, что при любом поведении противника обеспечивает выигрыш не меньший, чем ; следовательно, любое из чисел не может быть меньше . Получаем ряд условий:
 (1)
(1)
Разделим неравенства (1) на положительную величину и обозначим:
Тогда условие (1) запишется виде
 (2)
(2)
где - неотрицательные числа. Так как ![]() величины удовлетворяют условию
величины удовлетворяют условию
Мы хотим сделать свой гарантированный выигрыш максимально возможным; очевидно, при этом правая часть равенства (3) принимает минимальное значение.
Таким образом, задача нахождения решения игры сводится к следующей математической задаче: определить неотрицательные величины , удовлетворяющие условиям (2), так, чтобы их сумма
была минимальной.
Обычно при решении задач, связанных с нахождением экстремальных значений (максимумов и минимумов), функцию дифференцируют и приравнивают производные нулю. Но такой прием в данном случае бесполезен, так как функция Ф, которую нужно обратить в минимум, линейна, и ее производные по всем аргументам равны единице, т. е. нигде не обращаются в нуль. Следовательно, максимум функции достигается где-то на границе области изменения аргументов, которая определяется требованием неотрицательности аргументов и условиями (2). Прием нахождения экстремальных значений при помощи дифференцирования непригоден и в тех случаях, когда для решения игры определяется максимум нижней (или минимум верхней) границы выигрыша, как мы. например, делали при решении игр .Действительно, нижняя граница составлена из участков прямых линий, и максимум достигается не в точке, где производная равна нулю (такой точки вообще нет), а на границе интервала или в точке пересечения прямолинейных участков.
Для решения подобных задач, довольно часто встречающихся на практике, в математике разработан специальный аппарат линейного программирования.
Задача линейного программирования ставится следующим образом.
Дана система линейных уравнений:
 (4)
(4)
Требуется найти неотрицательные значения величин удовлетворяющие условиям (4) и вместе с тем обращающие в минимум заданную однородную линейную функцию величин (линейную форму):
Легко убедиться, что поставленная выше задача теории игр является частным случаем задачи линейного программирование при ![]()
С первого взгляда может показаться, что условия (2) не эквивалентны условиям (4), так как вместо знаков равенства они содержат знаки неравенства. Однако от знаков неравенства легко избавиться, вводя новые фиктивные неотрицательные переменные и записывая условия (2) в виде:
 (5)
(5)
Форма Ф, которую нужно обратить в минимум, равна
Аппарат линейного программирования позволяет путем сравнительно небольшого числа последовательных проб подобрать величины , удовлетворяющие поставленным требованиям. Для большей ясности мы здесь продемонстрируем применение этого аппарата прямо на материале решения конкретных игр.
Математическая модель - это абстракция реального мира, в которой интересующие исследователя отношения между реальными элементами заменены подходящими отношениями между математическими объектами. Математические модели, в описании которых используются случайные величины, называют вероятностными или стохастическими. Всякая модель является упрощенным представлением действительности, и искусство моделирования состоит в знании того, что, где, когда и как можно и нужно упростить. Это знание естественно приходит с опытом.
Следующий пример поможет читателю «прочувствовать» ряд узловых моментов и некоторые общие «тонкие места», с которыми приходится сталкиваться исследователю в процессе реалистического моделирования.
Рассмотрим эксперимент, в котором каждый из испытуемых прочитывает текст, набранный шрифтом А, и эквивалентный ему по трудности текст, набранный шрифтом Б. В обоих случаях фиксируется время затрачиваемое испытуемым на чтение. Пусть - время, потребовавшееся испытуемому на чтение контрольных текстов, набранных соответственно шрифтами А и Б. Один из возможных простых вариантов математической модели данной ситуации может быть описан следующим образом:

где - случайная величина, отражающая скорость чтения испытуемого и не зависящая от шрифта, - постоянные, зависящие только от шрифта, a - взаимно независимые случайные ошибки со средними значениями, равными нулю, и с одинаковыми дисперсиями . В правую часть уравнений (3.1) входит больше величин, чем в левую. Это означает, что оценить основные числовые характеристики величин , и по наблюдениям нельзя. Более того, даже при отсутствии в модели ошибок и , т. е. в ситуации, когда в левой части величин, а в правой - только найти без дополнительных соглашений величины и основные числовые характеристики случайных величин также нельзя. (В подобных случаях иногда принято говорить, что модель неизмерима относительно имеющихся опытных данных.) Однако, если в задачу исследования входит только сравнение средней скорости чтения двух анализируемых шрифтов, то неизмеримость модели нам не мешает. В самом деле, случайная величина
имеет положительное среднее значение, если шрифт Б более удобен для чтения, чем шрифт А, и отрицательное среднее значение - в противном случае.
Оценка же разности по значениям уже не представляет труда. Аналогично, если бы нам требовалось охарактеризовать меру случайного разброса в скорости чтения каждого из испытуемых (т. е. оценить дисперсию , ее определение и вычисление см. в гл. 5 и 8), мы могли бы найти дисперсию случайных величин
и вычесть из нее величину определяющую вклад случайных ошибок в модели (3.3). В данном случае дисперсию мы оцениваем, не определяя для каждого испытуемого, а воспользовавшись тем, что - постоянные.
Таким образом, с помощью различных вариантов моде» ли (3.1) можно учесть: различие между испытуемыми, в скорости чтения; различие между средней скоростью чтения шрифтов А и Б; случайный характер времени, затрачиваемого испытуемым на чтение текста. Вместе с тем в ней пренебрегается возможной зависимостью разности от скорости чтения индивидуума () и от того, в какой последовательности прочитываются тексты: сначала А, а затем Б или наоборот. Кроме того, упрощением является и предположение о постоянстве дисперсий случайных погрешностей. Безусловно, для более тщательного изучения длительности чтения потребовалась бы более сложная модель, в которой должны были бы найти отражение указанные выше зависимости. Однако, если речь идет только о сравнении средних скоростей чтения шрифтов, то достаточно рассмотреть модель (3.2) - она свою роль выполняет: подсказывает достаточно эффективный способ анализа данных, отвергая при этом другой возможный (и слишком наивный) подход, при котором сначала усредняются в отдельности данные по каждому шрифту:
а затем производится сравнение средних , полученных якобы по двум независимым сериям наблюдений (это сравнение может быть осуществлено, например, с помощью критерия Стьюдента, см. п. 11.2.8). Последний метод на практике может привести к резкой потере эффективности выявления существующего различия между шрифтами, так как наблюдения оказываются на самом деле существенно зависимыми из-за общего значения
В некотором смысле математическая модель является для исследователя тем же, чем для физика физическая лаборатория. Можно ставить эксперименты в «мире», порожденном моделью, и, если математическая модель является правдивым отражением действительности, результаты этих экспериментов применимы к реальному миру.
Говоря о применимости моделей к описанию реальной действительности, мы подразумеваем возможность их практического использования в качестве базы, отправной точки при выборе наилучшего способа статистической обработки исходных данных, а также при решении таких задач, как планирование, прогнозирование, оптимальное управление системами и процессами, оценка эффективности функционирования (или комплексной характеристики качества) сложной системы, диагностика (медицинская и техническая), нормирование.

В общем случае, модель – это отражение реального объекта. Такое отражение объекта может быть представлено эскизом, схемой, фотографией, графиком, таблицей и т.д.
Мы будем рассматривать только математические модели различных экономических процессов, которые описываются математической символикой и решаются с помощью соответствующих математических методов.
В экономической науке используют главным образом математические модели, описывающие изучаемое явление с помощью математического аппарата (функций, уравнений, неравенств, их систем).
В теории оптимальных решений главная роль отводится математическому моделированию. Для построения математической модели необходимо иметь строгое представление о цели функционирования исследуемой системы и располагать информацией об ограничениях, которые определяют область допустимых значений управляемых переменных. Как цель, так и ограничения должны быть представлены в виде функций от управляемых переменных. Анализ модели должен привести к определению наилучшего управляющего воздействия на объект управления при выполнении всех установленных ограничений.
Модель управляемого объекта строят для того, чтобы применить какой-либо вычислительный аппарат для оптимизации функционирования этого объекта (максимально возможного повышения эффективности его работы). Разработка модели почти всегда связана с попыткой достижения двух противоречивых целей: как можно точнее отобразить реальные процессы и получить модель максимально простую, чтобы с ней легко было работать.
Для применения количественных методов исследования экономических процессов требуется построить математическую модель объекта оптимизации. При построении модели объект, как правило, упрощается, схематизируется и схема объекта описывается с помощью того или иного математического аппарата.
Математическая модель – это приближенное описание какого-либо объекта или класса явлений внешнего мира, выраженное с помощью математического аппарата и математической символики.
Математические модели имеют ряд преимуществ перед другими видами моделей. К наиболее важным из них можно отнести следующие:
· широкий диапазон применения,
· низкая по сравнению с другими видами стоимость создания модели,
· быстрота получения результатов исследования при использовании электронно-вычислительной техники,
· возможность экспериментирования с исследуемым экономическим процессом,
· возможность проверки правильности выдвинутых предпосылок и условий поставленной экономической задачи.
Математическая модель любой экономической задачи включает в себя целевую функцию, систему ограничений и критерий оптимальности.
Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, себестоимость, рентабельность и т.д.). Поэтому целевую функцию иногда называют экономической, критериальной.
Целевая функция – характеристика объекта из условия дальнейшего поиска критерия оптимальности, математически связывающая между собой те или иные факторы объекта исследования.
При решении задач оптимизации необходимо определить критерий оптимальности, т.е. признак, по которому проводят сравнительную оценку альтернатив и выбирают среди них наилучшую с точки зрения поставленной цели оптимизации.
Критерий оптимальности – это показатель, имеющий, как правило, экономический смысл, который служит для формализации конкретной цели управления объектом исследования и выражается при помощи целевой функции.
Критерий оптимальности операции выполняет такую важную функцию как сравнительная оценка выбранных стратегий (решений) до начала их реализации и на завершающем этапе операции. Он позволяет провести анализ полученных результатов и сделать вывод о том, какая из стратегий была бы оптимальной.
Изменяемые при оптимизации величины, входящие в математическую модель объекта оптимизации, называют параметрами оптимизации , а соотношения, устанавливающие пределы возможного изменения этих параметров, - ограничениями .
Ограничения – это соотношения, сужающие область осуществимых, приемлемых или допустимых решений, и фиксирующие основные внешние и внутренние свойства объекта. Эти ограничения могут быть заданы в форме равенств или неравенств (или их систем).
Решением математической модели экономической задачи, или допустимым планом, называется набор значений неизвестных, который удовлетворяет ее системе ограничений. Модель может иметь множество решений, или допустимых планов, среди которых надо найти единственное, удовлетворяющее системе ограничений и целевой функции.
Допустимый план, удовлетворяющий целевой функции, называется оптимальным .
Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.
Таким образом , для принятия оптимального решения любой экономической задачи необходимо построить ее математическую модель, по структуре включающую в себя систему ограничений, целевую функцию, критерий оптимальности и решение.
Процесс построения математической модели называют математическим моделированием .
Составление модели объекта требует понимания сущности описываемого явления и знания математического аппарата.
Моделирование и построение математической модели экономического объекта позволяют свести экономический анализ производственных процессов к математическому анализу и принятию эффективных (оптимальных) решений.
При построении математической модели важно избежать, с одной стороны, чрезмерного упрощения экономического явления или процесса (т.к. излишнее упрощение не отражает реальной действительности), с другой стороны, - излишней его детализации и усложнения (т.к. это приводит к большому количеству переменных и затрудняет построение модели).
Основные элементы модели:
1) Исходные данные:
· детерминированные,
· случайные.
2) Искомые переменные:
· непрерывные,
· дискретные.
3) Зависимости:
· линейные (переменные входят в первой степени и нет их произведения),
· нелинейные (переменные входят в степени выше первой или есть произведение переменных).
Сочетание разнообразных элементов модели приводит к различным классам задач оптимизации (тема 2), требующим разных методов решения.
При решении конкретной экономической задачи применение методов оптимальных решений предполагает:
· построение математических моделей для задач принятия решения в сложных ситуациях или в условиях неопределенности,
· изучение взаимосвязей, определяющих впоследствии принятие решений, и установление критериев оптимальности, позволяющих оценивать преимущество того или иного варианта действия.
К основным методам принятия оптимальных решений можно отнести следующие:
1) Методы математического программирования:
· линейное программирование,
· нелинейное программирование,
· целочисленное программирование,
· динамическое программирование,
· выпуклое программирование,
· геометрическое программирование,
· параметрическое программирование
· стохастическое программирование,
· эвристическое программирование.
2) Методы теории массового обслуживания.
3) Методы теории игр.
4) Классические методы оптимизации (метод Лагранжа, градиентный метод).
5) Сетевые методы планирования и управления.
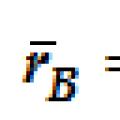 Сложение поступательного и вращательного движений
Сложение поступательного и вращательного движений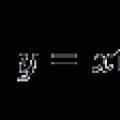 Общая схема принятия решения
Общая схема принятия решения Неусвоенные уроки карибского кризиса Поиски путей разрешения кризиса
Неусвоенные уроки карибского кризиса Поиски путей разрешения кризиса