Приближенные вычисления с помощью рядов. Разложение в ряд тейлора Приближенное решение задачи Коши для обыкновенного
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
,
где r n
– так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
![]() , где число x заключено между х и а.
, где число x заключено между х и а.
Правила ввода функций :
Если для некоторого значения х
r n
→0 при n
→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора
:
,
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
1) она имеет производные всех порядков;
2) построенный ряд сходится в этой точке.
При а =0 получаем ряд, называемый рядом Маклорена
:
,
Разложение простейших (элементарных) функций в ряд Маклорена:
Показательные функции
, R=∞
Тригонометрические функции
![]() , R=∞
, R=∞
![]() , R=∞
, R=∞
, (-π/2 < x < π/2), R=π/2
Функция actgx не разлагается по степеням x, т.к. ctg0=∞
Гиперболические функции
Логарифмические функции
, -1
Биномиальные ряды
![]() .
.
Пример №1
. Разложить в степенной ряд функцию f(x)=
2 x
.
Решение
. Найдем значения функции и ее производных при х
=0
f(x)
= 2 x
, f(0)
= 2 0
=1;
f"(x)
= 2 x
ln2, f"(0)
= 2 0
ln2= ln2;
f""(x)
= 2 x
ln 2 2, f""(0)
= 2 0
ln 2 2= ln 2 2;
…
f (n) (x)
= 2 x
ln n
2, f (n) (0)
= 2 0
ln n
2= ln n
2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:
Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x
<+∞.
Пример №2
. Написать ряд Тейлора по степеням (х
+4) для функции f(x)=
e x
.
Решение
. Находим производные функции e x
и их значения в точке х
=-4.
f(x)
= е x
, f(-4)
= е -4
;
f"(x)
= е x
, f"(-4)
= е -4
;
f""(x)
= е x
, f""(-4)
= е -4
;
…
f (n) (x)
= е x
, f (n) ( -4)
= е -4
.
Следовательно, искомый ряд Тейлора функции имеет вид:
Данное разложение также справедливо для -∞<x
<+∞.
Пример №3
. Разложить функцию f(x)
=lnx
в ряд по степеням (х-
1),
(т.е. в ряд Тейлора в окрестности точки х
=1).
Решение
. Находим производные данной функции.
f(x)=lnx , , , , ![]()
![]()
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(-1) n-1 (n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1 . Действительно,
Ряд сходится, если ½х-
1½<1, т.е. при 0<x
<2. При х
=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Пример №4
. Разложить в степенной ряд функцию .
Пример №5
. Разложить в ряд Маклорена функцию Замечание
.
Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось. Пример №5а
. Разложить в ряд Маклорена функцию , указать область сходимости.
Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Пример №6
. Разложить функцию в ряд Тейлора в окрестности точки х =3.
Пример №7
. Написать ряд Тейлора по степеням (х -1) функции ln(x+2) .
Пример №8
. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x =2.
Пример №1
. Вычислить ln(3) с точностью до 0,01.
Пример №2
. Вычислить с точностью до 0,0001.
Пример №3
. Вычислить интеграл ∫ 0 1 4 sin (x) x с точностью до 10 -5 .
Пример №4
. Вычислить интеграл ∫ 0 1 4 e x 2 с точностью до 0,001.
Пусть требуется найти У 2,35104 с точностью до (с недостатком). Расположим вычисления так: Мы сначала находим приближённый корень с точностью до 1 только из целого числа 2. Получим 1 (и в остатке 1). Пишем в корне цифру 1 и ставим после неё запятую. Теперь находим цифру десятых. Для этого приписываем к остатку 1 цифры 3 и 5, стоящие направо от запятой, и продолжаем извлечение так, как будто мы извлекали корень из целого числа 235. Полученную цифру 5 пишем в корне на месте десятых. Остальные цифры подкоренного числа (104) нам не нужны. Что полученное число 1,5 будет действительно приближённым корнем С точностью до видно наследующего; если бы мы находили наибольший целый корень из 235 с точностью до 1, то получили бы 15, значит, Разделив каждое из этих чисел на 100, получим; в, наконец, Пусть требуется найти с точностью до приближённый с недостатком. Найдём целое число, потом - цифру десятых, затем и цифру сотых. Корень из целого числа будет 15 целых. Чтобы получить цифру десятых, надо, как мы видели, приписать к остатку 23 еще две цифры, стоящие направо от запятой: В нашем примере этих цифр нет вовсе; ставим на их место нули. Приписав их к остатку и продолжая действие так, как будто находим корень из целого числа 24 800, мы найдём цифру десятых 7. Остаётся найти цифру сотых. Для этого приписываем к остатку 151 ещё два нуля и продолжаем извлечение, как будто мы находим корень из целого числа 2 480000. Получаем 15,74. Что это число действительно есть приближённый корень из 248 с точностью до с недостатком, видно из следующего. Если бы мы находили наибольший целый квадратный корень из целого числа 2 480 000, то получили бы 1574, значит, Разделив каждое из этих чисел на 10 000 (100^2), получим: Значит, 15,74 есть та десятичная дробь, которую мы назвали приближённым корнем с недостатком с точностью до из 248. Правило. Чтобы извлечь из данного целого числа или из данной десятичной дроби приближенный корень с недостатком с точностью до до до и т. д., находят сначала приближенный корень с недостатком с точностью до 1, извлекая корень из целого числа (если его нет, пишут в корне 0 целых). Потом находят цифру десятых. Для этого к остатку приписывают две цифры подкоренного числа, стоящие направо от запятой (если их нет, приписывают к остатку два нуля), и продолжают извлечение так, как это делается при извлечении корня из целого числа. Полученную цифру пишут в корне на месте десятых. Затем находят цифру сотых. Для этого к остатку приписывают снова две цифры, стоящие направо от тех, которые были только что снесены, и т. д. Таким образом, при извлечении корня из целого числа с десятичной дробью число надо делить на грани по две цифры в каждой, начиная от запятой, как влево (в целой части числа), так и вправо (в дробной части). 1. Извлечь с точностью до корни: 2. Извлечь с точностью до В последнем примере мы обратили дробь у в десятичную, вычислив восемь десятичных знаков, чтобы образовались четыре грани, потребные для нахождения четырёх десятичных знаков корня. Walter A. Aue / flickr.com Американские физики уточнили размерность пространства-времени, сравнив расстояние до источника, рассчитанное по затуханию гравитационных волн и по красному смещению электромагнитного излучения. Ученые выполнили такие расчеты для события GW170817 и выяснили, что размерность нашего пространства-времени примерно равна D
≈ 4,0 ± 0,1. Кроме того, они установили нижнюю границу на время жизни гравитона, которая составила около 450 миллионов лет. Препринт статьи выложен на сайте arXiv.org. Обновлено: в июле 2018 года статья была
опубликована
в Journal of Cosmology and Astroparticle Physics.
Общая теория относительности и Стандартная модель построены в предположении, что мы живем в четырехмерном пространстве-времени. Точнее, в (3+1)-мерном: 3 пространственных измерения и одно временно́е. С другой стороны, ученые склонны сомневаться в самых элементарных утверждениях. Может быть, размерность нашего пространства-времени не в точности равна четырем, а просто очень близка к этому значению? В самом деле, существуют теории , в которых наше пространство-время вложено в пространства с большей размерностью. Поэтому, вообще говоря, четырехмерность нашего мира нужно доказывать, а не принимать на веру. Группа физиков под руководством Дэвида Сперджела (David Spergel) установила точные ограничения на размерность нашего пространства-времени, анализируя - практически одновременно пришедшие на Землю гравитационные и электромагнитные волны, излученные во время слияния двух нейтронных звезд. С одной стороны, расстояние до источника волн можно определить по электромагнитной компоненты. С другой стороны, его можно рассчитать по затуханию гравитационных волн. Очевидно, оба этих расстояния должны совпасть, что накладывает ограничения на отличие скорости затухания от скорости, предсказанной ОТО. Стоит заметить, что дополнительную погрешность в расстояние, определенное по красному смещению, вносит тот факт, что значения постоянной Хаббла, измеренные по скорости разбегания галактик и по флуктуациям реликтового излучения, друг с другом. В данной статье ученые на всякий случай выполнили расчеты для обоих значений, однако погрешность экспериментальных данных все равно перевешивала эту разницу. В Общей теории относительности напряженность гравитационных волн спадает обратно пропорционально первой степени расстояния от источника: h
~ 1/r
. Однако в теориях с бо́льшим количеством измерений этот закон модифицируется , и затухание происходит быстрее: h
~ 1/r
γ , где γ = (D
− 2)/2, а D
- количество измерений. Получается, что энергия волны как будто «утекает» в дополнительные измерения. Вычисляя «электромагнитное» и «гравитационное» расстояние до нейтронных звезд, физики определили, что степень зависимости γ ≈ 1,00 ± 0,03, то есть размерность нашего пространства D
≈ 4,0 ± 0,1. Распределение вероятности того, что мы живем в D
-мерном пространстве. Линии разных цветов отвечают разным значениям постоянной Хаббла, используемой в расчетах С другой стороны, в еще одном типе альтернативных теорий гравитация экранируется - на маленьких расстояниях она ведет себя так же, как в четырехмерной теории, а на больших напоминает D
-мерную. Учитывая ограничения события GW170817, физики определили минимальный радиус экранирования таких теорий - он составил около двадцати мегапарсек. При этом собственно источник волн находится в галактике NGC 4993 на расстоянии около сорока мегапарсек. Наконец, дополнительное затухание гравитационных волн может возникнуть из-за того, что гравитоны являются нестабильными частицами и распадаются за время путешествия от источника до детектора. Отталкиваясь от этого предположения, физики вычислили нижнее ограничение на время жизни гравитона. Оказалось, что оно не может быть меньше 4,5×10 8 лет. Одновременная регистрация гравитационной и электромагнитной компоненты оказала большое влияние на альтернативные теории гравитации. Например, в конце декабря прошлого года в Physical Review Letters
одновременно вышло сразу четыре статьи , посвященные событию GW170817 и ограничениям на различные квантовые теории гравитации. Кроме того, это событие очень жесткие ограничение на скорость гравитации - теперь отношение скорости гравитации к скорости света может отличаться от единицы не больше, чем на 3×10 −15 . Дмитрий Трунин
Пусть требуется найти с точностью до (с недостатком). Расположим вычисления так: Мы сначала находим приближенный корень с точностью до 1 только из целого числа 2. Получим 1 (и в остатке 1). Пишем в корне цифру 1 и ставим после нее запятую. Теперь находим цифру десятых. Для этого приписываем к остатку 1 цифры 3 и 5, стоящие направо от запятой, и продолжаем извлечение так, как будто мы извлекали корень из целого числа 235. Полученную цифру 5 пишем в корне на месте десятых. Остальные цифры подкоренного числа (104) нам не нужны. Что полученное число 1,5 будет действительно приближенным корнем с точностью до , видно из следующего; если бы мы находили наибольший целый корень из 235 с точностью до 1, то получили бы 15, значит, Разделив каждое из этих чисел на 100, получим: (От прибавления числа 0,00104 двойной знак ≤ должен измениться, очевидно, на знак <, а знак > остается (так как 0,00104 < 0,01).) Пусть требуется найти с точностью до приближенный с недостатком. Найдем целое число, потом - цифру десятых, затем и цифру сотых. Корень из целого числа будет 15 целых. Чтобы получить цифру десятых, надо, как мы видели, приписать к остатку 23 еще две цифры, стоящие направо от запятой: В нашем примере этих цифр нет вовсе; ставим на их место нули. Приписав их к остатку и продолжая действие так, как будто находим корень из целого числа 24800, мы найдем цифру десятых 7. Остается найти цифру сотых. Для этого приписываем к остатку 151 еще два нуля и продолжаем извлечение, как будто мы находим корень из целого числа 2480000. Получаем 15,74. Что это число действительно есть приближенный корень из 248 с точностью до с недостатком, видно из следующего. Если бы мы находили наибольший целый квадратный корень из целого числа 2480000, то получили бы 1574, значит, Разделив каждое из этих чисел на 10000 (1002), получим: 15,74 2 ≤ 248; 15,75 2 > 248. Значит, 15,74 есть та десятичная дробь, которую мы назвали приближенным корнем с недостатком с точностью до до 248. Правило
. Чтобы извлечь из данного целого числа или из данной десятичной дроби приближенный корень с недостатком с точностью до , до , до и т. д., находят сначала приближенный корень с недостатком с точностью до 1, извлекая корень из целого числа (если его нет, пишут в корне 0 целых).
Потом находят цифру десятых. Для этого к остатку приписывают две цифры покоренного числа, стоящие направо от запятой (если их нет, приписывают к остатку два нуля), и продолжают извлечение так, как это делается при извлечении корня из целого числа. Полученную цифру пишут в корне на месте десятых.
Затем находят цифру сотых. Для этого к остатку приписывают снова две цифры, стоящие направо от тех, которые были только что снесены, и т. д.
Таким образом, при извлечении корня из целого числа с десятичной дробью число надо делить на грани по две цифры в каждой, начиная от запятой, как влево (в целой части числа), так и вправо (в дробной части)
. Примеры.
В последнем примере мы обратили дробь в десятичную, вычислив восемь десятичных знаков, чтобы образовались четыре грани, потребные для нахождения четырех десятичных знаков корня. 9 сентября 2007 года пилот Логан Гомес одержал победу в гонке Chicagoland 100 чемпионата IRL Indy Pro Series. Обладателя второго места он опередил на 0,0005 секунды,
установив рекорд плотности финиша в мировом автоспорте. Какое оборудование позволяет измерять время с такой точностью? На волне маяка В современных гонках хронометраж ведется полностью автоматически. На каждый автомобиль устанавливается радиомаячок, излучающий радиоволны на уникальной частоте. Антенны, расположенные в строго определенных местах на треке, улавливают его сигнал и по частоте определяют, какой именно автомобиль проехал мимо. Антенны располагаются по две рядом: засекая время прохождения расстояния от одной антенны до другой, компьютер определяет скорость движения машины. На трассе может располагаться до 20 антенн. Особые антенны служат для контроля скорости на пит-лэйне. Информация с радиоприемников поступает в тайминг-центр, где более 20 инженеров непрерывно следят за работой компьютеров. На всякий случай система хронометража дублируется парой инфракрасных фотоэлементов, установленных на линии финиша Тим Скоренко
Именно в серии Indyсar требования к хронометражу самые строгие. Никакой другой чемпионат не может похвастаться измерением времени с точностью до десятитысячной доли секунды. Подавляющее количество серий ограничивается 0,001 с, и этого чаще всего хватает с запасом, но бывают и казусы: например, на квалификации Гран-при Европы 1997 года в классе «Формулы-1» аж три пилота умудрились показать время, совпадающее до тысячной доли секунды, — 1.21.072. Поул-позиция в итоге досталась Жаку Вильнёву, который проехал свой быстрый круг раньше других. В «Формуле-1» точность хронометража заметно изменялась с течением времени. В первом чемпионате 1950 года для полноценного учета финиша пилотов вполне хватало 0,1 с. Не было ни одной гонки, входящей в зачет чемпионата, где разрыв между пилотами был бы меньше секунды. Точность до 0,1 ведет свой отсчет с самого первого Гран-при в истории автогонок — Гран-при Франции 1906 года, где время победителя, Ференца Шиша на «Рено», составило 12 часов 14 минут и 7,4 секунды (не чета коротким и легким сегодняшним заездам, не так ли?). На большинстве же гонок, проведенных до Первой мировой войны, точность и вовсе не превышала 1 с. В Америке хронометристы были гораздо прогрессивнее. Послевоенные гонки серии AAA (в последствии — CART) требовали чаще всего точности измерения до 0,01. Это было связано в первую очередь с конфигурацией трасс и обилием овалов, где разрывы между гонщиками крайне малы. Невероятная точность хронометража современных IRL обусловлена тем же самым фактором: из семнадцати этапов чемпионата 2010 года на овалах проводится восемь. Хронометраж автогонок неразрывно связан с ведущими мировыми производителями часов и электроники: TAG Heuer, Tissot, Omega, Longines… Почти все они так или иначе представлены в различных видах спорта как официальные хронометристы. Ошибки и неточности в измерении времени сегодня практически исключены. С 1992 года и по сей день вышеупомянутое Гран-при Европы"97 стало единственным хронометрическим курьезом «Формулы-1», а в IRL даже такие казусы совершенно невозможны. Как ни странно, понятие «официальный хронометрист» появилось совсем недавно. Это сегодня компания Tissot «ведет» чемпионат мира по мотогонкам, и никакая другая компания не имеет права вмешиваться. Еще 30 лет назад на каждой отдельной гонке были свои хронометристы, «вооруженные» тем оборудованием, которое могли закупить организаторы. До Второй мировой практически во всех гоночных сериях и классах хронометраж проводился вручную: у трассы стояли специально обученные люди с секундомерами. Они фиксировали время прохождения круга очередной машиной и записывали данные. Впрочем, были и «прорывы». В 1911-м на первой гонке Indianapolis 500 инженер Чарли Уорнер сконструировал и добился применения первой в истории полуавтоматической системы хронометража. По линии старта-финиша была слабо натянута и чуть приподнята над кирпичным покрытием тонкая проволока. Каждая машина прижимала проволоку к земле, усиливая ее натяжение. К проволоке крепился молоточек-печать, который при натяжении ставил чернильную отметку на медленно ползущей ленте с делениями. Точность измерения достигала 0,01 с! Номера машин напротив каждой точки хронометрист ставил вручную. Система не прижилась по смешной причине: в середине гонки автомобиль гонщика Херба Литтла порвал проволоку. Пока натянули новую (бегая перед несущимися машинами), прошло не менее 20 кругов, в течение которых хронометраж велся приблизительно. Победа в гонке была присуждена Рэю Хэрроуну на Marmon, но другой известный гонщик, Ральф Малфорд, до самой смерти был уверен, что именно он выиграл первую в истории Indy 500. Расцвет успешного применения полуавтоматических систем приходится на 1930-е. В Indy 500 тогда использовали хронографы Stewart-Warner или огромные Loughborough-Hayes. В первые годы существования серии NASCAR хронометраж велся просто ужасно. В некоторых гонках на финише сидел человек с бумагой и карандашом и фиксировал: такой-то идет первым, такой-то — вторым. Правда, это касалось только гравийных и грязевых трасс. На автодромах дело обстояло получше. В частности, именно на гонке в Элхарт-Лейк"1951 применили хронограф Streeter-Amet. Прибор последовательно печатал (в десятых долях секунды) на бумажной ленте время каждого проносящегося мимо автомобиля, работа человека состояла в написании номеров машин напротив каждого числа. Полностью автоматическая система тайминга была впервые использована в гонке чемпионата USAC на трассе Онтарио в 1970 году. Каждый автомобиль был оборудован передатчиком, излучающим волны на своей собственной, уникальной частоте. На линии старта-финиша была установлена антенна, улавливающая частоту колебаний каждого трансмиттера, — остальную работу выполнял компьютер. Профессиональный хронометрист Дэвид Маккинни, работавший в 1960-х годах на различных гонках в Австралии и Новой Зеландии, дал нам интересную информацию: «Если самый квалифицированный хронометрист с самым лучшим хронометром сумеет точно ‘поймать" десятую долю секунды, то ему просто повезло». Поэтому все ручные измерения, которые когда-либо производились в гонках, можно смело считать приблизительными. В Европе автоматические системы появились намного позже, чем в Америке. В международных сериях вроде «Формулы-1» царили разброд и шатание. Вплоть до конца 1970-х на разных Гран-при хронометражем занимались совершенно разные люди, использовавшие различное оборудование и методы. На свободных заездах роль хронометристов чаще всего выполняли жены гонщиков. Например, Норма Хилл, жена двукратного чемпиона мира Грэма Хилла, ездила с мужем на каждый Гран-при и лично засекала его время на круге, перепроверяя работу маршалов. В середине 1970-х, устав от постоянной путаницы и ошибок, команда Ferrari начала возить на Гран-при собственное высокоточное оборудование, закупленное в Америке. Один из механиков извечного соперника Ferrari команды Lotus спросил у своего руководителя Колина Чепмена: «Почему мы не поступим так же?» «Вы на самом деле думаете, что от этого наши машины поедут быстрее?» — отвечал Чепмен. Этот ответ очень точно характеризует европейское отношение к точности хронометража в те годы. Впрочем, к концу 1970-х почти все крупные команды заключили договоры с производителями часов и возили с собой собственные тайминговые системы. После одного из заездов журнал Autosport писал: «Команды публикуют в официальных отчетах тайминг такой точности, что официальные цифры организаторов Гран-при выглядят как сделанные с помощью часов Микки-Мауса!» В связи с ошибками тайминга регулярно возникали замечательные инциденты. Например, во время дождевого Гран-при Канады 1973 года на трассу впервые был выведен сэйфти-кар. Хронометристы были сбиты столку, напутали с круговыми и неправильно сложили время до и после пейс-кара. В итоге победу последовательно праздновали Эмерсон Фиттипальди из Lotus, Джеки Оливер из Shadow и Петер Ревсон из МcLaren. Победа досталась последнему — после нескольких часов препирательств. Не менее занимательная история случилась на Гран-при Швеции 1975 года. Гонщик March Витторио Брамбилла был далеко не самым быстрым в пелатоне, но именно он завоевал в той гонке поул-позицию. Это произошло оттого, что конструктор March Робин Херд незаметно прошел прямо перед фотоэлементом регистрирующего прибора за полсекунды до того, как Брамбилла пересек финишную черту. Каким-то чудом никто этого не увидел, а прибор зафиксировал время пешего Херда, а вовсе не гонщика. Сегодняшние гонки суть торжество высоких технологий. К примеру, серия NASCAR чуть ли не последней переходила на современные методы хронометража, максимально придерживаясь традиций. Но сегодня системы тайминга NASCAR считаются одними из лучших в мире. Компания Tissot, официальный хронометрист заокеанской серии в течение последних четырех лет, оборудовала каждую трассу так, что европейские организаторы могут только позавидовать. В гонках, где из 36 этапов сезона 34 проходят на овалах, точность тайминга играет огромную роль. Не менее серьезные системы используются и в чемпионате мира по мотогонкам (его хронометристом также является компания Tissot). В отличие от NASCAR, тут не требуется сложных систем наблюдения, чтобы определить, кто же впереди: мотоциклисты идут не таким плотным пелатоном. Но поскольку трассы MotoGP традиционной европейской конфигурации, а не овалы, сложностей тоже хватает. Установка отсечек времени на определенных местах трассы требует тщательного продумывания (овалы попросту геометрически делятся на 4−8 частей). Сегодняшние компьютерные технологии практически исключают возможность ошибки хронометража в авто- или мотогонках. Организаторы Гран-при давно нашли себе на голову совершенно другие проблемы — безопасности, экологии и т. д. А фиксаторы времени работают себе и работают. Можно сказать, как часы.
Решение
. В разложении (1) заменяем х на -х 2 , получаем:
, -∞![]() .
.
Решение
. Имеем
Пользуясь формулой (4), можем записать:
подставляя вместо х в формулу –х, получим:
Отсюда находим: ln(1+x)-ln(1-x) = -
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а
). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х
стоит k(х-а
) m , где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t
=х-а
и раскладывать полученную функцию относительно t в ряд Маклорена.
Решение. Сначала найдем 1-x-6x 2 =(1-3x)(1+2x) , .
![]() на элементарные:
на элементарные:
с областью сходимости |x| < 1/3.
Решение
. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х
=3. Однако проще будет воспользоваться имеющимся разложением (5):
=
Полученный ряд сходится при или –3
Решение
.
Ряд сходится при , или -2 < x < 5.
Решение
. Сделаем замену t=х-2:
Воспользовавшись разложением (3), в котором на место х подставим π / 4 t, получим:
Полученный ряд сходится к заданной функции при -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Приближенные вычисления с помощью степенных рядов
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Рассмотрим разложение функции в степенной ряд:
Для того, чтобы вычислить приближенное значение функции в заданной точке х
, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n
членов (n
– конечное число), а остальные слагаемые отбрасывают:
Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r n (x) . Для этого применяют следующие приемы:
Решение
. Воспользуемся разложением , где x=1/2 (см. пример 5 в предыдущей теме):
Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
Таким образом, мы можем отбросить этот остаток и получаем
Решение
. Воспользуемся биномиальным рядом. Так как 5 3 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5 3 +5.

так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
, поэтому его и следующие за ним члены можно отбросить.
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Решение
. Соответствующий неопределенный интеграл не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx
на x
, получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим
 .
.
Решение
.

![]() . Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
. Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
≈0.0001<0.001. Следовательно,  .
.![]()

![]()



 В современных гонках хронометраж ведется полностью автоматически. На каждый автомобиль устанавливается радиомаячок, излучающий радиоволны на уникальной частоте. Антенны, расположенные в строго определенных местах на треке, улавливают его сигнал и по частоте определяют, какой именно автомобиль проехал мимо. Антенны располагаются по две рядом: засекая время прохождения расстояния от одной антенны до другой, компьютер определяет скорость движения машины. На трассе может располагаться до 20 антенн. Особые антенны служат для контроля скорости на пит-лэйне. Информация с радиоприемников поступает в тайминг-центр, где более 20 инженеров непрерывно следят за работой компьютеров. На всякий случай система хронометража дублируется парой инфракрасных фотоэлементов, установленных на линии финиша.
В современных гонках хронометраж ведется полностью автоматически. На каждый автомобиль устанавливается радиомаячок, излучающий радиоволны на уникальной частоте. Антенны, расположенные в строго определенных местах на треке, улавливают его сигнал и по частоте определяют, какой именно автомобиль проехал мимо. Антенны располагаются по две рядом: засекая время прохождения расстояния от одной антенны до другой, компьютер определяет скорость движения машины. На трассе может располагаться до 20 антенн. Особые антенны служат для контроля скорости на пит-лэйне. Информация с радиоприемников поступает в тайминг-центр, где более 20 инженеров непрерывно следят за работой компьютеров. На всякий случай система хронометража дублируется парой инфракрасных фотоэлементов, установленных на линии финиша.
Казусы и провалы
 Сегодня системы тайминга Indycar и NASCAR считаются одними из лучших в мире. Каждая трасса оборудована так, что европейские организаторы могут только позавидовать. Счет идет на 0,0001 секунды (для Indycar), а зрители в прямом эфире в любой момент могут получить информацию о скорости каждой машины на треке, ее времени на круге и любом из секторов круга, разрывы в пелатоне с точностью до сектора и т. д. — в общем, максимальную информацию. В гонках, где половина этапов сезона проходит на овалах, точность тайминга играет огромную роль. Победитель частенько определяется посредством фотофиниша.
Сегодня системы тайминга Indycar и NASCAR считаются одними из лучших в мире. Каждая трасса оборудована так, что европейские организаторы могут только позавидовать. Счет идет на 0,0001 секунды (для Indycar), а зрители в прямом эфире в любой момент могут получить информацию о скорости каждой машины на треке, ее времени на круге и любом из секторов круга, разрывы в пелатоне с точностью до сектора и т. д. — в общем, максимальную информацию. В гонках, где половина этапов сезона проходит на овалах, точность тайминга играет огромную роль. Победитель частенько определяется посредством фотофиниша.


«Формула-1»


Торжество технологий

 Система воинских званий в российской императорской армии
Система воинских званий в российской императорской армии Самая маленькая армия в мире Вооруженные силы Турции
Самая маленькая армия в мире Вооруженные силы Турции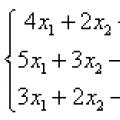 Метода гаусса: примеры решения слау
Метода гаусса: примеры решения слау