График функции у равен корень из х. Функции вида y = √x, их свойства и графики — Гипермаркет знаний
N-й степени из действительного числа, отметили, что из любого неотрицательного числа можно извлечь корень любой степени (второй, третьей, четвертой и т.д.), а из отрицательного числа можно извлечь корень любой нечетной степени. Но тогда следует подумать и о функции вида , о ее графике, о ее свойствах. Этим мы и займемся в нас стоящем параграфе. Сначала поговорим о функции в случае неотрицательных значений аргумента .
Начнем с известного вам случая, когда n =2, т.е. с функции На рис. 166 изображен график функции и график функции у = х 2 , х>0. Оба графика представляют собой одну и ту же кривую - ветвь параболы, только по-разному расположенную на координатной плоскости. Уточним: эти графики симметричны относительно прямой у = х, поскольку состоят из точек, симметричных друг другу относительно указанной прямой. Смотрите: на рассматриваемой ветви параболы у = х 2 есть точки (0; 0), (1; 1), (2; 4), (3; 9), (4; 16), а на графике функции точки (0; 0), (1; 1), (4; 2), (9; 3), (16; 4).
Точки (2; 4) и (4; 2), (3; 9) и (9; 3), (4; 16) и (16; 4) симметричны относительно прямой у = х, (а точки (0; 0) и (1; 1) лежат на этой прямой). И вообще, для любой точки (а; а 2) на графике функции у = х 2 есть симметричная ей относительно прямой у = x точка (а 2 ; а) на графике функции и обратно. Справедлива следующая теорема.

Доказательство.
Будем считать для определенности, что а и b - положительные числа. Рассмотрим треугольники ОАМ и ОВР (рис. 167). Они равны, значит, ОР = ОМ и ![]() . Но тогда и
. Но тогда и ![]() поскольку прямая у = х - биссектриса угла АОВ. Итак, треугольник РОМ - равнобедренный, ОН - его биссектриса, а значит, и ось симметрии. Точки М и Р симметричны относительно прямой ОН, что и требовалось доказать.
поскольку прямая у = х - биссектриса угла АОВ. Итак, треугольник РОМ - равнобедренный, ОН - его биссектриса, а значит, и ось симметрии. Точки М и Р симметричны относительно прямой ОН, что и требовалось доказать.
Итак, график функции можно получить из графика функции у = х 2 , х>0 с помощью преобразования симметрии относительно прямой у = х. Аналогично график функции можно получить из графика функции у = х 3 , х> 0 с помощью преобразования симметрии относительно прямой у=х; график функции можно получить из графика функции с помощью преобразования симметрии относительно прямой у = х и т.д. Напомним, что график функции напоминает по виду ветвь параболы Чем больше п, тем круче эта ветвь устремляется вверх на промежутке и тем ближе подходит к оси х в окрестности точки х=0 (рис. 168).

Сформулируем общий вывод: график функции симметричен графику функции , относительно прямой у = х(рис. 169).
Свойства функции
1)
2) функция не является ни четной, ни нечетной;
3) возрастает на
4) не ограничена сверху, ограничена снизу;
5) не имеет наибольшего значения;
6) непрерывна;
7)
Обратите внимание на одно любопытное обстоятельство. Рассмотрим две функции, графики которых изображены на рис. 169: Только что мы перечислили семь свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Но, уточним, пока одинаковы.
Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково, и ввели понятия выпуклости вверх и выпуклости вниз. График функции обращен выпуклостью вверх, тогда как график функции у = х п обращен выпуклостью вниз.

Обычно говорят, что непрерывная функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 170); непрерывная функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка (рис. 171).
Свойство выпуклости мы будем в дальнейшем включать в процедуру чтения графика. Отметим его"(продолжив нумерацию описанных ранее свойств) для рассматриваемой функции:
8) функция выпукла вверх на луче
В предыдущей главе мы познакомились еще с одним свойством функции - дифференцируемостью, видели, что функция у = х п дифференцируема в любой точке, ее производная равна пх n-1 . Геометрически это означает, что в любой точке графика функции у = х п к нему можно провести касательную. Этим же свойством обладает и график функции : в любой его точке к графику можно провести касательную. Таким образом, мы можем отметить еще одно свойство функции
9) функция дифференцируема в любой точке х > 0.
Обратите внимание: о дифференцируемости функции в точке х = 0 речь не идет - в этой точке касательная к графику функции совпадает с осью у, т.е. перпендикулярна оси абсцисс.
Пример 1. Построить график функции
Решение.
1)Перейдем к вспомогательной системе координат с началом в точке (-1; -4) - пунктирные прямые х = -1 и у = -4 на рис. 172.
2) «Привяжем» функцию к новой системе координат. Это и будет требуемый график.
Пример 2.
Решить уравнение
Решение. Первый способ.
1) Введем в рассмотрение две функции
2) Построим график функции

3) Построим график линейной функции у=2-х (см. рис. 173).
4) Построенные графики пересекаются в одной точке А, причем по графику можно сделать предположение, что координаты точкиА таковы: (1; 1). Проверка показывает, что на самом деле точка (1; 1) принадлежит и графику функции , и графику функции у=2-x. Значит, наше уравнение имеет один корень: х = 1 - абсцисса точки А.
Второй способ.
Геометрическая модель, представленная на рис. 173, наглядно иллюстрирует следующее утверждение, которое иногда позволяет очень изящно решить уравнение (и которым мы уже воспользовались в § 35 при решении примера 2):
Если функция у=f(х) возрастает, а функция у=g(х) убывает и если уравнение f(х)=g(х) имеет корень, то он только один.
Вот как, опираясь на это утверждение, мы можем решить заданное уравнение:
1) заметим, что при х = 1 выполняется равенство , значит, х = 1 - корень уравнения (этот корень мы угадали);
2) функция y=2-x убывает, а функция возрастает; значит, корень у заданного уравнения только один, и этим корнем является найденное выше значение x = 1.
Ответ : x = 1.
До сих пор мы говорили о функции только для неотрицательных значений аргумента. Но ведь если п - нечетное число, выражение имеет смысл и для x <0. Значит, есть смысл поговорить о функции в случае нечетного п для любых значений х.
Собственно говоря, к перечисленным добавится только одно свойство:
если n - нечетное число (n = 3,5, 7,...), то - нечетная функция.
В самом деле, пусть для нечетного показателя n такие преобразования верны. Итак, f(-x) = -f(x), а это и означает нечетность функции.
Как же выглядит график функции в случае нечетного показателя n? При так, как показано на рис. 169, - это ветвь искомого графика. Добавив к ней ветвь, симметричную ей относительно начала координат (что, напомним, характерно для любой нечетной функции), получим график функции (рис. 174). Обратите внимание: ось у является касательной к графику в точке х = 0.
Итак, повторим еще раз:
если п - четное число, то график функции имеет вид, представленный на рис. 169;
если п - нечетное число, то график функции имеет вид, представленный на рис. 174.

Пример 3.
Построить и прочитать график функции у = f(x), где 
Решение.
Сначала построим график функции и выделим его часть на луче (рис. 175).
Затем построим график функции и выделим его часть на открытом луче (рис. 176). Наконец, оба «кусочка» изобразим в одной системе координат - это и будет график функции у = f(x)(рис. 177).
Перечислим (опираясь на построенный график) свойства функции у = f(x):
1)
2) ни четна, ни нечетна;
3) убывает на луче , возрастает на луче
4) не ограничена снизу, ограничена сверху;
5) нет наименьшего значения, а (достигается в точке х = 1);
6) непрерывна;
7)
8) выпукла вниз при , выпукла вверх на отрезке , выпукла вниз при
9) функция дифференцируема всюду, кроме точек х = 0 и х = 1.
10) график функции имеет горизонтальную асимптоту это означает, напомним, что
Пример 4. Найти область определения функции:
![]()
Решение,
а) Под знаком корня четной степени должно находиться неотрицательное число, значит, задача сводится к решению неравенства
б) Под знаком корня нечетной степени может находиться любое число, значит, здесь на х не накладывается никаких ограничений, т.е. D(f) = R.
в) Выражение имеет смысл при условии а выражение Значит, должны одновременно выполняться два неравенства: ![]() т.е. задача сводится к решению системы неравенств:
т.е. задача сводится к решению системы неравенств:
Решая неравенство
Решим неравенство Разложим левую часть неравенства на множители: Левая часть неравенства обращается в 0 в точках -4 и 4. Отметим эти точки на числовой прямой (рис. 178). Числовая прямая разбивается указанными точками на три промежутка, причем на каждом промежутке выражение р(х)=(4-х)(4 + х) сохраняет постоянный знак (знаки указаны на рис. 178). Промежуток, на котором выполняется неравенство р(х)>0, заштрихован на рис. 178. По условию задачи нас интересуют и те точки х, в которых выполняется равенство р(х) = 0. Таких точек две: х =-4, х =4 - они отмечены на рис. 178 темными кружочками. Таким образом, на рис. 178 представлена геометрическая модель решения второго неравенства системы.

Отметим найденные решения первого и второго неравенств системы на одной координатной прямой, использовав для первого - верхнюю, а для второго - нижнюю штриховку (рис. 179). Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали. Таким промежутком является отрезок [-1, 4].
Ответ. D(f) = [-1,4].
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн , Математика в школе
Основные цели:
1) сформировать представление о целесообразности обобщённого исследования зависимостей реальных величин на примере величин, связанных отношением у=
2) формировать способность к построению графика у= и его свойства;
3) повторить и закрепить приёмы устных и письменных вычислений, возведение в квадрат, извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:

2. Образец для выполнения задания в группах:

3. Образец для самопроверки самостоятельной работы:

4. Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной работе.
4) Я допустил ошибки в самостоятельной работе (перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали множество действительных чисел, действия с ними, построили алгоритм для описания свойств функции, повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством действительных чисел, функцией.
2. Актуализация знаний и фиксация затруднений в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x 2 , y = - x 2 ,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний.
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать зависимости между величинами? (С помощью текста, формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между двумя величинами, где каждому значению одной переменной соответствует единственное значение другой переменной y = f(x)).
Как называется х? (Независимая переменная - аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c, y =x 2 , y = - x 2 , ).
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x 2 , y = ?
3. Выявление причин затруднений и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость задана формулой y = с которой мы еще не встречались).
– Какая цель урока? (Познакомиться с функцией y = , ее свойствами и графиком. Функцией в таблице определять вид зависимости, строить формулу и график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и график).
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам, предложив группам построить график y = , затем проанализировать получившиеся результаты. Также группам можно предложить по алгоритму описать свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
Организация учебного процесса на этапе 5:
Постройте график у= - и опишите его свойства.

Свойства у= - .
1.Область определения функции.
2.Область значений функции.
3. y = 0, y> 0, y<0.
y =0, если x = 0.
y<0, если х(0;+)
4.Возрастания, убывания функции.
Функция убывает при х .
Построим график у=.

Выделим его часть на отрезке . Заметим, что у наим. = 1 при х = 1, а у наиб. =3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.
Построим график у=.
С помощью графика найдите наименьшее и наибольшее значения функции на отрезке .

7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки использования нового содержания совместно с ранее изученным: 2) повторить учебное содержание, которое потребуется на следующих уроках.
Организация учебного процесса на этапе 7:
Решите графически уравнение: = х – 6.

Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Ребята, какая цель стояла сегодня перед нами? (Изучить функцию у=, ее свойства и график).
– Какие знания нам помогли в достижении цели? (Умение искать закономерности, умение читать графики.)
– Проанализируйте свою деятельность на уроке. (Карточки с рефлексией)
Домашнее задание
п. 13 (до примера 2) № 13.3, 13.4
Решите графически уравнение.
Приведены основные свойства степенной функции, включая формулы и свойства корней. Представлены производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел степенной функции.
СодержаниеСтепенная функция, y = x p
,
с показателем p
имеет следующие свойства:
(1.1)
определена и непрерывна на множестве
при ,
при ;
(1.2)
имеет множество значений
при ,
при ;
(1.3)
строго возрастает при ,
строго убывает при ;
(1.4)
при ;
при ;
(1.5)
;
(1.5*)
;
(1.6)
;
(1.7)
;
(1.7*)
;
(1.8)
;
(1.9)
.
Доказательство свойств приводится на странице «Степенная функция (доказательство непрерывности и свойств) »
Корни - определение, формулы, свойства
Корень из числа x степени n - это число , возведение которого в степень n дает x :.
Здесь n = 2, 3, 4, ... - натуральное число, большее единицы.
Также можно сказать, что корень из числа x
степени n
- это корень (то есть решение) уравнения
.
Заметим, что функция является обратной к функции .
Квадратный корень из числа x
- это корень степени 2: .
Кубический корень из числа x
- это корень степени 3: .
Четная степень
Для четных степеней n = 2
m
,
корень определен при x ≥ 0
.
Часто используется формула, справедливая как для положительных, так и для отрицательных x
:
.
Для квадратного корня:
.
Здесь важен порядок, в котором выполняются операции - то есть сначала производится возведение в квадрат, в результате чего получается неотрицательное число, а затем из него извлекается корень (из неотрицательного числа можно извлекать квадратный корень). Если бы мы изменили порядок: , то при отрицательных x корень был бы не определен, а вместе с ним не определено и все выражение.
Нечетная степень
Для нечетных степеней ,
корень определен для всех x
:
;
.
Свойства и формулы корней
Корень из x
является степенной функцией:
.
При x ≥ 0
имеют место следующие формулы:
;
;
,
;
.
Эти формулы также могут быть применимы и при отрицательных значениях переменных . Нужно только следить за тем, чтобы подкоренное выражение четных степеней не было отрицательным.
Частные значения
Корень 0 равен 0: .
Корень 1 равен 1: .
Квадратный корень 0 равен 0: .
Квадратный корень 1 равен 1: .
Пример. Корень из корней
Рассмотрим пример квадратного корня из корней:
.
Преобразуем внутренний квадратный корень, применяя приведенные выше формулы:
.
Теперь преобразуем исходный корень:
.
Итак,
.

y = x p при различных значениях показателя p .
Здесь приводятся графики функции при неотрицательных значениях аргумента x . Графики степенной функции, определенной при отрицательных значениях x , приводятся на странице «Степенная функция, ее свойства и графики »
Обратная функция
Обратной для степенной функции с показателем p является степенная функция с показателем 1/p .
Если ,
то .
Производная степенной функции
Производная n-го порядка:
;
Вывод формул > > >
Интеграл от степенной функции
P ≠ - 1
;
.
Разложение в степенной ряд
При - 1
< x < 1
имеет место следующее разложение:
Выражения через комплексные числа
Рассмотрим функцию комплексного переменного z
:
f(z)
= z t
.
Выразим комплексную переменную z
через модуль r
и аргумент φ
(r = |z|
):
z = r e i φ
.
Комплексное число t
представим в виде действительной и мнимой частей:
t = p + i q
.
Имеем:
Далее учтем, что аргумент φ
определен не однозначно:
,
Рассмотрим случай, когда q = 0
,
то есть показатель степени - действительное число, t = p
.
Тогда
.
Если p
- целое, то и kp
- целое. Тогда, в силу периодичности тригонометрических функций:
.
То есть показательная функция при целом показателе степени, для заданного z
,
имеет только одно значение и поэтому является однозначной.
Если p - иррациональное, то произведения kp ни при каком k не дают целого числа. Поскольку k пробегает бесконечный ряд значений k = 0, ±1, ±2, ±3, ... , то функция z p имеет бесконечно много значений. Всякий раз, когда аргумент z получает приращение 2 π (один оборот), мы переходим на новую ветвь функции.
Если p
- рациональное, то его можно представить в виде:
,
где m, n
- целые, не содержащие общих делителей. Тогда
.
Первые n
величин, при k = k 0
= 0, 1, 2, ... n-1
,
дают n
различных значений kp
:
.
Однако последующие величины дают значения, отличающиеся от предыдущих на целое число. Например, при k = k 0
+ n
имеем:
.
Тригонометрические функции, аргументы которых различаются на величины, кратные 2
π
,
имеют равные значения. Поэтому при дальнейшем увеличении k
мы получаем те же значения z p
,
что и для k = k 0
= 0, 1, 2, ... n-1
.
Таким образом, показательная функция с рациональным показателем степени является многозначной и имеет n значений (ветвей). Всякий раз, когда аргумент z получает приращение 2 π (один оборот), мы переходим на новую ветвь функции. Через n таких оборотов мы возвращаемся на первую ветвь, с которой начинался отсчет.
В частности, корень степени n
имеет n
значений. В качестве примера рассмотрим корень n
- й степени действительного положительного числа z = x
.
В этом случае φ 0 = 0
, z = r = |z| = x
,
.
.
Так, для квадратного корня, n = 2
,
.
Для четных k, (- 1
)
k = 1
.
Для нечетных k, (- 1
)
k = - 1
.
То есть квадратный корень имеет два значения: + и - .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
 Система воинских званий в российской императорской армии
Система воинских званий в российской императорской армии Самая маленькая армия в мире Вооруженные силы Турции
Самая маленькая армия в мире Вооруженные силы Турции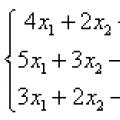 Метода гаусса: примеры решения слау
Метода гаусса: примеры решения слау