Si të kërkoni asimptota të një funksioni. Si të gjejmë asimptotat e grafikut të një funksioni? çfarë do të thotë
Sa asimptota mund të ketë grafiku i një funksioni?
Jo një, një, dy, tre, ... ose pafundësisht shumë. Nuk do të shkojmë larg për shembuj, le të kujtojmë funksionet elementare. Një parabolë, një parabolë kubike dhe një valë sinusale nuk kanë fare asimptota. Grafiku i një funksioni logaritmik eksponencial ka një asimptotë të vetme. Arktangjentja dhe arkotangjentja kanë dy prej tyre, dhe tangjentja dhe kotangjentja kanë pafundësisht shumë. Nuk është e pazakontë që një grafik të ketë asimptota horizontale dhe vertikale. Hiperbola, do të të dua gjithmonë.
Çfarë do të thotë të gjesh asimptotat e grafikut të një funksioni?
Kjo do të thotë të zbuloni ekuacionet e tyre dhe të vizatoni vija të drejta nëse e kërkon problemi. Procesi përfshin gjetjen e kufijve të një funksioni.
Asimptotat vertikale të grafikut të një funksioni
Asimptota vertikale e grafikut, si rregull, ndodhet në pikën e ndërprerjes së pafundme të funksionit. Është e thjeshtë: nëse në një pikë funksioni pëson një ndërprerje të pafundme, atëherë vija e drejtë e specifikuar nga ekuacioni është asimptota vertikale e grafikut.
Shënim: Ju lutemi vini re se hyrja përdoret për t'iu referuar dy koncepteve krejtësisht të ndryshme. Nëse një pikë nënkuptohet ose një ekuacion i një linje varet nga konteksti.
Kështu, për të përcaktuar praninë e një asimptote vertikale në një pikë, mjafton të tregohet se të paktën një nga kufijtë e njëanshëm është i pafund. Më shpesh kjo është pika ku emëruesi i funksionit është zero. Në thelb, ne kemi gjetur tashmë asimptota vertikale në shembujt e fundit të mësimit mbi vazhdimësinë e një funksioni. Por në disa raste ekziston vetëm një kufi i njëanshëm, dhe nëse është i pafund, atëherë përsëri - dashuroni dhe favorizoni asimptotën vertikale. Ilustrimi më i thjeshtë: dhe boshti i ordinatave.
Nga sa më sipër, rrjedh edhe një fakt i dukshëm: nëse funksioni është i vazhdueshëm, atëherë nuk ka asimptota vertikale. Për disa arsye më erdhi në mendje një parabolë. Vërtet, ku mund të "ngjisni" një vijë të drejtë këtu? ...po... e kuptoj... Ndjekësit e xhaxha Frojdit u bënë histerikë =)
Deklarata e kundërt është përgjithësisht e rreme: për shembull, funksioni nuk përcaktohet në të gjithë vijën numerike, por është plotësisht i privuar nga asimptota.
Asimptotat e pjerrëta të grafikut të një funksioni
Asimptotat e zhdrejta (si rast i veçantë - horizontale) mund të nxirren nëse argumenti i funksionit priret në "plus infinity" ose në "minus infinity". Prandaj, grafiku i një funksioni nuk mund të ketë më shumë se 2 asimptota të prirura. Për shembull, grafiku i një funksioni eksponencial ka një asimptotë të vetme horizontale në, dhe grafiku i arktangjentës at ka dy asimptota të tilla, dhe në atë të ndryshme.
Kur grafiku në të dy vendet i afrohet një asimptote të vetme të zhdrejtë, atëherë është zakon të kombinohen "pafundësitë" nën një hyrje të vetme. Për shembull, ...e keni marrë me mend saktë: .
Asimptota e grafikut të një funksioni y = f(x) është një drejtëz që ka vetinë që distanca nga pika (x, f(x)) në këtë drejtëz të priret në zero ndërsa pika e grafikut lëviz pafundësisht nga origjina.
Në figurën 3.10. jepen shembuj grafikë vertikale, horizontale Dhe të prirur asimptotë.
Gjetja e asimptotave të grafikut bazohet në tre teoremat e mëposhtme.
Teorema e asimptotës vertikale. Le të përcaktohet funksioni y = f(x) në ndonjë fqinjësi të pikës x 0 (duke përjashtuar, ndoshta, vetë këtë pikë) dhe të paktën një nga kufijtë e njëanshëm të funksionit është i barabartë me pafundësinë, d.m.th. Atëherë drejtëza x = x 0 është asimptota vertikale e grafikut të funksionit y = f(x).
Natyrisht, drejtëza x = x 0 nuk mund të jetë një asimptotë vertikale nëse funksioni është i vazhdueshëm në pikën x 0, pasi në këtë rast ![]() . Rrjedhimisht, asimptotat vertikale duhet të kërkohen në pikat e ndërprerjes së funksionit ose në skajet e domenit të tij të përkufizimit.
. Rrjedhimisht, asimptotat vertikale duhet të kërkohen në pikat e ndërprerjes së funksionit ose në skajet e domenit të tij të përkufizimit.
Teorema e asimptotës horizontale. Le të përcaktohet funksioni y = f(x) për x mjaftueshëm të madh dhe ka një kufi të kufizuar të funksionit. Atëherë drejtëza y = b është asimptota horizontale e grafikut të funksionit.
Komentoni. Nëse vetëm një nga kufijtë është i kufizuar, atëherë funksioni ka, në përputhje me rrethanat, mëngjarash ose me anën e djathtë asimptotë horizontale.
Në rast se , funksioni mund të ketë një asimptotë të zhdrejtë.
Teorema e asimptotës së zhdrejtë. Le të përcaktohet funksioni y = f(x) për x mjaftueshëm të madh dhe të ketë kufij të fundëm ![]() . Atëherë drejtëza y = kx + b është asimptota e pjerrët e grafikut të funksionit.
. Atëherë drejtëza y = kx + b është asimptota e pjerrët e grafikut të funksionit.
Asnjë provë.
Një asimptotë e zhdrejtë, ashtu si ajo horizontale, mund të jetë e djathtë ose e majtë nëse baza e kufijve përkatës përmban pafundësi të një shenje të caktuar.
Studimi i funksioneve dhe ndërtimi i grafikëve të tyre zakonisht përfshin hapat e mëposhtëm:
1. Gjeni domenin e përkufizimit të funksionit.
2. Shqyrtoni funksionin për çift-teksinë.
3. Gjeni asimptota vertikale duke ekzaminuar pikat e ndërprerjes dhe sjelljen e funksionit në kufijtë e fushës së përkufizimit, nëse ato janë të fundme.
4. Gjeni asimptota horizontale ose të zhdrejta duke shqyrtuar sjelljen e funksionit në pafundësi.
5. Gjeni ekstremet dhe intervalet e monotonitetit të funksionit.
6. Gjeni intervalet e konveksitetit të funksionit dhe pikave të lakimit.
7. Gjeni pikat e kryqëzimit me boshtet e koordinatave dhe, mundësisht, disa pika shtesë që qartësojnë grafikun.
Diferenciali i funksionit
Mund të vërtetohet se nëse një funksion ka një kufi të barabartë me një numër të fundëm për një bazë të caktuar, atëherë ai mund të përfaqësohet si shuma e këtij numri dhe një vlerë infiniteminale për të njëjtën bazë (dhe anasjelltas): .
Le ta zbatojmë këtë teoremë për një funksion të diferencueshëm: .
Kështu, rritja e funksionit Dу përbëhet nga dy terma: 1) linear në lidhje me Dx, d.m.th. f `(x)Dх; 2) jolineare në lidhje me Dx, d.m.th. a(Dx)Dх. Në të njëjtën kohë, që nga ![]() , ky term i dytë përfaqëson një pafundësi më shumë rendit të lartë se Dx (pasi Dx tenton në zero, priret në zero edhe më shpejt).
, ky term i dytë përfaqëson një pafundësi më shumë rendit të lartë se Dx (pasi Dx tenton në zero, priret në zero edhe më shpejt).
Diferenciale funksioni është pjesa kryesore, lineare në lidhje me Dx e rritjes së funksionit, e barabartë me produktin e derivatit dhe rritjen e ndryshores së pavarur dy = f `(x)Dx.
Le të gjejmë diferencialin e funksionit y = x.
Meqë dy = f `(x)Dх = x`Dх = Dх, atëherë dx = Dх, d.m.th. diferenciali i një ndryshoreje të pavarur është i barabartë me rritjen e kësaj ndryshoreje.
Prandaj, formula për diferencialin e një funksioni mund të shkruhet si dy = f `(x)dх. Kjo është arsyeja pse një nga shënimet për derivatin është thyesa dy/dx.

Kuptimi gjeometrik diferencial i ilustruar
Figura 3.11. Le të marrim një pikë arbitrare M(x, y) në grafikun e funksionit y = f(x). Le t'i japim argumentit x shtimin Dx. Atëherë funksioni y = f(x) do të marrë inkrementin Dy = f(x + Dх) - f(x). Le të vizatojmë një tangjente me grafikun e funksionit në pikën M, e cila formon një kënd a me drejtimin pozitiv të boshtit të abshisës, d.m.th. f `(x) = tan a. Nga trekëndësh kënddrejtë MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.
Kështu, diferenciali i një funksioni është rritja në ordinatën e tangjentes së tërhequr në grafikun e funksionit në një pikë të caktuar kur x merr shtimin Dx.
Vetitë e një diferenciali janë në thelb të njëjta me ato të një derivati:
3. d(u ± v) = du ± dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du - u dv)/v 2.
Megjithatë, ekziston pronë e rëndësishme diferenciali i një funksioni që derivati i tij nuk e zotëron është pandryshueshmëria e formës diferenciale.
Nga përkufizimi i diferencialit për funksionin y = f(x), diferenciali dy = f `(x)dх. Nëse ky funksion y është kompleks, d.m.th. y = f(u), ku u = j(x), pastaj y = f dhe f `(x) = f `(u)*u`. Atëherë dy = f `(u)*u`dх. Por për funksionin
u = j(x) diferencial du = u`dх. Prandaj dy = f `(u)*du.
Duke krahasuar barazitë dy = f `(x)dх dhe dy = f `(u)*du, sigurohemi që formula diferenciale të mos ndryshojë nëse në vend të një funksioni të ndryshores së pavarur x konsiderojmë një funksion të ndryshorja e varur u. Kjo veti e një diferenciali quhet pandryshueshmëri (d.m.th., pandryshueshmëri) e formës (ose formulës) të diferencialit.
Megjithatë, ka ende një ndryshim në këto dy formula: në të parën prej tyre, diferenciali i ndryshores së pavarur është i barabartë me rritjen e kësaj ndryshore, d.m.th. dx = Dx, dhe së dyti, diferenciali i funksionit du është vetëm pjesa lineare e rritjes së këtij funksioni Du dhe vetëm për Dх du » Du të vogla.
Do të ketë edhe detyra për vendim i pavarur, për të cilat mund të shihni përgjigjet.
Koncepti i asimptotës
Nëse fillimisht ndërtoni asimptotat e kurbës, atëherë në shumë raste ndërtimi i një grafiku të funksionit bëhet më i lehtë.
Fati i asimptotës është plot tragjedi. Imagjinoni se si është: gjithë jetën tuaj duke ecur në një vijë të drejtë drejt qëllimit tuaj të dashur, duke iu afruar sa më shumë që të jetë e mundur, por duke mos e arritur kurrë. Për shembull, përpiquni të lidhni tuajin rrugën e jetës me rrugën e personit të dëshiruar, në një moment afrohu thuajse afër, por as nuk e prek. Ose përpiquni të fitoni një miliard, por përpara se të arrini këtë qëllim dhe të hyni në Librin e Rekordeve Guinness për rastin tuaj, mungojnë të qindtat e një centi. Dhe të ngjashme. Kështu është me një asimptotë: ai vazhdimisht përpiqet të arrijë kurbën e grafikut të funksionit, i afrohet asaj në distancën minimale të mundshme, por nuk e prek kurrë.
Përkufizimi 1. Asimptotat janë ato vija të drejta të cilave grafiku i një funksioni afrohet në mënyrë arbitrare nga afër kur ndryshorja tenton në plus pafundësi ose minus pafundësi.
Përkufizimi 2. Drejtëza quhet asimptotë e grafikut të një funksioni nëse distanca nga pika e ndryshueshme M grafiku i funksionit deri në këtë vijë priret në zero ndërsa pika largohet pafundësisht M nga origjina përgjatë çdo dege të grafikut të funksionit.
Ekzistojnë tre lloje asimptotesh: vertikale, horizontale dhe të zhdrejtë.
Asimptota vertikale
Gjëja e parë që duhet të dini për asimptotat vertikale është se ato janë paralele me boshtin Oy .
Përkufizimi. Drejt x = aështë asimptota vertikale e grafikut të funksionit , nëse pika x = aështë pika e ndërprerjes së llojit të dytë për këtë funksion.
Nga përkufizimi del se drejtëza x = aështë asimptota vertikale e grafikut të funksionit f(x) nëse plotësohet të paktën një nga kushtet:
Në këtë rast, funksioni f(x) mund të mos përcaktohet fare, përkatësisht kur x ≥ a Dhe x ≤ a .
Koment:

Shembulli 1. Grafiku i një funksioni y=n x ka një asimptotë vertikale x= 0 (d.m.th. që përkon me boshtin Oy) në kufirin e fushës së përkufizimit, pasi kufiri i funksionit kur x tenton në zero nga e djathta është i barabartë me minus pafundësinë:
(foto lart).
veten dhe pastaj shikoni zgjidhjet
Shembulli 2. Gjeni asimptotat e grafikut të funksionit.
Shembulli 3. Gjeni asimptota të grafikut të një funksioni
Asimptota horizontale
Gjëja e parë që duhet të dini për asimptotat horizontale është se ato janë paralele me boshtin kau .
Nëse (kufiri i një funksioni pasi argumenti tenton në plus ose minus pafundësi është i barabartë me një vlerë të caktuar b), Kjo y = b – asimptotë horizontale i shtrembër y = f(x ) (djathtas kur X tenton në plus pafundësi, majtas kur X tenton në minus pafundësi dhe me dy anë nëse kufijtë si X priret në plus ose minus pafundësi janë të barabartë).

Shembulli 5. Grafiku i një funksioni
në a> 1 ka lënë asimpotote horizontale y= 0 (d.m.th. që përkon me boshtin kau), meqenëse kufiri i funksionit si "x" tenton në minus pafundësi është zero:
Kurba nuk ka një asimptotë horizontale të drejtë, pasi kufiri i funksionit si "x" tenton në plus pafundësi është i barabartë me pafundësinë:
Asimptota të zhdrejta
Asimptotat vertikale dhe horizontale që shqyrtuam më sipër janë paralele me boshtet e koordinatave, kështu që për t'i ndërtuar ato na duhej vetëm një numër i caktuar - pika në abshisë ose boshti i ordinatës nëpër të cilën kalon asimptota. Për një asimptotë të zhdrejtë, nevojitet një pjerrësi më e madhe k, e cila tregon këndin e prirjes së drejtëzës dhe termin e lirë b, e cila tregon se sa është vija mbi ose nën origjinën. Ata që nuk e kanë harruar gjeometrinë analitike dhe prej saj ekuacionet e drejtëzës, do të vërejnë se për asimptotën e zhdrejtë gjejnë ekuacioni i një drejtëze me pjerrësi. Ekzistenca e një asimptote të zhdrejtë përcaktohet nga teorema e mëposhtme, në bazë të së cilës gjenden koeficientët e sapopërmendur.
Teorema. Për të bërë kurbën y = f(x) kishte një asimptotë y = kx + b , është e nevojshme dhe e mjaftueshme që të ketë kufij të fundëm k Dhe b të funksionit në shqyrtim si variabli prirje x në plus pafundësi dhe minus pafundësi:
![]() (1)
(1)
![]() (2)
(2)
Numrat e gjetur në këtë mënyrë k Dhe b dhe janë koeficientët e asimptotës së zhdrejtë.
Në rastin e parë (pasi x tenton në plus pafundësi), fitohet një asimptotë e prirur djathtas, në rastin e dytë (pasi x tenton në minus pafundësi), fitohet një asimptotë e zhdrejtë majtas. Asimptota e zhdrejtë e djathtë është paraqitur në Fig. më poshtë.

Gjatë gjetjes së ekuacionit për asimptotën e zhdrejtë, është e nevojshme të merret parasysh tendenca e X në plus pafundësi dhe minus pafundësi. Për disa funksione, për shembull, ato racionale të pjesshme, këto kufij përkojnë, por për shumë funksione këto kufij janë të ndryshëm dhe vetëm njëri prej tyre mund të ekzistojë.
Nëse kufijtë përkojnë dhe x tenton në plus pafundësi dhe minus pafundësi, vija e drejtë y = kx + b është asimptota e dyanshme e lakores.
Nëse të paktën një nga kufijtë që përcaktojnë asimptotën y = kx + b , nuk ekziston, atëherë grafiku i funksionit nuk ka asimptotë të zhdrejtë (por mund të ketë një vertikale).
Është e lehtë të shihet se asimptota horizontale y = bështë rast i veçantë i zhdrejtë y = kx + b në k = 0 .
Prandaj, nëse në ndonjë drejtim një kurbë ka një asimptotë horizontale, atëherë në këtë drejtim nuk ka një të prirur dhe anasjelltas.
Shembulli 6. Gjeni asimptota të grafikut të një funksioni
Zgjidhje. Funksioni është përcaktuar në të gjithë vijën numerike përveç x= 0, d.m.th.
Prandaj, në pikën e thyerjes x= 0 kurba mund të ketë një asimptotë vertikale. Në të vërtetë, kufiri i funksionit kur x tenton në zero nga e majta është i barabartë me plus pafundësinë:


Prandaj, x= 0 – asimptotë vertikale e grafikut të këtij funksioni.
Grafiku i këtij funksioni nuk ka një asimptotë horizontale, pasi kufiri i funksionit kur x tenton në plus pafundësi është i barabartë me plus pafundësinë:
![]()
Le të zbulojmë praninë e një asimptote të zhdrejtë:

Ka kufij të fundëm k= 2 dhe b= 0. Drejt y = 2xështë asimptota e pjerrët dykahëshe e grafikut të këtij funksioni (figura brenda shembullit).
Shembulli 7. Gjeni asimptota të grafikut të një funksioni
Zgjidhje. Funksioni ka një pikë pushimi x= −1. Le të llogarisim kufijtë e njëanshëm dhe të përcaktojmë llojin e ndërprerjes:
konkluzioni: x= −1 është një pikë ndërprerjeje e llojit të dytë, pra vija e drejtë x= −1 është asimptota vertikale e grafikut të këtij funksioni.
Po kërkojmë asimptota të zhdrejta. Meqenëse ky funksion është fraksional-racional, kufijtë sipas dëshirës dhe sipas dëshirës përkojnë. Kështu, gjejmë koeficientët për zëvendësimin e vijës së drejtë - asimptotës së zhdrejtë në ekuacionin:


Duke zëvendësuar koeficientët e gjetur në ekuacionin e vijës së drejtë me koeficientin e pjerrësisë, marrim ekuacionin e asimptotës së zhdrejtë:
y = −3x + 5 .
Në figurë, grafiku i funksionit tregohet në ngjyrë burgundy, dhe asimptotat tregohen me ngjyrë të zezë.
Shembulli 8. Gjeni asimptota të grafikut të një funksioni
Zgjidhje. Meqenëse ky funksion është i vazhdueshëm, grafiku i tij nuk ka asimptota vertikale. Ne jemi duke kërkuar për asimptota të zhdrejtë:
 .
.
Kështu, grafiku i këtij funksioni ka një asimptotë y= 0 në dhe nuk ka asiptotë në .

Shembulli 9. Gjeni asimptota të grafikut të një funksioni
Zgjidhje. Së pari ne kërkojmë asimptota vertikale. Për ta bërë këtë, gjejmë domenin e përkufizimit të funksionit. Një funksion përcaktohet kur pabarazia dhe . Shenja e ndryshores x përputhet me shenjën. Prandaj, merrni parasysh pabarazinë ekuivalente. Nga kjo marrim domenin e përkufizimit të funksionit: ![]() . Një asimptotë vertikale mund të jetë vetëm në kufirin e fushës së përcaktimit të funksionit. Por x= 0 nuk mund të jetë një asimptotë vertikale, pasi funksioni është përcaktuar në x = 0
.
. Një asimptotë vertikale mund të jetë vetëm në kufirin e fushës së përcaktimit të funksionit. Por x= 0 nuk mund të jetë një asimptotë vertikale, pasi funksioni është përcaktuar në x = 0
.
Konsideroni kufirin e djathtë në (nuk ka kufi në të majtë):
![]() .
.
Pika x= 2 është një pikë ndërprerjeje e llojit të dytë, pra vija e drejtë x= 2 - asimptotë vertikale e grafikut të këtij funksioni.
Ne jemi duke kërkuar për asimptota të zhdrejtë:

Pra, y = x+ 1 - asimptotë e zhdrejtë e grafikut të këtij funksioni në . Ne jemi duke kërkuar për një asimptotë të zhdrejtë në:
Pra, y = −x − 1 - asimptotë e zhdrejtë në .

Shembulli 10. Gjeni asimptota të grafikut të një funksioni
Zgjidhje. Një funksion ka një fushë përkufizimi ![]() . Meqenëse asimptota vertikale e grafikut të këtij funksioni mund të jetë vetëm në kufirin e fushës së përkufizimit, ne gjejmë kufijtë e njëanshëm të funksionit në .
. Meqenëse asimptota vertikale e grafikut të këtij funksioni mund të jetë vetëm në kufirin e fushës së përkufizimit, ne gjejmë kufijtë e njëanshëm të funksionit në .
Asimptotat e grafikut të një funksioni
Fantazma e asimptotës ka bredhur rreth faqes për një kohë të gjatë për t'u materializuar më në fund në një artikull të veçantë dhe për të sjellë kënaqësi të veçantë për lexuesit në mëdyshje studimi i plotë i funksionit. Gjetja e asimptotave të grafikut është një nga pjesët e pakta të detyrës së specifikuar, e cila mbulohet në kursin e shkollës vetëm në mënyrë të përgjithshme, pasi ngjarjet rrotullohen rreth llogaritjes. kufijtë e funksionit, por gjithsesi i përkasin matematikës së lartë. Për vizitorët që kanë pak njohuri nga analiza matematikore, mendoj se sugjerimi është i qartë ;-) ...ndalo, ndalo, ku po shkon? Limitet- është e lehtë!
Shembuj asimptotash u ndeshën menjëherë në mësimin e parë rreth grafikët e funksioneve elementare, dhe tema tani po merr një shqyrtim të detajuar.
Pra, çfarë është një asimptotë?
Imagjinoni pikë e ndryshueshme, i cili “udhëton” përgjatë grafikut të funksionit. Asimptota është drejt, tek e cila mbyllet pafundësisht grafiku i një funksioni afrohet ndërsa pika e tij e ndryshueshme lëviz në pafundësi.
Shënim : Përkufizimi është kuptimplotë, nëse ju nevojitet formulimi në shënimin e llogaritjes, ju lutemi referojuni tekstit shkollor.
Në aeroplan, asimptotat klasifikohen sipas vendndodhjes së tyre natyrore:
1) Asimptota vertikale, të cilat jepen nga një ekuacion i formës , ku është "alfa". numër real. Një përfaqësues popullor përcakton vetë boshtin e ordinatave,
me një ndjenjë të lehtë nauzeje kujtojmë hiperbolën.
2) Asimptota të zhdrejta shkruar tradicionalisht ekuacioni i një vije të drejtë me një koeficient këndor. Ndonjëherë një rast i veçantë identifikohet si një grup i veçantë - asimptota horizontale. Për shembull, e njëjta hiperbolë me asimptotë.
Le të shkojmë shpejt, le ta godasim temën me një shpërthim të shkurtër të mitralozit:
Sa asimptota mund të ketë grafiku i një funksioni?
Jo një, një, dy, tre, ... ose pafundësisht shumë. Ne nuk do të shkojmë larg për shembuj, le të kujtojmë funksionet elementare. Një parabolë, një parabolë kubike dhe një valë sinusale nuk kanë fare asimptota. Grafiku i një funksioni logaritmik eksponencial ka një asimptotë të vetme. Arktangjentja dhe arkotangjentja kanë dy prej tyre, dhe tangjentja dhe kotangjentja kanë pafundësisht shumë. Nuk është e pazakontë që një grafik të ketë asimptota horizontale dhe vertikale. Hiperbola, do të të dua gjithmonë.
Çfarë do të thotë?
Asimptotat vertikale të grafikut të një funksioni
Zakonisht gjendet asimptota vertikale e grafikut në pikën e ndërprerjes së pafundme funksionet. Është e thjeshtë: nëse në një pikë funksioni pëson një ndërprerje të pafundme, atëherë vija e drejtë e specifikuar nga ekuacioni është asimptota vertikale e grafikut.
Shënim : Vini re se hyrja përdoret për t'iu referuar dy koncepteve krejtësisht të ndryshme. Nëse një pikë nënkuptohet ose një ekuacion i një linje varet nga konteksti.
Kështu, për të vërtetuar praninë e një asimptote vertikale në një pikë, mjafton të tregohet se të paktën një nga kufijtë e njëanshëm ![]() e pafundme. Më shpesh kjo është pika ku emëruesi i funksionit është zero. Në thelb, ne kemi gjetur tashmë asimptota vertikale në shembujt e fundit të mësimit mbi vazhdimësinë e një funksioni. Por në disa raste ekziston vetëm një kufi i njëanshëm, dhe nëse është i pafund, atëherë përsëri - dashuroni dhe favorizoni asimptotën vertikale. Ilustrimi më i thjeshtë: dhe boshti i ordinatave (shih. Grafikët dhe vetitë e funksioneve elementare).
e pafundme. Më shpesh kjo është pika ku emëruesi i funksionit është zero. Në thelb, ne kemi gjetur tashmë asimptota vertikale në shembujt e fundit të mësimit mbi vazhdimësinë e një funksioni. Por në disa raste ekziston vetëm një kufi i njëanshëm, dhe nëse është i pafund, atëherë përsëri - dashuroni dhe favorizoni asimptotën vertikale. Ilustrimi më i thjeshtë: dhe boshti i ordinatave (shih. Grafikët dhe vetitë e funksioneve elementare).
Nga sa më sipër, del edhe një fakt i dukshëm: nëse funksioni është aktiv i vazhdueshëm, atëherë nuk ka asimptota vertikale. Për disa arsye më erdhi në mendje një parabolë. Vërtet, ku mund të "ngjisni" një vijë të drejtë këtu? ...po... e kuptoj... Ndjekësit e xhaxha Frojdit u bënë histerikë =)
Deklarata e kundërt është përgjithësisht e rreme: për shembull, funksioni nuk përcaktohet në të gjithë vijën numerike, por është plotësisht i privuar nga asimptota.
Asimptotat e pjerrëta të grafikut të një funksioni
Asimptotat e zhdrejta (si rast i veçantë - horizontale) mund të nxirren nëse argumenti i funksionit priret në "plus infinity" ose në "minus infinity". Kjo është arsyeja pse grafiku i një funksioni nuk mund të ketë më shumë se dy asimptota të pjerrëta. Për shembull, grafiku i një funksioni eksponencial ka një asimptotë të vetme horizontale në , dhe grafiku i arktangjentes në ka dy asimptota të tilla, dhe në atë të ndryshme.
Kur grafiku në të dy vendet i afrohet një asimptote të vetme të zhdrejtë, atëherë "pafundësitë" zakonisht kombinohen nën një hyrje të vetme. Për shembull, ...e keni marrë me mend saktë: .
Rregulli i përgjithshëm i përgjithshëm:
Nëse janë dy përfundimtar limit ![]() , atëherë drejtëza është asimptota e zhdrejtë e grafikut të funksionit në . Nëse të paktën një nga kufijtë e listuar është i pafund, atëherë nuk ka asimptotë të zhdrejtë.
, atëherë drejtëza është asimptota e zhdrejtë e grafikut të funksionit në . Nëse të paktën një nga kufijtë e listuar është i pafund, atëherë nuk ka asimptotë të zhdrejtë.
Shënim : formulat mbeten të vlefshme nëse "x" tenton vetëm në "plus pafundësi" ose vetëm në "minus pafundësi".
Le të tregojmë se parabola nuk ka asimptota të zhdrejta: ![]()
Kufiri është i pafund, që do të thotë se nuk ka asimptotë të zhdrejtë. Vini re se në gjetjen e kufirit ![]() nevoja është zhdukur pasi përgjigja tashmë është marrë.
nevoja është zhdukur pasi përgjigja tashmë është marrë.
Shënim
: Nëse keni (ose do të keni) vështirësi për të kuptuar shenjat plus-minus, minus-plus, ju lutemi shikoni ndihmën në fillim të mësimit
mbi funksionet infiniteminale, ku ju thashë se si t'i interpretoni saktë këto shenja.
Natyrisht, për çdo kuadratik, funksioni kub, një polinom i shkallës 4 dhe më të lartë gjithashtu nuk ka asimptota të zhdrejtë.
Tani le të sigurohemi që grafiku gjithashtu të mos ketë një asimptotë të zhdrejtë. Për të zbuluar pasigurinë ne përdorim Rregulli i L'Hopital:
, e cila ishte ajo që duhej të kontrollohej.
Megjithatë, kur funksioni rritet pafundësisht, nuk ka asnjë vijë të drejtë të cilës do t'i afrohej grafiku i tij pafundësisht afër.
Le të kalojmë në pjesën praktike të mësimit:
Si të gjejmë asimptotat e grafikut të një funksioni?
Pikërisht kështu është formuluar detyrë tipike, dhe përfshin gjetjen e TË GJITHA asimptotave të grafikut (vertikale, e pjerrët/horizontale). Edhe pse, për të qenë më të saktë në shtrimin e pyetjes, po flasim për kërkime për praninë e asimptotave (në fund të fundit, mund të mos ketë fare). Le të fillojmë me diçka të thjeshtë:
Shembulli 1
Gjeni asimptota të grafikut të një funksioni
ZgjidhjeËshtë e përshtatshme për ta ndarë atë në dy pika:
1) Fillimisht kontrollojmë nëse ka asimptota vertikale. Emëruesi shkon në zero në , dhe është menjëherë e qartë se në këtë pikë funksioni vuan hendek i pafund, dhe drejtëza e dhënë nga ekuacioni është asimptota vertikale e grafikut të funksionit. Por, para se të nxirret një përfundim i tillë, është e nevojshme të gjesh kufij të njëanshëm: 
Ju kujtoj teknikën e llogaritjes në të cilën u fokusova në mënyrë të ngjashme në artikull Vazhdimësia e funksionit. Pikat e pushimit. Në shprehjen nën shenjën e kufirit zëvendësojmë . Nuk ka asgjë interesante në numërues:
.
Por në emërues rezulton numër negativ pafundësisht i vogël:
, përcakton fatin e kufirit.
Kufiri i majtë është i pafund dhe, në parim, tashmë është e mundur të merret një vendim për praninë e një asimptote vertikale. Por kufijtë e njëanshëm nevojiten jo vetëm për këtë - ato NDIHMËNË TË KUPTOHEN SI gjeni grafikun e funksionit dhe ndërtoni atë SAKTE. Prandaj, duhet të llogarisim edhe kufirin e dorës së djathtë: 
konkluzioni: kufijtë e njëanshëm janë të pafund, që do të thotë se drejtëza është asimptota vertikale e grafikut të funksionit në .
Kufiri i parë të fundme, që do të thotë se është e nevojshme të "vazhdoni bisedën" dhe të gjeni kufirin e dytë:
Kufiri i dytë gjithashtu të fundme.
Pra, asimptota jonë është:
konkluzioni: drejtëza e dhënë nga ekuacioni është asimptota horizontale e grafikut të funksionit në .
Për të gjetur asimptotën horizontale
ju mund të përdorni një formulë të thjeshtuar:
Nëse ekziston të fundme kufi, atëherë drejtëza është asimptota horizontale e grafikut të funksionit në .
Është e lehtë të shihet se numëruesi dhe emëruesi i funksionit rend i njëjtë i rritjes, që do të thotë se kufiri i kërkuar do të jetë i kufizuar: 
Përgjigju:
Sipas kushtit, nuk keni nevojë të përfundoni vizatimin, por nëse është në lëvizje të plotë studimi i funksionit, pastaj në draft bëjmë menjëherë një skicë: 
Bazuar në tre kufijtë e gjetur, përpiquni të kuptoni vetë se si mund të vendoset grafiku i funksionit. A është fare e vështirë? Gjeni 5-6-7-8 pikë dhe shënojini ato në vizatim. Megjithatë, grafiku i këtij funksioni është ndërtuar duke përdorur shndërrimet e grafikut të një funksioni elementar, dhe lexuesit që shqyrtuan me kujdes Shembullin 21 të artikullit të mësipërm mund të marrin me mend lehtësisht se çfarë lloj lakore është kjo.
Shembulli 2
Gjeni asimptota të grafikut të një funksioni
Ky është një shembull që ju duhet ta zgjidhni vetë. Më lejoni t'ju kujtoj se procesi ndahet lehtësisht në dy pika - asimptota vertikale dhe asimptota të zhdrejtë. Në zgjidhjen e mostrës, asimptota horizontale gjendet duke përdorur një skemë të thjeshtuar.
Në praktikë, funksionet fraksionale-racionale hasen më shpesh, dhe pas trajnimit mbi hiperbolat, ne do ta komplikojmë detyrën:
Shembulli 3
Gjeni asimptota të grafikut të një funksioni ![]()
Zgjidhje: Një, dy dhe e mbaruar:
1) Gjenden asimptota vertikale në pikat e ndërprerjes së pafundme, kështu që ju duhet të kontrolloni nëse emëruesi shkon në zero. Le të vendosim ekuacioni kuadratik:![]()
Diskriminuesi është pozitiv, kështu që ekuacioni ka dy rrënjë reale dhe puna është rritur ndjeshëm =) 
Për të gjetur më tej kufijtë e njëanshëm, është e përshtatshme të faktorizohet trinomi katror:
(për shënimin kompakt, "minus" u përfshi në kllapin e parë). Për të qenë në anën e sigurt, le ta kontrollojmë duke hapur kllapat mendërisht ose në një draft.
Le ta rishkruajmë funksionin në formë ![]()
Le të gjejmë kufijtë e njëanshëm në pikën: 
Dhe në pikën: 
Pra, drejtëzat janë asimptota vertikale të grafikut të funksionit në fjalë.
2) Nëse shikoni funksionin ![]() , atëherë është mjaft e qartë se kufiri do të jetë i fundëm dhe kemi një asimptotë horizontale. Le të tregojmë prezencën e tij në një mënyrë të shkurtër:
, atëherë është mjaft e qartë se kufiri do të jetë i fundëm dhe kemi një asimptotë horizontale. Le të tregojmë prezencën e tij në një mënyrë të shkurtër: ![]()
Pra, drejtëza (boshti i abshisës) është asimptota horizontale e grafikut të këtij funksioni.
Përgjigju:
Kufijtë dhe asimptotat e gjetura japin shumë informacion rreth grafikut të funksionit. Mundohuni të imagjinoni mendërisht vizatimin duke marrë parasysh faktet e mëposhtme: 
Skico versionin tuaj të grafikut në draftin tuaj.
Natyrisht, kufijtë e gjetur nuk përcaktojnë qartë pamjen e grafikut dhe mund të bëni një gabim, por vetë ushtrimi do të japë ndihmë të paçmuar gjatë studim i plotë i funksionit. Fotografia e saktë është në fund të mësimit.
Shembulli 4
Gjeni asimptota të grafikut të një funksioni
Shembulli 5
Gjeni asimptota të grafikut të një funksioni ![]()
Këto janë detyra për zgjidhje të pavarur. Të dy grafikët kanë përsëri asimptota horizontale, të cilat zbulohen menjëherë nga karakteristikat e mëposhtme: në shembullin 4 rendi i rritjes emërues më shumë, se rendi i rritjes së numëruesit, dhe në shembullin 5 numëruesi dhe emëruesi rend i njëjtë i rritjes. Në zgjidhjen e mostrës, funksioni i parë ekzaminohet për praninë e asimptotave të zhdrejtë plotësisht, dhe i dyti - përmes kufirit.
Asimptotat horizontale, sipas përshtypjes sime subjektive, janë dukshëm më të zakonshme se ato që janë "me të vërtetë të anuara". Rasti i përgjithshëm i shumëpritur:
Shembulli 6
Gjeni asimptota të grafikut të një funksioni ![]()
Zgjidhje: klasik i zhanrit:
1) Meqenëse emëruesi është pozitiv, atëherë funksioni të vazhdueshme përgjatë gjithë vijës numerike dhe nuk ka asimptota vertikale. ...A është mirë kjo? Nuk është fjala e duhur - e shkëlqyer! Pika nr.1 është e mbyllur.
2) Le të kontrollojmë praninë e asimptotave të zhdrejtë:
Kufiri i parë të fundme, kështu që le të vazhdojmë. Gjatë llogaritjes së kufirit të dytë për të eliminuar pasiguri "pafundësi minus pafundësi" Ne e sjellim shprehjen në një emërues të përbashkët: 
Kufiri i dytë gjithashtu të fundme Prandaj, grafiku i funksionit në fjalë ka një asimptotë të zhdrejtë:
konkluzioni:
Kështu, kur grafiku i funksionit ![]() pafundësisht afër afrohet në një vijë të drejtë:
pafundësisht afër afrohet në një vijë të drejtë: 
Vini re se ajo kryqëzon asimptotën e saj të zhdrejtë në origjinë, dhe pika të tilla kryqëzimi janë mjaft të pranueshme - është e rëndësishme që "gjithçka të jetë normale" në pafundësi (në fakt, këtu po flasim për asimptota).
Shembulli 7
Gjeni asimptota të grafikut të një funksioni
Zgjidhje: Nuk ka asgjë të veçantë për të komentuar, kështu që unë do të hartoj një shembull të përafërt të një zgjidhjeje të pastër:
1) Asimptota vertikale. Le të shqyrtojmë pikën. 
Vija e drejtë është asimptota vertikale për grafikun në .
2) Asimptota të zhdrejtë: 
Vija e drejtë është asimptota e pjerrët për grafikun në .
Përgjigju: ![]()
Kufijtë dhe asimptotat e gjetura të njëanshme na lejojnë të parashikojmë me siguri të lartë se si duket grafiku i këtij funksioni. Vizatimi i saktë në fund të mësimit.
Shembulli 8
Gjeni asimptota të grafikut të një funksioni
Ky është një shembull për zgjidhje të pavarur, për lehtësinë e llogaritjes së disa kufijve, mund ta ndani numëruesin me emëruesin sipas termit. Përsëri, kur analizoni rezultatet tuaja, përpiquni të vizatoni një grafik të këtij funksioni.
Natyrisht, pronarët e asimptotave të zhdrejta "të vërteta" janë grafikët e atyre funksionet racionale thyesore, të cilat kanë një shkallë më të lartë të numëruesit një më shumë shkalla më e lartë e emëruesit. Nëse është më shumë, nuk do të ketë asimptotë të zhdrejtë (për shembull, ).
Por në jetë ndodhin mrekulli të tjera:
Shembulli 9
![]()
Shembulli 11
Shqyrtoni grafikun e një funksioni për praninë e asimptotave
Zgjidhje: është e qartë se ![]() , prandaj konsiderojmë vetëm gjysmërrafshin e djathtë, ku ka një grafik të funksionit.
, prandaj konsiderojmë vetëm gjysmërrafshin e djathtë, ku ka një grafik të funksionit.
Kështu, drejtëza (boshti i ordinatave) është asimptota vertikale për grafikun e funksionit në .
2) Studimi mbi asimptotën e zhdrejtë mund të kryhet sipas skemës së plotë, por në artikull Rregullat e L'Hopital ne zbuluam se funksion linear rend më i lartë i rritjes se logaritmik, prandaj: ![]() (Shih Shembullin 1 të të njëjtit mësim).
(Shih Shembullin 1 të të njëjtit mësim).
Përfundim: boshti x është asimptota horizontale e grafikut të funksionit në .
Përgjigju:
, Nëse ;
, Nëse .
Vizatim për qartësi: 
Është interesante që një funksion në dukje i ngjashëm nuk ka fare asimptota (ata që dëshirojnë mund ta kontrollojnë këtë).
Dy shembuj të fundit për vetë-studim:
Shembulli 12
Shqyrtoni grafikun e një funksioni për praninë e asimptotave ![]()
Zgjidhja mund të ndahet lehtësisht në dy pika:
1) Fillimisht kontrollojmë nëse ka asimptota vertikale. Emëruesi shkon në zero në, dhe është menjëherë e qartë se në këtë pikë funksioni pëson një ndërprerje të pafundme, dhe vija e drejtë e specifikuar nga ekuacioni është asimptota vertikale e grafikut të funksionit. Por, para se të nxirret një përfundim i tillë, është e nevojshme të gjesh kufij të njëanshëm:

Ju kujtoj teknikën e llogaritjes që në mënyrë të ngjashme u fokusova në artikullin Vazhdimësia e një funksioni. Pikat e thyerjes. Ne zëvendësojmë "X" në shprehjen nën shenjën e kufirit. Nuk ka asgjë interesante në numërues:
Por emëruesi rezulton në një numër negativ pafundësisht të vogël:
Ai përcakton fatin e kufirit.
Kufiri i majtë është i pafund dhe, në parim, tashmë është e mundur të merret një vendim për praninë e një asimptote vertikale. Por kufijtë e njëanshëm nevojiten jo vetëm për këtë - ato NDIHMOJNË PËR TË KUPTUAR SI gjendet grafiku i një funksioni dhe për ta ndërtuar atë SAKT. Prandaj, duhet të llogarisim edhe kufirin e dorës së djathtë:

Përfundim: kufijtë e njëanshëm janë të pafund, që do të thotë se drejtëza është asimptota vertikale e grafikut të funksionit në.
Kufiri i parë është i kufizuar, që do të thotë se ne duhet të "vazhdojmë bisedën" dhe të gjejmë kufirin e dytë:
Kufiri i dytë është gjithashtu i kufizuar.
Pra, asimptota jonë është:
Përfundim: drejtëza e përcaktuar nga ekuacioni është asimptota horizontale e grafikut të funksionit në.
Për të gjetur asimptotën horizontale, mund të përdorni një formulë të thjeshtuar:
Nëse ka një kufi të fundëm, atëherë vija e drejtë është asimptota horizontale e grafikut të funksionit në.
Është e lehtë të vërehet se numëruesi dhe emëruesi i funksionit janë të rendit të njëjtë të rritjes, që do të thotë se kufiri i kërkuar do të jetë i fundëm:

Sipas kushtit, nuk ka nevojë të bëjmë një vizatim, por nëse jemi në mes të kërkimit të një funksioni, atëherë menjëherë bëjmë një skicë në draft:

Bazuar në tre kufijtë e gjetur, përpiquni të kuptoni vetë se si mund të vendoset grafiku i funksionit. A është fare e vështirë? Gjeni 5-6-7-8 pikë dhe shënojini ato në vizatim. Megjithatë, grafiku i këtij funksioni është ndërtuar duke përdorur transformimet e grafikut funksioni elementar, dhe lexuesit që shqyrtuan me kujdes Shembullin 21 të artikullit të mësipërm mund të marrin me mend lehtësisht se çfarë lloj lakore është kjo.
Ky është një shembull që ju duhet ta zgjidhni vetë. Më lejoni t'ju kujtoj se procesi ndahet lehtësisht në dy pika - asimptota vertikale dhe asimptota të zhdrejtë. Në zgjidhjen e mostrës, asimptota horizontale gjendet duke përdorur një skemë të thjeshtuar.
Në praktikë, funksionet fraksionale-racionale hasen më shpesh, dhe pas trajnimit mbi hiperbolat, ne do ta komplikojmë detyrën:
Gjeni asimptota të grafikut të një funksioni
Zgjidhja: Një, dy dhe e përfunduar:
1) Asimptotat vertikale janë në pika të ndërprerjes së pafundme, kështu që ju duhet të kontrolloni nëse emëruesi shkon në zero. Le të vendosim ekuacioni kuadratik:
Diskriminuesi është pozitiv, kështu që ekuacioni ka dy rrënjë reale dhe puna shtohet ndjeshëm

Për të gjetur më tej kufijtë e njëanshëm, është e përshtatshme të faktorizohet trinomi katror:
(për shënimin kompakt, "minus" u përfshi në kllapin e parë). Për të qenë në anën e sigurt, le ta kontrollojmë duke hapur kllapat mendërisht ose në një draft.
Le ta rishkruajmë funksionin në formë
Le të gjejmë kufijtë e njëanshëm në pikën:

kufiri i funksionit të grafikut asimptotë
Dhe në pikën:

Pra, drejtëzat janë asimptota vertikale të grafikut të funksionit në fjalë.
2) Nëse shikoni funksionin, është mjaft e qartë se kufiri do të jetë i fundëm dhe kemi një asimptotë horizontale. Le të tregojmë prezencën e tij në një mënyrë të shkurtër:
Pra, drejtëza (boshti i abshisës) është asimptota horizontale e grafikut të këtij funksioni.
Kufijtë dhe asimptotat e gjetura japin shumë informacion rreth grafikut të funksionit. Mundohuni të imagjinoni mendërisht vizatimin duke marrë parasysh faktet e mëposhtme:

Skico versionin tuaj të grafikut në draftin tuaj.
Sigurisht, kufijtë e gjetur nuk përcaktojnë qartë pamjen e grafikut dhe mund të bëni një gabim, por vetë ushtrimi do të ofrojë ndihmë të paçmuar gjatë një studimi të plotë të funksionit. Fotografia e saktë është në fund të mësimit.
Gjeni asimptota të grafikut të një funksioni
Gjeni asimptota të grafikut të një funksioni
Këto janë detyra për zgjidhje të pavarur. Të dy grafikët kanë përsëri asimptota horizontale, të cilat zbulohen menjëherë nga karakteristikat e mëposhtme: në shembullin 4, rendi i rritjes së emëruesit është më i madh se rendi i rritjes së numëruesit, dhe në shembullin 5, numëruesi dhe emëruesi janë të rend i njëjtë i rritjes. Në zgjidhjen e mostrës, funksioni i parë ekzaminohet për praninë e asimptotave të zhdrejtë plotësisht, dhe i dyti - përmes kufirit.
Asimptotat horizontale, sipas përshtypjes sime subjektive, janë dukshëm më të zakonshme se ato që janë "me të vërtetë të anuara". Rasti i përgjithshëm i shumëpritur:
Gjeni asimptota të grafikut të një funksioni
Zgjidhja: klasike e zhanrit:
- 1) Meqenëse emëruesi është pozitiv, funksioni është i vazhdueshëm përgjatë gjithë vijës numerike dhe nuk ka asimptota vertikale. ...A është mirë kjo? Nuk është fjala e duhur - e shkëlqyer! Pika nr.1 është e mbyllur.
- 2) Le të kontrollojmë praninë e asimptotave të zhdrejtë:

Kufiri i dytë është gjithashtu i fundëm, prandaj, grafiku i funksionit në fjalë ka një asimptotë të zhdrejtë:
Kështu, kur grafiku i funksionit i afrohet një drejtëze pafundësisht afër.
Vini re se ajo kryqëzon asimptotën e saj të zhdrejtë në origjinë, dhe pika të tilla kryqëzimi janë mjaft të pranueshme - është e rëndësishme që "gjithçka të jetë normale" në pafundësi (në fakt, këtu po flasim për asimptota).

Gjeni asimptota të grafikut të një funksioni
Zgjidhja: nuk ka asgjë të veçantë për të komentuar, kështu që unë do të hartoj një shembull të përafërt të një zgjidhjeje përfundimtare:
1) Asimptota vertikale. Le të shqyrtojmë pikën.

Vija e drejtë është asimptota vertikale për grafikun në.
2) Asimptota të zhdrejtë:

Vija e drejtë është asimptota e pjerrët për grafikun në.
Kufijtë dhe asimptotat e gjetura të njëanshme na lejojnë të parashikojmë me siguri të lartë se si duket grafiku i këtij funksioni.
Gjeni asimptota të grafikut të një funksioni
Ky është një shembull për zgjidhje të pavarur, për lehtësinë e llogaritjes së disa kufijve, mund ta ndani numëruesin me emëruesin sipas termit. Përsëri, kur analizoni rezultatet tuaja, përpiquni të vizatoni një grafik të këtij funksioni.
Natyrisht, pronarët e asimptotave të zhdrejta "reale" janë grafikët e atyre funksioneve racionale thyesore në të cilat shkalla më e lartë e numëruesit është një më e madhe se shkalla më e lartë e emëruesit. Nëse është më shumë, nuk do të ketë më asimptotë të zhdrejtë (për shembull).
Por në jetë ndodhin mrekulli të tjera.
 Kronologjia gjeologjike Metoda paleontologjike bazohet në studimin e organizmave fosile dhe bimëve të varrosura në shtresa shkëmbore
Kronologjia gjeologjike Metoda paleontologjike bazohet në studimin e organizmave fosile dhe bimëve të varrosura në shtresa shkëmbore Mitet për krijimtarinë që rezultuan të pavërteta, por gjithsesi na helmojnë jetën
Mitet për krijimtarinë që rezultuan të pavërteta, por gjithsesi na helmojnë jetën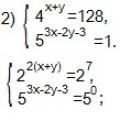 Zgjidhja e ekuacioneve dhe pabarazive eksponenciale
Zgjidhja e ekuacioneve dhe pabarazive eksponenciale