Konstruiranje tangente na tangentne krožnice. Relativni položaj dveh krogov
Običajno vam je pri takšni nalogi dana krog in točka. Konstruirati je treba tangento na krožnico, tangenta pa mora potekati skozi dano točko.
Če lokacija točke ni navedena, je treba posebej določiti tri možne primere lokacije točke.
- Če točka leži znotraj kroga, ki ga omejuje dani krog, potem skozi to ni mogoče konstruirati tangente.
- Če točka leži na krožnici, se tangenta konstruira tako, da sestavi premica, pravokotna na polmer, narisan na dano točko.
- Če točka leži zunaj kroga, ki ga omejuje krog, se pred konstruiranjem tangente išče točka na krogu, skozi katero mora potekati.
Za rešitev drugega primera se na premici, na kateri leži polmer, konstruira odsek, ki je enak polmeru in leži na drugi strani točke na krogu. Tako se točka na krogu izkaže za sredino segmenta, ki je enak dvakratnemu polmeru. Nato sta sestavljena dva kroga, katerih polmera sta enaka dvakratnemu polmeru prvotnega kroga, s središči na koncih segmenta, ki sta enaka dvakratnemu polmeru. Skozi katero koli točko presečišča teh krogov in točko, določeno s pogoji problema, je narisana ravna črta. To bo mediana, pravokotna na polmer prvotnega kroga, to je pravokotna nanj in torej tangentna na krog.
Tretji primer, ko točka leži zunaj kroga, ki ga omejuje krog, lahko rešite takole. Treba je zgraditi segment, ki povezuje središče danega kroga in dano točko. Nato poiščite njegovo sredino tako, da sestavite sredinsko pravokotno (opisano v prejšnjem odstavku). Po tem narišite krog (ali njegov del). Točka presečišča konstruirane krožnice in tiste, ki jo določajo problemski pogoji, je točka, skozi katero poteka tangenta, ki prav tako poteka skozi točko, določeno s problemskimi pogoji. Skozi dve znani točki je narisana tangenta.
Da bi dokazali, da je konstruirana ravna črta tangenta, je treba upoštevati kot, ki ga tvorita polmer kroga, ki ga določajo pogoji problema, in odsek, ki povezuje presečišče krogov s točko, ki ga določajo pogoji problem. Ta kot se opira na polkrog (premer sestavljenega kroga), kar pomeni, da je raven. To pomeni, da je polmer pravokoten na konstruirano črto. Zato je zgrajena premica tangentna.
Cilji lekcije
- Izobraževalno – ponavljanje, posploševanje in preverjanje znanja na temo: »Tangenta na krožnico«; razvoj osnovnih veščin.
- Razvojni - razviti pozornost učencev, vztrajnost, vztrajnost, logično razmišljanje, matematični govor.
- Izobraževalni - skozi lekcijo gojite pozoren odnos drug do drugega, vcepljajte sposobnost poslušanja tovarišev, medsebojne pomoči in neodvisnosti.
- Predstavite pojem tangenta, stična točka.
- Upoštevajte lastnost tangente in njenega predznaka ter pokažite njuno uporabo pri reševanju problemov v naravi in tehniki.
Cilji lekcije
- Razviti veščine konstruiranja tangent z uporabo ravnila, kotomerja in risalnega trikotnika.
- Preizkusite sposobnosti študentov za reševanje problemov.
- Zagotoviti obvladovanje osnovnih algoritemskih tehnik za konstruiranje tangente na krožnico.
- Razviti sposobnost uporabe teoretičnega znanja pri reševanju problemov.
- Razvijati mišljenje in govor učencev.
- Delajte na razvijanju veščin opazovanja, opazovanja vzorcev, posploševanja in sklepanja po analogiji.
- Vzbujanje zanimanja za matematiko.
Načrt lekcije
- Nastanek koncepta tangente.
- Zgodovina pojava tangente.
- Geometrijske definicije.
- Osnovni izreki.
- Konstruiranje tangente na krožnico.
- Utrjevanje.
Nastanek koncepta tangente
Koncept tangente je eden najstarejših v matematiki. V geometriji je tangenta na krog definirana kot črta, ki ima natanko eno presečišče s tem krogom. Starodavni so s pomočjo šestila in ravnila znali risati tangente na krožnico, pozneje pa na stožčaste preseke: elipse, hiperbole in parabole.
Zgodovina tangente
Zanimanje za tangente je oživelo v sodobnem času. Nato so odkrili krivulje, ki jih stari znanstveniki niso poznali. Galileo je na primer uvedel cikloido, Descartes in Fermat pa sta zgradila tangento nanjo. V prvi tretjini 17. stol. Začeli smo razumeti, da je tangenta ravna črta, ki »najbližje meji« na krivuljo v majhni okolici dane točke. Zlahka si je predstavljati situacijo, ko je nemogoče zgraditi tangento na krivuljo v dani točki (slika). 
Geometrijske definicije
krog- geometrijsko mesto točk na ravnini, enako oddaljenih od dane točke, ki se imenuje njeno središče.
 krog.
krog.
Sorodne definicije
- Imenuje se segment, ki povezuje središče kroga s katero koli točko na njem (kot tudi dolžino tega segmenta). polmer krogih.
- Del ravnine, ki ga omejuje krog, imenujemo vse naokoli.
- Odsek, ki povezuje dve točki na krogu, se imenuje njegov akord. Imenuje se tetiva, ki poteka skozi središče kroga premer.
- Vsaki dve različni točki na krogu ga razdelita na dva dela. Vsak od teh delov se imenuje lok krogih. Mera loka je lahko mera njegovega ustreznega središčnega kota. Lok se imenuje polkrog, če je segment, ki povezuje njegove konce, premer.
- Premica, ki ima s krožnico točno eno skupno točko, se imenuje tangenta na krožnico, njuno skupno točko pa imenujemo stičišče premice in krožnice.
- Imenuje se premica, ki poteka skozi dve točki na krožnici sekant.
- Osrednji kot v krogu je ravninski kot z ogliščem v središču.
- Kot, katerega vrh leži na krogu in katerega stranice sekajo ta krog, se imenuje vpisan kot.
- Dva kroga s skupnim središčem se imenujeta koncentrično.
Tangentna črta- ravna črta, ki poteka skozi točko na krivulji in sovpada z njo na tej točki do prvega reda.

Tangenta na krožnico je premica, ki ima s krožnico eno skupno točko.

Ravna črta, ki poteka skozi točko na krogu v isti ravnini, pravokotni na polmer, narisan na to točko imenovano tangenta. V tem primeru se ta točka na krogu imenuje tangentna točka.
Če je v naših primerih "a" ravna črta, ki se dotika danega kroga, je točka "A" točka dotika. V tem primeru je a⊥OA (premica a je pravokotna na polmer OA).
To pravijo dva kroga se dotikata, če imata eno skupno točko. Ta točka se imenuje stična točka krogov. Skozi stičišče lahko potegnemo tangento na eno od krožnic, ki je tudi tangenta na drugo krožnico. Dotikajoči se krogi so lahko notranji ali zunanji.
Tangenta se imenuje notranja, če središča krogov ležijo na isti strani tangente.
Tangenta se imenuje zunanja, če središča krogov ležijo na nasprotnih straneh tangente




a je skupna tangenta obeh krožnic, K je dotična točka.
Osnovni izreki
Izrek o tangenti in sekanti
Če iz točke, ki leži zunaj kroga, potegnemo tangento in sekanto, je kvadrat dolžine tangente enak zmnožku sekante in njenega zunanjega dela: MC 2 = MA MB.
Izrek. Polmer, narisan na tangentno točko kroga, je pravokoten na tangento.
Izrek.Če je polmer pravokoten na premico v točki, kjer seka krog, potem se ta premica dotika tega kroga.
Dokaz.
Da bi dokazali te izreke, se moramo spomniti, kaj je navpičnica iz točke na premico. To je najkrajša razdalja od te točke do te črte. Predpostavimo, da OA ni pravokotna na tangento, ampak obstaja premica OS, pravokotna na tangento. Dolžina OS vključuje dolžino polmera in določeno odsek BC, ki je zagotovo večji od polmera. Tako lahko to dokažemo za katero koli črto. Sklepamo, da je radij, polmer, narisan do stične točke, najkrajša razdalja do tangente iz točke O, tj. OS je pravokotna na tangento. Pri dokazu obratnega izreka bomo izhajali iz dejstva, da ima tangenta s krožnico samo eno skupno točko. Naj ima ta premica s krožnico še eno skupno točko B. Trikotnik AOB je pravokoten in njegovi strani sta enaki kot polmera, kar pa ne more biti tako. Tako ugotovimo, da ta premica nima več skupnih točk s krožnico razen točke A, tj. je tangenta.
Izrek. Odseki tangente, narisani iz ene točke na krog, so enaki, premica, ki to točko povezuje s središčem kroga, pa deli kot med tangentama.
Dokaz.
Dokaz je zelo preprost. Z uporabo prejšnjega izreka trdimo, da je OB pravokotna na AB, OS pa pravokotna na AC. Pravokotna trikotnika ABO in ACO sta enaka po kraku in hipotenuzi (OB=OS - polmeri, AO - skupaj). Zato sta njuni stranici AB=AC in kota OAC in OAB enaki.
Izrek. Velikost kota, ki ga tvorita tangenta in tetiva s skupno točko na krožnici, je enaka polovici kotne velikosti loka, ki je sklenjen med njunima stranicama.
Dokaz.
Razmislite o kotu NAB, ki ga tvorita tangenta in tetiva. Narišimo premer AC. Tangenta je pravokotna na premer, narisan na točko stika, zato je ∠CAN=90 o. Ob poznavanju izreka vidimo, da je kot alfa (a) enak polovici kotne vrednosti loka BC oziroma polovici kota BOS. ∠NAB=90 o -a, od tu dobimo ∠NAB=1/2(180 o -∠BOC)=1/2∠AOB ali = polovica kotne vrednosti loka BA. itd.
Izrek.Če tangento in sekanto narišemo iz točke na krožnico, potem je kvadrat tangente od dane točke do tangentne točke enak zmnožku dolžin sekante od dane točke do točk kroga. njegovo presečišče s krožnico.
Dokaz.
Na sliki je ta izrek videti takole: MA 2 = MV * MC. Dokažimo. Po prejšnjem izreku je kot MAC enak polovici kotne vrednosti loka AC, prav tako pa je kot ABC enak polovici kotne vrednosti loka AC po izreku, torej sta ta kota enaka vsakemu drugo. Upoštevajoč dejstvo, da imata trikotnika AMC in BMA skupni kot pri oglišču M, ugotavljamo podobnost teh trikotnikov v dveh kotih (drugi znak). Iz podobnosti imamo: MA/MB=MC/MA, iz česar dobimo MA 2 =MB*MC
Konstruiranje tangent na krožnico
Zdaj pa poskusimo ugotoviti in ugotoviti, kaj je treba storiti, da sestavimo tangento na krog.
V tem primeru praviloma problem poda krog in točko. In ti in jaz morava konstruirati tangento na krožnico, tako da ta tangenta poteka skozi dano točko.
V primeru, da lokacije točke ne poznamo, potem razmislimo o primerih možnih lokacij točk.
Prvič, točka je lahko znotraj kroga, ki je omejen z danim krogom. V tem primeru ni mogoče zgraditi tangente skozi ta krog.
V drugem primeru se točka nahaja na krožnici in lahko sestavimo tangento tako, da na polmer narišemo pravokotno črto, ki je narisana na nam znano točko.
Tretjič, predpostavimo, da se točka nahaja zunaj kroga, ki je omejen s krogom. V tem primeru je treba pred konstruiranjem tangente najti točko na krogu, skozi katero mora potekati tangenta.
Upam, da vam je v prvem primeru vse jasno, toda za rešitev druge možnosti moramo zgraditi segment na ravni črti, na kateri leži polmer. Ta segment mora biti enak polmeru in segmentu, ki leži na krogu na nasprotni strani.

Tukaj vidimo, da je točka na krogu sredina segmenta, ki je enak dvakratnemu polmeru. Naslednji korak bo izdelava dveh krogov. Polmeri teh krogov bodo enaki dvakratnemu polmeru prvotnega kroga s središči na koncih segmenta, ki je enak dvakratnemu polmeru. Zdaj lahko narišemo premico skozi poljubno presečišče teh krogov in dane točke. Takšna ravna črta je mediana, pravokotna na polmer kroga, ki je bil prvotno narisan. Tako vidimo, da je ta premica pravokotna na krog in iz tega sledi, da se dotika kroga.
Pri tretji možnosti imamo točko, ki leži izven krožnice, ki je omejena s krožnico. V tem primeru najprej sestavimo odsek, ki bo povezoval središče navedenega kroga in dano točko. In potem najdemo njegovo sredino. Toda za to je potrebno zgraditi pravokotno simetralo. In že veste, kako ga zgraditi. Nato moramo narisati krog ali vsaj njegov del. Sedaj vidimo, da je presečišče danega kroga in novokonstruiranega kroga točka, skozi katero poteka tangenta. Prav tako poteka skozi točko, ki je bila določena glede na pogoje problema. In končno, skozi dve točki, ki ju poznaš, lahko narišeš tangento.
In končno, da bi dokazali, da je ravna črta, ki smo jo zgradili, tangenta, moramo biti pozorni na kot, ki ga tvorita polmer kroga in segment, znan po pogoju in povezuje presečišče krogov s točko, ki jo določa pogoj problema. Zdaj vidimo, da nastali kot leži na polkrogu. In iz tega sledi, da je ta kot pravi. Posledično bo polmer pravokoten na novo zgrajeno premico in ta premica je tangenta.
Konstrukcija tangente.
Konstrukcija tangentnih črt je eden tistih problemov, ki so pripeljali do rojstva diferencialnega računa. Prvo objavljeno delo v zvezi z diferencialnim računom, ki ga je napisal Leibniz, je bilo naslovljeno »Nova metoda maksimumov in minimumov ter tangent, za katere niso ovira niti frakcijske niti iracionalne količine niti posebna vrsta računa«.
Geometrijsko znanje starih Egipčanov.
Če ne upoštevamo zelo skromnega prispevka starih prebivalcev doline med Tigrisom in Evfratom ter Male Azije, potem je geometrija nastala v starem Egiptu pred letom 1700 pr. Med tropskim deževnim obdobjem je Nil obnovil zaloge vode in se razlil. Voda je prekrila obdelovalne površine, za davčne namene pa je bilo treba ugotoviti, koliko zemlje je bilo izgubljeno. Geodeti so kot merilno orodje uporabljali tesno napeto vrv. Druga spodbuda za kopičenje geometrijskega znanja pri Egipčanih so bile njihove dejavnosti, kot sta gradnja piramid in likovna umetnost.
O stopnji geometrijskega znanja je mogoče soditi po starodavnih rokopisih, ki so posebej posvečeni matematiki in so nekaj podobnega učbenikom ali bolje rečeno knjigam problemov, kjer so podane rešitve različnih praktičnih problemov.
Najstarejši matematični rokopis Egipčanov je med letoma 1800 in 1600 prepisal neki študent. pr. n. št iz starejšega besedila. Papirus je našel ruski egiptolog Vladimir Semenovič Goleniščev. Hrani se v Moskvi - v Muzeju lepih umetnosti po imenu A.S. Puškina in se imenuje moskovski papirus.
Še en matematični papirus, napisan dvesto do tristo let pozneje od moskovskega, hranijo v Londonu. Imenuje se: “Navodilo, kako doseči spoznanje o vseh temnih stvareh, o vseh skrivnostih, ki jih stvari skrivajo v sebi... Po starih spomenikih je to zapisal pisar Ahmes.” Rokopis se imenuje “Ahmesov papirus”, oz papirus Rhind - po imenu Angleža, ki je našel in kupil ta papirus v Egiptu. Ahmesov papirus nudi rešitve za 84 problemov, ki vključujejo različne izračune, ki so morda potrebni v praksi.
Ohranjanje vaše zasebnosti je za nas pomembno. Iz tega razloga smo razvili Politiko zasebnosti, ki opisuje, kako uporabljamo in shranjujemo vaše podatke. Preglejte naše postopke varovanja zasebnosti in nam sporočite, če imate kakršna koli vprašanja.
Zbiranje in uporaba osebnih podatkov
Osebni podatki se nanašajo na podatke, ki jih je mogoče uporabiti za identifikacijo ali vzpostavitev stika z določeno osebo.
Kadar koli stopite v stik z nami, boste morda morali posredovati svoje osebne podatke.
Spodaj je nekaj primerov vrst osebnih podatkov, ki jih lahko zbiramo, in kako lahko te podatke uporabimo.
Katere osebne podatke zbiramo:
- Ko na spletnem mestu oddate prijavo, lahko zberemo različne podatke, vključno z vašim imenom, telefonsko številko, e-poštnim naslovom itd.
Kako uporabljamo vaše osebne podatke:
- Osebni podatki, ki jih zbiramo, nam omogočajo, da vas kontaktiramo z edinstvenimi ponudbami, promocijami in drugimi dogodki ter prihajajočimi dogodki.
- Občasno lahko uporabimo vaše osebne podatke za pošiljanje pomembnih obvestil in sporočil.
- Osebne podatke lahko uporabljamo tudi za interne namene, kot so izvajanje revizij, analize podatkov in različne raziskave, da bi izboljšali storitve, ki jih nudimo, in vam dali priporočila glede naših storitev.
- Če sodelujete v nagradni igri, tekmovanju ali podobni promociji, lahko podatke, ki nam jih posredujete, uporabimo za upravljanje takih programov.
Razkritje informacij tretjim osebam
Prejetih podatkov ne razkrivamo tretjim osebam.
Izjeme:
- Če je potrebno - v skladu z zakonom, sodnim postopkom, v sodnem postopku in/ali na podlagi javnih zahtev ali zahtev državnih organov na ozemlju Ruske federacije - za razkritje vaših osebnih podatkov. Podatke o vas lahko razkrijemo tudi, če ugotovimo, da je takšno razkritje potrebno ali primerno za varnostne namene, namene kazenskega pregona ali druge javno pomembne namene.
- V primeru reorganizacije, združitve ali prodaje lahko osebne podatke, ki jih zberemo, prenesemo na ustrezno naslednico tretje osebe.
Varstvo osebnih podatkov
Izvajamo previdnostne ukrepe – vključno z administrativnimi, tehničnimi in fizičnimi – za zaščito vaših osebnih podatkov pred izgubo, krajo in zlorabo ter nepooblaščenim dostopom, razkritjem, spreminjanjem in uničenjem.
Spoštovanje vaše zasebnosti na ravni podjetja
Da bi zagotovili varnost vaših osebnih podatkov, svojim zaposlenim sporočamo standarde zasebnosti in varnosti ter strogo uveljavljamo prakse glede zasebnosti.
Ministrstvo za izobraževanje in znanost Ruske federacije
Občinska proračunska izobraževalna ustanova
mesto Novosibirsk "Gimnazija št. 4"
Oddelek: matematika
RAZISKOVALNO DELO
na temo:
LASTNOSTI DVEH DOTIKALNIH KROGOV
Učenci 10. razreda:
Khaziakhmetov Radik Ildarovich
Zubarev Evgenij Vladimirovič
Nadzornik:
L.L. Barinova
Učiteljica matematike
Najvišja kvalifikacijska kategorija
§ 1. Uvod………..……………………………………………………………………………………3
§ 1.1 Relativni položaj dveh krogov ………………………………………………………3
§ 2 Lastnosti in njihovi dokazi……………………………………………………………………………….....….…4
§ 2.1 Lastnost 1……………………………………………………..…………………...….…4
§ 2.2 Lastnost 2………………………………………………………………………………………5
§ 2.3 Lastnost 3………………………………………………………………………………………6
§ 2.4 Lastnost 4……………………………………………………..………………………………6
§ 2.5 Lastnost 5…………………………………..……………………………………………8
§ 2.6 Lastnost 6…………………………………………………………………………………………9
§ 3 Naloge…………………………………………………..…………………………………..…11
Literatura………………………………………………………………………………………………….13
§ 1. Uvod
Veliko problemov, ki vključujejo dve tangentni krožnici, je mogoče rešiti bolj na kratko in preprosto s poznavanjem nekaterih lastnosti, ki bodo predstavljene v nadaljevanju.
Relativni položaj dveh krogov
Za začetek določimo možen relativni položaj obeh krogov. Lahko so 4 različni primeri.
1. Krogi se ne smejo sekati.
2. Preseči.

3. Dotaknite se ene točke na zunanji strani.

4. Dotaknite se ene točke znotraj.
§ 2. Lastnosti in njihovi dokazi
Pojdimo neposredno k dokazu lastnosti.
§ 2.1 Lastnost 1
Odseki med presečiščema tangent s krožnicami so med seboj enaki in enaki dvema geometrijskima srednjima polmeroma danih krožnic.

Dokaz 1. O 1 A 1 in O 2 B 1 – radija, narisana do stičnih točk.
2. О 1 А 1 ┴ А 1 В 1 , О2В1 ┴ А 1 В 1 → О 1 А 1 ║ О 2 В 1 (v skladu s točko 1).

- ▲O 1 O 2 D – pravokoten, ker О 2 D ┴ О 2 В 1
- O 1 O 2 = R + r, O 2 D = R – r

- Po Pitagorovem izreku A 1 B 1 = 2√Rr
(O 1 D 2 =(R+r) 2 -(R-r) 2 =R 2 +2Rr+r2-R 2 +2Rr-r 2 =√4Rr=2√Rr)
A 2 B 2 = 2√Rr (dokazano podobno)
1) V presečiščih tangent s krožnicami narišimo polmere.
2) Ti radiji bodo pravokotni na tangente in vzporedni drug z drugim.
3) Spustimo navpičnico iz središča manjšega kroga na polmer večjega kroga.
4) Hipotenuza nastalega pravokotnega trikotnika je enaka vsoti polmerov krogov. Krak je enak njuni razliki.
5) S pomočjo Pitagorovega izreka dobimo zahtevano razmerje.
§ 2.2 Lastnost 2
Presečišča ravne črte, ki sekajo tangentno točko krogov in ne ležijo v nobeni od njih s tangentami, delijo segmente zunanjih tangent, omejene s točkami dotikov, na polovico na dele, od katerih vsak je enaka geometrijski sredini polmerov teh krogov.

Dokaz 1.MS= MA 1 (kot tangentni segmenti)
2.MC = MV 1 (kot tangentni segmenti)
3.A 1 M = MV 1 = √Rr, A 2 N = NB 2 = √Rr (glede na 1. in 2. točko )

Izjave, uporabljene v dokazu Odseki tangente, narisani iz ene točke na določen krog, so enaki. To lastnost uporabimo za oba dana kroga.
§ 2.3 Lastnost 3
Dolžina odseka notranje tangente, sklenjene med zunanjima tangentama, je enaka dolžini odseka zunanje tangente med stičnima točkama in je enaka dvema geometričnima srednjima polmeroma danih krožnic.

Dokaz Ta sklep izhaja iz prejšnje lastnosti.
MN = MC + CN = 2MC = 2A 1 M = A 1 B 1 = 2√Rr

§ 2.4 Lastnost 4
Trikotnik, ki ga sestavljajo središča tangentnih krožnic in središče tangentnega odseka med polmeri, narisanimi na stične točke, je pravokoten. Razmerje njegovih krakov je enako kvocientu korenin polmerov teh krogov.

Dokaz 1.MO 1 je simetrala kota A 1 MS, MO 2 je simetrala kota B 1 MS, ker Središče kroga, včrtanega v kot, leži na simetrali tega kota.

2. Po točki 1 je РО 1 MS + РСМО 2 = 0,5(РА1МС + РСМВ 1) = 0,5p = p/2

3.РО 1 MO 2 – neposredno. MC je višina trikotnika O 1 MO 2, ker tangenta MN je pravokotna na polmere, narisane na stičišče → trikotnika O 1 MC in MO 2 C sta si podobna.

4.O 1 M / MO 2 = O 1 C / MC = r / √Rr = √r / R (podobno)
Izjave, uporabljene v dokazu 1) Središče kroga, včrtanega v kot, leži na simetrali tega kota. Kraki trikotnika so simetrale kotov.
2) Iz dejstva, da sta tako nastala kota enaka, ugotovimo, da je iskani kot pravi kot. Sklepamo, da je ta trikotnik res pravokoten.
3) Dokažemo podobnost trikotnikov, na katere višina (ker je tangenta pravokotna na polmere, narisane na stičišče) deli pravokotni trikotnik, in s podobnostjo dobimo zahtevano razmerje.
§ 2.5 Lastnost 5
Trikotnik, ki ga tvorita točka stika krožnic med seboj in presečišča krožnic s tangento, je pravokoten. Razmerje njegovih krakov je enako kvocientu korenin polmerov teh krogov.

Dokaz
- ▲A 1 MC in ▲SMV 1 sta enakokraka → ÐMA 1 C = ÐMSA 1 = α, ÐMV 1 C = ÐMSV 1 = β.

- 2α + 2β + RA 1 MC + RSMV 1 = 2p → 2α + 2β = 2p - (RA 1 MC + RSMV 1) = 2p - p = p, α + β = p/2

- Toda RA 1 SV 1 = α + β → RA 1 SV 1 – neposredno → RA 1 CO 2 = RASV 1 O 2 = p/2 – β = α

- ▲A 1 MC in ▲CO 2 B 1 sta podobna → A 1 C / SV 1 = MC / O 2 B 1 = √Rr / R = √r / R
Izjave, uporabljene v dokazu 1) Zapišemo vsoto kotov trikotnikov, pri čemer izkoristimo dejstvo, da so enakokraki. Enakokračnost trikotnikov dokažemo z lastnostjo enakosti tangentnih segmentov.
2) Ko tako zapišemo vsoto kotov, ugotovimo, da ima obravnavani trikotnik pravokoten, torej pravokoten. Prvi del trditve je dokazan.
3) S pomočjo podobnosti trikotnikov (za utemeljitev uporabimo znak podobnosti pri dveh kotih) poiščemo razmerje krakov pravokotnega trikotnika.
§ 2.6 Lastnost 6
Štirikotnik, ki ga tvorijo presečišča krožnic s tangento, je trapez, v katerega je mogoče vpisati krog.

Dokaz 1.▲A 1 RA 2 in ▲B 1 PB 2 sta enakokraka, ker A 1 P = RA 2 in B 1 P = PB 2 kot tangentna odseka → ▲A 1 RA 2 in ▲B 1 PB 2 – podobno.

2.A 1 A 2 ║ B 1 B 2, ker ustrezna kota, ki nastaneta v presečišču sekante A 1 B 1, sta enaka.

- MN – sredinska črta po lastnosti 2 → A 1 A 2 + B 1 B 2 = 2MN = 4√Rr

- A 1 B 1 + A 2 B 2 = 2√Rr + 2√Rr = 4√Rr = A 1 A 2 + B 1 B 2 → v trapezu A 2 A 1 B 1 B 2 je vsota osnov enaka na vsoto stranic, to pa je nujen in zadosten pogoj za obstoj včrtanega kroga.

Izjave, uporabljene v dokazu 1) Ponovno uporabimo lastnost tangentnih odsekov. Z njegovo pomočjo bomo dokazali enakokrake trikotnikov, ki jih tvorita presečišče tangent in stičišče.
2) Iz tega bo sledilo, da sta si ta trikotnika podobna in sta njuni osnovici vzporedni. Na podlagi tega sklepamo, da je ta štirikotnik trapez.
3) Z lastnostjo (2), ki smo jo dokazali prej, poiščemo srednjico trapeza. Enak je dvema geometrijskima srednjima polmeroma krogov. V nastalem trapezu je vsota osnov enaka vsoti stranic, to pa je nujen in zadosten pogoj za obstoj včrtanega kroga.
§ 3. Težave
Oglejmo si praktičen primer, kako lahko poenostavite rešitev problema z uporabo zgoraj opisanih lastnosti.
Problem 1
V trikotnik ABC je stranica AC = 15 cm včrtana. Drugi krog se dotika prvega ter stranic AB in BC. Na strani AB je izbrana točka F, na strani BC pa točka M, tako da je odsek FM skupna tangenta na krožnici. Poiščite razmerje ploščin trikotnika BFM in štirikotnika AFMC, če je FM 4 cm in je točka M dvakrat bolj oddaljena od središča enega kroga kot od središča drugega.
podano: FM-totalni tangens AC=15cm FM=4cm O 2 M=2О 1 M
Poiščite S BFM /S AFMC

rešitev:
1)FM=2√Rr,O 1 M/O 2 M=√r/R
2)2√Rr=4, √r/R=0,5 →r=1,R=4; PQ=FM=4
3)▲BO 1 P in ▲BO 2 Q sta podobna → BP/BQ=O 1 P/O 2 Q, BP/(BP+PQ)=r/R,BP/(BP+4)=0,25;BP = 4/3
4)FM+BP=16/3, S FBM =r*P FBM =1*(16/3)=16/3; AC+BQ=15+4/3+4=61/3
5)S ABC =R*P ABC =4*(61/3)=244/3 → S BFM /S AFMC =(16/3):(244/3)=4/61
 Problem 2
Problem 2
Enakokrakemu trikotniku ABC sta vpisani dve tangentni krožnici s skupno točko D in skupno tangento FK, ki potekata skozi to točko. Poiščite razdaljo med središči teh krogov, če je osnova trikotnika AC = 9 cm in je odsek stranice trikotnika, ki je zaprt med stičnima točkama krogov, 4 cm.
podano: ABC – enakokraki trikotnik; FK – skupna tangenta včrtanih krožnic. AC = 9 cm; SV = 4 cm

rešitev:
Naj se premici AB in CD sekata v točki O. Potem je OA = OD, OB = OC, torej CD = = AB = 2√Rr
Točki O 1 in O 2 ležita na simetrali kota AOD. Simetrala enakokrakega trikotnika AOD je njegova nadmorska višina, torej AD ┴ O 1 O 2 in BC ┴ O 1 O 2, kar pomeni
AD ║ BC in ABCD – enakokraki trapez.
Odsek MN je njegova srednja črta, torej AD + BC = 2MN = 2AB = AB + CD
Zato lahko v ta trapez vpišemo krog.
Naj bo AP višina trapeza, pravokotna trikotnika ARB in O 1 FO 2 sta si podobna, zato je AP/O 1 F = AB/O 1 O 2.
Od tod to ugotovimo 
Reference
- Dodatek k časopisu "Prvi september" "Matematika" št. 43, 2003
- Enotni državni izpit 2010. Matematika. Naloga C4. Gordin R.K.
 Tajna ekspedicija OGPU v skrivnostno državo Shambhala
Tajna ekspedicija OGPU v skrivnostno državo Shambhala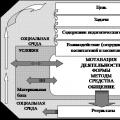 Znanstvena elektronska knjižnica Pedagoški proces predstavlja
Znanstvena elektronska knjižnica Pedagoški proces predstavlja Predstavitev na temo "A.A. Blok". Predstavitev na temo "Alexander Alexandrovich Blok" Družina in sorodniki
Predstavitev na temo "A.A. Blok". Predstavitev na temo "Alexander Alexandrovich Blok" Družina in sorodniki