Kako iskati asimptote funkcije. Kako najti asimptote grafa funkcije? Kaj to pomeni
Koliko asimptot ima lahko graf funkcije?
Ne ena, ena, dve, tri,... ali neskončno veliko. Za primere ne bomo šli daleč, spomnimo se osnovnih funkcij. Parabola, kubična parabola in sinusni val sploh nimajo asimptot. Graf eksponentne logaritemske funkcije ima eno samo asimptoto. Arkustangens in arkotangens imata dva, tangens in kotangens pa neskončno veliko. Ni neobičajno, da ima graf vodoravne in navpične asimptote. Hiperbola, vedno te bom imel rad.
Kaj pomeni najti asimptote grafa funkcije?
To pomeni ugotoviti njihove enačbe in risati ravne črte, če problem to zahteva. Postopek vključuje iskanje meja funkcije.
Navpične asimptote grafa funkcije
Navpična asimptota grafa se praviloma nahaja na točki neskončne diskontinuitete funkcije. Preprosto je: če na neki točki funkcija trpi za neskončno diskontinuiteto, potem je ravna črta, določena z enačbo, navpična asimptota grafa.
Opomba: Upoštevajte, da se vnos uporablja za sklicevanje na dva popolnoma različna koncepta. Ali je implicirana točka ali enačba črte, je odvisno od konteksta.
Tako je za ugotovitev prisotnosti navpične asimptote v točki dovolj pokazati, da je vsaj ena od enostranskih meja neskončna. Najpogosteje je to točka, kjer je imenovalec funkcije enak nič. V bistvu smo navpične asimptote že našli v zadnjih primerih lekcije o zveznosti funkcije. Toda v nekaterih primerih obstaja samo ena enostranska meja, in če je neskončna, potem spet - ljubite in dajete prednost navpični asimptoti. Najenostavnejša ponazoritev: in ordinatna os.
Iz zgoraj navedenega sledi tudi očitno dejstvo: če je funkcija zvezna, potem ni navpičnih asimptot. Iz nekega razloga mi je na misel prišla parabola. Saj res, kam lahko tukaj »zatakneš« ravno črto? ...ja... razumem... sledilci strica Freuda so postali histerični =)
Obratna trditev je na splošno napačna: funkcija na primer ni definirana na celotni številski premici, ampak je popolnoma brez asimptot.
Nagnjene asimptote grafa funkcije
Poševne (kot poseben primer - vodoravne) asimptote lahko narišemo, če argument funkcije teži k "plus neskončnosti" ali k "minus neskončnosti". Zato graf funkcije ne more imeti več kot 2 nagnjenih asimptot. Na primer, graf eksponentne funkcije ima eno vodoravno asimptoto pri , graf arktangensa pri ima dve takšni asimptoti, in to različni.
Ko se graf na obeh mestih približa eni poševni asimptoti, je običajno združiti "neskončnosti" pod enim vnosom. Na primer, ...pravilno ste uganili: .
Asimptota grafa funkcije y = f(x) je premica, ki ima to lastnost, da se razdalja od točke (x, f(x)) do te premice nagiba k nič, ko se točka grafa premakne za nedoločen čas od izhodišča.
Na sliki 3.10. podani so grafični primeri navpično, vodoravno in nagnjen asimptota.
Iskanje asimptot grafa temelji na naslednjih treh izrekih.
Izrek o navpični asimptoti. Naj bo funkcija y = f(x) definirana v neki okolici točke x 0 (mogoče brez te točke same) in je vsaj ena od enostranskih limitov funkcije enaka neskončnosti, tj. Potem je premica x = x 0 navpična asimptota grafa funkcije y = f(x).
Očitno je, da premica x = x 0 ne more biti navpična asimptota, če je funkcija zvezna v točki x 0, saj v tem primeru ![]() . Posledično je treba navpične asimptote iskati na diskontinuitetnih točkah funkcije ali na koncih njene definicijske domene.
. Posledično je treba navpične asimptote iskati na diskontinuitetnih točkah funkcije ali na koncih njene definicijske domene.
Izrek o vodoravni asimptoti. Naj bo funkcija y = f(x) definirana za dovolj velik x in obstaja končna meja funkcije. Potem je premica y = b vodoravna asimptota grafa funkcije.
Komentiraj. Če je samo ena od mej končna, potem ima funkcija temu primerno levičar oz desnostranski horizontalna asimptota.
V primeru, da ima lahko funkcija poševno asimptoto.
Izrek o poševni asimptoti. Naj bo funkcija y = f(x) definirana za dovolj velik x in obstajajo končne meje ![]() . Potem je premica y = kx + b poševna asimptota grafa funkcije.
. Potem je premica y = kx + b poševna asimptota grafa funkcije.
Nobenega dokaza.
Poševna asimptota, tako kot vodoravna, je lahko desno ali levosučna, če osnova ustreznih mej vsebuje neskončnost določenega predznaka.
Preučevanje funkcij in izdelava njihovih grafov običajno vključuje naslednje korake:
1. Poišči domeno definicije funkcije.
2. Preglejte funkcijo za sodo-liho.
3. Poiščite navpične asimptote s preučevanjem diskontinuitetnih točk in obnašanja funkcije na mejah definicijskega področja, če so končne.
4. Poiščite vodoravne ali poševne asimptote s preučevanjem obnašanja funkcije v neskončnosti.
5. Poiščite ekstreme in intervale monotonosti funkcije.
6. Poiščite intervale konveksnosti funkcije in prevojne točke.
7. Poiščite presečišča s koordinatnimi osemi in po možnosti nekaj dodatnih točk, ki pojasnjujejo graf.
Funkcijski diferencial
Dokaže se lahko, da če ima funkcija mejo, ki je enaka končnemu številu za določeno osnovo, jo lahko predstavimo kot vsoto tega števila in neskončno majhne vrednosti za isto osnovo (in obratno): .
Uporabimo ta izrek za diferenciabilno funkcijo: .
Tako je prirastek funkcije Dу sestavljen iz dveh členov: 1) linearen glede na Dx, tj. f `(x)Dх; 2) nelinearna glede na Dx, tj. a(Dx)Dх. Hkrati pa od ![]() , ta drugi člen predstavlja neskončno malo več visokega reda kot Dx (ko se Dx nagiba k ničli, se nagiba k ničli še hitreje).
, ta drugi člen predstavlja neskončno malo več visokega reda kot Dx (ko se Dx nagiba k ničli, se nagiba k ničli še hitreje).
Diferencial funkcija je glavni, linearni glede na Dx del prirastka funkcije, ki je enak zmnožku odvoda in prirastka neodvisne spremenljivke dy = f `(x)Dx.
Poiščimo diferencial funkcije y = x.
Ker je dy = f `(x)Dх = x`Dх = Dх, potem je dx = Dх, tj. diferencial neodvisne spremenljivke je enak prirastku te spremenljivke.
Zato lahko formulo za diferencial funkcije zapišemo kot dy = f `(x)dх. Zato je eden od zapisov za derivat ulomek dy/dx.

Geometrijski pomen ilustriran diferencial
Slika 3.11. Vzemimo poljubno točko M(x, y) na grafu funkcije y = f(x). Dajmo argumentu x prirastek Dx. Potem bo funkcija y = f(x) prejela prirastek Dy = f(x + Dх) - f(x). Na graf funkcije v točki M narišimo tangento, ki s pozitivno smerjo abscisne osi tvori kot a, t.j. f `(x) = tan a. Od pravokotni trikotnik MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.
Tako je diferencial funkcije prirastek v ordinati tangente, narisane na graf funkcije v dani točki, ko x prejme prirastek Dx.
Lastnosti diferenciala so v bistvu enake lastnostim derivata:
3. d(u ± v) = du ± dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du - u dv)/v 2.
Vendar pa obstaja pomembna lastnina diferencial funkcije, ki ga njen derivat nima, je invariantnost diferencialne oblike.
Iz definicije diferenciala za funkcijo y = f(x) je diferencial dy = f `(x)dх. Če je ta funkcija y kompleksna, tj. y = f(u), kjer je u = j(x), potem je y = f in f `(x) = f `(u)*u`. Potem je dy = f `(u)*u`dх. Ampak za funkcijo
u = j(x) diferencial du = u`dх. Zato je dy = f `(u)*du.
S primerjavo enakosti dy = f `(x)dх in dy = f `(u)*du se prepričamo, da se diferencialna formula ne spremeni, če namesto funkcije neodvisne spremenljivke x upoštevamo funkcijo odvisna spremenljivka u. Ta lastnost diferenciala se imenuje invariantnost (tj. nespremenljivost) oblike (ali formule) diferenciala.
Še vedno pa obstaja razlika v teh dveh formulah: v prvi od njiju je razlika neodvisne spremenljivke enaka prirastku te spremenljivke, tj. dx = Dx, in drugič, diferencial funkcije du je le linearni del prirastka te funkcije Du in samo za majhne Dх du » Du.
Na voljo bodo tudi naloge za neodvisna odločitev, na katerega si lahko ogledate odgovore.
Koncept asimptote
Če najprej zgradite asimptote krivulje, potem v mnogih primerih postane konstrukcija grafa funkcije lažja.
Usoda asimptote je polna tragedije. Predstavljajte si, kako je: vse življenje se premikate naravnost proti svojemu cenjenemu cilju, se mu čim bolj približate, a ga nikoli ne dosežete. Na primer, poskušajte povezati svoje življenjska pot s potjo želene osebe, se mu na neki točki skoraj približati, a se ga niti ne dotakniti. Ali pa si prizadevajte zaslužiti milijardo, a pred dosego tega cilja in vpisom v Guinnessovo knjigo rekordov za vaš primer manjkajo stotinke centa. In podobno. Tako je tudi z asimptoto: nenehno si prizadeva doseči krivuljo grafa funkcije, se ji približa na najmanjšo možno razdaljo, a se je nikoli ne dotakne.
Definicija 1. Asimptote so tiste premice, ki se jim graf funkcije približa poljubno blizu, ko spremenljivka teži k plus neskončnosti ali minus neskončnosti.
Definicija 2. Ravna črta se imenuje asimptota grafa funkcije, če je razdalja od spremenljive točke M graf funkcije do te premice teži k ničli, ko se točka odmika za nedoločen čas M od izhodišča vzdolž katere koli veje funkcijskega grafa.
Obstajajo tri vrste asimptot: navpične, vodoravne in poševne.
Vertikalne asimptote
Prva stvar, ki jo morate vedeti o navpičnih asimptotah, je, da so vzporedne z osjo Oj .
Opredelitev. Naravnost x = a je navpična asimptota grafa funkcije , če točka x = a je točka diskontinuitete druge vrste za to funkcijo.
Iz definicije sledi, da ravna črta x = a je navpična asimptota grafa funkcije f(x), če je izpolnjen vsaj eden od pogojev:
V tem primeru funkcija f(x) sploh ni mogoče definirati oziroma kdaj x ≥ a in x ≤ a .
komentar:

Primer 1. Graf funkcije l=ln x ima navpično asimptoto x= 0 (tj. sovpada z osjo Oj) na meji definicijskega področja, ker je limita funkcije, ko x teži k ničli z desne, enaka minus neskončnosti:
(slika zgoraj).
sami in si nato oglejte rešitve
Primer 2. Poiščite asimptote grafa funkcije.
Primer 3. Poiščite asimptote grafa funkcije
Horizontalne asimptote
Prva stvar, ki jo morate vedeti o vodoravnih asimptotah, je, da so vzporedne z osjo Ox .
Če je (meja funkcije, ko se argument nagiba k plus ali minus neskončnosti, enaka določeni vrednosti b), to l = b – horizontalna asimptota ukrivljen l = f(x ) (desno, ko X teži k plus neskončnosti, levo, ko X teži k minus neskončnosti, in dvostransko, če so meje, ko X teži k plus ali minus neskončnosti, enake).

Primer 5. Graf funkcije
pri a> 1 ima levo vodoravno asimpototo l= 0 (tj. sovpada z osjo Ox), ker je meja funkcije, ko se "x" nagiba k minus neskončnosti, nič:
Krivulja nima desne horizontalne asimptote, ker je meja funkcije, ko se "x" nagiba k plus neskončnosti, enaka neskončnosti:
Poševne asimptote
Navpične in vodoravne asimptote, ki smo jih pregledali zgoraj, so vzporedne s koordinatnimi osemi, zato smo za njihovo konstrukcijo potrebovali le določeno število - točko na osi abscise ali ordinate, skozi katero poteka asimptota. Za poševno asimptoto je potreben večji naklon k, ki prikazuje kot naklona črte, in prosti člen b, ki prikazuje, koliko je črta nad ali pod izhodiščem. Tisti, ki niso pozabili analitične geometrije in iz nje enačb premice, bodo opazili, da za poševno asimptoto ugotovijo enačba premice z naklonom. Obstoj poševne asimptote določa naslednji izrek, na podlagi katerega najdemo pravkar omenjene koeficiente.
Izrek. Za izdelavo krivulje l = f(x) imel asimptoto l = kx + b , je nujno in zadostno, da obstajajo končne meje k in b obravnavane funkcije, ko se spremenljivka nagiba x do plus neskončnosti in minus neskončnosti:
![]() (1)
(1)
![]() (2)
(2)
Številke, ugotovljene na ta način k in b in sta koeficienta poševne asimptote.
V prvem primeru (ko x teži k plus neskončnosti) dobimo desno nagnjeno asimptoto, v drugem primeru (ko x teži k minus neskončnosti) dobimo levo poševno asimptoto. Desna poševna asimptota je prikazana na sl. spodaj.

Pri iskanju enačbe za poševno asimptoto je treba upoštevati težnjo X k plus in minus neskončnosti. Za nekatere funkcije, na primer frakcijske racionalne, te meje sovpadajo, vendar so za mnoge funkcije te meje različne in lahko obstaja samo ena od njih.
Če meje sovpadajo in x teži k plus neskončnosti in minus neskončnosti, je ravna črta l = kx + b je dvostranska asimptota krivulje.
Če je vsaj ena od mej, ki določajo asimptoto l = kx + b , ne obstaja, potem graf funkcije nima poševne asimptote (ima pa lahko navpično).
Preprosto je videti, da vodoravna asimptota l = b je poseben primer poševnega l = kx + b pri k = 0 .
Torej, če ima krivulja v kateri koli smeri vodoravno asimptoto, potem v tej smeri ni nagnjene in obratno.
Primer 6. Poiščite asimptote grafa funkcije
rešitev. Funkcija je definirana na celotni številski premici razen x= 0, tj.
Zato na prelomni točki x= 0 ima lahko krivulja navpično asimptoto. Dejansko je meja funkcije, ko x teži k ničli z leve, enaka plus neskončnosti:


torej x= 0 – navpična asimptota grafa te funkcije.
Graf te funkcije nima horizontalne asimptote, saj je meja funkcije, ko x teži k plus neskončnosti, enaka plus neskončnosti:
![]()
Ugotovimo prisotnost poševne asimptote:

Ima končne meje k= 2 in b= 0. Naravnost l = 2x je dvosmerna poševna asimptota grafa te funkcije (slika v primeru).
Primer 7. Poiščite asimptote grafa funkcije
rešitev. Funkcija ima eno prekinitveno točko x= −1 . Izračunajmo enostranske meje in določimo vrsto diskontinuitete:
Zaključek: x= −1 je točka diskontinuitete druge vrste, torej premica x= −1 je navpična asimptota grafa te funkcije.
Iščemo poševne asimptote. Ker je ta funkcija frakcijsko-racionalna, limiti pri in pri volji sovpadata. Tako najdemo koeficiente za zamenjavo ravne črte - poševne asimptote v enačbo:


Če nadomestimo najdene koeficiente v enačbo ravne črte s koeficientom naklona, dobimo enačbo poševne asimptote:
l = −3x + 5 .
Na sliki je graf funkcije označen z bordo barvo, asimptote pa s črno.
Primer 8. Poiščite asimptote grafa funkcije
rešitev. Ker je ta funkcija zvezna, njen graf nima navpičnih asimptot. Iščemo poševne asimptote:
 .
.
Tako ima graf te funkcije asimptoto l= 0 pri in nima asiptote pri .

Primer 9. Poiščite asimptote grafa funkcije
rešitev. Najprej iščemo navpične asimptote. Da bi to naredili, poiščemo domeno definicije funkcije. Funkcija je definirana, ko sta neenakost in . Predznak spremenljivke x se ujema z znakom. Zato upoštevajte ekvivalentno neenakost. Iz tega dobimo domeno definicije funkcije: ![]() . Navpična asimptota je lahko samo na meji domene definicije funkcije. Ampak x= 0 ne more biti navpična asimptota, ker je funkcija definirana pri x = 0
.
. Navpična asimptota je lahko samo na meji domene definicije funkcije. Ampak x= 0 ne more biti navpična asimptota, ker je funkcija definirana pri x = 0
.
Upoštevajte desno mejo pri (leve meje ni):
![]() .
.
Pika x= 2 je točka diskontinuitete druge vrste, torej premica x= 2 - navpična asimptota grafa te funkcije.
Iščemo poševne asimptote:

Torej, l = x+ 1 - poševna asimptota grafa te funkcije pri . Iščemo poševno asimptoto pri:
Torej, l = −x − 1 - poševna asimptota pri .

Primer 10. Poiščite asimptote grafa funkcije
rešitev. Funkcija ima domeno definicije ![]() . Ker je navpična asimptota grafa te funkcije lahko samo na meji definicijskega področja, najdemo enostranske limite funkcije pri .
. Ker je navpična asimptota grafa te funkcije lahko samo na meji definicijskega področja, najdemo enostranske limite funkcije pri .
Asimptote grafa funkcije
Duh asimptote je dolgo taval po spletnem mestu, da bi se končno udejanjil v ločenem članku in posebej razveselil zmedene bralce popolna študija funkcije. Iskanje asimptot grafa je eden redkih delov navedene naloge, ki je v šolskem tečaju obravnavan le pregledno, saj se dogajanje vrti okoli izračuna meje delovanja, vendar še vedno spadajo v višjo matematiko. Za obiskovalce, ki se malo razumejo v matematični analizi, mislim, da je namig jasen ;-) ...stop, stop, kam greš? Omejitve- enostavno je!
Na primere asimptot smo naleteli takoj v prvi lekciji o grafi elementarnih funkcij, tema pa je zdaj deležna podrobne obravnave.
Kaj je torej asimptota?
Predstavljajte si spremenljiva točka, ki “potuje” po grafu funkcije. Asimptota je naravnost, do katerega za nedoločen čas blizu graf funkcije se približuje, ko se njena spremenljiva točka premika v neskončnost.
Opomba : Definicija je smiselna, če potrebujete formulacijo v računskem zapisu, si oglejte učbenik.
Na ravnini so asimptote razvrščene glede na njihovo naravno lokacijo:
1) Vertikalne asimptote, ki so podane z enačbo oblike , kjer je "alfa". realno število. Ljudski predstavnik sam določi ordinatno os,
z rahlim občutkom slabosti se spomnimo hiperbole.
2) Poševne asimptote tradicionalno napisano enačba premice s kotnim koeficientom. Včasih je poseben primer označen kot ločena skupina - horizontalne asimptote. Na primer, ista hiperbola z asimptoto.
Gremo hitro, zadenimo temo s kratkim rafalom iz mitraljeza:
Koliko asimptot ima lahko graf funkcije?
Ne ena, ena, dve, tri,... ali neskončno veliko. Za primere ne bomo šli daleč, spomnimo se elementarne funkcije. Parabola, kubična parabola in sinusni val sploh nimajo asimptote. Graf eksponentne logaritemske funkcije ima eno samo asimptoto. Arktangens in arkotangens imata dva, tangens in kotangens pa neskončno veliko. Ni neobičajno, da ima graf vodoravne in navpične asimptote. Hiperbola, vedno te bom imel rad.
Kaj to pomeni?
Navpične asimptote grafa funkcije
Običajno se nahaja navpična asimptota grafa na točki neskončne diskontinuitete funkcije. Preprosto je: če na neki točki funkcija trpi za neskončno diskontinuiteto, potem je ravna črta, določena z enačbo, navpična asimptota grafa.
Opomba : Upoštevajte, da se vnos uporablja za sklicevanje na dva popolnoma različna koncepta. Ali je implicirana točka ali enačba črte, je odvisno od konteksta.
Tako je za ugotovitev prisotnosti navpične asimptote v točki dovolj pokazati to vsaj enega iz enostranskih meja ![]() neskončno. Najpogosteje je to točka, kjer je imenovalec funkcije enak nič. V bistvu smo navpične asimptote že našli v zadnjih primerih lekcije o zveznosti funkcije. Toda v nekaterih primerih obstaja samo ena enostranska meja, in če je neskončna, potem spet - ljubite in dajete prednost navpični asimptoti. Najenostavnejša ilustracija: in ordinatna os (glej. Grafi in lastnosti elementarnih funkcij).
neskončno. Najpogosteje je to točka, kjer je imenovalec funkcije enak nič. V bistvu smo navpične asimptote že našli v zadnjih primerih lekcije o zveznosti funkcije. Toda v nekaterih primerih obstaja samo ena enostranska meja, in če je neskončna, potem spet - ljubite in dajete prednost navpični asimptoti. Najenostavnejša ilustracija: in ordinatna os (glej. Grafi in lastnosti elementarnih funkcij).
Iz zgoraj navedenega sledi tudi očitno dejstvo: če je funkcija neprekinjeno vključena, potem ni navpičnih asimptot. Iz nekega razloga mi je na misel prišla parabola. Saj res, kam lahko tukaj »nalepiš« ravno črto? ...ja... razumem... sledilci strica Freuda so postali histerični =)
Obratna trditev je na splošno napačna: funkcija na primer ni definirana na celotni številski premici, ampak je popolnoma brez asimptot.
Nagnjene asimptote grafa funkcije
Poševne (kot poseben primer - vodoravne) asimptote lahko narišemo, če argument funkcije teži k "plus neskončnosti" ali k "minus neskončnosti". zato graf funkcije ne sme imeti več kot dveh poševnih asimptot. Na primer, graf eksponentne funkcije ima eno vodoravno asimptoto pri , graf arktangensa pri ima dve takšni asimptoti, in to različni.
Ko se graf na obeh mestih približa eni poševni asimptoti, so »neskončnosti« običajno združene pod enim vnosom. Na primer, ...pravilno ste uganili: .
Splošno pravilo:
Če sta dva dokončno omejitev ![]() , potem je premica poševna asimptota grafa funkcije pri . če vsaj enega naštetih limit neskončno, potem ni poševne asimptote.
, potem je premica poševna asimptota grafa funkcije pri . če vsaj enega naštetih limit neskončno, potem ni poševne asimptote.
Opomba : formule ostanejo veljavne, če se "x" nagiba le k "plus neskončnosti" ali samo k "minus neskončnosti".
Pokažimo, da parabola nima poševnih asimptot: ![]()
Limita je neskončna, kar pomeni, da ni poševne asimptote. Upoštevajte, da pri iskanju meje ![]() potreba je odpadla, saj je odgovor že prejet.
potreba je odpadla, saj je odgovor že prejet.
Opomba
: Če imate (ali boste imeli) težave z razumevanjem znakov plus-minus, minus-plus, glejte pomoč na začetku lekcije
na infinitezimalnih funkcijah, kjer sem vam povedal, kako pravilno razlagati te znake.
Očitno je za vsak kvadrat, kubična funkcija, tudi polinom 4. in višjih stopenj nima poševnih asimptot.
Sedaj pa se prepričajmo, da tudi graf nima poševne asimptote. Za razkrivanje negotovosti uporabljamo L'Hopitalovo pravilo:
, kar je bilo treba preveriti.
Ko funkcija raste v nedogled, pa ni premice, ki bi se ji njen graf približal neskončno blizu.
Preidimo na praktični del lekcije:
Kako najti asimptote grafa funkcije?
Točno tako je formuliran tipična naloga, in vključuje iskanje VSEH asimptot grafa (navpično, nagnjeno/vodoravno). Čeprav, če smo bolj natančni pri postavljanju vprašanja, govorimo o raziskavah prisotnosti asimptot (navsezadnje jih morda sploh ni). Začnimo z nečim preprostim:
Primer 1
Poiščite asimptote grafa funkcije
rešitev Primerno ga je razdeliti na dve točki:
1) Najprej preverimo, ali obstajajo navpične asimptote. Imenovalec gre na nič pri , in takoj je jasno, da na tej točki trpi funkcija neskončna vrzel, premica, podana z enačbo, pa je navpična asimptota grafa funkcije. Toda preden naredite tak sklep, je treba najti enostranske meje: 
Opozarjam vas na tehniko izračunavanja, na katero sem se podobno osredotočil v članku Kontinuiteta delovanja. Prelomne točke. V izrazu pod mejnim znakom zamenjamo . V števniku ni nič zanimivega:
.
Toda v imenovalcu se izkaže infinitezimalno negativno število:
, določa usodo meje.
Leva meja je neskončna in načeloma je že mogoče soditi o prisotnosti navpične asimptote. Toda enostranske omejitve niso potrebne le za to - POMAGAJO RAZUMETI KAKO poiščite graf funkcije in ga zgradite PRAVILNO. Zato moramo izračunati tudi desno mejo: 
Zaključek: enostranske meje so neskončne, kar pomeni, da je premica navpična asimptota grafa funkcije pri .
Prva meja končno, kar pomeni, da je treba "nadaljevati pogovor" in najti drugo mejo:
Tudi druga meja končno.
Tako je naša asimptota:
Zaključek: premica, podana z enačbo, je vodoravna asimptota grafa funkcije pri .
Da bi našli horizontalno asimptoto
lahko uporabite poenostavljeno formulo:
Če obstaja končno meja, potem je premica horizontalna asimptota grafa funkcije pri .
Zlahka je videti, da sta števec in imenovalec funkcije isti vrstni red rasti, kar pomeni, da bo iskana meja končna: 
Odgovori:
Glede na stanje vam ni treba dokončati risbe, a če v polnem teku študija funkcije, nato na osnutku takoj naredimo skico: 
Na podlagi treh najdenih mej poskusite sami ugotoviti, kako bi se lahko nahajal graf funkcije. Je sploh težko? Poiščite 5-6-7-8 točk in jih označite na risbi. Vendar pa je graf te funkcije zgrajen z uporabo transformacije grafa elementarne funkcije, in bralci, ki so skrbno preučili 21. primer zgornjega članka, zlahka ugibajo, za kakšno krivuljo gre.
Primer 2
Poiščite asimptote grafa funkcije
To je primer, ki ga morate rešiti sami. Naj vas spomnim, da je proces priročno razdeljen na dve točki - navpične asimptote in poševne asimptote. V vzorčni rešitvi se vodoravna asimptota najde po poenostavljeni shemi.
V praksi se najpogosteje srečujemo z delno-racionalnimi funkcijami in po treningu na hiperbolah bomo nalogo zapletli:
Primer 3
Poiščite asimptote grafa funkcije ![]()
rešitev: En, dva in končano:
1) Navpične asimptote se nahajajo na točkah neskončne diskontinuitete, zato morate preveriti, ali gre imenovalec na nič. Odločimo se kvadratna enačba:![]()
Diskriminanta je pozitivna, zato ima enačba dva realna korena, delo pa se znatno poveča =) 
Za nadaljnje iskanje enostranskih mej je priročno faktorizirati kvadratni trinom:
(za kompakten zapis je bil "minus" vključen v prvi oklepaj). Za varnost ga preverimo tako, da miselno ali na osnutku odpremo oklepaje.
Prepišimo funkcijo v obliki ![]()
Poiščimo enostranske omejitve na točki: 
In pri bistvu: 
Tako so ravne črte navpične asimptote grafa zadevne funkcije.
2) Če pogledate funkcijo ![]() , potem je povsem očitno, da bo limita končna in imamo horizontalno asimptoto. Pokažimo njegovo prisotnost na kratek način:
, potem je povsem očitno, da bo limita končna in imamo horizontalno asimptoto. Pokažimo njegovo prisotnost na kratek način: ![]()
Tako je premica (abscisna os) vodoravna asimptota grafa te funkcije.
Odgovori:
Najdene limite in asimptote nudijo veliko informacij o grafu funkcije. Poskusite si mentalno predstavljati risbo ob upoštevanju naslednjih dejstev: 
Na osnutek skicirajte svojo različico grafa.
Seveda najdene meje ne določajo jasno videza grafa in lahko naredite napako, vendar vam bo vaja sama pri tem v neprecenljivo pomoč. študija celotne funkcije. Pravilna slika je na koncu lekcije.
Primer 4
Poiščite asimptote grafa funkcije
Primer 5
Poiščite asimptote grafa funkcije ![]()
To so naloge za samostojno reševanje. Oba grafa imata ponovno vodoravne asimptote, ki jih takoj zaznamo z naslednjimi značilnostmi: v primeru 4 red rasti imenovalec več, kot vrstni red rasti števca, v primeru 5 pa števca in imenovalca isti vrstni red rasti. V vzorčni rešitvi se prva funkcija preuči glede prisotnosti poševnih asimptot v celoti, druga pa skozi mejo.
Horizontalne asimptote so po mojem subjektivnem vtisu opazno pogostejše od tistih, ki so »resnično nagnjene«. Dolgo pričakovan splošni primer:
Primer 6
Poiščite asimptote grafa funkcije ![]()
rešitev: klasika žanra:
1) Ker je imenovalec pozitiven, potem je funkcija neprekinjeno vzdolž celotne številske premice in ni navpičnih asimptot. ...Je to dobro? Ni prava beseda - odlično! Točka št. 1 je zaprta.
2) Preverimo prisotnost poševnih asimptot:
Prva meja končno, torej gremo naprej. Med izračunom druge omejitve odpraviti negotovost "neskončnost minus neskončnost" Izraz spravimo na skupni imenovalec: 
Tudi druga meja končno Zato ima graf zadevne funkcije poševno asimptoto:
Zaključek:
Tako, ko je graf funkcije ![]() neskončno blizu se približuje ravni črti:
neskončno blizu se približuje ravni črti: 
Upoštevajte, da seka svojo poševno asimptoto v izvoru in takšne presečišča so povsem sprejemljiva - pomembno je, da je v neskončnosti "vse normalno" (pravzaprav tukaj govorimo o asimptotah).
Primer 7
Poiščite asimptote grafa funkcije
rešitev: Ni kaj posebnega za komentirati, zato bom narisal približen primer čiste rešitve:
1) Navpične asimptote. Raziščimo bistvo. 
Ravna črta je navpična asimptota za graf pri .
2) Poševne asimptote: 
Ravna črta je poševna asimptota za graf pri .
Odgovori: ![]()
Najdene enostranske meje in asimptote nam omogočajo, da z veliko zanesljivostjo napovemo, kako izgleda graf te funkcije. Pravilno risanje na koncu lekcije.
Primer 8
Poiščite asimptote grafa funkcije
To je primer neodvisne rešitve; zaradi lažjega izračuna nekaterih omejitev lahko števec delite z imenovalcem na člen. Še enkrat, ko analizirate svoje rezultate, poskusite narisati graf te funkcije.
Očitno so lastniki "pravih" poševnih asimptot njihovi grafi ulomke racionalne funkcije, ki imajo višjo stopnjo števnika še enega najvišja stopnja imenovalca. Če je več, ne bo poševne asimptote (na primer ).
Toda v življenju se dogajajo drugi čudeži:
Primer 9
![]()
Primer 11
Preglejte graf funkcije glede prisotnosti asimptot
rešitev: to je očitno ![]() , zato upoštevamo samo desno polravnino, kjer je graf funkcije.
, zato upoštevamo samo desno polravnino, kjer je graf funkcije.
Tako je premica (ordinatna os) navpična asimptota za graf funkcije pri .
2) Študijo poševne asimptote je mogoče izvesti po celotni shemi, vendar v članku L'Hopitalova pravila to smo ugotovili linearna funkcija višji vrstni red rasti kot logaritemski, torej: ![]() (Glej 1. primer iste lekcije).
(Glej 1. primer iste lekcije).
Sklep: os x je vodoravna asimptota grafa funkcije pri .
Odgovori:
, Če ;
, Če .
Risba za jasnost: 
Zanimivo je, da na videz podobna funkcija sploh nima asimptot (kdor želi, lahko to preveri).
Dva zadnja primera za samostojno učenje:
Primer 12
Preglejte graf funkcije glede prisotnosti asimptot ![]()
Rešitev lahko priročno razdelimo na dve točki:
1) Najprej preverimo, ali obstajajo navpične asimptote. Imenovalec gre na nič pri in takoj je jasno, da je na tej točki funkcija neskončno diskontinuirana, premica, ki jo določa enačba, pa je navpična asimptota grafa funkcije. Toda preden naredite tak sklep, je treba najti enostranske meje:

Opozarjam vas na tehniko računanja, ki sem se ji podobno posvetil v članku Zveznost funkcije. Prelomne točke. V izrazu pod mejnim znakom nadomestimo "X". V števniku ni nič zanimivega:
Toda imenovalec povzroči infinitezimalno negativno število:
Določa usodo meje.
Leva meja je neskončna in načeloma je že mogoče soditi o prisotnosti navpične asimptote. Toda enostranske omejitve niso potrebne samo za to - POMAGAJO RAZUMETI, KAKO se nahaja graf funkcije in ga PRAVILNO zgraditi. Zato moramo izračunati tudi desno mejo:

Sklep: enostranske meje so neskončne, kar pomeni, da je premica navpična asimptota grafa funkcije pri.
Prva meja je končna, kar pomeni, da moramo »nadaljevati pogovor« in najti drugo mejo:
Tudi druga meja je končna.
Tako je naša asimptota:
Sklep: premica, določena z enačbo, je vodoravna asimptota grafa funkcije pri.
Za iskanje horizontalne asimptote lahko uporabite poenostavljeno formulo:
Če obstaja končna meja, je ravna črta vodoravna asimptota grafa funkcije pri.
Zlahka opazimo, da sta števec in imenovalec funkcije istega reda rasti, kar pomeni, da bo iskana meja končna:

Glede na pogoj ni treba izdelati risbe, če pa smo sredi raziskovanja funkcije, potem takoj naredimo skico na osnutku:

Na podlagi treh najdenih mej poskusite sami ugotoviti, kako bi se lahko nahajal graf funkcije. Je sploh težko? Poiščite 5-6-7-8 točk in jih označite na risbi. Vendar pa je graf te funkcije zgrajen s transformacijami grafov elementarna funkcija, in bralci, ki so skrbno preučili 21. primer zgornjega članka, zlahka ugibajo, za kakšno krivuljo gre.
To je primer, ki ga morate rešiti sami. Naj vas spomnim, da je proces priročno razdeljen na dve točki - navpične asimptote in poševne asimptote. V vzorčni rešitvi se vodoravna asimptota najde po poenostavljeni shemi.
V praksi se najpogosteje srečujemo z delno-racionalnimi funkcijami in po treningu na hiperbolah bomo nalogo zapletli:
Poiščite asimptote grafa funkcije
Rešitev: ena, dve in končano:
1) Navpične asimptote so na točkah neskončne diskontinuitete, zato morate preveriti, ali gre imenovalec na nič. Odločimo se kvadratna enačba:
Diskriminanta je pozitivna, zato ima enačba dva realna korena, delo pa se znatno prišteje

Za nadaljnje iskanje enostranskih mej je priročno faktorizirati kvadratni trinom:
(za kompakten zapis je bil "minus" vključen v prvi oklepaj). Za varnost ga preverimo tako, da miselno ali na osnutku odpremo oklepaje.
Prepišimo funkcijo v obliki
Poiščimo enostranske omejitve na točki:

limita funkcije grafa asimptote
In pri bistvu:

Tako so ravne črte navpične asimptote grafa zadevne funkcije.
2) Če pogledate funkcijo, je povsem očitno, da bo limita končna in da imamo vodoravno asimptoto. Pokažimo njegovo prisotnost na kratek način:
Tako je premica (abscisna os) vodoravna asimptota grafa te funkcije.
Najdene limite in asimptote nudijo veliko informacij o grafu funkcije. Poskusite si mentalno predstavljati risbo ob upoštevanju naslednjih dejstev:

Na osnutek skicirajte svojo različico grafa.
Seveda najdene meje ne določajo jasno videza grafa in lahko naredite napako, vendar bo sama vaja zagotovila neprecenljivo pomoč pri popolni študiji funkcije. Pravilna slika je na koncu lekcije.
Poiščite asimptote grafa funkcije
Poiščite asimptote grafa funkcije
To so naloge za samostojno reševanje. Oba grafa imata ponovno vodoravne asimptote, ki jih takoj zaznamo po naslednjih značilnostih: v primeru 4 je vrstni red rasti imenovalca večji od vrstnega reda rasti števca, v primeru 5 pa sta števec in imenovalec isti vrstni red rasti. V vzorčni raztopini se prva funkcija preuči glede prisotnosti poševnih asimptot v celoti, druga pa skozi mejo.
Horizontalne asimptote so po mojem subjektivnem vtisu opazno pogostejše od tistih, ki so »resnično nagnjene«. Dolgo pričakovan splošni primer:
Poiščite asimptote grafa funkcije
Rešitev: klasika žanra:
- 1) Ker je imenovalec pozitiven, je funkcija zvezna vzdolž celotne številske premice in ni navpičnih asimptot. ...Je to dobro? Ni prava beseda - odlično! Točka št. 1 je zaprta.
- 2) Preverimo prisotnost poševnih asimptot:

Druga meja je prav tako končna, zato ima graf zadevne funkcije poševno asimptoto:
Torej, ko se graf funkcije približa ravni črti neskončno blizu.
Upoštevajte, da seka svojo poševno asimptoto v izvoru in takšne presečišča so povsem sprejemljiva - pomembno je, da je v neskončnosti "vse normalno" (pravzaprav tukaj govorimo o asimptotah).

Poiščite asimptote grafa funkcije
Rešitev: ni kaj posebnega za komentirati, zato bom narisal približen primer končne rešitve:
1) Navpične asimptote. Raziščimo bistvo.

Ravna črta je navpična asimptota za graf pri.
2) Poševne asimptote:

Ravna črta je poševna asimptota za graf pri.
Najdene enostranske meje in asimptote nam omogočajo, da z veliko zanesljivostjo napovemo, kako izgleda graf te funkcije.
Poiščite asimptote grafa funkcije
To je primer neodvisne rešitve; zaradi lažjega izračuna nekaterih omejitev lahko števec delite z imenovalcem na člen. Še enkrat, ko analizirate svoje rezultate, poskusite narisati graf te funkcije.
Očitno so lastniki "pravih" poševnih asimptot grafi tistih ulomkov racionalnih funkcij, pri katerih je najvišja stopnja števca za eno večja od najvišje stopnje imenovalca. Če je več, ne bo več poševne asimptote (na primer).
Toda v življenju se zgodijo tudi drugi čudeži.
 Geološka kronologija Paleontološka metoda temelji na preučevanju fosilnih organizmov in rastlin, zakopanih v plasti kamnin.
Geološka kronologija Paleontološka metoda temelji na preučevanju fosilnih organizmov in rastlin, zakopanih v plasti kamnin. Miti o ustvarjalnosti, ki so se izkazali za neresnične, a nam še vedno zastrupljajo življenja
Miti o ustvarjalnosti, ki so se izkazali za neresnične, a nam še vedno zastrupljajo življenja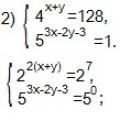 Reševanje eksponentnih enačb in neenačb
Reševanje eksponentnih enačb in neenačb