Co to jest równanie liniowe. Przykłady układów równań liniowych: metoda rozwiązań
Układ równań liniowych jest sumą n równań liniowych, z których każde zawiera k zmiennych. Jest napisane tak:
Wielu, spotykając się po raz pierwszy z wyższą algebrą, błędnie uważa, że liczba równań musi koniecznie pokrywać się z liczbą zmiennych. W algebrze szkolnej zwykle tak się dzieje, ale w algebrze wyższej na ogół nie jest to prawdą.
Rozwiązaniem układu równań jest ciąg liczb (k 1, k 2, ..., k n), który jest rozwiązaniem każdego równania układu, czyli: podstawiając do tego równania zamiast zmiennych x 1, x 2, ..., x n daje poprawną równość liczbową.
Zatem rozwiązanie układu równań oznacza znalezienie zbioru wszystkich jego rozwiązań lub udowodnienie, że zbiór ten jest pusty. Ponieważ liczba równań i liczba niewiadomych mogą się różnić, możliwe są trzy przypadki:
- System jest niespójny, tj. zbiór wszystkich rozwiązań jest pusty. Dość rzadki przypadek, który można łatwo wykryć niezależnie od metody zastosowanej do rozwiązania systemu.
- System jest spójny i zdeterminowany, tj. ma dokładnie jedno rozwiązanie. Wersja klasyczna, znana od czasów szkolnych.
- System jest spójny i nieokreślony, tj. ma nieskończenie wiele rozwiązań. To najtrudniejsza opcja. Nie wystarczy wskazać, że „system ma nieskończony zbiór rozwiązań” – trzeba opisać, jak ten zbiór jest zbudowany.
Zmienną x i nazywamy dozwoloną, jeśli występuje tylko w jednym równaniu układu i ma współczynnik równy 1. Innymi słowy, w innych równaniach współczynnik zmiennej x i musi być równy zero.
Jeśli w każdym równaniu wybierzemy jedną dozwoloną zmienną, otrzymamy zbiór dozwolonych zmiennych dla całego układu równań. Sam system napisany w tej formie będzie również nazywany rozwiązanym. Ogólnie rzecz biorąc, jeden i ten sam oryginalny system można sprowadzić do różnych dozwolonych, ale na razie się tym nie przejmujemy. Oto przykłady dozwolonych systemów:

Obydwa systemy są rozwiązywane w odniesieniu do zmiennych x 1 , x 3 i x 4 . Jednakże z takim samym sukcesem można argumentować, że drugi system jest rozwiązany w odniesieniu do x 1, x 3 i x 5. Wystarczy przepisać ostatnie równanie do postaci x 5 = x 4.
Rozważmy teraz bardziej ogólny przypadek. Miejmy w sumie k zmiennych, z których r jest dozwolone. Możliwe są wtedy dwa przypadki:
- Liczba dozwolonych zmiennych r jest równa całkowitej liczbie zmiennych k: r = k. Otrzymujemy układ k równań, w którym r = k dopuszczalnych zmiennych. Taki system jest wspólny i określony, ponieważ x 1 = b 1, x 2 = b 2, ..., x k = b k;
- Liczba dozwolonych zmiennych r jest mniejsza całkowita liczba zmienne k : r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Zatem w powyższych systemach zmienne x 2, x 5, x 6 (dla pierwszego systemu) i x 2, x 5 (dla drugiego) są dowolne. Przypadek, w którym istnieją zmienne wolne, lepiej jest sformułować jako twierdzenie:
Uwaga: to bardzo ważny punkt! W zależności od tego, jak napiszesz wynikowy system, ta sama zmienna może być dozwolona lub bezpłatna. Większość nauczycieli matematyki na poziomie wyższym zaleca zapisywanie zmiennych w porządku leksykograficznym, tj. indeks rosnący. Nie masz jednak obowiązku stosowania się do tej porady.
Twierdzenie. Jeżeli w układzie n równań dopuszczalne są zmienne x 1, x 2, ..., x r oraz x r + 1, x r + 2, ..., x k są wolne, to:
- Jeśli ustalimy wartości zmiennych wolnych (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k), a następnie znajdziemy wartości x 1, x 2, ..., x r, otrzymujemy jedną z decyzji.
- Jeśli w dwóch rozwiązaniach wartości zmiennych wolnych są zbieżne, to wartości zmiennych dozwolonych również są zbieżne, tj. rozwiązania są równe.
Jakie jest znaczenie tego twierdzenia? Aby otrzymać wszystkie rozwiązania rozwiązanego układu równań, wystarczy wyizolować zmienne swobodne. Następnie przypisując różne wartości wolnym zmiennym otrzymujemy gotowe rozwiązania. To wszystko - w ten sposób można uzyskać wszystkie rozwiązania systemu. Nie ma innych rozwiązań.
Wniosek: rozwiązany układ równań jest zawsze spójny. Jeśli liczba równań w rozwiązanym układzie jest równa liczbie zmiennych, układ będzie określony; jeśli jest mniejszy, będzie nieokreślony.
I wszystko byłoby dobrze, ale pojawia się pytanie: jak uzyskać rozwiązany z pierwotnego układu równań? Do tego istnieje
Itd. Logiczne jest zapoznanie się z równaniami innych typów. Następne w kolejce są równania liniowe, którego ukierunkowana nauka rozpoczyna się na lekcjach algebry w 7. klasie.
Oczywiste jest, że najpierw musisz wyjaśnić, czym jest równanie liniowe, podać definicję równania liniowego, jego współczynniki, pokazać je widok ogólny. Następnie możesz dowiedzieć się, ile rozwiązań ma równanie liniowe w zależności od wartości współczynników i sposobu znalezienia pierwiastków. Umożliwi to przejście do rozwiązywania przykładów, a tym samym utrwalenia poznanej teorii. W tym artykule zrobimy to: szczegółowo omówimy wszystkie teoretyczne i praktyczne punkty dotyczące równań liniowych i ich rozwiązań.
Powiedzmy od razu, że tutaj rozważymy tylko równania liniowe z jedną zmienną, a w osobnym artykule przestudiujemy zasady rozwiązywania równania liniowe z dwiema zmiennymi.
Nawigacja strony.
Co to jest równanie liniowe?
Definicja równania liniowego wynika ze sposobu jego zapisu. Ponadto w różnych podręcznikach matematyki i algebry sformułowania definicji równań liniowych wykazują pewne różnice, które nie wpływają na istotę zagadnienia.
Na przykład w podręczniku algebry dla klasy 7 autorstwa Yu N. Makarycheva i in. równanie liniowe zdefiniowano w następujący sposób:
Definicja.
Równanie postaci ax=b, gdzie x jest zmienną, a i b są liczbami, nazywa się równanie liniowe z jedną zmienną.
Podajmy przykłady równań liniowych spełniających podaną definicję. Na przykład 5 x = 10 jest równaniem liniowym z jedną zmienną x, tutaj współczynnik a wynosi 5, a liczba b wynosi 10. Inny przykład: −2,3·y=0 to także równanie liniowe, ale ze zmienną y, w której a=−2,3 i b=0. Natomiast w równaniach liniowych x=−2 i −x=3,33 a nie występują jawnie i wynoszą odpowiednio 1 i −1, natomiast w pierwszym równaniu b=−2, a w drugim – b=3,33.
A rok wcześniej w podręczniku matematyki N. Ya Vilenkina równania liniowe z jedną niewiadomą, oprócz równań w postaci a x = b, rozważały także równania, które można doprowadzić do tej postaci, przenosząc wyrazy z jednej części. równania na inne o przeciwnym znaku, a także poprzez redukcję wyrazów podobnych. Zgodnie z tą definicją równania w postaci 5 x = 2 x + 6 itd. również liniowy.
Z kolei w podręczniku algebry dla klasy 7 autorstwa A. G. Mordkovicha podana jest następująca definicja:
Definicja.
Równanie liniowe z jedną zmienną x jest równaniem w postaci a·x+b=0, gdzie aib to liczby zwane współczynnikami równania liniowego.
Na przykład równania liniowe tego typu to 2 x−12=0, tutaj współczynnik a wynosi 2, a b wynosi –12, a 0,2 y+4,6=0 ze współczynnikami a=0,2 i b =4,6. Ale jednocześnie istnieją przykłady równań liniowych, które mają postać nie a·x+b=0, ale a·x=b, na przykład 3·x=12.
Aby w przyszłości nie było żadnych rozbieżności, przez równanie liniowe z jedną zmienną x i współczynnikami a i b rozumiemy równanie w postaci a x + b = 0. Ten typ równań liniowych wydaje się najbardziej uzasadniony, gdyż równania liniowe takie są równania algebraiczne pierwszy stopień. I wszystkie inne równania wskazane powyżej, a także równania, które za pomocą równoważnych przekształceń sprowadzają się do postaci a x + b = 0, nazwiemy równania sprowadzające się do równań liniowych. Przy takim podejściu równanie 2 x+6=0 jest równaniem liniowym, a 2 x=−6, 4+25 y=6+24 y, 4 (x+5)=12 itd. - To są równania, które sprowadzają się do równań liniowych.
Jak rozwiązywać równania liniowe?
Teraz czas dowiedzieć się, jak rozwiązuje się równania liniowe a·x+b=0. Innymi słowy, czas dowiedzieć się, czy równanie liniowe ma pierwiastki, a jeśli tak, to ile ich jest i jak je znaleźć.
Obecność pierwiastków równania liniowego zależy od wartości współczynników aib. W tym przypadku równanie liniowe a x+b=0 ma
- jedyny pierwiastek dla a≠0,
- nie ma pierwiastków dla a=0 i b≠0,
- ma nieskończenie wiele pierwiastków dla a=0 i b=0, w którym to przypadku dowolna liczba jest pierwiastkiem równania liniowego.
Wyjaśnijmy, w jaki sposób uzyskano te wyniki.
Wiemy, że do rozwiązywania równań możemy przejść od równania pierwotnego do równań równoważnych, czyli do równań z tymi samymi pierwiastkami lub, jak pierwotne, bez pierwiastków. Aby to zrobić, możesz użyć następujących równoważnych przekształceń:
- przeniesienie wyrazu z jednej części równania do drugiej o przeciwnym znaku,
- a także mnożenie lub dzielenie obu stron równania przez tę samą liczbę niezerową.
Zatem w równaniu liniowym z jedną zmienną w postaci a·x+b=0 możemy przenieść wyraz b z lewej strony na prawą z przeciwnym znakiem. W tym przypadku równanie przyjmie postać a·x=−b.
A potem nasuwa się pytanie, jak podzielić obie strony równania przez liczbę a. Ale jest jedno: liczba a może być równa zeru i wtedy taki podział jest niemożliwy. Aby uporać się z tym problemem, założymy najpierw, że liczba a jest różna od zera, a przypadek bycia równym zero rozważymy osobno nieco później.
Zatem, gdy a nie jest równe zero, wówczas możemy podzielić obie strony równania a·x=−b przez a, po czym zostanie ono przekształcone do postaci x=(−b):a, wynik ten można zapisać zapisywane przy użyciu ukośnika ułamkowego jako.
Zatem dla a≠0 równanie liniowe a·x+b=0 jest równoważne równaniu, z którego widoczny jest jego pierwiastek.
Łatwo pokazać, że pierwiastek ten jest jednoznaczny, czyli równanie liniowe nie ma innych pierwiastków. Dzięki temu możesz zastosować odwrotną metodę.
Oznaczmy pierwiastek jako x 1. Załóżmy, że istnieje jeszcze jeden pierwiastek równania liniowego, który oznaczamy jako x 2 oraz x 2 ≠x 1, który ze względu na wyznaczanie równych liczb poprzez różnicę jest równoważne warunkowi x 1 − x 2 ≠0. Ponieważ x 1 i x 2 są pierwiastkami równania liniowego a·x+b=0, to równości liczbowe a·x 1 +b=0 i a·x 2 +b=0 są spełnione. Możemy odjąć odpowiednie części tych równości, na co pozwalają nam właściwości równości numerycznych, mamy a·x 1 +b−(a·x 2 +b)=0−0, z czego a·(x 1 −x 2)+( b−b)=0 i wtedy a·(x 1 −x 2)=0 . Ale ta równość jest niemożliwa, ponieważ zarówno a≠0, jak i x 1 − x 2 ≠0. Doszliśmy więc do sprzeczności, która dowodzi jednoznaczności pierwiastka równania liniowego a·x+b=0 dla a≠0.
W ten sposób rozwiązaliśmy równanie liniowe a·x+b=0 dla a≠0. Pierwszy wynik podany na początku tego akapitu jest uzasadniony. Pozostały jeszcze dwa spełniające warunek a=0.
Gdy a=0, równanie liniowe a·x+b=0 przyjmuje postać 0·x+b=0. Z tego równania i własności mnożenia liczb przez zero wynika, że niezależnie od tego, jaką liczbę przyjmiemy jako x, jeśli podstawimy ją do równania 0 x + b=0, otrzymamy równość liczbową b=0. Równość ta jest prawdziwa, gdy b=0, a w pozostałych przypadkach, gdy b≠0, równość ta jest fałszywa.
W konsekwencji, przy a=0 i b=0, pierwiastkiem równania liniowego a·x+b=0 jest dowolna liczba, ponieważ w tych warunkach podstawienie dowolnej liczby za x daje poprawną równość liczbową 0=0. A gdy a=0 i b≠0, równanie liniowe a·x+b=0 nie ma pierwiastków, gdyż w tych warunkach podstawienie dowolnej liczby za x prowadzi do błędnej równości liczbowej b=0.
Podane uzasadnienia pozwalają na sformułowanie ciągu działań pozwalającego na rozwiązanie dowolnego równania liniowego. Więc, algorytm rozwiązywania równań liniowych Jest:
- Najpierw, pisząc równanie liniowe, znajdujemy wartości współczynników a i b.
- Jeśli a=0 i b=0, to równanie to ma nieskończenie wiele pierwiastków, czyli pierwiastkiem tego równania liniowego jest dowolna liczba.
- Jeśli a jest niezerowe, to
- współczynnik b przenosimy na prawą stronę z przeciwnym znakiem i równanie liniowe przekształcamy do postaci a·x=−b,
- po czym obie strony powstałego równania dzieli się przez niezerową liczbę a, co daje pożądany pierwiastek pierwotnego równania liniowego.
Napisany algorytm stanowi kompleksową odpowiedź na pytanie, jak rozwiązywać równania liniowe.
Podsumowując ten punkt, warto stwierdzić, że podobny algorytm stosuje się do rozwiązywania równań w postaci a·x=b. Różnica polega na tym, że gdy a≠0, obie strony równania są natychmiast dzielone przez tę liczbę; tutaj b jest już w wymaganej części równania i nie ma potrzeby jego przenoszenia.
Aby rozwiązać równania w postaci a x = b, stosuje się następujący algorytm:
- Jeśli a=0 i b=0, to równanie ma nieskończenie wiele pierwiastków, które są dowolnymi liczbami.
- Jeśli a=0 i b≠0, to pierwotne równanie nie ma pierwiastków.
- Jeżeli a jest niezerowe, to obie strony równania dzieli się przez niezerową liczbę a, z której znajduje się jedyny pierwiastek równania równy b/a.
Przykłady rozwiązywania równań liniowych
Przejdźmy do ćwiczeń. Przyjrzyjmy się, jak wykorzystywany jest algorytm rozwiązywania równań liniowych. Przedstawmy rozwiązania typowych przykładów odpowiadających różnym wartościom współczynników równań liniowych.
Przykład.
Rozwiąż równanie liniowe 0·x−0=0.
Rozwiązanie.
W tym równaniu liniowym a=0 i b=−0, co jest tym samym, co b=0. Dlatego to równanie ma nieskończenie wiele pierwiastków; pierwiastkiem jest dowolna liczba.
Odpowiedź:
x – dowolna liczba.
Przykład.
Czy równanie liniowe 0 x + 2,7 = 0 ma rozwiązania?
Rozwiązanie.
W tym przypadku współczynnik a jest równy zero, a współczynnik b tego równania liniowego jest równy 2,7, czyli różny od zera. Dlatego równanie liniowe nie ma pierwiastków.
Równania. Inaczej mówiąc, rozwiązanie wszystkich równań zaczyna się od tych przekształceń. Przy rozwiązywaniu równań liniowych opiera się ono (rozwiązanie) na przekształceniach tożsamości i kończy się ostateczną odpowiedzią.
Przypadek niezerowego współczynnika dla nieznanej zmiennej.
topór+b=0, a ≠ 0
Wyrazy z X przesuwamy na jedną stronę, a liczby na drugą. Pamiętaj, że przenosząc wyrazy na przeciwną stronę równania, musisz zmienić znak:
topór:(a)=-b:(a)
Skróćmy A Na X i otrzymujemy:
x=-b:(a)
To jest odpowiedź. Jeśli chcesz sprawdzić, czy liczba jest -b:(a) pierwiastek naszego równania, to zamiast tego musimy zastąpić równanie początkowe X to jest numer:
a(-b:(a))+b=0 ( te. 0=0)
Ponieważ ta równość jest zatem poprawna -b:(a) a prawda jest pierwiastkiem równania.
Odpowiedź: x=-b:(a), a ≠ 0.
Pierwszy przykład:
5x+2=7x-6
Przesuwamy terminy z na jedną stronę X, a po drugiej stronie cyfry:
5x-7x=-6-2
-2x:(-2)=-8:(-2)
Jeśli nie było wiadomo, współczynnik został zmniejszony i otrzymaliśmy odpowiedź:
To jest odpowiedź. Jeśli chcesz sprawdzić, czy liczba 4 jest rzeczywiście pierwiastkiem naszego równania, podstawiamy tę liczbę zamiast X w pierwotnym równaniu:
5*4+2=7*4-6 ( te. 22=22)
Ponieważ ta równość jest prawdziwa, wówczas 4 jest pierwiastkiem równania.
Drugi przykład:
Rozwiąż równanie:
5x+14=x-49
Przesuwając niewiadome i liczby w różnych kierunkach, otrzymaliśmy:
Podziel części równania przez współczynnik przy X(o 4) i otrzymujemy:
![]()
Trzeci przykład:
Rozwiąż równanie:
![]()
Najpierw pozbywamy się irracjonalności współczynnika nieznanego, mnożąc wszystkie wyrazy przez:
![]()
![]()
Formularz ten uważa się za uproszczony, ponieważ liczba ma pierwiastek z liczby w mianowniku. Musimy uprościć odpowiedź, mnożąc licznik i mianownik przez tę samą liczbę, mamy to:
![]()
Sprawa bez rozwiązań.
Rozwiąż równanie:
2x+3=2x+7
Na oczach wszystkich X nasze równanie nie stanie się prawdziwą równością. Oznacza to, że nasze równanie nie ma pierwiastków.
Odpowiedź: nie ma rozwiązań.
Szczególnym przypadkiem jest nieskończona liczba rozwiązań.
Rozwiąż równanie:
2x+3=2x+3
Przesuwając x i liczby w różnych kierunkach i dodając podobne wyrazy, otrzymujemy równanie:
Tutaj również nie można podzielić obu części przez 0, ponieważ jest to zabronione. Jednak umieszczenie X dowolną liczbę, otrzymamy poprawną równość. Oznacza to, że każda liczba jest rozwiązaniem takiego równania. Zatem istnieje nieskończona liczba rozwiązań.
Odpowiedź: nieskończona liczba rozwiązań.
Przypadek równości dwóch form pełnych.
topór+b=cx+d
ax-cx=d-b
(a-c)x=d-b
x=(d-b):(a-c)
Odpowiedź: x=(d-b):(a-c), Jeśli d≠b i a≠c, w przeciwnym razie istnieje nieskończenie wiele rozwiązań, ale jeśli a=c, A d≠b, to nie ma rozwiązań.
W tym filmie przeanalizujemy cały zestaw równań liniowych rozwiązywanych przy użyciu tego samego algorytmu - dlatego nazywane są one najprostszymi.
Najpierw zdefiniujmy: co to jest równanie liniowe i które nazywa się najprostszym?
Równanie liniowe to takie, w którym występuje tylko jedna zmienna i tylko do pierwszego stopnia.
Najprostsze równanie oznacza konstrukcję:
Wszystkie pozostałe równania liniowe sprowadzamy do najprostszych za pomocą algorytmu:
- Rozwiń nawiasy, jeśli istnieją;
- Przenieś terminy zawierające zmienną na jedną stronę znaku równości, a terminy bez zmiennej na drugą;
- Podaj podobne wyrazy po lewej i prawej stronie znaku równości;
- Podziel powstałe równanie przez współczynnik zmiennej $x$.
Oczywiście ten algorytm nie zawsze pomaga. Faktem jest, że czasem po tych wszystkich zabiegach współczynnik zmiennej $x$ okazuje się równy zeru. W takim przypadku możliwe są dwie opcje:
- Równanie nie ma w ogóle rozwiązań. Na przykład, gdy okaże się, że $0\cdot x=8$, tj. po lewej stronie jest zero, a po prawej liczba różna od zera. W poniższym filmie przyjrzymy się kilku powodom, dla których taka sytuacja jest możliwa.
- Rozwiązaniem są wszystkie liczby. Jest to możliwe tylko wtedy, gdy równanie zostało sprowadzone do konstrukcji $0\cdot x=0$. Jest całkiem logiczne, że niezależnie od tego, jakie $x$ podstawimy, i tak okaże się, że „zero jest równe zeru”, tj. poprawna równość liczbowa.
Zobaczmy teraz, jak to wszystko działa na przykładach z życia wziętych.
Przykłady rozwiązywania równań
Dziś mamy do czynienia z równaniami liniowymi i to tylko najprostszymi. Ogólnie równanie liniowe oznacza dowolną równość, która zawiera dokładnie jedną zmienną i dotyczy tylko pierwszego stopnia.
Takie konstrukcje rozwiązuje się w przybliżeniu w ten sam sposób:
- Przede wszystkim należy rozwinąć nawiasy, jeśli takie istnieją (jak w naszym ostatnim przykładzie);
- Następnie połącz podobnie
- Na koniec wyizoluj zmienną, tj. przesuń wszystko, co jest związane ze zmienną – terminy, w jakich jest ona zawarta – na jedną stronę, a wszystko, co pozostaje bez niej, na drugą stronę.
Następnie z reguły trzeba przynieść podobne po każdej stronie powstałej równości, a potem pozostaje tylko podzielić przez współczynnik „x” i otrzymamy ostateczną odpowiedź.
W teorii wygląda to ładnie i prosto, ale w praktyce nawet doświadczeni uczniowie szkół średnich mogą popełniać obraźliwe błędy w dość prostych równaniach liniowych. Zazwyczaj błędy popełniane są podczas otwierania nawiasów lub przy obliczaniu „plusów” i „minusów”.
Ponadto zdarza się, że równanie liniowe w ogóle nie ma rozwiązań lub że rozwiązaniem jest cała oś liczbowa, tj. dowolny numer. Przyjrzymy się tym subtelnościom podczas dzisiejszej lekcji. Ale zaczniemy, jak już zrozumiałeś, od najprostszych zadań.
Schemat rozwiązywania prostych równań liniowych
Najpierw napiszę jeszcze raz cały schemat rozwiązywania najprostszych równań liniowych:
- Rozwiń nawiasy, jeśli występują.
- Izolujemy zmienne, tj. Przenosimy wszystko, co zawiera „X” na jedną stronę, a wszystko bez „X” na drugą.
- Przedstawiamy podobne terminy.
- Wszystko dzielimy przez współczynnik „x”.
Oczywiście ten schemat nie zawsze działa; są w nim pewne subtelności i sztuczki, a teraz je poznamy.
Rozwiązywanie rzeczywistych przykładów prostych równań liniowych
Zadanie nr 1
Pierwszy krok wymaga od nas otwarcia nawiasów. Ale nie ma ich w tym przykładzie, więc je pominiemy ten etap. W drugim kroku musimy wyizolować zmienne. Uwaga: mówimy tylko o warunkach indywidualnych. Zapiszmy to:
Podobne terminy prezentujemy po lewej i prawej stronie, ale tutaj zostało to już zrobione. Dlatego przechodzimy do czwartego kroku: podziel przez współczynnik:
\[\frac(6x)(6)=-\frac(72)(6)\]
Więc otrzymaliśmy odpowiedź.
Zadanie nr 2
W tym zadaniu widzimy nawiasy, więc rozwińmy je:
Zarówno po lewej, jak i po prawej stronie widzimy mniej więcej ten sam projekt, ale postępujmy zgodnie z algorytmem, tj. oddzielanie zmiennych:
Oto kilka podobnych:
U jakich korzeni to działa? Odpowiedź: dla każdego. Zatem możemy napisać, że $x$ jest dowolną liczbą.
Zadanie nr 3
Trzecie równanie liniowe jest bardziej interesujące:
\[\lewo(6-x \prawo)+\lewo(12+x \prawo)-\lewo(3-2x \prawo)=15\]
Nawiasów jest kilka, ale nie są one przez nic mnożone, są po prostu poprzedzane różne znaki. Podzielmy je:
Wykonujemy drugi znany nam już krok:
\[-x+x+2x=15-6-12+3\]
Zróbmy matematykę:
Wykonujemy ostatni krok - dzielimy wszystko przez współczynnik „x”:
\[\frac(2x)(x)=\frac(0)(2)\]
O czym należy pamiętać przy rozwiązywaniu równań liniowych
Jeśli pominiemy zbyt proste zadania, chciałbym powiedzieć, co następuje:
- Jak powiedziałem powyżej, nie każde równanie liniowe ma rozwiązanie - czasami po prostu nie ma pierwiastków;
- Nawet jeśli są korzenie, może być wśród nich zero - nie ma w tym nic złego.
Zero to taka sama liczba jak pozostałe; nie powinieneś go w żaden sposób dyskryminować ani zakładać, że jeśli otrzymasz zero, oznacza to, że zrobiłeś coś złego.
Kolejna funkcja związana jest z otwieraniem nawiasów. Uwaga: jeśli przed nimi znajduje się „minus”, usuwamy go, ale w nawiasach zmieniamy znaki na naprzeciwko. A potem możemy go otworzyć za pomocą standardowych algorytmów: otrzymamy to, co widzieliśmy w powyższych obliczeniach.
Zrozumienie tego prostego faktu pomoże ci uniknąć popełniania głupich i bolesnych błędów w szkole średniej, gdy robienie takich rzeczy jest oczywiste.
Rozwiązywanie złożonych równań liniowych
Przejdźmy do bardziej złożonych równań. Teraz konstrukcje staną się bardziej złożone i przy wykonywaniu różnych przekształceń pojawi się funkcja kwadratowa. Nie powinniśmy się jednak tego bać, gdyż jeśli zgodnie z planem autora rozwiązujemy równanie liniowe, to w procesie transformacji wszystkie jednomiany zawierające funkcję kwadratową koniecznie się zniosą.
Przykład nr 1
Oczywiście pierwszym krokiem jest otwarcie nawiasów. Zróbmy to bardzo ostrożnie:
Przyjrzyjmy się teraz prywatności:
\[-x+6((x)^(2))-6((x)^(2))+x=-12\]
Oto kilka podobnych:
Oczywiście to równanie nie ma rozwiązań, więc napiszemy to w odpowiedzi:
\[\varnic\]
albo nie ma korzeni.
Przykład nr 2
Wykonujemy te same czynności. Pierwszy krok:
Przesuńmy wszystko ze zmienną w lewo, a bez niej - w prawo:
Oto kilka podobnych:
Oczywiście to równanie liniowe nie ma rozwiązania, więc zapiszemy je w ten sposób:
\[\varnic\],
albo nie ma korzeni.
Niuanse rozwiązania
Obydwa równania są całkowicie rozwiązane. Na przykładzie tych dwóch wyrażeń po raz kolejny przekonaliśmy się, że nawet w najprostszych równaniach liniowych wszystko może nie być takie proste: pierwiastków może być albo jeden, albo żaden, albo nieskończenie wiele pierwiastków. W naszym przypadku rozważaliśmy dwa równania, oba po prostu nie mają pierwiastków.
Chciałbym jednak zwrócić uwagę na inny fakt: jak pracować z nawiasami i jak je otwierać, jeśli przed nimi znajduje się znak minus. Rozważ to wyrażenie:
Przed otwarciem musisz pomnożyć wszystko przez „X”. Uwaga: mnoży się każdy indywidualny termin. Wewnątrz znajdują się dwa terminy - odpowiednio dwa terminy i pomnożone.
I dopiero po dokonaniu tych pozornie elementarnych, ale bardzo ważnych i niebezpiecznych przekształceń, można otworzyć nawias z punktu widzenia tego, że po nim znajduje się znak minus. Tak, tak: dopiero teraz, gdy przekształcenia zostaną zakończone, pamiętamy, że przed nawiasem jest znak minus, co oznacza, że wszystko poniżej po prostu zmienia znaki. Jednocześnie znikają same nawiasy i, co najważniejsze, znika również przedni „minus”.
To samo robimy z drugim równaniem:
To nie przypadek, że zwracam uwagę na te drobne, pozornie nieistotne fakty. Bo rozwiązywanie równań to zawsze ciąg elementarnych przekształceń, gdzie nieumiejętność jasnego i kompetentnego wykonania prostych czynności powoduje, że licealiści przychodzą do mnie i na nowo uczą się rozwiązywać takie proste równania.
Oczywiście nadejdzie dzień, kiedy udoskonalisz te umiejętności do punktu automatyzmu. Nie będziesz już musiał za każdym razem wykonywać tylu przekształceń; zapiszesz wszystko w jednej linii. Ale kiedy dopiero się uczysz, musisz napisać każdą akcję osobno.
Rozwiązywanie jeszcze bardziej złożonych równań liniowych
To, co teraz rozwiążemy, trudno nazwać najprostszym zadaniem, ale znaczenie pozostaje takie samo.
Zadanie nr 1
\[\lewo(7x+1 \prawo)\lewo(3x-1 \prawo)-21((x)^(2))=3\]
Pomnóżmy wszystkie elementy w pierwszej części:
Zadbajmy o prywatność:
Oto kilka podobnych:
Dokończmy ostatni krok:
\[\frac(-4x)(4)=\frac(4)(-4)\]
Oto nasza ostateczna odpowiedź. I mimo że w rozwiązywaniu mieliśmy współczynniki z funkcją kwadratową, to znosiły się one nawzajem, przez co równanie było liniowe, a nie kwadratowe.
Zadanie nr 2
\[\lewo(1-4x \prawo)\lewo(1-3x \prawo)=6x\lewo(2x-1 \prawo)\]
Wykonajmy ostrożnie pierwszy krok: pomnóż każdy element z pierwszego nawiasu przez każdy element z drugiego. Po przekształceniach powinny powstać w sumie cztery nowe terminy:
Teraz ostrożnie wykonajmy mnożenie w każdym wyrazie:
Przesuńmy terminy z „X” w lewo, a te bez – w prawo:
\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]
Oto podobne terminy:
Po raz kolejny otrzymaliśmy ostateczną odpowiedź.
Niuanse rozwiązania
Najważniejsza uwaga dotycząca tych dwóch równań jest następująca: gdy tylko zaczniemy mnożyć nawiasy zawierające więcej niż jeden wyraz, robimy to według następującej zasady: pierwszy wyraz bierzemy z pierwszego i mnożymy przez każdy element z drugi; następnie bierzemy drugi element z pierwszego i podobnie mnożymy przez każdy element drugiego. W rezultacie będziemy mieli cztery kadencje.
O sumie algebraicznej
W tym ostatnim przykładzie chciałbym przypomnieć uczniom, czym jest suma algebraiczna. W matematyce klasycznej przez 1-7 dolarów rozumiemy prostą konstrukcję: odejmij siedem od jednego. W algebrze rozumiemy przez to: do liczby „jeden” dodajemy kolejną liczbę, a mianowicie „minus siedem”. Tym właśnie różni się suma algebraiczna od zwykłej sumy arytmetycznej.
Gdy tylko podczas wykonywania wszystkich przekształceń, każdego dodawania i mnożenia zaczniesz widzieć konstrukcje podobne do opisanych powyżej, po prostu nie będziesz mieć żadnych problemów z algebrą podczas pracy z wielomianami i równaniami.
Na koniec spójrzmy na jeszcze kilka przykładów, które będą jeszcze bardziej złożone niż te, które właśnie sprawdziliśmy, i aby je rozwiązać, będziemy musieli nieco rozszerzyć nasz standardowy algorytm.
Rozwiązywanie równań z ułamkami
Aby rozwiązać takie zadania, będziemy musieli dodać do naszego algorytmu jeszcze jeden krok. Ale najpierw przypomnę Ci nasz algorytm:
- Otwórz nawiasy.
- Oddzielne zmienne.
- Przynieś podobne.
- Podziel przez stosunek.
Niestety, ten wspaniały algorytm, przy całej swojej skuteczności, okazuje się nie do końca odpowiedni, gdy mamy przed sobą ułamki. Jak zobaczymy poniżej, w obu równaniach mamy ułamek zarówno po lewej, jak i po prawej stronie.
Jak pracować w tym przypadku? Tak, to bardzo proste! Aby to zrobić, należy dodać do algorytmu jeszcze jeden krok, który można wykonać zarówno przed, jak i po pierwszej akcji, a mianowicie pozbycie się ułamków. Zatem algorytm będzie następujący:
- Pozbądź się ułamków.
- Otwórz nawiasy.
- Oddzielne zmienne.
- Przynieś podobne.
- Podziel przez stosunek.
Co to znaczy „pozbyć się ułamków”? Dlaczego można to zrobić zarówno po, jak i przed pierwszym standardowym krokiem? W rzeczywistości w naszym przypadku wszystkie ułamki są liczbowe w swoim mianowniku, tj. Wszędzie mianownik jest po prostu liczbą. Dlatego jeśli pomnożymy obie strony równania przez tę liczbę, pozbędziemy się ułamków.
Przykład nr 1
\[\frac(\lewo(2x+1 \prawo)\lewo(2x-3 \prawo))(4)=((x)^(2))-1\]
Pozbądźmy się ułamków w tym równaniu:
\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]
Uwaga: wszystko jest mnożone raz przez „cztery”, tj. to, że masz dwa nawiasy, nie oznacza, że musisz pomnożyć każdy z nich przez „cztery”. Zapiszmy:
\[\lewo(2x+1 \prawo)\lewo(2x-3 \prawo)=\lewo(((x)^(2))-1 \prawo)\cdot 4\]
Teraz rozwińmy:
Wykluczamy zmienną:
Dokonujemy redukcji wyrazów podobnych:
\[-4x=-1\lewo| :\lewo(-4 \prawo) \prawo.\]
\[\frac(-4x)(-4)=\frac(-1)(-4)\]
Otrzymaliśmy ostateczne rozwiązanie, przejdźmy do drugiego równania.
Przykład nr 2
\[\frac(\lewo(1-x \prawo)\lewo(1+5x \prawo))(5)+((x)^(2))=1\]
Tutaj wykonujemy te same czynności:
\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]
\[\frac(4x)(4)=\frac(4)(4)\]
Problem został rozwiązany.
Właściwie to wszystko, co chciałem wam dzisiaj powiedzieć.
Kluczowe punkty
Kluczowe ustalenia to:
- Znać algorytm rozwiązywania równań liniowych.
- Możliwość otwierania nawiasów.
- Nie martw się, jeśli zobaczysz funkcje kwadratowe najprawdopodobniej w procesie dalszych przekształceń ulegną zmniejszeniu.
- Istnieją trzy rodzaje pierwiastków w równaniach liniowych, nawet najprostszych: jeden pojedynczy pierwiastek, cała oś liczbowa jest pierwiastkiem i nie ma żadnych pierwiastków.
Mam nadzieję, że ta lekcja pomoże ci opanować prosty, ale bardzo ważny temat dla dalszego zrozumienia całej matematyki. Jeśli coś nie jest jasne, wejdź na stronę i rozwiąż przedstawione tam przykłady. Bądź na bieżąco, czeka Cię jeszcze wiele ciekawych rzeczy!
 Tajna wyprawa OGPU do tajemniczej krainy Szambali
Tajna wyprawa OGPU do tajemniczej krainy Szambali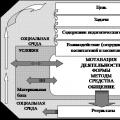 Naukowa biblioteka elektroniczna Proces pedagogiczny reprezentuje
Naukowa biblioteka elektroniczna Proces pedagogiczny reprezentuje Prezentacja na temat „A.A. Blok”. Prezentacja na temat „Aleksander Aleksandrowicz Blok” Rodzina i krewni
Prezentacja na temat „A.A. Blok”. Prezentacja na temat „Aleksander Aleksandrowicz Blok” Rodzina i krewni