Nierówności. Rodzaje nierówności
Program do rozwiązywania nierówności liniowych, kwadratowych i ułamkowych nie tylko daje odpowiedź na problem, ale dostarcza szczegółowe rozwiązanie wraz z objaśnieniami, tj. wyświetla proces rozwiązywania sprawdzający wiedzę z matematyki i/lub algebry.
Ponadto, jeśli w procesie rozwiązywania którejś z nierówności konieczne jest rozwiązanie np. równania kwadratowego, wówczas wyświetlane jest również jego szczegółowe rozwiązanie (zawarte jest w spoilerze).
Program ten może być przydatny dla uczniów szkół średnich w przygotowaniach do egzaminu testy, rodzicom, aby monitorowali sposoby rozwiązywania nierówności przez swoje dzieci.
Program ten może być przydatny dla uczniów szkół średnich szkoły średnie w przygotowaniu do sprawdzianów i egzaminów, podczas sprawdzania wiedzy przed Unified State Exam, aby rodzice mogli kontrolować rozwiązanie wielu problemów z matematyki i algebry. A może wynajęcie korepetytora lub zakup nowych podręczników jest dla Ciebie zbyt kosztowny? A może po prostu chcesz to zrobić jak najszybciej? praca domowa
na matematyce lub algebrze? W tym przypadku możesz także skorzystać z naszych programów ze szczegółowymi rozwiązaniami.
W ten sposób możesz prowadzić własne szkolenie i/lub szkolenie swoich młodszych braci, a jednocześnie wzrasta poziom edukacji w zakresie rozwiązywania problemów.
Zasady wpisywania nierówności
Dowolna litera łacińska może działać jako zmienna.
Na przykład: \(x, y, z, a, b, c, o, p, q\) itp.
Liczby można wprowadzać jako liczby całkowite lub ułamkowe.
Co więcej, liczby ułamkowe można wprowadzać nie tylko w postaci ułamka dziesiętnego, ale także w postaci ułamka zwykłego.
Zasady wprowadzania ułamków dziesiętnych.
W ułamkach dziesiętnych część ułamkową można oddzielić od całości kropką lub przecinkiem. Możesz na przykład wejść miejsca dziesiętne
w ten sposób: 2,5x - 3,5x^2
Zasady wpisywania ułamków zwykłych.
Tylko liczba całkowita może pełnić rolę licznika, mianownika i części całkowitej ułamka.
Mianownik nie może być ujemny. Przy wejściu ułamek liczbowy /
Licznik oddziela się od mianownika znakiem dzielenia: &
Cała część jest oddzielona od ułamka znakiem ampersandu:
Wejście: 3 i 1/3 - 5 i 6/5 lat +1/7 lat^2
Wynik: \(3\frac(1)(3) - 5\frac(6)(5) y + \frac(1)(7)y^2 \)
Podczas wprowadzania wyrażeń można używać nawiasów. W tym przypadku przy rozwiązywaniu nierówności najpierw upraszcza się wyrażenia. Na przykład:
Wybierz żądany znak nierówności i wprowadź wielomiany w pola poniżej.
Rozwiązać układ nierówności Odkryto, że niektóre skrypty niezbędne do rozwiązania tego problemu nie zostały załadowane i program może nie działać.
Być może masz włączonego AdBlocka.
W takim przypadku wyłącz ją i odśwież stronę.
Aby rozwiązanie się pojawiło, musisz włączyć JavaScript.
Poniżej znajdują się instrukcje dotyczące włączania JavaScript w Twojej przeglądarce.
Ponieważ Chętnych do rozwiązania problemu jest wiele, Twoja prośba została umieszczona w kolejce.
Za kilka sekund rozwiązanie pojawi się poniżej.
Proszę czekać sekunda...
Jeśli ty zauważył błąd w rozwiązaniu, możesz napisać o tym w Formularzu opinii.
Nie zapomnij wskaż, które zadanie ty decydujesz co wpisz w pola.
Nasze gry, puzzle, emulatory:
Trochę teorii.
Układy nierówności z jedną niewiadomą. Przedziały numeryczne
W siódmej klasie zapoznałeś się z koncepcją systemu i nauczyłeś się rozwiązywać systemy równania liniowe z dwiema niewiadomymi. Następnie rozważymy układy nierówności liniowych z jedną niewiadomą. Zbiory rozwiązań układów nierówności można zapisać za pomocą przedziałów (przedziałów, półprzedziałów, odcinków, półprostych). Zapoznasz się także z notacją przedziałów liczbowych.
Jeżeli w nierównościach \(4x > 2000\) i \(5x \leq 4000\) nieznana liczba x jest taka sama, to nierówności te rozpatrywane są łącznie i mówi się, że tworzą układ nierówności: $$ \left\ (\begin(tablica)(l) 4x > 2000 \\ 5x \leq 4000 \end(tablica)\right $$.
Nawias klamrowy pokazuje, że należy znaleźć wartości x, dla których obie nierówności układu zamieniają się w prawidłowe nierówności numeryczne. Układ ten jest przykładem układu nierówności liniowych z jedną niewiadomą.
Rozwiązaniem układu nierówności z jedną niewiadomą jest wartość niewiadomej, przy której wszystkie nierówności układu zamieniają się w prawdziwe nierówności liczbowe. Rozwiązanie układu nierówności oznacza znalezienie wszystkich rozwiązań tego układu lub stwierdzenie, że ich nie ma.
Nierówności \(x \geq -2 \) i \(x \leq 3 \) można zapisać jako nierówność podwójną: \(-2 \leq x \leq 3 \).
Rozwiązaniami układów nierówności z jedną niewiadomą są różne zbiory liczbowe. Te zestawy mają nazwy. Zatem na osi liczb zbiór liczb x taki, że \(-2 \leq x \leq 3 \) jest reprezentowany przez odcinek o końcach w punktach -2 i 3.
| -2 | 3 |
Jeśli \(a jest segmentem i jest oznaczone przez [a; b]
Jeśli \(a jest przedziałem i jest oznaczone przez (a; b)
Zbiory liczb \(x\) spełniające nierówności \(a \leq x są półprzedziałami i są oznaczone odpowiednio [a; b) i (a; b]
Nazywa się segmenty, przedziały, półprzedziały i półproste przedziały numeryczne.
Zatem przedziały liczbowe można określić w postaci nierówności.
Rozwiązaniem nierówności z dwiema niewiadomymi jest para liczb (x; y), która zamienia daną nierówność w rzeczywistą nierówność liczbową. Rozwiązanie nierówności polega na znalezieniu zbioru wszystkich jej rozwiązań. Zatem rozwiązaniami nierówności x > y będą np. pary liczb (5; 3), (-1; -1), ponieważ \(5 \geq 3 \) i \(-1 \geq - 1\)
Rozwiązywanie układów nierówności
Nauczyłeś się już, jak rozwiązywać nierówności liniowe z jedną niewiadomą. Czy wiesz co to jest układ nierówności i rozwiązanie tego układu? Dlatego proces rozwiązywania układów nierówności z jedną niewiadomą nie sprawi Ci żadnych trudności.
A jednak przypomnijmy: aby rozwiązać układ nierówności, należy rozwiązać każdą nierówność z osobna, a następnie znaleźć przecięcie tych rozwiązań.
Przykładowo pierwotny układ nierówności został zredukowany do postaci:
$$ \left\(\begin(array)(l) x \geq -2 \\ x \leq 3 \end(array)\right. $$
Aby rozwiązać ten układ nierówności, zaznacz rozwiązanie każdej nierówności na osi liczbowej i znajdź ich przecięcie:
| -2 | 3 |
Przecięcie to odcinek [-2; 3] - jest to rozwiązanie pierwotnego układu nierówności.
Informacje wstępne
Definicja 1
Nierówność postaci $f(x) >(≥)g(x)$, w której $f(x)$ i $g(x)$ są całkowitymi wyrażeniami wymiernymi, nazywa się całą nierównością wymierną.
Przykładami całych nierówności wymiernych są nierówności liniowe, kwadratowe i sześcienne z dwiema zmiennymi.
Definicja 2
Wartość $x$, przy której spełniona jest nierówność z definicji $1$, nazywa się pierwiastkiem równania.
Przykład rozwiązania takich nierówności:
Przykład 1
Rozwiąż całą nierówność $4x+3 >38-x$.
Rozwiązanie.
Uprośćmy tę nierówność:
Otrzymaliśmy nierówność liniową. Znajdźmy jego rozwiązanie:
Odpowiedź: $(7,∞)$.
W tym artykule rozważymy następujące metody rozwiązywania całych nierówności racjonalnych.
Metoda faktoryzacji
Metoda ta będzie następująca: Zapisuje się równanie w postaci $f(x)=g(x)$. Równanie to sprowadza się do postaci $φ(x)=0$ (gdzie $φ(x)=f(x)-g(x)$). Następnie funkcja $φ(x)$ jest rozkładana na czynniki przy użyciu minimalnych możliwych potęg. Obowiązuje zasada: Iloczyn wielomianów jest równy zero, gdy jeden z nich jest równy zero. Następnie na osi liczbowej zaznacza się znalezione pierwiastki i konstruuje krzywą znaku. W zależności od znaku początkowej nierówności zapisuje się odpowiedź.
Oto przykłady rozwiązań w ten sposób:
Przykład 2
Rozwiąż przez faktoryzację. $y^2-9
Rozwiązanie.
Rozwiążmy równanie $y^2-9
Korzystając ze wzoru na różnicę kwadratów mamy
Stosując regułę, że iloczyn czynników jest równy zero, otrzymujemy pierwiastki: $3$ i $-3$.
Narysujmy krzywą znaków:
Ponieważ początkowa nierówność ma znak „mniej niż”, otrzymujemy
Odpowiedź: $(-3,3)$.
Przykład 3
Rozwiąż przez faktoryzację.
$x^3+3x+2x^2+6 ≥0$
Rozwiązanie.
Rozwiążmy następujące równanie:
$x^3+3x+2x^2+6=0$
Wyjmijmy z nawiasów wspólne czynniki z dwóch pierwszych wyrazów i dwóch ostatnich
$x(x^2+3)+2(x^2+3)=0$
Wyjmijmy wspólny czynnik $(x^2+3)$
$(x^2+3)(x+2)=0$
Korzystając z reguły, że iloczyn czynników jest równy zero, otrzymujemy:
$x+2=0 \ i \ x^2+3=0$
$x=-2$ i „bez korzeni”
Narysujmy krzywą znaków:
Ponieważ początkowa nierówność ma znak „większy lub równy”, otrzymujemy
Odpowiedź: $(-∞,-2]$.
Sposób wprowadzania nowej zmiennej
Metoda ta jest następująca: Napisz równanie w postaci $f(x)=g(x)$. Rozwiązujemy to w następujący sposób: wprowadzamy nową zmienną, aby otrzymać równanie, którego sposób rozwiązania jest już znany. Następnie rozwiązujemy go i wracamy do wymiany. Z niego znajdziemy rozwiązanie pierwszego równania. Następnie na osi liczbowej zaznacza się znalezione pierwiastki i konstruuje krzywą znaku. W zależności od znaku początkowej nierówności zapisuje się odpowiedź.
Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.
Gromadzenie i wykorzystywanie danych osobowych
Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią.
Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami.
Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać.
Jakie dane osobowe zbieramy:
- Kiedy składasz wniosek na stronie, możemy zbierać różne informacje, w tym Twoje imię i nazwisko, numer telefonu, adres e-mail itp.
Jak wykorzystujemy Twoje dane osobowe:
- Zebrane przez nas dane osobowe pozwala nam kontaktować się z Tobą i informować Cię o wyjątkowych ofertach, promocjach i innych wydarzeniach oraz nadchodzących wydarzeniach.
- Od czasu do czasu możemy wykorzystywać Twoje dane osobowe do wysyłania ważnych powiadomień i komunikatów.
- Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak przeprowadzanie audytów, analiza danych i różnych badań w celu ulepszenia świadczonych przez nas usług i przedstawienia rekomendacji dotyczących naszych usług.
- Jeśli bierzesz udział w losowaniu nagród, konkursie lub podobnej promocji, możemy wykorzystać podane przez Ciebie informacje w celu administrowania takimi programami.
Ujawnianie informacji osobom trzecim
Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim.
Wyjątki:
- Jeżeli jest to konieczne – zgodnie z prawem, procedurą sądową, postępowaniem sądowym i/lub na podstawie żądań publicznych lub żądań od agencje rządowe na terytorium Federacji Rosyjskiej – ujawnij swoje dane osobowe. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub odpowiednie ze względów bezpieczeństwa, egzekwowania prawa lub innych celów ważnych dla społeczeństwa.
- W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane dane osobowe odpowiedniej następczej stronie trzeciej.
Ochrona danych osobowych
Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem.
Szanowanie Twojej prywatności na poziomie firmy
Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności.
W artykule rozważymy rozwiązywanie nierówności. Powiemy Ci jasno o jak skonstruować rozwiązanie nierówności z jasnymi przykładami!
Zanim zajmiemy się rozwiązywaniem nierówności na przykładach, poznajmy podstawowe pojęcia.
Ogólne informacje o nierównościach
Nierówność to wyrażenie, w którym funkcje są połączone znakami relacji >, . Nierówności mogą być zarówno liczbowe, jak i dosłowne.
Nierówności z dwoma znakami stosunku nazywane są podwójnymi, z trzema - potrójnymi itp. Na przykład:
a(x) > b(x),
a(x) a(x) b(x),
a(x) b(x).
a(x) Nierówności zawierające znak > lub lub - nie są ścisłe.
Rozwiązanie nierówności jest dowolną wartością zmiennej, dla której ta nierówność będzie prawdziwa.
"Rozwiąż nierówność" oznacza, że musimy znaleźć zbiór wszystkich jego rozwiązań. Są różne metody rozwiązywania nierówności. Dla rozwiązania nierówności Używają osi liczbowej, która jest nieskończona. Na przykład, rozwiązanie nierówności x > 3 to przedział od 3 do +, a liczba 3 nie jest wliczona w ten przedział, dlatego punkt na prostej jest oznaczony pustym okręgiem, ponieważ nierówność jest ostra. +
Odpowiedź będzie brzmiała: x (3; +).
Wartość x=3 nie jest uwzględniona w zestawie rozwiązań, dlatego nawias jest okrągły. Znak nieskończoności zawsze się wyróżnia nawias. Znak oznacza „przynależność”.
Przyjrzyjmy się, jak rozwiązać nierówności na innym przykładzie ze znakiem:
x 2
-+
Wartość x=2 jest zawarta w zbiorze rozwiązań, zatem nawias ma kształt kwadratu, a punkt na prostej zaznaczony jest wypełnionym okręgiem.
Odpowiedź będzie brzmieć: x. Wykres zestawu rozwiązań pokazano poniżej. ![]()
Podwójne nierówności
Kiedy dwie nierówności są połączone słowem I, Lub, następnie powstaje podwójna nierówność. Podwójna nierówność, np
-3
I 2x + 5 ≤ 7
zwany połączony, bo używa I. Wpis -3 Nierówności podwójne można rozwiązać stosując zasady dodawania i mnożenia nierówności.
Przykład 2 Rozwiąż -3 Rozwiązanie Mamy
Zbiór rozwiązań (x|x ≤ -1 Lub x > 3). Rozwiązanie możemy również zapisać, korzystając z notacji przedziałowej i symbolu wspomnienia lub włączając oba zbiory: (-∞ -1] (3, ∞) Wykres zbioru rozwiązań pokazano poniżej. 
Aby to sprawdzić, wykreślmy y 1 = 2x - 5, y 2 = -7 i y 3 = 1. Zauważ, że dla (x|x ≤ -1 Lub x > 3), y 1 ≤ y 2 Lub y 1 > y 3 . 
Nierówności o wartości bezwzględnej (moduł)
Nierówności czasami zawierają moduły. Do ich rozwiązania wykorzystywane są następujące właściwości.
Dla a > 0 i wyrażenia algebraicznego x:
|x| |x| > a jest równoważne x lub x > a.
Podobne stwierdzenia dla |x| ≤ a i |x| ≥ a.
Na przykład,
|x| |y| ≥ 1 odpowiada y ≤ -1 Lub y ≥ 1;
i |2x + 3| ≤ 4 odpowiada -4 ≤ 2x + 3 ≤ 4.
Przykład 4 Rozwiąż każdą z poniższych nierówności. Narysuj zbiór rozwiązań.
a) |3x + 2| b) |5 - 2x| ≥ 1
Rozwiązanie
a) |3x + 2|

b) |5 - 2x| ≥ 1
Zbiór rozwiązań to (x|x ≤ 2 Lub x ≥ 3) lub (-∞, 2] )
 Chronologia geologiczna Metoda paleontologiczna opiera się na badaniu organizmów kopalnych i roślin zakopanych w warstwach skalnych
Chronologia geologiczna Metoda paleontologiczna opiera się na badaniu organizmów kopalnych i roślin zakopanych w warstwach skalnych Mity na temat kreatywności, które okazały się nieprawdziwe, a mimo to zatruwały nasze życie
Mity na temat kreatywności, które okazały się nieprawdziwe, a mimo to zatruwały nasze życie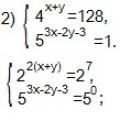 Rozwiązywanie równań i nierówności wykładniczych
Rozwiązywanie równań i nierówności wykładniczych