Zastosowanie teorii grafów w różnych dziedzinach działalności. Zastosowanie wykresów
Początki teorii grafów jednomyślnie przypisuje się rokowi 1736, kiedy to L. Euler rozwiązał popularne wówczas zagadnienie mostów królewieckich. Jednak wynik ten pozostał jedynym wynikiem teorii grafów przez ponad sto lat. Dopiero w połowie XIX wieku inżynier elektryk G. Kirchhoff opracował teorię drzew do badania obwodów elektrycznych, a matematyk A. Cayley w związku z opisem budowy węglowodorów rozwiązał problemy wyliczeniowe dla trzech rodzaje drzew.
Zrodzona z rozwiązywania zagadek i zabawnych gier (problemy o rycerzu szachowym, o królowych, „podróżach dookoła świata”, problemach związanych ze ślubami i haremami itp.), teoria grafów stała się obecnie prostym, dostępnym i potężnym sposobem rozwiązywania problemów związanych na szeroką gamę problemów. Wykresy są dosłownie wszechobecne. W formie wykresów można np. interpretować mapy drogowe i obwody elektryczne, mapy geograficzne i molekuły związki chemiczne, powiązania między ludźmi i grupami ludzi. W ciągu ostatnich czterdziestu lat teoria grafów stała się jedną z najszybciej rozwijających się dziedzin matematyki. Jest to spowodowane wymaganiami szybko rozwijającego się obszaru zastosowań. Znajduje zastosowanie w projektowaniu układów scalonych i obwodów sterujących, w badaniu automatów, obwodów logicznych, schematów blokowych programów, w ekonomii i statystyce, chemii i biologii, w teorii planowania. Metody matematyczne w dużej mierze przenikają obecnie naukę i technologię poprzez teorię grafów.
W artykule tym nie badamy właściwych problemów teorii grafów, ale tego, w jaki sposób można ją wykorzystać na szkolnych zajęciach z geometrii.
Zatem aktualność tematu badawczego wynika z jednej strony z popularności wykresów i związanych z nimi metod badawczych, które organicznie przenikają do świata różne poziomy prawie cała współczesna matematyka, a z drugiej strony nie opracowano całościowego systemu jej realizacji na kursie geometrii.
Celem pracy jest zbadanie zastosowania wykresów na szkolnych zajęciach z geometrii.
Przedmiotem jest proces nauczania geometrii.
Przedmiot – zajęcia lekcyjne i zajęcia pozalekcyjne
Cele: 1) określenie istoty i treści wykorzystania wykresów na szkolnych zajęciach z geometrii;
2) opracować PMC do prowadzenia lekcji geometrii w klasach 7-9.
Tematem wiodącym jest budowa modelu grafowego do dowodzenia twierdzeń geometrycznych.
Podstawa teoretyczna:
1. Teoria grafów, która powstała w 1736 r. (Leonard Euler (1708-1783), szybko się rozwinęła i pozostaje aktualna do dziś, ponieważ w życie codzienne Coraz częściej stosowane są ilustracje graficzne, przedstawienia geometryczne oraz inne techniki i metody wizualizacji.
1. Teoria grafów znajduje zastosowanie w różnych obszarach współczesnej matematyki i jej licznych zastosowaniach (Lipatow E. P.)
2. Teorię grafów wykorzystuje się w takich dziedzinach matematyki jak logika matematyczna, kombinatoryka itp.
Teoretyczne znaczenie pracy polega na:
Identyfikacja obszarów zastosowań teorii grafów;
Wykorzystanie teorii grafów do badania twierdzeń i problemów geometrycznych;
Praktyczne znaczenie pracy polega na wykorzystaniu wykresów w dowodzeniu twierdzeń geometrycznych i rozwiązywaniu problemów.
W wyniku tej pracy powstało:
Oprogramowanie i kompleks metodologiczny do prowadzenia lekcji geometrii w klasach 7-9.
Najtrudniejszą rzeczą w znalezieniu rozwiązania problemu jest ustalenie łańcucha logicznych konsekwencji prowadzących do sprawdzonego stwierdzenia. Aby kompetentnie rozumować logicznie, konieczne jest rozwinięcie umiejętności takiego myślenia, które pomogłoby w budowaniu odmiennych faktów geometrycznych w logiczne relacje.
W rozwijaniu umiejętności kultury myślenia szczególną rolę odgrywają formy wypowiedzi pisanej uczniów. Pisemne formy pracy są najważniejszym rodzajem zajęć rozwijających stabilne umiejętności logicznego rozumowania przy dowodzeniu twierdzeń i rozwiązywaniu problemów. Forma zapisu warunków zadania, rozsądne skróty i zapisy w obliczeniach oraz dowody problemów dyscyplinują myślenie i sprzyjają widzeniu geometrycznemu. Jak wiadomo, wzrok rodzi myślenie. Powstaje problem: jak ustalić logiczne powiązania pomiędzy odmiennymi faktami geometrycznymi i jak ułożyć je w jedną całość. Metoda diagramów grafowych pozwala na obserwację postępu w udowadnianiu twierdzeń i rozwiązywaniu problemów, co sprawia, że dowód jest bardziej wizualny oraz pozwala na krótkie i dokładne przedstawienie dowodów twierdzeń oraz rozwiązywanie problemów.
Wykorzystywany jest do tego wykres drzewa.
Wierzchołki „drzewa” (warunki twierdzenia lub problemu oraz kolejność spójników logicznych) przedstawiają prostokąty z umieszczonymi w nich informacjami, które następnie łączy się strzałkami. Na końcu diagramu znajduje się stwierdzenie, które należy udowodnić. Opisana forma dowodzenia twierdzeń i rozwiązywania problemów jest przydatna i wygodna dla studentów, ponieważ pozwala łatwo zidentyfikować główne etapy dowodzenia twierdzeń i rozwiązywania problemu.
Część badawcza.
Rozdział 1. Studium historii powstania teorii grafów.
Za twórcę teorii grafów uważa się matematyka Leonharda Eulera (1707-1783). Historię tej teorii można prześledzić poprzez korespondencję wielkiego naukowca. Oto tłumaczenie tekstu łacińskiego, które pochodzi z listu Eulera do włoskiego matematyka i inżyniera Marinoniego, wysłanego z Petersburga 13 marca 1736 roku.
„Kiedyś zadano mi problem dotyczący wyspy położonej w Królewcu i otoczonej rzeką, przez którą przerzucono siedem mostów. Pytanie brzmi, czy można je okrążyć w sposób ciągły, przechodząc tylko raz przez każdy most. I tak poinformowałem, że nikt mi do tej pory nie potrafił tego zrobić, ale nikt nie udowodnił, że jest to niemożliwe. To pytanie, choć banalne, wydało mi się godne uwagi, gdyż ani geometria, ani algebra, ani sztuka kombinatoryczna nie są do tego wystarczające. rozwiązać go. Po długim namyśle znalazłem prostą regułę opartą na całkowicie przekonującym dowodzie, za pomocą której we wszystkich tego typu zadaniach można od razu określić, czy taki objazd można wykonać przez dowolną liczbę zlokalizowanych mostów. w jakikolwiek sposób, lub czy nie da się zlokalizować mostów Królewca, aby można je było przedstawić na poniższym rysunku, na którym A oznacza wyspę, a B, C i D części kontynentu oddzielone od siebie odgałęzieniami. rzeka Siedem mostów oznaczono literami a, b, c, d, e, f, g.
Euler napisał o odkrytej przez siebie metodzie rozwiązywania tego rodzaju problemów
„To rozwiązanie ze swej natury najwyraźniej ma niewiele wspólnego z matematyką i nie rozumiem, dlaczego należy oczekiwać tego rozwiązania od matematyka, a nie od jakiejkolwiek innej osoby, gdyż decyzja ta jest poparta samym rozumowaniem i nie ma żadnych podstaw” trzeba zaangażować, aby znaleźć to rozwiązanie, istnieją jakieś prawa nieodłącznie związane z matematyką, więc nie wiem, jak się okazuje, że problemy, które mają niewiele wspólnego z matematyką, są częściej rozwiązywane przez matematyków niż przez innych.
Czy zatem można ominąć mosty Królewca, przechodząc tylko raz przez każdy z tych mostów? Aby znaleźć odpowiedź, kontynuujmy list Eulera do Marinoniego:
„Pytanie polega na ustaleniu, czy da się ominąć wszystkie te siedem mostów, przechodząc przez każdy tylko raz, czy nie. Moja reguła prowadzi do następującego rozwiązania tego problemu. Przede wszystkim trzeba sprawdzić, ile odcinków są oddzielone wodą - takie, które nie mają innego przejścia od siebie niż przez most. W tym przykładzie są cztery takie sekcje - A, B, C, D. Następnie trzeba rozróżnić, czy liczba liczba mostów prowadzących do tych poszczególnych odcinków jest parzysta lub nieparzysta. Czyli w naszym przypadku pięć mostów prowadzi do odcinka A, a każdy z trzech mostów prowadzi do pozostałych, czyli liczba mostów prowadzących do poszczególnych odcinków jest nieparzysta i tylko to jest. wystarczy, aby rozwiązać problem. Po ustaleniu tego stosujemy następującą zasadę: gdyby liczba mostów prowadzących do poszczególnych odcinków była parzysta, wówczas dany objazd byłby możliwy, a jednocześnie byłby możliwy. rozpocznij ten objazd od dowolnej sekcji. Jeśli dwie z tych liczb byłyby nieparzyste, bo tylko jedna nie może być nieparzysta, wówczas nawet wtedy przejście mogłoby zostać zakończone zgodnie z zaleceniami, ale z pewnością należy wziąć tylko początek objazdu. jeden z tych dwóch odcinków, do których prowadzi nieparzysta liczba mostów. Gdyby w końcu istniały więcej niż dwa odcinki, do których prowadzi nieparzysta liczba mostów, wówczas taki ruch byłby w ogóle niemożliwy; gdyby można było tu postawić inne, poważniejsze problemy, metoda ta mogłaby być jeszcze bardziej korzystna i powinna nie daj się zaniedbywać.”
Uzasadnienie powyższej zasady można znaleźć w liście L. Eulera do jego przyjaciela Ehlera z dnia 3 kwietnia tego samego roku. Poniżej przytaczamy fragment tego listu.
Matematyk napisał, że przejście jest możliwe, jeśli w rozwidleniu rzeki znajdują się nie więcej niż dwa obszary, do których prowadzi nieparzysta liczba mostów. Aby łatwiej to sobie wyobrazić, usuniemy na rysunku mosty, które już przebyliśmy. Łatwo sprawdzić, że jeśli zaczniemy poruszać się zgodnie z prawami Eulera, przejdziemy przez jeden most i go wymażemy, to na rysunku pojawi się odcinek, na którym znowu nie będą więcej niż dwa obszary, do których prowadzi nieparzysta liczba mostów, a jeśli tam to obszary z nieparzystą liczbą mostów, w jednym z nich będziemy się znajdować. Idąc dalej w ten sposób, przejdziemy raz wszystkie mosty.
Historia mostów miasta Królewca ma współczesną kontynuację.
Problem Na jeziorze znajduje się siedem wysp, które są ze sobą połączone w sposób pokazany na rysunku 2. Na którą wyspę należy zabrać łódkę podróżnych, aby mogli przepłynąć każdy most i tylko raz? Dlaczego podróżnych nie można przewieźć na wyspę A?
Rozwiązanie. Ponieważ problem ten jest podobny do problemu mostów w Królewcu, przy jego rozwiązywaniu skorzystamy także z reguły Eulera. W rezultacie otrzymujemy następującą odpowiedź: łódź musi zabrać podróżnych na wyspę E lub F, aby mogli raz przepłynąć każdy most. Z tej samej reguły Eulera wynika, że wymagany objazd jest niemożliwy, jeśli zaczyna się od wyspy A.
Następnie Koenig (1774–1833), Hamilton (1805–1865) i współcześni matematycy C. Berge, O. Ore, A. Zykov pracowali nad wykresami.
Historycznie rzecz biorąc, teoria grafów powstała ponad dwieście lat temu w procesie rozwiązywania zagadek. Przez bardzo długi czas znajdowała się na uboczu głównych kierunków badań naukowych, w królestwie matematyki zajmowała pozycję Kopciuszka, którego talenty w pełni ujawniły się dopiero wtedy, gdy znalazła się w centrum uwagi ogółu.
Pierwsza praca z zakresu teorii grafów, której właścicielem był słynny szwajcarski matematyk L. Euler, ukazała się w roku 1736. Impuls do rozwoju teorii grafów otrzymała na przełomie XIX i XX w., kiedy to liczba prac z zakresu topologii i kombinatoryki , z którym jest ściśle związany, gwałtownie wzrosło pokrewieństwo. Wykresy zaczęto wykorzystywać przy konstruowaniu schematów obwodów elektrycznych i obwodów molekularnych. Jako odrębna dyscyplina matematyczna teoria grafów została po raz pierwszy zaprezentowana w pracach węgierskiego matematyka Koeniga w latach 30. XX wieku.
Ostatnio wykresy i powiązane z nimi metody badawcze organicznie przeniknęły prawie całą współczesną matematykę na różnych poziomach. Teorię grafów uważa się za jedną z gałęzi topologii; jest to również bezpośrednio związane z algebrą i teorią liczb. Wykresy są skutecznie wykorzystywane w teorii planowania i kontroli, teorii harmonogramu, socjologii, językoznawstwie matematycznym, ekonomii, biologii, medycynie i geografii. Wykresy są szeroko stosowane w takich dziedzinach jak programowanie, teoria maszyn skończonych, elektronika, rozwiązywanie problemów probabilistycznych i kombinatorycznych, najkrótsza odległość itp. Rozrywka matematyczna i łamigłówki są również częścią teorii grafów. Teoria grafów szybko się rozwija i znajduje nowe zastosowania.
Rozdział 2. Podstawowe typy, pojęcia i struktura grafów.
Teoria grafów jest dyscypliną matematyczną stworzoną wysiłkiem matematyków, dlatego też jej prezentacja zawiera niezbędne ścisłe definicje.
Wykres to zbiór skończonej liczby punktów, zwanych wierzchołkami grafu, oraz linii łączących niektóre z tych wierzchołków w pary, zwanych krawędziami lub łukami grafu.
Lp. Nazwa wykresu Definicja Rysunek Przykład wykorzystania tego typu wykresu
1 Wykres zerowy Nieprzynależące do siebie wierzchołki grafu. Zadanie: Arkady, Borys. Władimir, Grigorij i Dmitry wymienili uściski dłoni na spotkaniu; każdy z nich raz uścisnął sobie dłonie. Ile jest krawędzi, nazywa się je izolowanymi. uściski dłoni zostały zrobione? Sytuacją odpowiadającą momentowi, w którym nie doszło jeszcze do uścisku dłoni, jest układ kropek pokazany na rysunku.
Graf składający się tylko z izolowanych wierzchołków nazywa się grafem zerowym.
Notacja: O” – graf z wierzchołkami i bez krawędzi
2 Grafy pełne Graf, w którym każda para wierzchołków ma każdą parę wierzchołków Należy pamiętać, że jeśli kompletny graf ma n wierzchołków, to liczba krawędzi będzie równa. Wszystkie uściski dłoni zostały zakończone.
Oznaczenie: U” – wykres składający się z n 10.
wierzchołki i krawędzie łączące wszystkie możliwe pary tych wierzchołków. Taki wykres można przedstawić jako n-gon, w którym narysowane są wszystkie przekątne
3 Niekompletne wykresy Wykresy, w których nie zostały jeszcze zakończone wszystkie uściski dłoni, uściski dłoni A i B, A i D, D oraz możliwe krawędzie zostały potrząśnięte, nazywane są niekompletnymi G, C i D.
4 Ścieżka na wykresie. Cykl. Ścieżka na wykresie z jednego wierzchołka do drugiego. W punkcie A znajduje się garaż dla pługu śnieżnego. Kierowca samochodu został wezwany do odśnieżania ulic widocznej na zdjęciu części miasta. Czy może mieć ciąg krawędzi, wzdłuż których będzie mógł zakończyć pracę na skrzyżowaniu, na którym znajduje się garaż, skoro kierowca może przejechać każdą ulicą pomiędzy tymi ulicami w swoim fragmencie miasta tylko raz?
szczyty.
W takim przypadku żadna krawędź trasy nie powinna pojawiać się więcej niż raz. Wierzchołek, z Jest to niemożliwe, ponieważ mówi się, że zamknięta ścieżka przechodząca przez wszystkie krawędzie grafu i wzdłuż której wytyczona jest trasa istnieje dla każdej krawędzi tylko raz, jeśli stopnie wszystkich wierzchołków grafu są parzyste.
początek ścieżki, szczyt na końcu trasy -
koniec drogi. Cykl to ścieżka, na której rysunek przedstawia za pomocą wykresu schemat dróg pomiędzy obszarami zaludnionymi, których początek i koniec pokrywają się. W prostych punktach.
cykl to cykl, który nie przechodzi. Przykładowo z punktu A (wierzchołek wykresu) do punktu H można dojść różnymi drogami: ADGH, AEH, AEFCEH, ABCEH.
przez jeden z wierzchołków grafu więcej niż jeden. Czym różni się trasa AEH od trasy AEFCEH?
czasy. Bo na drugiej trasie dwukrotnie odwiedziliśmy „skrzyżowanie” w punkcie E.
Ta trasa jest dłuższa niż AEH. Trasę AEH można uzyskać z trasy
Jeżeli cykl obejmuje wszystkie krawędzie AEFCEH, należy „przekreślić” trasę FCE od ostatniej.
wykresie raz na raz, to taki cykl Trasa AEH jest ścieżką na wykresie, ale trasa AEFCEH nie jest ścieżką.
zwaną linią Eulera.
Połączone i rozłączone wykresy. Zadanie 1: Czy z drutu o długości 12 dm można wykonać ramę sześcianu o długości krawędzi
Czy dwa wierzchołki grafu nazywamy połączonymi, o długości 1 dm, bez rozbijania drutu na kawałki?
jeśli w grafie istnieje ścieżka, która kończy się w tych wierzchołkach. Jeśli taka ścieżka nie istnieje, mówimy, że wierzchołki nie są połączone.
Ponieważ ścieżka przechodząca wzdłuż wszystkich krawędzi grafu i wzdłuż każdej krawędzi tylko raz, istnieje tylko w następujących przypadkach:
1) gdy stopień każdego wierzchołka jest parzysty (ścieżka jest zamknięta)
2) gdy istnieją tylko dwa wierzchołki o nieparzystym stopniu.
Definicja 2:
Graf nazywamy spójnym, jeśli dowolna para jego wierzchołków jest spójna.
Graf nazywamy rozłączonym, jeśli ma co najmniej jedną rozłączoną parę wierzchołków.
6 Drzewa Drzewem jest dowolny graf spójny, Załącznik nr 1. Drzewo genealogiczne Zholmurzaevy Tomiris.
najfatalniejszy. Niepołączony graf składający się wyłącznie z drzew nazywa się lasem.
7 Wykresy izomorficzne. Wykresy pokazane na rysunku dostarczają tych samych informacji. Takie wykresy nazywane są izomorficznymi (identycznymi).
8 Pojęcie wykresu planarnego Wykres, który można przedstawić w zadaniu. Trzy samoloty mieszkają w trzech różnych domach, a sąsiedzi pokłócili się między sobą. Niedaleko ich domów, w miejscu przecięcia się jej żeber, znajdują się trzy studnie. Czy możliwe jest, aby tylko na szczytach, zwanych każdym domem, położyć płasko do każdej ze studni. ścieżkę, aby żadne z nich się nie przecinały?
Rozwiązanie: Po narysowaniu ośmiu ścieżek możesz upewnić się, że nie jest możliwe narysowanie dziewiątej, która nie przecina się z żadną z wcześniej narysowanych ścieżek.
Skonstruujmy graf, którego wierzchołki
A, B, C, 1, 2, 3
warunki zadania odpowiadają domom i studniom, a my postaramy się udowodnić, że dziewiątej ścieżki - krawędzi grafu, która nie przecina pozostałych krawędzi - nie można narysować.
Krawędzie narysowane na wykresie na rysunku
A1, A2, A3 i B1, B2, VZ (odpowiadające ścieżkom z domów A i B do wszystkich studni).
Skonstruowany graf podzielił płaszczyznę na trzy obszary: X, Y, Z. Wierzchołek B w zależności od swojego położenia na płaszczyźnie należy do jednego z tych trzech obszarów. Jeśli weźmiesz pod uwagę każdy z trzech przypadków „uderzenia” w wierzchołek
B do jednego z obszarów X, Y lub Z, następnie upewnij się, że za każdym razem jeden z wierzchołków grafu wynosi 1, 2 lub 3
(jedna ze studzienek) będzie „niedostępna” dla wierzchołka B (tzn. nie będzie możliwości narysowania jednej z krawędzi B1, B2 lub B3, która nie przecinałaby krawędzi już istniejących na grafie).
Odpowiedź na pytanie problematyczne będzie brzmieć: „Nie!”
Grafy skierowane Krawędź grafu nazywamy krawędzią skierowaną, jeśli jeden z jej wierzchołków jest początkiem, a drugi końcem tej krawędzi.
Graf, w którym wszystkie krawędzie są skierowane, nazywa się grafem skierowanym.
Dokonałem więc przeglądu podstawowych pojęć teorii grafów, bez których nie byłoby możliwe dowodzenie twierdzeń, a co za tym idzie, rozwiązywanie problemów.
Wnioski z wykonanej pracy:
Nauczyłem się porządkować cały materiał informacyjny w formie tabeli;
Układ materiał teoretyczny przyczynić się do wizualnego zrozumienia rodzajów wykresów i ich zastosowania;
Pracowałem nad przykładami wykorzystania teorii grafów przy tworzeniu mojego drzewa genealogicznego.
Załącznik nr 1.
DRZEWO GENEOLOGICZNE
Zbuduj drzewo genealogiczne Zholmurzaevy Tomiris.
Metoda rozwiązania.
Graficzny sposób rozwiązania problemu.
Graficznym sposobem rozwiązania problemu jest narysowanie „drzewa warunków logicznych”. „Drzewo” wyraża w formie prostego rysunku logiczny związek między krewnymi. Każde pokolenie na drzewie odpowiada jednej gałęzi.
Jako przykład wziąłem swoje drzewo genealogiczne.
Rozdział 3. Zastosowanie teorii grafów.
Z wykresami spotykamy się częściej, niż jest to możliwe na pierwszy rzut oka. Przykładami grafów są dowolne mapy drogowe, schematy elektryczne, rysunki wielokątów itp. Przez długi czas uważano, że teoria grafów wykorzystywana jest głównie do rozwiązywania problemów logicznych. Podczas rozwiązywania problemów logicznych często trudno jest zapamiętać liczne warunki podane w zadaniu i ustalić powiązania między nimi. Wykresy pomagają w rozwiązywaniu takich problemów, umożliwiając wizualne przedstawienie zależności pomiędzy danymi problemu. Sama teoria grafów była uważana za część geometrii. Jednak w XX wieku szerokie zastosowania teorii grafów znaleziono w ekonomii, biologii, chemii, elektronice, planowanie sieci, kombinatoryki i innych dziedzin nauki i technologii. W rezultacie zaczęła się szybko rozwijać i przekształciła w niezależną teorię rozgałęzioną. Rozwiązanie wielu problemów matematycznych jest uproszczone, jeśli możliwe jest wykorzystanie wykresów. Prezentacja danych w formie wykresu ułatwia ich przejrzystość. Wiele dowodów jest również upraszczanych i staje się bardziej przekonujących, jeśli użyje się wykresów.
3. 1. Zastosowanie grafów w zagadnieniach i twierdzeniach geometrycznych.
Za pomocą wykresów można łatwo ustalić łańcuchy logicznych konsekwencji prowadzących do udowodnienia twierdzenia. Krótko i dokładnie przedstaw dowód twierdzenia i rozwiązanie problemu.
Udowodnić, że w trójkącie równoramiennym dwusieczne wyprowadzone z wierzchołków u podstawy są równe.
Metody rozwiązań.
Dowód problemu za pomocą rozumowania.
Niech ABC będzie trójkątem równoramiennym z
B1 A1 podstawa AB i dwusieczne AA1 i BB1.
Rozważmy ∆АВВ1 i ∆ВАА1. Mają ∟В1АВ=
∟A1BA jako kąty u podstawy trójkąta równoramiennego ∆ABC. ∟АВВ1= ∟А1АВ
A B, ponieważ AA1 i BB1 są dwusiecznymi kątów u podstawy trójkąta równoramiennego. AB to strona wspólna. Oznacza
∆АВВ1 = ∆ВАВ1 wzdłuż boku i dwóch sąsiednich kątów. Z równości trójkątów wynika, że ich boki AA1 i BB1 są równe.
Dowód problemu za pomocą wykresu.
Udowodnij: AA=BB
Używamy wykresu do rozumowania. Wierzchołki wykresu to warunki twierdzenia lub problemu oraz etapy dowodu.
Krawędzie wykresu są konsekwencjami logicznymi. Koniec wykresu jest stwierdzeniem dającym się udowodnić.
Kolor służy do podkreślenia komponentów. Twierdzenie i warunki problemu są zaznaczone na niebiesko. Udowodnione stwierdzenie jest czerwone. Etapy dowodu - czarne.
Opisana forma dowodzenia twierdzeń i rozwiązywania problemów jest przydatna i wygodna dla studentów, ponieważ pozwala wyróżnić główne etapy dowodzenia twierdzeń i rozwiązywania problemu.
3. 2. Kompleks programowo-metodologiczny.
a) Podręcznik nauczyciela.
Proponowany podręcznik został opracowany zgodnie z podręcznikiem geometrii dla klas 7-9 autorstwa A.V. Jego głównym celem jest wyposażenie procesu studiowania geometrii w niezbędne pomoce wizualne, pomoc nauczycielowi w nauczaniu geometrii: ułatwienie procesu dowodzenia twierdzeń, opanowanie materiału teoretycznego w procesie rozwiązywania problemów. Diagramy grafowe mają charakter wieloaspektowy i w zależności od celów i form zajęć mogą być wykorzystywane na różne sposoby: ilustracyjne, mające na celu zwiększenie przejrzystości przy wyjaśnianiu nowego materiału teoretycznego, przy uogólnianiu i systematyzowaniu nowego materiału (diagramy z twierdzeniami); jako karty wykorzystywane przy prowadzeniu ankiet indywidualnych i frontalnych (diagramy z zadaniami). Do podręcznika dołączono zeszyt ćwiczeń dla ucznia. Do porządkowania można wykorzystać skoroszyt niezależna praca uczniów w czasie zajęć lekcyjnych i po ich zakończeniu.
b) Zeszyt ćwiczeń dla uczniów.
Podręcznik sporządzono w formie zeszytu ćwiczeń. Podręcznik zawiera 28 wykresów z twierdzeniami i 28 wykresów z zadaniami. Diagramy graficzne zawierają główny materiał programu, który jest przedstawiony z niezbędną przejrzystością i przedstawia ramy rozwiązania. Uczniowie kolejno wypełniają puste komórki informacjami, które składają się na rozwiązanie problemu.
Kolor służy do podkreślenia komponentów. Warunki twierdzenia i problemu są zaznaczone na niebiesko, twierdzenie do udowodnienia na czerwono, etapy dowodu na czarno.
Podręcznik jest przydatny dla uczniów klas 7-9.
c) Instrukcja elektroniczna.
Wyniki pracy i ich dyskusja. Projekt jest wynikiem dwuletnich badań nad wykorzystaniem wykresów w szkolnych lekcjach matematyki.
Tworzenie programowo – kompleks metodologiczny a jego realizacja odbywała się w okresie:
Prowadzenie zajęć dla klubu Arystoteles na temat „Rozwiązywanie problemów logicznych za pomocą grafów”.
Zastosowanie grafów w dowodach twierdzeń i problemów geometrycznych
Na lekcjach geometrii w klasach 8 i 9.
Prezentacje z projektem w szkole naukowe i praktyczne konferencje.
WNIOSEK.
Podsumowując wyniki badań nad wykorzystaniem wykresów na szkolnym kursie geometrii, doszedłem do następującego wniosku:
1. Przewaga grafowego dowodu twierdzeń i rozwiązywania problemów nad tradycyjnym polega na zobrazowaniu dynamiki dowodu twierdzeń i problemów.
2. Wprowadzenie w proces dowodzenia twierdzeń geometrycznych i problemów metody grafów-schematów pozwala udoskonalić umiejętności konstruowania dowodu.
3. Opracowano oprogramowanie i kompleks metodyczny do nauki geometrii w klasach 7-9: a) podręcznik nauczyciela; b) zeszyt ćwiczeń dla studentów; c) podręcznik w wersji elektronicznej jest przydatny dla uczniów klas 7-9.
Wydanie edukacyjne
Yuyukin Nikołaj Aleksiejewicz
LR nr. Podpisano do pieczęci
Uch. wyd. l.. , .
Państwowy Uniwersytet Techniczny w Woroneżu
394026 Woroneż, Moskovsky Avenue. 14
KATALOG DYSKÓW MAGNETYCZNYCH
Katedra Matematyki Wyższej i Modelowania Fizycznego i Matematycznego
nie dotyczy Yuyukin
MATEMATYKA DYSKRETNA Część 1. Elementy teorii grafów
Seminarium
nie dotyczy Yuyukin
MATEMATYKA DYSKRETNA Część 1. Elementy teorii grafów
Seminarium
Woroneż 2004
WSTĘP
Podręcznik ten może być wykorzystany na kursie „Matematyka dyskretna” przez studentów VSTU studiujących na następujących specjalnościach:
090102 – Bezpieczeństwo komputerowe;
090105 – Kompleksowe zapewnienie bezpieczeństwa informacji systemów zautomatyzowanych;
090106 - Bezpieczeństwo informacji systemów telekomunikacyjnych.
Dyscyplina „Matematyka Dyskretna” zapewnia zdobywanie wiedzy i umiejętności zgodnie z państwowym, ogólnym standardem edukacyjnym, a jednocześnie przyczynia się do zdobywania edukacja podstawowa, kształtowanie światopoglądu i rozwój logicznego myślenia.
Teoria grafów jest skutecznym narzędziem do formalizowania współczesnych problemów inżynierskich związanych z obiektami dyskretnymi. Stosowany jest w projektowaniu układów scalonych i obwodów sterujących, badaniu automatów i obwodów logicznych, w analiza systemu, zautomatyzowana kontrola produkcji, rozwój sieci komputerowych i informacyjnych, projektowanie obwodów i projektowanie topologiczne itp.
W podręcznik zarysowuje podstawy, podstawowe metody i algorytmy teorii grafów. Tutaj prezentujemy n-grafy i dwuznaki; izomorfizmy; drzewa; wykresy Eulera; wykresy planarne; pokrycia i zestawy niezależne; silna łączność
V dwuznaki; Analiza wykresów łańcucha Markowa; algorytmy wyszukiwania najkrótszych ścieżek w grafach; Problem poszukiwania cykli Hamiltona
V wykres; problem komiwojażera; wyliczenie wykresów i map; ekstremalne zadania; problemy optymalizacyjne; zadania uniwersalne; metoda rozgałęziona i związana; a także rozwijać praktyczne umiejętności posługiwania się powyższymi koncepcjami.
Celem przedmiotu jest rozwinięcie wiedzy teoretycznej, umiejętności praktycznych i zdolności studentów w zakresie modelowania procesów i zjawisk w naukach przyrodniczych i technice.
ke, z umiejętnością posługiwania się symbolami matematycznymi do wyrażenia zależności ilościowych i jakościowych obiektów niezbędnych do wykonywania czynności służbowych w zakresie bezpieczeństwa informacji na wysokim poziomie zawodowym.
Osiągnięciu tego celu służą następujące zadania:
studiować możliwie najszerszy zakres koncepcji teorii grafów;
zdobyć umiejętności rozwiązywania problemów edukacyjnych i praktycznych;
główne metody optymalizacji;
rozwijać umiejętności stawiania i rozwiązywania problemów informacyjnych, modelowania i analizowania informacji za pomocą grafów.
Dyscyplina „Matematyka dyskretna” jest jedną z dyscyplin matematycznych stosowanych. Opiera się na wiedzy zdobytej przez studentów podczas studiowania dyscyplin „Algebra” oraz „Logika matematyczna i teoria algorytmów”. W badaniu wykorzystywana jest wiedza i umiejętności zdobyte podczas studiowania dyscypliny „Matematyka dyskretna”. ogólnie profesjonalista i dyscyplin specjalnych.
1. PODSTAWOWE POJĘCIA TEORII GRAFÓW.
1.1. Zagadnienia teorii grafów.
Teoria grafów to dziedzina matematyki badająca systemy połączeń między różnymi obiektami, podobnie jak ma to miejsce w przypadku koncepcji relacji. Jednak niezależna definicja wykresu upraszcza prezentację teorii i czyni ją bardziej zrozumiałą i wizualną.
Pierwsze problemy teorii grafów dotyczyły rozwiązywania problemów rozrywkowych i łamigłówek.
Pierwsze zadanie. Problem mostów królewieckich postawił i rozwiązał Euler w 1786 roku. Miasto położone było na brzegach i dwóch wyspach rzeki Pregoły. Wyspy były połączone między sobą a brzegami siedmioma mostami, jak pokazano na rysunku.
Pojawiło się pytanie: czy można wyjść z domu i wrócić, przechodząc przez każdy most dokładnie raz?
Drugie zadanie. Problem trzech domów i trzech studni. Są trzy domy i trzy studnie.
Wymagane jest narysowanie ścieżki z każdego domu do każdej studni, aby ścieżki się nie przecinały. Zadanie było

rozwiązany przez Pontriagina i niezależnie od niego przez Kuratowskiego w
Trzecie zadanie. Około czterech kolorów. Pokoloruj dowolną mapę na płaszczyźnie czterema kolorami, tak aby żadne dwa sąsiednie obszary nie były pomalowane tym samym kolorem.
Wiele wyników teorii grafów wykorzystuje się do rozwiązywania praktycznych problemów w nauce i technologii. Tak więc w połowie XIX wieku Kirchhoff wykorzystał teorię grafów do obliczenia złożonych obwodów elektrycznych. Jednak jako dyscyplina matematyczna teoria grafów ukształtowała się dopiero w latach 30. XX wieku. W tym przypadku wykresy są uważane za pewne abstrakcyjne obiekty matematyczne. Wykorzystuje się je w analizie i syntezie obwodów i systemów, w planowaniu i zarządzaniu siecią, badaniach operacyjnych, programowaniu, modelowaniu życia organizmu i innych obszarach.
1.2. Podstawowe definicje.
Graf G= (V,E) jest zbiorem dwóch zbiorów - niepustego zbioru wierzchołków V oraz zbioru nieuporządkowanych i uporządkowanych par wierzchołków E. W dalszej części rozważymy grafy skończone, tj. grafy o skończonym zbiorze wierzchołków i skończonej rodzinie par. Nieuporządkowaną parę wierzchołków nazywamy krawędzią, a uporządkowaną parę nazywamy łukiem.
Zazwyczaj graf jest reprezentowany przez diagram: wierzchołki to kropki (lub okręgi), krawędzie to linie o dowolnej konfiguracji. Strzałka dodatkowo wskazuje jego kierunek na łuku. Należy pamiętać, że przedstawiając wykres, przewoźnik

właściwości geometryczne żeber (długość, krzywizna), a także położenie względne wierzchołki na płaszczyźnie.
Wierzchołki nie należące do żadnej krawędzi (łuku) nazywane są izolowanymi. Wierzchołki połączone krawędzią lub łukiem nazywane są sąsiadującymi. Krawędź (łuk) i dowolny z jej dwóch wierzchołków nazywane są incydentami.
Mówią, że krawędź (u, v) łączy wierzchołki u i v, a łuk (u, v) zaczyna się w wierzchołku u i kończy się w wierzchołku v, przy czym u nazywa się początkiem, a v końcem tego łuku.
Para wierzchołków może być połączona dwiema lub większą liczbą krawędzi (łukami skierowanymi w tym samym kierunku). Takie krawędzie (łuki) nazywane są wielokrotnymi. Łuk (lub krawędź) może zaczynać się lub kończyć w tym samym wierzchołku. Taki łuk (krawędź) nazywa się pętlą. Wykres zawierający pętle nazywany jest pseudografem. Wykres mający wiele krawędzi (łuków) nazywany jest multigrafem.
Graf bez pętli i wielu krawędzi nazywa się prostym. Graf prosty nazywamy kompletnym, jeśli dla dowolnej pary jego wierzchołków istnieje łącząca je krawędź (łuk). Kompletny graf z n wierzchołkami jest oznaczony przez K n. Są to na przykład wykresy
Graf składający się z jednego izolowanego wierzchołka (K 1) nazywany jest trywialnym.
Dopełnieniem grafu G jest graf G, który ma te same wierzchołki co graf G i zawiera te krawędzie, które należy dodać do grafu G, aby otrzymać pełny graf.
Do każdego nie-dygrafa kanonicznie pasuje graf skierowany o tym samym zestawie wierzchołków, w którym każdą krawędź zastąpiono dwoma łukami padającymi na te same wierzchołki i mającymi przeciwne kierunki.
1.3. Stopnie wierzchołków grafu.
Stopień (wartościowość) (oznaczenie d (v) lub stopień (v)) wierzchołka v prostego grafu G to liczba krawędzi lub łuków padających na dany wierzchołek v. Przy obliczaniu wartościowości wierzchołków pseudografu każdą pętlę należy policzyć dwukrotnie.
Jeśli stopnie wszystkich wierzchołków n-grafu są równe k, wówczas graf nazywa się zwykły (jednolity) stopień k. Jeśli stopień wierzchołka wynosi 0, to jest on izolowany. Jeśli stopień wierzchołka wynosi 1, wówczas wierzchołek nazywa się wierzchołkiem końcowym (wiszący, ślepy zaułek).
W przypadku digrafu nazywa się liczbę łuków wychodzących z wierzchołka v
jest różny półstopień wyniku |
(v) i przychodzące – półetapowe |
|||||||||
nowe połączenie d |
(v), W tym przypadku relacja d (v)= |
|||||||||
(v)+ |
(v). |
|||||||||
Twierdzenie Eulera: Suma stopni wierzchołków grafu wynosi
podwoić liczbę żeber, tj.
d(vi)
(v) |
|||||||
Gdzie n jest liczbą wierzchołków; m – liczba
żebra (łuki). O tym twierdzeniu świadczy fakt, że przy obliczaniu sumy stopni wierzchołków każdą krawędź uwzględnia się dwukrotnie – dla jednego końca krawędzi i dla drugiego.
1.4. Izomorfizm wykresu.
Graf nazywa się oznakowanym (lub przenumerowanym), jeśli jego wierzchołki różnią się od siebie w jakiś sposób.
etykiety (liczby). Liczenie jest brane pod uwagę całkowicie dane w ścisłym tego słowa znaczeniu, jeżeli numeracja jego wierzchołków i krawędzi jest stała. W tym przypadku wykresy G 1 i G 2 nazywane są równymi (oznaczenie G 1 = G 2), jeśli ich zbiory wierzchołków i krawędzi pokrywają się. Nazywa się dwa wykresy lub pseudografy G 1 = (V 1 , E 1 ) i G 2 = (V 2 , E 2 )
izomorficzny (notacja G |
jeśli istnieją |
|||||
mapowania jeden do jednego: 1) |
: V 1 V 2 |
|||||
: E 1 E 2 tak, że dla dowolnych dwóch wierzchołków u, v w grafie |
||||||
relacja ((u, v)) ((u), (v)) jest ważna. |
||||||
Dwa proste wykresy (bez pętli i wielu krawędzi) G 1 |
i G2 |
|||||
okazują się izomorficzne, jeśli są wzajemnie identyczne
mapowanie wartości |
: V 1 V 2 |
No to co? |
(u, v) ((u), (v)). |
Zatem grafy różniące się jedynie numeracją wierzchołków i krawędzi są izomorficzne. Izomorfizm grafów jest relacją równoważności, ponieważ ma właściwości:
refleksyjność - |
G1, |
i bijekcja |
|||||||||||
jest identyczną funkcją. |
|||||||||||||
Symetria. |
z bijekcją |
||||||||||||
z bijekcją |
|||||||||||||
Przechodniość. |
G 1 G 2 |
bijekcja |
1, za |
||||||||||
z bijekcją |
następnie G.G |
z bijekcją |
|||||||||||
2 (1 ) .
Teoria grafów znajduje zastosowanie m.in. w systemach informacji geograficznej (GIS). Istniejące lub nowo projektowane domy, konstrukcje, bloki itp. traktowane są jako wierzchołki, a łączące je drogi, sieci użyteczności publicznej, linie energetyczne itp. traktowane są jako krawędzie. Wykorzystanie różnych obliczeń wykonywanych na takim wykresie pozwala np. znaleźć najkrótszą trasę objazdu, najbliższy sklep spożywczy lub zaplanować optymalną trasę.
Teoria grafów zawiera dużą liczbę nierozwiązanych problemów i jeszcze niepotwierdzonych hipotez.
Główne obszary zastosowań teorii grafów:
W chemii (do opisu struktur, ścieżek reakcji złożonych regułę fazową można również interpretować jako problem teorii grafów); Chemia obliczeniowa jest stosunkowo młodą dziedziną chemii opierającą się na zastosowaniu teorii grafów. Teoria grafów jest matematyczną podstawą chemoinformatyki. Teoria grafów umożliwia dokładne określenie liczby teoretycznie możliwych izomerów w węglowodorach i innych związkach organicznych;
W informatyce i programowaniu (wykres algorytmu);
W systemach komunikacyjnych i transportowych. W szczególności do przesyłania danych w Internecie;
W ekonomii;
W logistyce;
W projektowaniu obwodów (topologia połączeń elementów na płytce drukowanej lub mikroukładzie to wykres lub hipergraf).
Istnieje specjalny rodzaj wykresu, drzewo.Drzewo jest spójnym grafem acyklicznym. Powiązanie oznacza obecność ścieżek pomiędzy dowolną parą wierzchołków, acykliczność oznacza brak cykli oraz fakt, że pomiędzy parami wierzchołków istnieje tylko jedna ścieżka. NA Ryc. 1.3 przedstawione drzewo binarne.
Drzewo binarne- drzewiasta struktura danych, w której każdy węzeł ma nie więcej niż dwa potomkowie(dzieci). Zwykle nazywa się ten pierwszy węzeł nadrzędny i dzieci są nazywane lewy I prawi spadkobiercy.
Macierzowa reprezentacja wykresów. Matryca incydentów.
Rozwój algorytmicznych podejść do analizy właściwości grafów wymaga pewnych metod opisywania wykresów, które są bardziej odpowiednie do praktycznych obliczeń, w tym z wykorzystaniem komputera. Przyjrzyjmy się trzem najczęstszym sposobom przedstawiania wykresów.
Załóżmy, że wszystkie wierzchołki i wszystkie krawędzie grafu nieskierowanego lub wszystkie wierzchołki i wszystkie łuki (w tym pętle) grafu skierowanego są numerowane zaczynając od jednego. Graf (nieskierowany lub skierowany) można przedstawić w postaci macierzy typu , gdzie jest to liczba wierzchołków, a to liczba krawędzi (lub łuków). W przypadku grafu nieskierowanego elementy tej macierzy są określone w następujący sposób:
W przypadku grafu skierowanego elementy macierzy są określone w następujący sposób:

Macierz tak zdefiniowanego typu nazywa się macierz incydentów.
Przykład uzyskania macierzy incydentów. Dla wykresu pokazanego poniżej ( Ryż. 2.1 aRysunek 2.1 b).


Ryc. 2.1 a Ryc. 2.1 b
Macierz sąsiedztwa.
Pomimo tego, że przedstawienie wykresu w postaci macierzy zachorowań odgrywa bardzo ważną rolę w badaniach teoretycznych, w praktyce metoda ta jest bardzo nieskuteczna. Po pierwsze, macierz ma w każdej kolumnie tylko dwa niezerowe elementy, co sprawia, że ten sposób reprezentacji grafu jest nieekonomiczny, gdy liczba wierzchołków jest duża. Ponadto rozwiązywanie problemów praktycznych przy użyciu macierzy incydentów jest bardzo pracochłonne.
Oszacujmy np. koszty czasowe rozwiązania tak prostego problemu w grafie skierowanym za pomocą macierzy częstości: dla danego wierzchołka znajdź jego „otoczenie” – zbiór następników i zbiór poprzedników wierzchołka, czyli: zbiór wszystkich wierzchołków, z których jest bezpośrednio osiągalny, oraz zbiór wszystkich wierzchołków, z których jest on bezpośrednio osiągalny.
Aby rozwiązać to zadanie na macierzy częstości grafu skierowanego, należy podążać wzdłuż wiersza z liczbą, aż pojawi się element niezerowy (+1 lub –1). Jeśli zostanie wykryte +1, w odpowiedniej kolumnie musisz znaleźć wiersz, w którym zapisana jest liczba –1. Numer linii, w której występuje ta liczba, podaje numer wierzchołka bezpośrednio osiągalnego z tego wierzchołka. Jeśli zostanie wykryte -1, należy znaleźć wiersz w kolumnie zawierający 1 i uzyskać numer wierzchołka, z którego ten wierzchołek jest bezpośrednio dostępny. Aby uzyskać całe „środowisko”, należy wykonać określone wyszukiwanie wszystkich niezerowych elementów k-ta linia. Najbardziej czasochłonną procedurą jest znalezienie niezerowego elementu w kolumnie. Liczba takich procedur wyszukiwania jest równa stopniowi wierzchołka. W tym przypadku powiemy, że złożoność algorytmu analizy środowiska wierzchołka wynosi (porządek).
Można zauważyć, że poszukiwanie „otoczenia” wszystkich wierzchołków zajmie czas rzędu iloczynu liczby wierzchołków grafu skierowanego przez sumę stopni wszystkich wierzchołków, co jak można wykazać, jest proporcjonalna do liczby łuków grafu skierowanego. Zatem złożoność algorytmu wyszukiwania „środowiska” wynosi , tj. wyszukiwanie wymaga czasu rzędu iloczynu liczby wierzchołków i liczby łuków.
Bardziej wydajną strukturą macierzową reprezentującą wykres jest macierz sąsiedztwa wierzchołków, Lub Macierz Boole’a wykres. Jest to macierz kwadratowa rzędu B N, którego elementy są zdefiniowane w następujący sposób:
dla grafu nieskierowanego: ![]()
dla grafu skierowanego: ![]()
Dla wykresu pokazanego poniżej ( Ryż. 2.2 a) macierzą zachorowań będzie macierz przedstawiona na ( Rysunek 2.2 b).
Tekst pracy publikujemy bez obrazów i formuł.
Pełna wersja praca dostępna jest w zakładce „Pliki Pracy” w formacie PDF
„W matematyce nie należy pamiętać wzorów, ale proces myślenia…”
E. I. Ignatiew
Teoria grafów jest obecnie intensywnie rozwijającą się gałęzią matematyki. Wyjaśnia to fakt, że wiele obiektów i sytuacji opisano w formie modeli grafowych, co jest bardzo ważne dla normalnego funkcjonowania życia społecznego. To właśnie ten czynnik determinuje zasadność ich bardziej szczegółowych badań. Dlatego temat tej pracy jest dość istotny.
Cel praca badawcza: poznać cechy zastosowania teorii grafów w różnych dziedzinach wiedzy i rozwiązywaniu problemów logicznych.
Cel określił co następuje zadania:
zapoznać się z historią teorii grafów;
studiować podstawowe pojęcia teorii grafów i główne cechy grafów;
pokazać praktyczne zastosowanie teorii grafów w różnych dziedzinach wiedzy;
Rozważ sposoby rozwiązywania problemów za pomocą wykresów i twórz własne problemy.
Obiekt badania: sfera działalności człowieka dla zastosowania metody grafowej.
Przedmiot Badania: sekcja matematyki „Teoria grafów”.
Hipoteza. Stawiamy hipotezę, że nauka teorii grafów może pomóc uczniom w rozwiązywaniu problemów logicznych w matematyce, co będzie kształtować ich przyszłe zainteresowania.
Metody prace badawcze:
W trakcie naszych badań zastosowaliśmy następujące metody:
1) Praca z różnymi źródłami informacji.
2) Opis, zbiór, systematyzacja materiału.
3) Obserwacja, analiza i porównanie.
4) Przygotowanie zadań.
Znaczenie teoretyczne i praktyczne O pracy tej decyduje fakt, że wyniki mogą być wykorzystane w informatyce, matematyce, geometrii, rysunku i godziny lekcyjne, a także dla szerokiego grona czytelników zainteresowanych tą tematyką. Praca badawcza ma wyraźną orientację praktyczną, gdyż w pracy autor prezentuje liczne przykłady wykorzystania grafów w wielu dziedzinach wiedzy oraz formułuje własne zadania. Materiał ten można wykorzystać na fakultatywnych zajęciach z matematyki.
ROZDZIAŁ I TEORETYCZNY PRZEGLĄD MATERIAŁU NA TEMAT BADAŃ
Teoria grafów. Podstawowe pojęcia
W matematyce „wykres” można przedstawić jako obraz przedstawiający liczbę punktów połączonych liniami. „Hrabia” pochodzi od łacińskiego słowa „graphio” – piszę, niczym znany tytuł szlachecki.
W matematyce definicję wykresu podaje się w następujący sposób:
Termin „wykres” w matematyce definiuje się w następujący sposób:
Wykres - jest to skończony zbiór punktów - szczyty, które można połączyć liniami - żeberka .
Przykładami wykresów są rysunki wielokątów, obwodów elektrycznych, schematyczne przedstawienia linii lotniczych, metra, dróg itp. Drzewo genealogiczne to także graf, którego wierzchołkami są członkowie klanu, a więzi rodzinne pełnią rolę krawędzi grafu.
Ryż. 1 Przykłady wykresów
Nazywa się liczbą krawędzi należących do jednego wierzchołka stopień wierzchołka wykresu . Jeśli stopień wierzchołka jest liczbą nieparzystą, wierzchołek nazywa się - dziwne . Jeśli stopień wierzchołka jest liczbą parzystą, wówczas wierzchołek nazywa się nawet.
Ryż. 2 wierzchołek wykresu
Wykres zerowy to graf składający się tylko z izolowanych wierzchołków, które nie są połączone krawędziami.
Kompletny wykres to graf, w którym każda para wierzchołków jest połączona krawędzią. Przykładem kompletnego wykresu może być N-gon, w którym narysowane są wszystkie przekątne.
Jeśli wybierzesz ścieżkę na wykresie, w której pokrywają się punkty początkowe i końcowe, wówczas taka ścieżka zostanie wywołana cykl graficzny . Jeżeli każdy wierzchołek grafu przechodzi przez co najwyżej raz, to cykl zwany prosty .
Jeśli każde dwa wierzchołki grafu są połączone krawędzią, to tak połączony wykres. Wykres nazywa się niepowiązane , jeśli zawiera co najmniej jedną parę niepołączonych wierzchołków.
Jeśli graf jest spójny, ale nie zawiera cykli, to taki graf nazywa się drzewo .
Charakterystyka grafów
Ścieżka hrabiego to sekwencja, w której każde dwie sąsiednie krawędzie mające wspólny wierzchołek występują tylko raz.
Długość najkrótszego łańcucha wierzchołków A i b nazywa się dystans pomiędzy szczytami A i b.
Wierzchołek A zwany centrum wykres, jeśli odległość między wierzchołkami A a każdy inny wierzchołek jest najmniejszym możliwym. Jest taki dystans promień wykres.
Maksymalna możliwa odległość między dowolnymi dwoma wierzchołkami grafu nazywa się średnica wykres.
Kolorowanie i zastosowanie wykresów.
Jeśli przyjrzysz się uważnie mapie geograficznej, zobaczysz linie kolejowe lub autostrady, które są wykresami. Dodatkowo na mapie znajduje się wykres przedstawiający granice pomiędzy krajami (powiatami, regionami).
W 1852 roku student języka angielskiego Francis Guthrie otrzymał zadanie pokolorowania mapy Wielkiej Brytanii, zaznaczając każde hrabstwo innym kolorem. Ze względu na niewielki wybór farb Guthrie użył ich ponownie. Kolorystkę dobrał tak, aby powiaty posiadające wspólny odcinek granicy koniecznie pomalowano na różne kolory. Pojawiło się pytanie jaka jest minimalna ilość farby potrzebna do pokolorowania różnych map. Francis Guthrie zasugerował, choć nie mógł udowodnić, że wystarczą cztery kolory. Problem ten był gorąco dyskutowany w kręgach studenckich, ale później został zapomniany.
„Problem czterech kolorów” budził coraz większe zainteresowanie, lecz nigdy nie został rozwiązany, nawet przez wybitnych matematyków. W 1890 r Angielski matematyk Percy Heawood udowodnił, że wystarczy pięć kolorów, aby pokolorować dowolną mapę. Dopiero w 1968 roku udało im się udowodnić, że do pokolorowania mapy przedstawiającej mniej niż czterdzieści krajów wystarczą 4 kolory.
W 1976 roku problem ten rozwiązali za pomocą komputera dwaj amerykańscy matematycy Kenneth Appel i Wolfgangt Haken. Aby go rozwiązać, wszystkie karty zostały podzielone na 2000 typów. Stworzono program komputerowy, który badał wszystkie typy w celu zidentyfikowania kart, dla których do pokolorowania cztery kolory nie wystarczą. Komputer nie mógł badać tylko trzech rodzajów map, więc matematycy studiowali je samodzielnie. W rezultacie stwierdzono, że do pokolorowania wszystkich 2000 rodzajów kart wystarczą 4 kolory. Ogłosili rozwiązanie problemu czterech kolorów. Tego dnia poczta na uniwersytecie, na którym pracowali Appel i Haken, na wszystkich znaczkach umieściła stempel z napisem: „Wystarczą cztery kolory”.
Trochę inaczej można sobie wyobrazić problem czterech kolorów.
Aby to zrobić, rozważ dowolną mapę, przedstawiając ją w formie wykresu: stolice stanów są wierzchołkami wykresu, a krawędzie wykresu łączą te wierzchołki (kapitały), których stany mają wspólną granicę. Aby otrzymać taki graf, formułuje się następujący problem: należy pokolorować graf czterema kolorami, tak aby wierzchołki posiadające wspólną krawędź zostały pokolorowane różnymi kolorami.
Wykresy Eulera i Hamiltona
W 1859 roku angielski matematyk William Hamilton wypuścił puzzle - drewniany dwunastościan (dwunastościan), którego dwadzieścia wierzchołków oznaczono kołkami. Każdy szczyt miał nazwę jednego z największych miast świata - Kanton, Delhi, Bruksela itp. Zadanie polegało na znalezieniu zamkniętej ścieżki biegnącej wzdłuż krawędzi wielościanu, odwiedzając każdy wierzchołek tylko raz. Do oznaczenia ścieżki używano sznurka, który zawieszano na gwoździach.
Cykl Hamiltona to graf, którego ścieżka jest prostym cyklem przechodzącym jednokrotnie przez wszystkie wierzchołki grafu.
Miasto Kaliningrad (dawniej Królewiec) położone jest nad rzeką Pregel. Rzeka obmywała dwie wyspy, które były połączone ze sobą i z brzegami mostami. Nie ma już starych mostów. Pamięć o nich pozostaje jedynie na mapie miasta.
Któregoś dnia mieszkaniec miasta zapytał przyjaciela, czy można przejść przez wszystkie mosty, odwiedzić każdy tylko raz i wrócić do miejsca, w którym rozpoczął się spacer. Problem ten zainteresował wielu mieszkańców miasta, ale nikt nie mógł go rozwiązać. Zagadnienie to wzbudziło zainteresowanie naukowców z wielu krajów. Rozwiązanie problemu uzyskał matematyk Leonhard Euler. Ponadto sformułował ogólne podejście do rozwiązywania takich problemów. Aby to zrobić, zamienił mapę w wykres. Wierzchołki tego grafu to ląd, a krawędzie to łączące go mosty.
Rozwiązując problem mostu w Królewcu Eulerowi udało się sformułować własności grafów.
Można narysować wykres zaczynając od jednego wierzchołka i kończąc w tym samym wierzchołku jednym pociągnięciem (bez dwukrotnego rysowania tej samej linii i bez odrywania ołówka od papieru), jeśli wszystkie wierzchołki wykresu są równe.
Jeśli istnieje graf z dwoma nieparzystymi wierzchołkami, to jego wierzchołki również można połączyć jednym pociągnięciem. Aby to zrobić, musisz zacząć od jednego i zakończyć na drugim, dowolnym nieparzystym wierzchołku.
Jeżeli istnieje graf mający więcej niż dwa wierzchołki nieparzyste, to nie można go narysować jednym pociągnięciem.
Jeśli zastosujemy te własności do problemu mostów, zobaczymy, że wszystkie wierzchołki badanego grafu są nieparzyste, co oznacza, że tego wykresu nie można połączyć jednym pociągnięciem, tj. Nie da się przejść raz przez wszystkie mosty i zakończyć podróży w miejscu, w którym się zaczęła.
Jeżeli graf ma cykl (niekoniecznie prosty) zawierający jednorazowo wszystkie krawędzie grafu, to taki cykl nazywamy Cykl Eulera . Łańcuch Eulera (ścieżka, cykl, kontur) to łańcuch (ścieżka, cykl, kontur) zawierający jednorazowo wszystkie krawędzie (łuki) grafu.
ROZDZIAŁ II. OPIS BADANIA I JEGO WYNIKÓW
2.1. Etapy badania
Aby przetestować hipotezę, badanie obejmowało trzy etapy (tabela 1):
Etapy badań
Tabela 1.
|
Stosowane metody |
|||
|
Teoretyczne studium problemu |
Studiuj i analizuj literaturę edukacyjną i naukową. |
- samodzielne myślenie; badanie źródeł informacji; - wyszukać niezbędną literaturę. |
|
|
Studium przypadku problemy |
Przeglądaj i analizuj obszary praktyczne zastosowanie wykresy; |
- obserwacja; - analiza; - porównanie; - ankieta. |
|
|
Etap 3. Praktyczne wykorzystanie wyników |
Podsumuj przestudiowane informacje; |
- systematyzacja; raport (ustny, pisemny, z demonstracją materiałów) |
Wrzesień 2017 |
2.2. Obszary praktycznego zastosowania grafów
Wykresy i informacje
Teoria informacji w szerokim zakresie wykorzystuje właściwości drzew binarnych.
Na przykład, jeśli chcesz zakodować określoną liczbę wiadomości w postaci określonych sekwencji zer i jedynek o różnej długości. Kod uważa się za najlepszy dla danego prawdopodobieństwa słów kodowych, jeśli średnia długość słowa jest najmniejsza w porównaniu z innymi rozkładami prawdopodobieństwa. Aby rozwiązać ten problem, Huffman zaproponował algorytm, w którym kod jest reprezentowany w postaci wykresu drzewiastego w ramach teorii wyszukiwania. Dla każdego wierzchołka proponowane jest pytanie, na które odpowiedź może brzmieć „tak” lub „nie” - co odpowiada dwóm krawędziom wychodzącym z wierzchołka. Budowa takiego drzewa zostaje zakończona po ustaleniu, co jest wymagane. Można to wykorzystać podczas przeprowadzania wywiadów z kilkoma osobami, gdy odpowiedź na poprzednie pytanie nie jest z góry znana, plan wywiadu jest reprezentowany w postaci drzewa binarnego.
Wykresy i chemia
A. Cayley rozważał także problem możliwych struktur nasyconych (lub nasyconych) węglowodorów, których cząsteczki określa wzór:
CnH 2n+2
Wszystkie atomy węglowodorów są 4-wartościowe, wszystkie atomy wodoru są 1-wartościowe. Wzory strukturalne Najprostsze węglowodory pokazano na rysunku.
Każdą cząsteczkę nasyconego węglowodoru można przedstawić w postaci drzewa. Kiedy wszystkie atomy wodoru zostaną usunięte, pozostałe atomy węglowodorów utworzą drzewo o wierzchołkach, których stopień nie jest większy niż cztery. Oznacza to, że liczba możliwych pożądanych struktur (homologów danej substancji) jest równa liczbie drzew, których stopień wierzchołkowy nie przekracza 4. Problem ten sprowadza się do problemu wyliczenia drzew danego typu. D. Polya rozważył ten problem i jego uogólnienia.
Wykresy i biologia
Proces rozmnażania bakterii jest jednym z rodzajów procesów rozgałęziających występujących w teorii biologicznej. Niech każda bakteria po pewnym czasie albo umrze, albo podzieli się na dwie części. Zatem dla jednej bakterii otrzymujemy drzewo binarne reprodukcji jej potomstwa. Pytanie problemu jest następujące: ile przypadków zawiera? k potomkowie w n-ta generacja jedna bakteria? Ta zależność w biologii nazywa się procesem Galtona-Watsona i oznacza wymaganą liczbę wymaganych przypadków.
Wykresy i fizyka
Trudnym i żmudnym zadaniem dla każdego radioamatora jest tworzenie obwodów drukowanych (płytki z materiału dielektrycznego - izolującego i wytrawianych ścieżek w postaci metalowych pasków). Przecięcie torów następuje tylko w określonych punktach (lokalizacja triod, rezystorów, diod itp.) według określonych zasad. W rezultacie naukowiec staje przed zadaniem narysowania płaskiego wykresu z wierzchołkami
Wszystko powyższe potwierdza praktyczną wartość wykresów.
Matematyka internetowa
Internet to ogólnoświatowy system połączonych ze sobą sieci komputerowych służących do przechowywania i przesyłania informacji.
Internet można przedstawić w postaci wykresu, którego wierzchołkami są strony internetowe, a krawędziami linki (hiperłącza) prowadzące z jednej witryny do drugiej.
Graf sieciowy (Internet), który ma miliardy wierzchołków i krawędzi, podlega ciągłym zmianom – strony są spontanicznie dodawane i znikane, linki znikają i są dodawane. Jednakże Internet ma strukturę matematyczną, opiera się na teorii grafów i ma kilka „solidnych” właściwości.
Wykres internetowy jest rzadki. Zawiera tylko kilka razy więcej krawędzi niż wierzchołków.
Pomimo swojej rzadkości, Internet jest bardzo zatłoczony. Możesz przejść z jednej strony na drugą za pomocą linków za pomocą 5 - 6 kliknięć (słynna teoria „sześciu uścisków dłoni”).
Jak wiemy, stopień grafu to liczba krawędzi, do których należy dany wierzchołek. Stopnie wierzchołków grafu internetowego rozkładają się zgodnie z pewnym prawem: odsetek witryn (wierzchołków) z dużą liczbą łączy (krawędzi) jest niewielki, a udział witryn z małą liczbą łączy jest duży. Matematycznie można to zapisać w następujący sposób:
gdzie jest proporcją wierzchołków pewnego stopnia, jest stopniem wierzchołka, jest stałą niezależną od liczby wierzchołków w grafie sieciowym, tj. nie zmienia się w trakcie dodawania lub usuwania obiektów (wierzchołków).
To prawo mocy jest uniwersalne dla złożonych sieci - od biologicznych po międzybankowe.
Internet jako całość jest odporny na przypadkowe ataki na strony internetowe.
Ponieważ niszczenie i tworzenie witryn następuje niezależnie i z tym samym prawdopodobieństwem, graf sieciowy z prawdopodobieństwem bliskim 1 zachowuje swoją integralność i nie ulega zniszczeniu.
Aby studiować Internet, konieczne jest zbudowanie losowego modelu wykresu. Model ten powinien mieć właściwości prawdziwego Internetu i nie powinien być zbyt skomplikowany.
Problem ten nie został jeszcze całkowicie rozwiązany! Rozwiązanie tego problemu – zbudowanie wysokiej jakości modelu Internetu – pozwoli nam opracować nowe narzędzia usprawniające wyszukiwanie informacji, identyfikację spamu i rozpowszechnianie informacji.
Budowę modeli biologicznych i ekonomicznych rozpoczęto znacznie wcześniej, niż pojawiło się zadanie zbudowania matematycznego modelu Internetu. Jednak postęp w rozwoju i badaniu Internetu pozwolił odpowiedzieć na wiele pytań dotyczących wszystkich tych modeli.
Matematyka internetowa jest pożądana przez wielu specjalistów: biologów (przewidywanie wzrostu populacji bakterii), finansistów (ryzyko kryzysów) itp. Badanie takich systemów jest jedną z głównych gałęzi matematyki stosowanej i informatyki.
Murmańsk za pomocą wykresu.
Kiedy ktoś przyjeżdża do nowego dla niego miasta, z reguły pierwszym pragnieniem jest zwiedzenie głównych atrakcji. Ale jednocześnie ilość czasu jest często ograniczona, a w przypadku podróży służbowej bardzo mała. Dlatego warto wcześniej zaplanować zwiedzanie. A wykresy będą świetną pomocą w budowaniu trasy!
Jako przykład rozważmy typowy przypadek pierwszego przyjazdu z lotniska do Murmańska. Planujemy odwiedzić następujące atrakcje:
1. Morska Cerkiew Zbawiciela na Wodzie;
2. Katedra św. Mikołaja;
3. Oceanarium;
4. Pomnik kota Siemiona;
5. Lodołamacz nuklearny Lenin;
6. Światła parkowe Murmańska;
7. Parkowa Dolina Komfortu;
8. Most Kolski;
9. Muzeum Historii Murmańskiego Towarzystwa Żeglugowego;
10. Plac Pięciu Kątów;
11. Morski port handlowy
Najpierw zlokalizujmy te miejsca na mapie i uzyskajmy wizualną reprezentację lokalizacji i odległości między atrakcjami. Sieć dróg jest dość rozwinięta, a podróż samochodem nie będzie trudna.
Atrakcje na mapie (po lewej) i powstałym wykresie (po prawej) przedstawia odpowiedni rysunek w ZAŁĄCZNIKU nr 1. W ten sposób przybysz najpierw przejdzie w pobliżu mostu Kola (i, w razie potrzeby, będzie mógł go przekraczać tam i z powrotem); potem zrelaksuje się w Światłach Parku Murmańskiego i Dolinie Komfortu i ruszy dalej. W rezultacie optymalną trasą będzie:
Za pomocą wykresu można także zwizualizować schemat przeprowadzania sondaży. Przykłady przedstawiono w ZAŁĄCZNIKU nr 2. W zależności od udzielonych odpowiedzi respondentowi zadawane są różne pytania. Przykładowo, jeśli w badaniu socjologicznym nr 1 respondent uzna matematykę za najważniejszą z nauk, zostanie zapytany, czy czuje się pewnie na lekcjach fizyki; jeśli uważa inaczej, pytanie drugie będzie dotyczyło popytu humanistyka. Wierzchołki takiego grafu to pytania, a krawędzie to możliwości odpowiedzi.
2.3. Zastosowanie teorii grafów do rozwiązywania problemów
Teorię grafów wykorzystuje się do rozwiązywania problemów z wielu dziedzin: matematyki, biologii, informatyki. Przestudiowaliśmy zasadę rozwiązywania problemów za pomocą teorii grafów i stworzyliśmy własne problemy na temat badań.
Zadanie nr 1.
Pięciu kolegów z klasy uścisnęło sobie dłonie na zjeździe absolwentów szkoły średniej. Ile było uścisków dłoni?
Rozwiązanie: Oznaczmy kolegów z klasy wierzchołkami wykresu. Połączmy każdy wierzchołek liniami z czterema innymi wierzchołkami. Dostajemy 10 linii, to są uściski dłoni.
Odpowiedź: 10 uścisków dłoni (każda linia oznacza jeden uścisk dłoni).
Zadanie nr 2.
We wsi mojej babci, niedaleko jej domu, rośnie 8 drzew: topola, dąb, klon, jabłoń, modrzew, brzoza, jarzębina i sosna. Jarzębina jest wyższa od modrzewia, jabłoń jest wyższa od klonu, dąb jest niższy od brzozy, ale wyższy od sosny, sosna jest wyższa od jarzębiny, brzoza jest niższa od topoli, a modrzew jest wyższy od jabłoni. W jakiej kolejności będą ułożone drzewa od najwyższego do najniższego?
Rozwiązanie:
Drzewa są wierzchołkami grafu. Oznaczmy je pierwszą literą w okręgu. Narysujmy strzałki od niskiego drzewa do wyższego. Mówi się, że jarzębina jest wyższa od modrzewia, następnie umieszczamy strzałę od modrzewia do jarzębiny, brzoza jest niższa od topoli, następnie umieszczamy strzałę od topoli do brzozy itp. Otrzymujemy wykres, na którym widzimy, że najkrótszym drzewem jest klon, następnie jabłoń, modrzew, jarzębina, sosna, dąb, brzoza i topola.
Odpowiedź: klon, jabłko, modrzew, jarzębina, sosna, dąb, brzoza i topola.
Zadanie nr 3.
Mama ma 2 koperty: zwykłą i lotniczą oraz 3 znaczki: kwadratowy, prostokątny i trójkątny. Na ile sposobów mama może wybrać kopertę i znaczek, aby wysłać list do taty?
Odpowiedź: 6 sposobów
Zadanie nr 4.
Między osady Budowane są drogi A, B, C, D, E. Trzeba określić długość najkrótsza ścieżka pomiędzy punktami A i E. Można poruszać się wyłącznie drogami, których długość jest pokazana na rysunku.
Zadanie nr 5.
Trzej koledzy z klasy - Maxim, Kirill i Vova postanowili uprawiać sport i przeszli selekcję sekcji sportowych. Wiadomo, że do sekcji koszykówki zgłosił się 1 chłopiec, a trzech chciało grać w hokeja. Maxim brał udział tylko w przesłuchaniach do sekcji 1, Kirill został wybrany do wszystkich trzech sekcji, a Wowa została wybrana do sekcji 2. Który z chłopców został wybrany do jakiej sekcji sportowej?
Rozwiązanie: Aby rozwiązać problem, skorzystamy z wykresów
Maksym koszykarski
Futbolowy Cyryl
Hokej Wowa
Od do koszykówka idzie tylko jedna strzałka, a następnie Cyryl został wybrany do sekcji koszykówka. Wtedy Cyryl nie zagra hokej, co oznacza w hokej sekcja została wybrana przez Maxima, który przesłuchał tylko do tej sekcji, wtedy będzie Vova piłkarz.
Zadanie nr 6.
W związku z chorobą części nauczycieli dyrektor szkoły jest zobowiązany do sporządzenia fragmentu planu zajęć przynajmniej na jeden dzień, uwzględniając następujące okoliczności:
1. Nauczyciel bezpieczeństwa życia wyraża zgodę na udzielenie jedynie ostatniej lekcji;
2. Nauczyciel geografii może prowadzić drugą lub trzecią lekcję;
3. Matematyk jest gotowy udzielić tylko pierwszej lub tylko drugiej lekcji;
4. Nauczyciel fizyki może prowadzić pierwszą, drugą lub trzecią lekcję, ale tylko w jednej klasie.
Jaki harmonogram może stworzyć dyrektor szkoły, aby zadowolił wszystkich nauczycieli?
Rozwiązanie: Ten problem można rozwiązać, przeglądając wszystko możliwe opcje, ale łatwiej będzie, jeśli narysujesz wykres.
1. 1) fizyka 2. 1) matematyka 3. 1) matematyka
2) matematyka 2) fizyka 2) geografia
3) geografia 3) geografia 3) fizyka
4) OBŻ 4) OBŻ 4) OBŻ
Wniosek
W tej pracy badawczej szczegółowo zbadano teorię grafów, udowodniono hipotezę, że badanie wykresów może pomóc w rozwiązywaniu problemów logicznych, ponadto zbadano teorię grafów w różnych dziedzinach nauki i opracowano 7 problemów.
Wykorzystanie wykresów w nauczaniu uczniów, jak znajdować rozwiązania problemów, pozwala uczniom doskonalić umiejętności graficzne i komunikować rozumowanie w specjalnym języku o skończonym zbiorze punktów, z których część jest połączona liniami. Wszystko to przyczynia się do nauczania uczniów myślenia.
Efektywność działalność edukacyjna w rozwoju myślenia w dużej mierze zależy od stopnia twórczej aktywności uczniów przy rozwiązywaniu problemów matematycznych. W związku z tym istnieje zapotrzebowanie na zadania i ćwiczenia matematyczne aktywizujące aktywność umysłową uczniów.
Stosowanie zadań i wykorzystanie elementów teorii grafów na zajęciach fakultatywnych w szkole precyzyjnie realizuje cel, jakim jest aktywizacja aktywności umysłowej uczniów. Wierzymy, że praktyczny materiał wynikający z naszych badań może przydać się na fakultatywnych zajęciach z matematyki.
Tym samym cel pracy badawczej został osiągnięty, problemy rozwiązane. W przyszłości planujemy kontynuować naukę teorii grafów i opracowywać własne trasy, na przykład wykorzystując wykres do stworzenia trasy wycieczki autobusem szkolnym w ZATO Aleksandrowsk do muzeów i niezapomniane miejsca Murmańsk.
WYKAZ WYKORZYSTANYCH BIBLIOGRAFII
Berezina L. Yu. „Wykresy i ich zastosowanie” - M.: „Oświecenie”, 1979
Gardner M. „Odpoczynek matematyczny”, M. „Mir”, 1972
Gardnera M.” Zagadki matematyczne i rozrywka”, M. „Mir”, 1971
Gorbaczow A. „Zbiór problemów olimpijskich” - M. MTsNMO, 2005
Zykov A. A. Podstawy teorii grafów. - M.: „Księga uniwersytecka”, 2004. - s. 664
Kasatkin V. N. „Niezwykłe problemy matematyki”, Kijów, „Szkoła Radiańska”, 1987
Komponent matematyczny / Redaktorzy i kompilatory N.N. Andreev, S.P. Konovalov, N.M. Panuszkin. - M.: Fundacja „Etiudy Matematyczne” 2015 – 151 s.
Melnikov O. I. „Zabawne problemy w teorii grafów”, Mn. „TetraSystemy”, 2001
Mielnikow O.I. Nie wiem w krainie hrabiów: podręcznik dla studentów. wyd. Po trzecie, stereotypowe. M.: KomKniga, 2007. - 160 s.
Olehnik S. N., Nesterenko Yu. V., Potapov M. K. „Stare zabawne problemy”, M. „Nauka”, 1988
Ruda O. „Wykresy i ich zastosowania”, M. „Mir”, 1965
Harari F. Teoria grafów / Tłumaczenie z języka angielskiego. i przedmowa V. P. Kozyreva. wyd. G. P. Gavrilova. wyd. 2. - M.: Redakcja URSS, 2003. - 296 s.
ZAŁĄCZNIK nr 1
Opracowanie optymalnej trasy zwiedzania głównych atrakcji
Murmańsk za pomocą wykresu.
Optymalną trasą będzie:
8. Most Kolski6. Światła parkowe Murmańska7. Parkowa Dolina Komfortu2. Katedra św. Mikołaja10. Plac Pięciu Kątów5. Lodołamacz nuklearny Lenin9. Muzeum Historii Murmańskiego Towarzystwa Żeglugowego11. Port handlu morskiego1. Morska Cerkiew Zbawiciela na Wodzie4. Pomnik kota Siemiona3. Oceanarium.
PRZEWODNIK PO ATRAKCJACH Murmańska
ZAŁĄCZNIK nr 2
Badania socjologiczne nr 1, 2
Na czym polega metoda grafowa?
Słowo „wykres” w matematyce oznacza obraz przedstawiający kilka narysowanych punktów, z których niektóre są połączone liniami. Przede wszystkim warto powiedzieć, że hrabiowie, o których będziemy dyskutować, nie mają nic wspólnego z arystokratami z dawnych czasów. Nasze „wykresy” wywodzą się z greckiego słowa „grapho”, które oznacza „piszę”. Ten sam rdzeń kryje się w słowach „wykres”, „biografia”.
W matematyce definicja wykresu oblicza się następująco: wykres to skończony zbiór punktów, z których część jest połączona liniami. Punkty nazywane są wierzchołkami grafu, a linie łączące nazywane są krawędziami.
Nazywa się diagram składający się z „izolowanych” wierzchołków wykres zerowy. (ryc. 2)
Grafy, w których nie są zbudowane wszystkie możliwe krawędzie, nazywane są grafami niekompletne wykresy. (ryc. 3)
Grafy, w których zbudowane są wszystkie możliwe krawędzie, nazywane są grafami kompletne wykresy. (ryc. 4)



Graf, w którym każdy wierzchołek jest połączony z krawędzią każdego innego wierzchołka, nazywa się grafem kompletny.
Zauważ, że jeśli pełny graf ma n wierzchołków, to liczba krawędzi będzie równa
n(n-1)/2
Rzeczywiście, liczbę krawędzi w pełnym grafie o n wierzchołkach definiuje się jako liczbę nieuporządkowanych par składających się ze wszystkich n punktów krawędziowych grafu, tj. jako liczbę kombinacji n elementów liczby 2:
Graf, który nie jest kompletny, można uzupełnić o te same wierzchołki, dodając brakujące krawędzie. Na przykład rysunek 3 przedstawia niekompletny graf z pięcioma wierzchołkami. Na rysunku 4 krawędzie przekształcające graf w pełny graf zostały pokazane innym kolorem; zbiór wierzchołków grafu z tymi krawędziami nazywany jest dopełnieniem grafu.
Stopnie wierzchołków i obliczanie liczby krawędzi.
Liczba krawędzi wychodzących z wierzchołka grafu nazywa się stopień wierzchołka. Wierzchołek grafu, który ma stopień nieparzysty nazywamy dziwne, a nawet stopień – nawet.
Jeżeli stopnie wszystkich wierzchołków grafu są równe, wówczas graf nazywa się jednorodny. Zatem każdy pełny graf jest jednorodny.
 Ryc.5
Ryc.5
Rysunek 5 przedstawia graf z pięcioma wierzchołkami. Stopień wierzchołka A będzie oznaczony przez St.A.
Na rysunku: St.A = 1, St.B = 2, St.B = 3, St.G = 2, St.D = 0.
Sformułujmy pewne prawidłowości właściwe niektórym wykresom.
Wzór 1.
Stopnie wierzchołków pełnego grafu są takie same i każdy z nich jest o 1 mniejszy od liczby wierzchołków tego grafu.
Dowód:
Ten wzór jest oczywisty po rozważeniu dowolnego pełnego wykresu. Każdy wierzchołek jest połączony krawędzią z każdym wierzchołkiem oprócz niego samego, tj. z każdego wierzchołka grafu, który ma n wierzchołków, wychodzi n-1 krawędzi, co należało udowodnić.
Wzór 2.
Suma stopni wierzchołków grafu jest liczbą parzystą równą dwukrotności liczby krawędzi grafu.
Ten wzór jest prawdziwy nie tylko dla pełnego wykresu, ale także dla dowolnego wykresu. Dowód:
Rzeczywiście, każda krawędź grafu łączy dwa wierzchołki. Oznacza to, że jeśli dodamy liczbę stopni wszystkich wierzchołków grafu, otrzymamy dwukrotnie większą liczbę krawędzi 2R (R to liczba krawędzi grafu), ponieważ każda krawędź była liczona dwukrotnie, a tego właśnie potrzebowaliśmy udowodnić
Liczba nieparzystych wierzchołków w każdym grafie jest parzysta. Dowód:
Rozważmy dowolny graf G. Niech liczba wierzchołków tego grafu o stopniu 1 będzie równa K1; liczba wierzchołków o stopniu 2 jest równa K2; ...; liczba wierzchołków, których stopień wynosi n, jest równa Kn. Następnie sumę stopni wierzchołków tego grafu można zapisać jako
K1 + 2K2 + ZK3 + ...+ nKn.
Z drugiej strony: jeśli liczba krawędzi grafu wynosi R, to z twierdzenia 2 wiadomo, że suma stopni wszystkich wierzchołków grafu wynosi 2R. Wtedy możemy napisać równość
K1 + 2K2 + ZK3 + ... + nKn = 2R. (1)
Wybierzmy po lewej stronie równości sumę równą liczbie nieparzystych wierzchołków grafu (K1 + K3 + ...):
K1 + 2K2 + ZK3 + 4K4 + 5K5 + ... + nK = 2R,
(K1 + K3 + K5 +...) + (2K2 + 2X3 +4K4 + 4K5 + ...)=2R
Drugi nawias to liczba parzysta będąca sumą liczb parzystych. Wynikowa suma (2R) jest liczbą parzystą. Zatem (K1 + K3 + K5 +...) jest liczbą parzystą.
Rozważmy teraz problemy rozwiązane za pomocą wykresów:
Zadanie. Mistrzostwa klasy . W mistrzostwach klasy tenisa stołowego bierze udział 6 uczestników: Andrey, Boris, Victor, Galina, Dmitry i Elena. Mistrzostwa rozgrywane są w systemie kołowym – każdy uczestnik gra z każdym jeden raz. Do tej pory rozegrano już kilka gier: Andrey grał z Borysem, Galiną i Eleną; Borys, jak już wspomniano, jest z Andriejem, a także z Galiną; Victor - z Galiną, Dmitrijem i Eleną; Galina z Andriejem i Borysem; Dmitry - z Victorem i Eleną - z Andreyem i Victorem. Ile gier rozegrano do tej pory i ile jeszcze pozostało?
Dyskusja. Przedstawmy te zadania w formie diagramu. Przedstawimy uczestników jako kropki: Andriej - punkt A, Borys - punkt B itd. Jeżeli dwóch uczestników grało już ze sobą, wówczas punkty reprezentujące ich połączymy segmentami. Rezultatem jest diagram pokazany na rysunku 1.
Punkty A, B, C, D, D, E są wierzchołkami grafu, a łączące je odcinki krawędziami grafu.
Należy pamiętać, że punkty przecięcia krawędzi grafu nie są jego wierzchołkami.
Liczba rozegranych do tej pory partii jest równa liczbie krawędzi, tj. 7.
Aby uniknąć nieporozumień, wierzchołki wykresu często przedstawia się nie jako kropki, ale jako małe kółka.
Aby znaleźć liczbę gier, które należy rozegrać, zbudujemy kolejny graf z tymi samymi wierzchołkami, ale krawędziami połączymy tych uczestników, którzy jeszcze ze sobą nie grali (ryc. 2). 8 krawędzi, co oznacza, że pozostało do rozegrania 8 partii: Andrey – z Victorem i Dmitrijem; Borys - Z Victorem, Dmitrijem i Eleną itp.
Spróbujmy zbudować wykres dla sytuacji opisanej w następującym zadaniu:
Zadanie . Kto gra Lyapkina - Tyapkina? Szkolne kółko teatralne zdecydowało się wystawić Generalnego Inspektora Gogola. I wtedy wybuchła gorąca dyskusja. Wszystko zaczęło się od Lyapkina - Tyapkina.
Lyapkin - będę Tyapkinem! – stwierdziła stanowczo Gena.
Nie, będę Lyapkinem - Tyapkin sprzeciwił się Dima - Od wczesnego dzieciństwa marzyłem o ożywieniu tego obrazu na scenie.
Cóż, ok, zrezygnuję z tej roli, jeśli pozwolą mi zagrać Chlestakowa” – Gena okazała hojność.
„...A dla mnie - Osipa” – Dima nie ustąpiła mu hojnie.
„Chcę być Truskawką lub Burmistrzem” – powiedziała Wowa.
Nie, ja będę burmistrzem” – krzyczeli jednocześnie Alik i Borya. - Albo Chlestakow, -
Czy uda się tak rozdzielić role, żeby wykonawcy byli usatysfakcjonowani?
Dyskusja.
Przedstawmy młodych aktorów za pomocą kółek w górnym rzędzie: A - Alik, B - Borys, C - Wowa, G - Gena, D - Dima oraz role, które będą odgrywać - za pomocą kółek w drugim rzędzie (1 - Lyapkin - Tyapkin, 2 - Chlestakow, 3 - Osip, 4 - Truskawka, 5 - Burmistrz). Następnie będziemy losować segmenty od każdego uczestnika, tj. żeberka, do ról, które chciałby grać. Otrzymamy graf z dziesięcioma wierzchołkami i dziesięcioma krawędziami (ryc. 3)
Aby rozwiązać problem, musisz wybrać pięć krawędzi z dziesięciu, które nie mają wspólnych wierzchołków. Łatwo to zrobić. Wystarczy zauważyć, że jedna krawędź prowadzi do wierzchołków 3 i 4, odpowiednio z wierzchołków D i B. Oznacza to, że Osip (pierwsza trójka) powinien zagrać Dima (kto jeszcze?), a Zemlyanichkę – Vova. Wierzchołek 1 - Lyapkin - Tyapkin - jest połączony krawędziami z G i D. Krawędź 1 - D poddaje się, ponieważ Dima jest już zajęta, 1 - G pozostaje, Lyapkina - Tyapkina powinna zagrać Gena. Pozostaje połączyć wierzchołki A i B z wierzchołkami 2 i 5, odpowiadającymi rolom Chlestakowa i Gorodnichy. Można to zrobić na dwa sposoby: albo wybrać krawędź A -5 i B - 2, albo krawędź A -2 i B -5. W pierwszym przypadku Alik zagra burmistrza, a Borya – Chlestakowa, w drugim – odwrotnie. Jak pokazuje wykres, problem nie ma innego rozwiązania.
Ten sam wykres otrzymamy rozwiązując następujące zadanie:
Zadanie. Zrzędliwi sąsiedzi. Mieszkańcy pięciu domów pokłócili się między sobą i aby nie spotykać się przy studniach, postanowili je podzielić (studnie), tak aby właściciel każdego domu poszedł do „swojej” studni „swoją” ścieżką. Czy uda im się tego dokonać?
Powstaje pytanie:czy w omawianych problemach rzeczywiście potrzebne były wykresy? Czy nie można znaleźć rozwiązania za pomocą czysto logicznych środków? Tak, możesz. Ale wykresy wyjaśniły warunki, uprościły rozwiązanie i ujawniły podobieństwo problemów, zamieniając dwa problemy w jeden, a to nie jest tak mało. Teraz wyobraźmy sobie problemy, których grafy mają 100 lub więcej wierzchołków. Ale to właśnie takie problemy muszą rozwiązać współcześni inżynierowie i ekonomiści. Nie obejdzie się tutaj bez wykresów.
III. Wykresy Eulera.
Teoria grafów jest nauką stosunkowo młodą: w czasach Newtona takiej nauki jeszcze nie było, choć w użyciu były „drzewa genealogiczne”, czyli odmiany grafów. Pierwsza praca na temat teorii grafów należy do Leonharda Eulera i ukazała się w 1736 roku w publikacjach petersburskiej Akademii Nauk. Pracę tę rozpoczęto od rozważenia następującego problemu:
A) Problem z mostami w Królewcu.
Miasto Królewiec (obecnie Kaliningrad) położone jest na brzegach i dwóch wyspach rzeki Pregel (Pregoli). Poszczególne części miasta zostały połączone siedmioma mostami, jak pokazano na zdjęciu. W niedziele mieszkańcy spacerują po mieście. Czy można wybrać taką trasę, żeby każdy most przejść tylko raz i wrócić do punktu wyjścia?
Zanim rozważymy rozwiązanie tego problemu, wprowadzamy koncepcję „ Wykresy Eulera.
Spróbujmy zakreślić wykres pokazany na ryc. 4 jednym pociągnięciem czyli bez odrywania ołówka od kartki papieru i bez wielokrotnego przechodzenia po tej samej części linii.
Figura ta, tak prosta z wyglądu, okazuje się mieć ciekawą cechę. Jeśli zaczniemy poruszać się od wierzchołka B, to na pewno nam się to uda. Co się stanie, jeśli zaczniemy poruszać się od wierzchołka A? Łatwo zauważyć, że w tym przypadku nie będziemy w stanie prześledzić linii: zawsze będziemy mieli nieprzebyte krawędzie, do których nie będziemy już mogli dotrzeć. 
Na ryc. Rysunek 5 pokazuje wykres, który prawdopodobnie wiesz, jak narysować jednym pociągnięciem. To jest gwiazda. Okazuje się, że choć wygląda na znacznie bardziej skomplikowany niż poprzedni wykres, to można go prześledzić zaczynając od dowolnego wierzchołka.
Wykresy narysowane na ryc. 6 można również narysować jednym pociągnięciem pióra.

Teraz spróbuj narysować jednym pociągnięciem wykres pokazany na ryc. 7
Nie udało Ci się tego zrobić! Dlaczego? Nie możesz znaleźć wierzchołka, którego szukasz? NIE! Nie o to chodzi. Tego wykresu na ogół nie da się narysować jednym pociągnięciem pióra.

Przeprowadźmy rozumowanie, które nas o tym przekona. Rozważmy węzeł A. Wychodzą z niego trzy wierzchołki. Zacznijmy rysować wykres od tego wierzchołka. Aby przejść każdą z tych krawędzi, musimy wyjść z wierzchołka A jedną z nich, w pewnym momencie musimy do niego wrócić drugą i wyjść trzecią. Ale nie będziemy mogli ponownie wejść! Oznacza to, że jeśli zaczniemy rysować od wierzchołka A, nie uda nam się na tym zakończyć.
Załóżmy teraz, że wierzchołek A nie jest początkiem. Następnie w trakcie rysowania musimy wejść do niego jedną z krawędzi, wyjść drugą i wrócić ponownie trzecią. A skoro nie możemy się z tego wydostać, to szczyt A w tym przypadku musi być końcem.
Zatem wierzchołek A musi być węzłem początkowym lub końcowym rysunku.
Ale to samo można powiedzieć o pozostałych trzech wierzchołkach naszego wykresu. Ale wierzchołek początkowy rysunku może być tylko jednym wierzchołkiem, a wierzchołek końcowy również może być tylko jednym wierzchołkiem! Oznacza to, że nie da się narysować tego wykresu jednym pociągnięciem.
Wykres, który można narysować bez odrywania ołówka od papieru, nazywa się Eulera (ryc. 6).
Wykresy te zostały nazwane na cześć naukowca Leonharda Eulera.
Wzór 1. (wynika z twierdzenia, które rozważaliśmy).
Nie można narysować grafu o nieparzystej liczbie nieparzystych wierzchołków.
Wzór 2.
Jeśli wszystkie wierzchołki wykresu są równe, możesz narysować ten wykres nie odrywając ołówka od papieru („jednym pociągnięciem”), przesuwając się wzdłuż każdej krawędzi tylko raz. Ruch może rozpocząć się od dowolnego wierzchołka i zakończyć w tym samym wierzchołku.
Wzór 3.
Wykres zawierający tylko dwa nieparzyste wierzchołki można narysować bez odrywania ołówka od papieru, a ruch musi rozpocząć się w jednym z tych nieparzystych wierzchołków i zakończyć się na drugim z nich.
Wzór 4.
Grafu mającego więcej niż dwa wierzchołki nieparzyste nie można narysować „jednym pociągnięciem”.
Figurę (wykres), którą można narysować bez odrywania ołówka od papieru, nazywa się jednokierunkową.
Wykres nazywa się zgodny, jeśli dowolne dwa jego wierzchołki można połączyć ścieżką, to znaczy ciągiem krawędzi, z których każda zaczyna się na końcu poprzedniej.
Wykres nazywa się niespójny, jeśli ten warunek nie jest spełniony.
 Ryc.7
Ryc.7  Ryc.8
Ryc.8
Rysunek 7 wyraźnie pokazuje rozłączony wykres. Jeśli na rysunku narysujesz krawędź pomiędzy wierzchołkami D i E, graf stanie się spójny. (ryc. 8)
W teorii grafów taka krawędź (po usunięciu której graf zmienia się z połączonego na rozłączony) nazywa się most.
Przykładami mostów na rysunku 7 mogą być krawędzie DE, A3, VZh itp., z których każda łączyłaby wierzchołki „izolowanych” części grafu (rys. 8).
Rozłączony wykres składa się z kilku „części”. Te „kawałki” nazywane są elementy łączności wykres. Każdy połączony komponent jest oczywiście spójnym grafem. Należy pamiętać, że spójny wykres ma jeden spójny komponent.
TWIERDZENIE.
Graf jest eulerowski wtedy i tylko wtedy, gdy jest spójny i ma co najwyżej dwa nieparzyste wierzchołki.
Dowód:
Rysując wykres dla każdego wierzchołka, z wyjątkiem wierzchołka początkowego i końcowego, wejdziemy tyle samo razy, ile z niego wyjdziemy. Dlatego stopnie wszystkich wierzchołków muszą być parzyste, z wyjątkiem dwóch, co oznacza, że graf Eulera ma co najwyżej dwa nieparzyste wierzchołki.
Wróćmy teraz do problemu mostów królewieckich.
Omówienie problemu . Oznaczmy różne części miasta literami A, B, C, D, a mosty literami a, b, c, d, e, f, g - mosty łączące odpowiednie części miasta. W tym problemie są tylko przejścia przez mosty: przechodząc przez dowolny most, zawsze trafiamy z jednej części miasta do drugiej i odwrotnie, przechodząc z jednej części miasta do drugiej, z pewnością przejdziemy przez most. Przedstawmy zatem plan miasta w postaci wykresu, którego wierzchołki A, B, C, D (ryc. 8) przedstawiają poszczególne części miasta, a krawędzie a, b, c, d, e , f, g to mosty łączące odpowiednie części miasta. Często wygodniej jest przedstawiać krawędzie nie jako odcinki proste, ale jako krzywoliniowe - „łuki”.
Gdyby istniała trasa spełniająca warunki zadania, wówczas występowałoby zamknięte, ciągłe przechodzenie przez ten graf, przebiegające raz wzdłuż każdej krawędzi. Inaczej mówiąc, wykres ten należy narysować jednym pociągnięciem. Jest to jednak niemożliwe – niezależnie od tego, który wierzchołek wybierzemy jako początkowy, będziemy musieli przejść przez pozostałe wierzchołki, a jednocześnie przez każdą „dochodzącą” krawędź (most, którym weszliśmy do tej części miasta) będzie odpowiadać „wychodzącej” krawędzi, mostowi, po którym będziemy następnie korzystać z tej części miasta): liczba krawędzi wchodzących do każdego wierzchołka będzie równa liczbie krawędzi wychodzących z niego, tj. całkowita liczba krawędzie zbiegające się w każdym wierzchołku muszą być równe. Nasz wykres nie spełnia tego warunku i dlatego wymagana trasa nie istnieje.
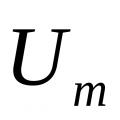 Parametry elektryczne i czasowe impulsów prostokątnych
Parametry elektryczne i czasowe impulsów prostokątnych Grawitopłat – wynalazek czy fikcja B
Grawitopłat – wynalazek czy fikcja B Prezentacja „Czasowników frazowych”, na którą czekamy
Prezentacja „Czasowników frazowych”, na którą czekamy