Gjennomgangsspørsmål for kapittel 8. Gjennomgangsspørsmål for kapittel VI.
Ferdige lekser til geometrilærebok for elever på 7-9 trinn, forfattere: L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev, E.G. Poznyak, I.I. Yudina, Prosveshchenie forlag for studieåret 2015-2016.
Gutter, i klasse 7-9 vil du studere et så interessant emne som geometri. For å unngå å ha problemer med å forstå denne leksjonen i fremtiden, må du jobbe hardt helt fra begynnelsen.
I tidligere klasser har du allerede blitt kjent med noen geometriske former. I denne buzzen vil du utvide dette minimum av kunnskap. Hele kurset er delt inn i to deler: planimetri og stereometri. I klasse 7 og 8 skal du se på figurer på et plan - dette er et avsnitt om planimetri. I 9. klasse, egenskaper til figurer i rommet - stereometri.
Ofte oppstår det en situasjon når det ut fra forholdene ikke er mulig å lage riktig tegning, tegne alle detaljene i rommet, og da virker geometri som et umulig fag for deg. Hvis du begynner å få slike vanskeligheter, anbefaler vi å bruke vår geometritest for klasse 7-9 L.S. Atanasyan, som er lagt ut nedenfor.
GDZ Geometry grade 7 arbeidsbok Atanasyan kan lastes ned.
GDZ Geometry grade 8 arbeidsbok Atanasyan kan lastes ned.
GDZ Geometry klasse 9 arbeidsbok Atanasyan kan lastes ned.
GDZ for didaktisk materiale om geometri for grad 7 Ziv B.G. kan lastes ned.
GDZ for didaktisk materiale om geometri for grad 8 Ziv B.G. kan lastes ned.
GDZ for didaktisk materiale om geometri for grad 9 Ziv B.G. kan lastes ned.
GDZ for selvstendig og testarbeid i geometri for klasse 7-9 Ichenskaya M.A. kan lastes ned.
GDZ for innsamling av geometrioppgaver for klasse 7 Ershova A.P. kan lastes ned.
GDZ for innsamling av geometrioppgaver for klasse 8 Ershova A.P. kan lastes ned.
GDZ for en arbeidsbok om geometri for klasse 9 Mishchenko T.M. kan lastes ned.
GDZ for tematiske tester i geometri for klasse 7 Mishchenko T.M. kan lastes ned.
GDZ for tematiske tester i geometri for klasse 8 Mishchenko T.M. kan lastes ned
1. Hvor mange linjer kan trekkes gjennom to punkter?
2. Hvor mange felles punkter kan to rette linjer ha?
3. Forklar hva et segment er.
4. Forklar hva en bjelke er. Hvordan betegnes strålene?
5. Hvilken figur kalles en vinkel? Forklar hva toppunktet og sidene av en vinkel er.
6. Hvilken vinkel kalles utviklet?
7. Hvilke figurer kalles like?
8. Forklar hvordan man sammenligner to linjestykker.
9. Hvilket punkt kalles midtpunktet i segmentet?
10. Forklar hvordan man sammenligner to vinkler.
11. Hvilken stråle kalles halveringslinjen til en vinkel?
12. Punkt C deler segment AB i to segmenter. Hvordan finne lengden på segment AB hvis lengdene på segmentene AC og CB er kjent?
13. Hvilke verktøy brukes for å måle avstander?
14. Hva er gradmålet for en vinkel?
15. Ray OS deler vinkel AOB i to vinkler. Hvordan finne gradmålet for vinkel AOB hvis gradmålene for vinklene AOC og COB er kjent?
16. Hvilken vinkel kalles spiss? rett? dum?
17. Hvilke vinkler kalles tilstøtende? Hva er summen av tilstøtende vinkler?
18. Hvilke vinkler kalles vertikale? Hvilke egenskaper har vertikale vinkler?
19. Hvilke linjer kalles perpendikulære?
20. Forklar hvorfor to linjer vinkelrett på den tredje ikke skjærer hverandre.
21. Hvilke enheter brukes for å konstruere rette vinkler på bakken?
Tilleggsoppgaver for kapittel I
71. Merk fire punkter slik at ingen tre ligger på samme rette linje. Tegn en rett linje gjennom hvert par punkter. Hvor mange rette linjer fikk du?
72. Gitt fire linjer, som hver to krysser hverandre. Hvor mange skjæringspunkter har disse linjene hvis bare to linjer går gjennom hvert skjæringspunkt?
73. Hvor mange uutviklede vinkler dannes når tre linjer som går gjennom ett punkt, krysser hverandre?
74. Punkt N ligger på segmentet MP. Avstanden mellom punktene M og P er 24 cm, og avstanden mellom punktene N og M er to ganger avstanden mellom punktene N og P. Finn avstanden:
a) mellom punktene N og P;
b) mellom punktene N og M.
75. Tre punkter K, L, M ligger på samme rette linje, KL = 6 cm, LM = 10 cm Hva kan avstanden KM være? For hvert av de mulige tilfellene, lag en tegning.
76. Et segment AB med lengde a er delt med punktene P og Q i tre segmenter AP, PQ og QB slik at AP - 2PQ = 2QB. Finn avstanden mellom:
a) punkt A og midten av segmentet QB;
b) midtpunktene til segmentene AP og QB.
77. Et segment med lengde m er delt:
a) i tre like deler;
b) i fem like deler.
Finn avstanden mellom midten av de ekstreme delene.
78. Et segment på 36 cm er delt inn i fire ulike deler. Avstanden mellom sentrene til de ytterste delene er 30 cm Finn avstanden mellom sentrene til midtdelene.
79. Punktene A, B og C ligger på samme linje, punktene M og N er midtpunktene til segmentene AB og AC. Bevis at BC = 2MN.
80. Det er kjent at ZAOB = 35°, ZBOC = 50°. Finn vinkel AOC. For hvert mulig tilfelle, lag en tegning med en linjal og gradskive.
81. Vinkel hk er lik 120°, og vinkel hm er lik 150°. Finn vinkelen km. For hvert av de mulige tilfellene, lag en tegning.
82. Finn tilstøtende vinkler hvis:
a) en av dem er 45° større enn den andre;
b) deres forskjell er 35°.
83. Finn vinkelen som dannes av halveringslinjene til to tilstøtende vinkler.
84. Bevis at halveringslinjene til vertikale vinkler ligger på samme rette linje.
85. Bevis at hvis halveringslinjene til vinklene ABC og CBD er vinkelrette, så ligger punktene A, B og D på samme rette linje.
86. Gitt to kryssende linjer a og b og et punkt A som ikke ligger på disse linjene. Linjene m og n trekkes gjennom punkt A slik at m⊥a, n⊥b. Bevis at linjene m og n ikke er like.
1 Gi eksempler på vektormengder kjent for deg fra fysikkkurset ditt.
2 Definer en vektor. Forklar hvilken vektor som kalles null.
3 Hva er lengden på en vektor som ikke er null? Hva er lengden på nullvektoren?
4 Hvilke vektorer kalles kollineære? Tegn co-directional vektorer og og motsatt rettede vektorer i figuren.
5 Definer like vektorer.
6 Forklar betydningen av uttrykket: "Vektoren er forsinket fra punkt A." Bevis at du fra ethvert punkt kan plotte en vektor lik den gitte, og bare en.
7 Forklar hva vektoren kalles summen av to vektorer. Hva er trekantregelen for å legge til to vektorer?
8 Bevis at for enhver vektor likheten
9 Formuler og bevis et teorem om lovene for vektoraddisjon.
10 Hva er parallellogramregelen for å addere to ikke-kollineære vektorer?
11 Hva er polygonregelen for å legge til flere vektorer?
12 Hvilken vektor kalles forskjellen mellom to vektorer? Konstruer forskjellen mellom to gitte vektorer.
13 Hvilken vektor kalles motsatt av denne? Formuler og bevis vektorforskjellsteoremet.
14 Hvilken vektor kalles produktet av en gitt vektor og et gitt tall?
15 Hva er produktet lik
16 Kan vektorer være ikke-kollineære?
17 Formuler de grunnleggende egenskapene ved å multiplisere en vektor med et tall.
18 Gi et eksempel på bruk av vektorer for å løse geometriske problemer.
19 Hvilket segment kalles midtlinjen til trapesen?
20 Angi og bevis teoremet om midtlinjen til en trapes.
Tilleggsoppgaver for kapittel IX
800. Bevis at hvis vektorene er co-directional, så og hvis de er motsatt rettet, og da
801. Bevis at ulikhetene er gyldige for alle vektorer
802. På siden BC av trekant ABC er punktet N markert slik at BN = 2NC. Uttrykk vektor i form av vektorer
803. På sidene MN og NP i trekanten MNP er punktene X og Y markert henholdsvis slik at ![]()
804. Basen AD til trapesen ABCD er tre ganger større enn basen BC. På siden AD er et punkt K markert slik at ![]() Uttrykk vektorer i form av vektorer
Uttrykk vektorer i form av vektorer
805. Tre punkter A, B og C er plassert slik at Bevis at for ethvert punkt O er likheten sann ![]()
806. Punkt C deler segmentet AB i forholdet m: n, tellende fra punkt A. Bevis at for ethvert punkt O er likheten sann
1. Forklar hvordan arealene til polygoner måles.
2. Formuler de grunnleggende egenskapene til arealene til polygoner.
3. Hvilke polygoner kalles like store og hvilke kalles like-sammenhengende?
4. Formuler og bevis et teorem om å beregne arealet til et rektangel.
5. Formuler og bevis et teorem om å beregne arealet til et parallellogram.
6. Formuler og bevis et teorem om å beregne arealet til en trekant. Hvordan beregne arealet av en rettvinklet trekant fra bena?
7. Formuler og bevis et teorem om forholdet mellom arealene til to trekanter som har like vinkler.
8. Formuler og bevis et teorem om å beregne arealet til en trapes.
9. Formuler og bevis Pythagoras teorem.
10. Formuler og bevis teoremet omvendt til Pythagoras teorem.
11. Hvilke trekanter kalles Pythagoras? Gi eksempler på pytagoreiske trekanter.
12. Hvilken formel for arealet av en trekant kalles Herons formel? Utled denne formelen.
Tilleggsoppgaver
500. Bevis at arealet av en firkant konstruert på siden av en likebenet rettvinklet trekant er to ganger arealet av en firkant konstruert i høyden tegnet til hypotenusen.
501. Arealet til tomten er 27 hektar. Uttrykk arealet til samme tomt: a) i kvadratmeter; b) i kvadratkilometer.
502. Høyden på parallellogrammet er 5 cm og 4 cm, og omkretsen er 42 cm. Finn arealet av parallellogrammet.
503. Finn omkretsen til et parallellogram hvis arealet er 24 cm 2 og skjæringspunktet mellom diagonalene er 2 cm og 3 cm unna sidene.
504. Den minste siden av parallellogrammet er 29 cm. En perpendikulær trukket fra skjæringspunktet mellom diagonalene til den større siden deler den inn i segmenter lik 33 cm og 12 cm. Finn arealet av parallellogrammet.
505. Bevis at av alle trekantene der den ene siden er lik a og den andre er lik b, har den med sidene vinkelrett størst areal.
506. Hvordan tegne to rette linjer gjennom toppunktet til en firkant for å dele den inn i tre figurer med like store arealer?
507.* Hver side av den ene trekanten er større enn hvilken som helst side av den andre trekanten. Følger det av dette at arealet av den første trekanten er større enn arealet til den andre trekanten?
508.* Bevis at summen av avstandene fra et punkt på bunnen av en likebenet trekant til sidesidene ikke avhenger av posisjonen til dette punktet.
509. Bevis at summen av avstandene fra et punkt som ligger innenfor en likesidet trekant til sidene ikke avhenger av posisjonen til dette punktet.
510.* Gjennom punkt D, som ligger på siden BC av trekant ABC, trekkes linjer parallelt med de to andre sidene og kryssende sider AB og AC, henholdsvis i punktene E og F. Bevis at trekantene CDE og BDF er like store.
511. I en trapesformet ABCD med sidene AB og CD, skjærer diagonalene seg i punkt O.
a) Sammenlign arealene til trekantene ABD og ACD.
b) Sammenlign arealene til trekantene ABO og CDO.
c) Bevis at likheten OA OB = OS OD holder.
512.* Basene til en trapes er lik a og b. Et segment med ender på sidene av trapeset, parallelt med basene, deler trapeset i to like trapeser. Finn lengden på dette segmentet.
513. Diagonalene til en rombe er 18 m og 24 m. Finn omkretsen til romben og avstanden mellom parallelle sider.
514. Arealet til en rombe er 540 cm 2, og en av diagonalene er 4,5 dm. Finn avstanden fra skjæringspunktet mellom diagonalene til siden av romben.
515. Finn arealet av en likebenet trekant hvis: a) siden er 20 cm og vinkelen ved bunnen er 30°; b) høyden tegnet til siden er 6 cm og danner en vinkel på 45° med basen.
516. I trekant ABC, BC = 34 cm. Den vinkelrette MN trukket fra midten av BC til den rette linjen AC deler siden AC i segmenter AN = 25 cm og NC = 15 cm. Finn arealet av trekanten ABC.
517. Finn arealet av firkant ABCD, der AB = 5 cm, BC = 13 cm, CD = 9 cm, DA = 15 cm, AC = 12 cm.
518. Finn arealet av en likebenet trapes hvis: a) dens mindre base er 18 cm, høyden er 9 cm og dens spisse vinkel er 45°; b) dens baser er 16 cm og 30 cm, og diagonalene er innbyrdes vinkelrette.
519. Finn arealet til en likebenet trapes hvis høyde er lik h og hvis diagonaler er innbyrdes perpendikulære.
520. Diagonalene til en likebenet trapes er innbyrdes perpendikulære, og summen av basene er 2a. Finn arealet av trapesen.
521. Bevis at hvis diagonalene til firkanten ABCD er vinkelrett på hverandre, så er AD 2 + BC 2 = AB 2 + CD 2.
522. I en likebenet trapes ABCD med base AD = 17 cm, BC = 5 cm og side AB = 10 cm, trekkes en rett linje gjennom toppunkt B, som halverer diagonal AC og krysser grunnflate AD ved punkt M. Finn arealet av trekant BDM.
523. To ruter med side a har ett felles toppunkt, og siden til den ene ligger på diagonalen til den andre. Finn arealet til den vanlige delen av disse rutene.
524. Sidene i trekanten er 13 cm, 5 cm og 12 cm. Finn arealet av denne trekanten.
525. Avstanden fra punkt M, som ligger innenfor trekanten ABC, til linje AB er 6 cm, og til linje AC er 2 cm. Finn avstanden fra punkt M til linje BC, hvis AB = 13 cm, BC = 14 cm, AC = 15 cm.
526. I en rombe er høyden lik cm 2/3 av den større diagonalen. Finn området til romben.
527. I en likebenet trapes er diagonalen 10 cm og høyden 6 cm Finn arealet av trapesen.
528. I trapes ABCD skjærer diagonalene i punkt O. Finn arealet av trekanten AOB hvis sidesiden CD av trapesen er 12 cm, og avstanden fra punkt O til den rette linjen CD er 5 cm.
529. Diagonalene til en firkant er 16 cm og 20 cm og skjærer hverandre i en vinkel på 30°. Finn arealet til denne firkanten.
530. I en likebenet trekant ABC med grunnflaten BC er høyden AD 8 cm. Finn arealet av trekanten ABC hvis medianen DM av trekanten ADC er 8 cm.
531. Sidene AB og BC i rektangel ABCD er lik henholdsvis 6 cm og 8 cm. En linje som går gjennom toppunktet C og vinkelrett på linjen BD skjærer side AD i punkt M, og diagonal BD ved punkt K. Finn arealet av firkant ABKM.
532. I trekant ABC er høyden BH tegnet. Bevis at hvis:
a) vinkel A er spiss, da BC 2 = AB 2 + AC 2 - 2AC AN;
b) vinkel A er stump, da er BC 2 = AB 2 + AC 2 + 2AC AN.
Svar på problemer
1. Hva kalles forholdet mellom to segmenter?
2. I hvilket tilfelle sies de at segmentene AB og CD er proporsjonale med segmentene A 1 B 1 og C 1 D 1?
3. Definer lignende trekanter.
4. Formuler og bevis et teorem om forholdet mellom arealene til like trekanter.
5. Formuler og bevis et teorem som uttrykker det første tegnet på likhet til trekanter.
6. Formuler og bevis et teorem som uttrykker det andre kriteriet for likhet i trekanter.
7. Formuler og bevis et teorem som uttrykker det tredje kriteriet for likhet i trekanter.
8. Hvilket segment kalles trekantens midtlinje? Angi og bevis teoremet om midtlinjen til en trekant.
9. Bevis at medianene til en trekant skjærer hverandre i ett punkt, som deler hver median i forholdet 2:1, regnet fra toppunktet.
10. Formuler og bevis påstanden om at høyden til en rettvinklet trekant trukket fra toppen av en rett vinkel deler trekanten i like trekanter.
11. Angi og bevis påstander om proporsjonale segmenter i en rettvinklet trekant.
12. Gi et eksempel på å løse et konstruksjonsproblem ved hjelp av likhetsmetoden.
13. Fortell oss hvordan du bestemmer høyden til et objekt på bakken og avstanden til et utilgjengelig punkt.
14. Forklar hvilke to figurer som kalles like. Hva er likhetskoeffisienten til figurer?
15. Hva kalles sinus, cosinus, tangens til en spiss vinkel i en rettvinklet trekant?
16. Bevis at hvis en spiss vinkel i en rettvinklet trekant er lik en spiss vinkel i en annen rettvinklet trekant, så er sinusene til disse vinklene like, cosinusene til disse vinklene er like og tangentene til disse vinklene er like.
17. Hvilken likhet kalles den grunnleggende trigonometriske identiteten?
18. Hva er verdiene av sinus, cosinus og tangens for vinkler på 30°, 45°, 60°? Begrunn svaret ditt.
Tilleggsoppgaver
604. Trekanter ABC og A 1 B 1 C 1 er like, AB = 6 cm, BC - 9 cm, C A = 10 cm. Den største siden av trekanten A 1 B 1 C 1 er 7,5 cm Finn de to andre sidene av trekant A 1 B 1 C 1 .
605. Diagonal AC til trapeset ABCD deler den i to like trekanter. Bevis at AC 2 = a b, hvor a og b er basene til trapesen.
606. Halvlederne MD og NK i trekanten MNP skjærer hverandre i punkt O. Finn relasjonen OK: PÅ hvis MN = 5 cm, NP = 3 cm, MP = 7 cm.
607. Grunnlaget til en likebenet trekant er relatert til siden som 4: 3, og høyden trukket til grunnflaten er 30 cm. Finn segmentene som halveringslinjen til vinkelen ved grunnflaten deler denne høyden i.
608. På fortsettelsen av sidesiden OB av den likebenede trekanten AO B med grunnflaten AB, tas punktet C slik at punktet B ligger mellom punktene O og C. Segment AC skjærer halveringslinjen til vinkelen AOB i punktet M. Bevis at AM< МС.
609. Punkt D er tatt på siden BC av trekant ABC slik at Bevis at AD er halveringslinjen til trekant ABC.
610. En rett linje parallelt med siden AB i trekanten ABC deler siden AC i forholdet 2:7, regnet fra toppunktet A. Finn sidene til den kuttede trekanten hvis AB = 10 cm, BC = 18 cm, CA = 21,6 cm.
611. Bevis at medianen AM av trekanten ABC halverer ethvert segment parallelt med siden BC hvis ender ligger på sidene AB og AC.
612. To stolper AB og CD av ulik lengde a og b er installert vertikalt i en viss avstand fra hverandre som vist i figur 210. Endene A og D, B og C er forbundet med tau som skjærer hverandre i punkt O. Basert på data i figuren, beviser at Hva:
Finn x og bevis at x ikke er avhengig av avstanden d mellom polene AB og CD.

Ris. 210
613. Bevis at trekantene ABC og A 1 B 1 C 1 er like hvis:
EN) ![]() , hvor VM og B 1 M 1 er medianene til trekantene;
, hvor VM og B 1 M 1 er medianene til trekantene;
b) ∠A = ∠A 1, ![]() , hvor ВН og В 1 Н 1 er høydene til trekantene АВС og A 1 B 1 C 1.
, hvor ВН og В 1 Н 1 er høydene til trekantene АВС og A 1 B 1 C 1.
614. Diagonalene til en rektangulær trapes ABCD med rett vinkel A er innbyrdes perpendikulære. Basen AB er 6 cm og siden AD er 4 cm Finn DC, DB og CB.
615.* Et segment med ender på sidene av en trapes er parallell med basene og går gjennom skjæringspunktet mellom diagonalene. Finn lengden på dette segmentet hvis basene til trapeset er lik a og b.
616. Bevis at toppunktene i en trekant er like langt fra linjen som inneholder midtlinjen.
617. Bevis at midtpunktene på sidene til en rombe er toppunktene til et rektangel.
618. Punktene M og N er henholdsvis midtpunktene på sidene CD og BC på parallellogrammet ABCD. Bevis at linjene AM og AN deler diagonalen BD i tre like deler.
619. Halveringslinjen til den ytre vinkelen ved toppunktet A til trekant ABC skjærer linjen BC i punkt D. Bevis at .
620. I trekant ABC (AB≠ AC) trekkes en linje gjennom midten av siden BC, parallelt med halveringslinjen til vinkel A, som skjærer linjene AB og AC, henholdsvis i punktene D og E. Bevis at BD = CE .
621. I en trapes ABCD med basene AD og BC er summen av basene b, diagonalen AC er a, ∠ACB = α. Finn arealet av trapesen.
622. Punkt K er markert på side AD av parallellogram ABCD slik at AK = 1/4 KD. Diagonal AC og segment B K skjærer hverandre i punktet P. Finn arealet av parallellogram ABCD hvis arealet av trekanten ARK er 1 cm 2.
623. I en rektangulær trapes ABCD med base AD og BC ∠A = ∠B = 90°, ∠ACD = 90°, BC = 4 cm, AD = 16 cm Finn vinklene C og D på trapesen.
624. Bevis at medianene til en trekant deler den inn i seks trekanter hvis arealer er parvis like.
625. Basen AD til en likebenet trapes ABCD er 5 ganger større enn basen BC. Høyden BH skjærer diagonalen AC i punkt M, arealet av trekanten AMN er 4 cm 2. Finn arealet av trapes ABCD.
626. Bevis at trekanter ABC og A 1 B 1 C 1 er like hvis ![]() der AD og A 1 D 1 er halveringslinjene til trekantene.
der AD og A 1 D 1 er halveringslinjene til trekantene.
Byggeoppgaver
627. Gitt en trekant ABC. Konstruer en trekant A1B1C1, lik trekant ABC, hvis areal er to ganger arealet av trekanten ABC.
628. Gitt tre segmenter, hvis lengder er henholdsvis lik a, b og c. Konstruer et segment hvis lengde er lik .
629. Konstruer en trekant hvis midtpunktene til sidene er gitt.
630. Konstruer en trekant ved å bruke en side og medianer trukket til de to andre sidene.
 Mikhail Lermontov-diktet "Motherland" (Jeg elsker fedrelandet mitt, men med en merkelig kjærlighet!
Mikhail Lermontov-diktet "Motherland" (Jeg elsker fedrelandet mitt, men med en merkelig kjærlighet!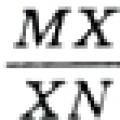 Gjennomgangsspørsmål for kapittel VI
Gjennomgangsspørsmål for kapittel VI Emner: Naturressurser i Fjernøsten Beskyttelse av vannressurser i landet og regionen vår
Emner: Naturressurser i Fjernøsten Beskyttelse av vannressurser i landet og regionen vår