Normalfordeling og dens parametere. Normal lov om sannsynlighetsfordeling Hvilke parametere karakteriserer normalfordelingen
I mange problemer knyttet til normalfordelte tilfeldige variabler er det nødvendig å bestemme sannsynligheten for at en tilfeldig variabel , underlagt en normallov med parametere, faller på segmentet fra til . For å beregne denne sannsynligheten bruker vi den generelle formelen
hvor er fordelingsfunksjonen til mengden .
La oss finne fordelingsfunksjonen til en tilfeldig variabel fordelt etter en normallov med parametere. Fordelingstettheten til verdien er lik:
Herfra finner vi fordelingsfunksjonen
 . (6.3.3)
. (6.3.3)
La oss gjøre en endring av variabel i integralet (6.3.3)
og la oss sette det i denne formen:
 (6.3.4)
(6.3.4)
Integral (6.3.4) uttrykkes ikke gjennom elementære funksjoner, men det kan beregnes gjennom en spesiell funksjon som uttrykker bestemt integral fra uttrykket eller (det såkalte sannsynlighetsintegralet) som tabellene er kompilert for. Det er mange varianter av slike funksjoner, for eksempel:
 ;
;

etc. Hvilken av disse funksjonene som skal brukes er en smakssak. Vi vil velge en slik funksjon
 . (6.3.5)
. (6.3.5)
Det er lett å se at denne funksjonen ikke er noe annet enn en fordelingsfunksjon for en normalfordelt tilfeldig variabel med parametere.
La oss bli enige om å kalle funksjonen en normalfordelingsfunksjon. Vedlegget (tabell 1) inneholder tabeller over funksjonsverdier.
La oss uttrykke fordelingsfunksjonen (6.3.3) til mengden med parametere og gjennom normalfordelingsfunksjonen. Åpenbart,
La oss nå finne sannsynligheten for at en tilfeldig variabel faller på seksjonen fra til . I henhold til formel (6.3.1)
Dermed uttrykte vi sannsynligheten for at en tilfeldig variabel fordelt i henhold til en normallov med eventuelle parametere kommer inn i en seksjon gjennom standardfordelingsfunksjonen som tilsvarer den enkleste normalloven med parametere 0.1. Legg merke til at argumentene til funksjonen i formel (6.3.7) har en veldig enkel betydning: det er avstanden fra høyre ende av seksjonen til spredningssenteret, uttrykt i standardavvik; - samme avstand for venstre ende av seksjonen, og denne avstanden anses som positiv hvis enden er plassert til høyre for spredningssenteret, og negativ hvis til venstre.
Som enhver distribusjonsfunksjon har funksjonen følgende egenskaper:
3. - ikke-minkende funksjon.
I tillegg, fra symmetrien til normalfordelingen med parametere i forhold til opprinnelsen, følger det at
Ved å bruke denne egenskapen ville det strengt tatt vært mulig å begrense funksjonstabellene til kun positive argumentverdier, men for å unngå en unødvendig operasjon (subtraksjon fra en), gir vedleggstabell 1 verdier for både positive og negative argumenter.

I praksis møter vi ofte problemet med å beregne sannsynligheten for at en normalfordelt stokastisk variabel faller inn i et område som er symmetrisk med hensyn til spredningssenteret. La oss vurdere en slik lengdedel (fig. 6.3.1). La oss beregne sannsynligheten for å treffe dette området ved å bruke formel (6.3.7):
Ved å ta hensyn til egenskapen (6.3.8) til funksjonen og gi venstre side av formel (6.3.9) en mer kompakt form, får vi en formel for sannsynligheten for at en tilfeldig variabel fordelt i henhold til normalloven faller inn i en område symmetrisk med hensyn til spredningssenteret:
![]() .
(6.3.10)
.
(6.3.10)
La oss løse følgende problem. La oss plotte etterfølgende lengdesegmenter fra spredningssenteret (fig. 6.3.2) og beregne sannsynligheten for at en tilfeldig variabel faller inn i hver av dem. Siden normalkurven er symmetrisk, er det nok å plotte slike segmenter bare i én retning.

Ved å bruke formel (6.3.7) finner vi:
 (6.3.11)
(6.3.11)
Som man kan se fra disse dataene, er sannsynlighetene for å treffe hvert av de følgende segmentene (femte, sjette, etc.) med en nøyaktighet på 0,001 lik null.
Ved å avrunde sannsynlighetene for å komme inn i segmenter til 0,01 (til 1%), får vi tre tall som er enkle å huske:
0,34; 0,14; 0,02.
Summen av disse tre verdiene er 0,5. Dette betyr at for en normalfordelt stokastisk variabel passer all spredning (med en nøyaktighet på brøkdeler av en prosent) innenfor området .
Dette gjør det mulig, med kjennskap til standardavviket og den matematiske forventningen til en tilfeldig variabel, å grovt angi rekkevidden av dens praktisk mulige verdier. Denne metoden for å estimere rekkevidden av mulige verdier for en tilfeldig variabel er kjent i matematisk statistikk kalt "tre sigma-regelen". Regelen om tre sigma innebærer også en omtrentlig metode for å bestemme standardavviket til en tilfeldig variabel: ta det maksimale praktisk mulige avviket fra gjennomsnittet og del det på tre. Selvfølgelig kan denne grove teknikken bare anbefales hvis det ikke finnes andre, mer nøyaktige metoder for å bestemme.
Eksempel 1. En tilfeldig variabel fordelt etter en normallov representerer en feil ved måling av en viss avstand. Ved måling tillates en systematisk feil i retning av overestimering med 1,2 (m); Standardavviket for målefeilen er 0,8 (m). Finn sannsynligheten for at avviket til den målte verdien fra den sanne verdien ikke vil overstige 1,6 (m) i absolutt verdi.
Løsning. Målefeilen er en tilfeldig variabel underlagt normalloven med parametere og . Vi må finne sannsynligheten for at denne mengden faller på seksjonen fra til . I henhold til formel (6.3.7) har vi:
Ved å bruke funksjonstabellene (vedlegg, tabell 1), finner vi:
![]() ;
,
;
,
Eksempel 2. Finn samme sannsynlighet som i forrige eksempel, men forutsatt at det ikke er noen systematisk feil.
Løsning. Ved å bruke formel (6.3.10), forutsatt , finner vi:
Eksempel 3. Et mål som ser ut som en stripe (motorvei), hvis bredde er 20 m, skytes i retning vinkelrett på motorveien. Sikting utføres langs senterlinjen på motorveien. Standardavviket i skyteretningen er lik m. Det er en systematisk feil i skyteretningen: underskuddet er 3 m. Finn sannsynligheten for å treffe en motorvei med ett skudd.
Den mest kjente og hyppigst brukte loven i sannsynlighetsteori er normalfordelingsloven eller Gauss lov .
hovedfunksjon normalfordelingsloven er at den er det ytterste lov for andre distribusjonslover.
Merk at for en normalfordeling har integralfunksjonen formen:
 .
.
La oss nå vise at den sannsynlige betydningen av parameterne er som følger: EN er den matematiske forventningen, - standardavviket (dvs.) for normalfordelingen:
a) per definisjon av den matematiske forventningen til en kontinuerlig tilfeldig variabel, har vi

Egentlig
 ,
,
siden under integrertegnet er det merkelig funksjon, og grensene for integrasjon er symmetriske om opprinnelsen;
 - Poisson-integral .
- Poisson-integral .
Så den matematiske forventningen til en normalfordeling er lik parameteren EN .
b) per definisjon av variansen til en kontinuerlig tilfeldig variabel og, med tanke på at , kan vi skrive
 .
.
Integrering av deler, putting  , la oss finne
, la oss finne

Derfor ![]() .
.
Så standardavviket til normalfordelingen er lik parameteren.
 |
I tilfelle og normal distribusjon kalt normalisert (eller standard normal) fordeling. Da vil åpenbart den normaliserte tettheten (differensial) og den normaliserte integralfordelingsfunksjonen skrives henholdsvis i formen:

(Funksjonen kalles som kjent Laplace-funksjonen (se FOREDRAG 5) eller sannsynlighetsintegralet. Begge funksjonene, dvs. ![]() , tabellert og deres verdier er registrert i de tilsvarende tabellene).
, tabellert og deres verdier er registrert i de tilsvarende tabellene).
Egenskaper for normalfordeling (egenskapene til normalkurven):
1. Tydeligvis en funksjon på hele tallinjen.
2. ![]() , det vil si at normalkurven er plassert over aksen Åh
.
, det vil si at normalkurven er plassert over aksen Åh
.
3. ![]() , altså aksen Åh
fungerer som den horisontale asymptoten til grafen.
, altså aksen Åh
fungerer som den horisontale asymptoten til grafen.
4. En normalkurve er symmetrisk om en rett linje x = a (følgelig er grafen til funksjonen symmetrisk om aksen OU ).
Derfor kan vi skrive: .
5.  .
.
6. Det er lett å vise at poengene  Og
Og  er bøyningspunkter for normalkurven (bevis det selv).
er bøyningspunkter for normalkurven (bevis det selv).
7.Det er åpenbart det

men siden  , Det
, Det ![]() . I tillegg
. I tillegg ![]() , derfor er alle odde øyeblikk lik null.
, derfor er alle odde øyeblikk lik null.
For selv øyeblikk kan vi skrive:

8.  .
.
9.  .
.
10. ![]() , Hvor .
, Hvor .
11. For negative verdier av den tilfeldige variabelen: , hvor .
13. Sannsynligheten for at en tilfeldig variabel faller inn i en seksjon som er symmetrisk i forhold til sentrum av fordelingen er lik:

EKSEMPEL 3. Vis at en normalfordelt tilfeldig variabel X avviker fra matematisk forventning M(X) ikke mer enn .
Løsning. For normalfordeling: ![]() .
.

Med andre ord, sannsynligheten for at den absolutte verdien av avviket vil overstige trippel er standardavviket svært lite, nemlig lik 0,0027. Dette betyr at kun i 0,27 % av tilfellene kan dette skje. Slike hendelser, basert på prinsippet om umuligheten av usannsynlige hendelser, kan anses som praktisk talt umulige.
Så en hendelse med en sannsynlighet på 0,9973 kan betraktes som praktisk talt pålitelig, det vil si at den tilfeldige variabelen avviker fra den matematiske forventningen med ikke mer enn .
EKSEMPEL 4. Kjenne til egenskapene til normalfordelingen til en tilfeldig variabel X - Strekkfasthet av stål: kg/mm2 og kg/mm2, finn sannsynligheten for å oppnå stål med en strekkfasthet fra 31 kg/mm2 til 35 kg/mm2.
Løsning.
3. Eksponentialfordeling (eksponentiell distribusjonslov)
 |
Eksponentiell er sannsynlighetsfordelingen til en kontinuerlig tilfeldig variabel. X , som er beskrevet av en differensialfunksjon (fordelingstetthet)

hvor er en konstant positiv verdi.
Eksponentialfordelingen er definert en parameter. Denne funksjonen til den eksponentielle fordelingen indikerer fordelen sammenlignet med distribusjoner som er avhengige av et større antall parametere. Vanligvis er parametrene ukjente og deres estimater (omtrentlig verdi) må finnes; Selvfølgelig er det lettere å evaluere én parameter enn to, eller tre osv.
 |
Det er lett å skrive den integrerte:

Vi definerte eksponentialfordelingen ved hjelp av en differensialfunksjon; det er klart at det kan bestemmes ved hjelp av integralfunksjonen.
Kommentar: Tenk på en kontinuerlig tilfeldig variabel T
- hvor lenge produktet ikke fungerer som den skal. Dens aksepterte verdier er merket med t
, . Kumulativ distribusjons funksjon ![]() definerer sannsynlighet for feil produkter over en periode t
. Følgelig er sannsynligheten for feilfri drift i løpet av samme tid, varighet t
, det vil si at sannsynligheten for den motsatte hendelsen er lik
definerer sannsynlighet for feil produkter over en periode t
. Følgelig er sannsynligheten for feilfri drift i løpet av samme tid, varighet t
, det vil si at sannsynligheten for den motsatte hendelsen er lik
Normal distribusjon ( normal distribusjon) - spiller en viktig rolle i dataanalyse.
Noen ganger i stedet for begrepet normal fordeling bruke begrepet Gaussisk fordeling til ære for K. Gauss (eldre betegnelser som praktisk talt ikke brukes i dag: Gauss’ lov, Gauss-Laplace-fordeling).
Univariat normalfordeling
En normalfordeling har en tetthet::
I denne formelen er de faste parametrene gjennomsnitt, - standard avvik.
Tetthetsgrafer for ulike parametere er gitt.
Den karakteristiske funksjonen til normalfordelingen har formen:
![]()
Differensiere den karakteristiske funksjonen og innstillingen t = 0, får vi øyeblikk av hvilken som helst rekkefølge.
Normalfordelingstetthetskurven er symmetrisk med hensyn til og har et enkelt maksimum på dette punktet, lik
Standardavviksparameteren varierer fra 0 til ∞.
Gjennomsnitt varierer fra -∞ til +∞.
Når parameteren øker, sprer kurven seg langs aksen X, når den nærmer seg 0, krymper den rundt gjennomsnittsverdien (parameteren karakteriserer spredningen, spredningen).
Når det endres kurven forskyves langs aksen X(se grafer).
Ved å variere parametrene og får vi ulike modeller tilfeldige variabler, som oppstår i telefoni.
En typisk anvendelse av normalloven i analyse av for eksempel telekommunikasjonsdata er modellering av signaler, beskrivelse av støy, interferens, feil og trafikk.
Univariate normalfordelingsplott

Figur 1. Tetthetsplott for normalfordeling: gjennomsnitt er 0, standardavvik er 1

Figur 2. Tetthetsplott av standard normalfordeling med regioner som inneholder 68 % og 95 % av alle observasjoner

Figur 3. Tetthetsgrafer av normalfordelinger med null gjennomsnitt og ulike avvik (=0,5, =1, =2)

Figur 4 Grafer over to normalfordelinger N(-2,2) og N(3,2).
Legg merke til at midten av distribusjonen har forskjøvet seg når du endrer parameteren.
Kommentar
I et program STATISTIKA Betegnelsen N(3,2) refererer til normal- eller gaussisk lov med parametrene: gjennomsnitt = 3 og standardavvik =2.
I litteraturen tolkes noen ganger den andre parameteren som spredning, dvs. torget standardavvik.
Beregne normalfordeling i prosentpoeng ved hjelp av en sannsynlighetskalkulator STATISTIKA
Bruke en sannsynlighetskalkulator STATISTIKA Du kan beregne ulike egenskaper ved distribusjoner uten å ty til de tungvinte tabellene som brukes i gamle bøker.
Trinn 1. La oss lansere Analyse / Sannsynlighetskalkulator / Distribusjoner.
I distribusjonsdelen velger du normal.

Figur 5. Lansering avoren
Steg 2. Vi angir parameterne som interesserer oss.
For eksempel ønsker vi å beregne 95 %-kvantilen av en normalfordeling med et gjennomsnitt på 0 og et standardavvik på 1.
La oss indikere disse parameterne i feltene til kalkulatoren (se kalkulatorfeltene gjennomsnitt og standardavvik).
La oss legge inn parameteren p=0,95.
Avmerkingsboks "Reverse f.r." vises automatisk. Merk av for "Tidsplan".
Klikk på "Beregn"-knappen i øvre høyre hjørne.

Figur 6. Innstilling av parametere
Trinn 3. I Z-feltet får vi resultatet: kvantilverdien er 1,64 (se neste vindu).

Figur 7. Vise resultatet av kalkulatoren

Figur 8. Tetthetsplott og distribusjonsfunksjoner. Rett linje x=1,644485




Figur 9. Grafer over normalfordelingsfunksjonen. Vertikale stiplede linjer - x=-1,5, x=-1, x=-0,5, x=0


Figur 10. Grafer over normalfordelingsfunksjonen. Vertikale stiplede linjer - x=0,5, x=1, x=1,5, x=2
Estimering av normalfordelingsparametere
Normalfordelingsverdier kan beregnes ved hjelp av interaktiv kalkulator.
Bivariat normalfordeling
Den endimensjonale normalfordelingen generaliserer naturlig til todimensjonal normal distribusjon.
For eksempel, hvis du vurderer et signal på bare ett punkt, er en endimensjonal fordeling nok for deg, på to punkter - todimensjonalt, på tre punkter - tredimensjonalt, etc.
Den generelle formelen for den bivariate normalfordelingen er:

Hvor er den parvise korrelasjonen mellom X 1 Og X 2;
X 1 henholdsvis;
Gjennomsnitt og standardavvik for en variabel X 2 hhv.
Hvis tilfeldige variabler X 1 Og X 2 er uavhengige, da er korrelasjonen henholdsvis 0, = 0, mellomleddet i eksponenten forsvinner, og vi har:
f(x 1,x 2) = f(x 1)*f(x 2)
For uavhengige mengder dekomponerer den todimensjonale tettheten til produktet av to endimensjonale tettheter.
Tetthetsplott av bivariate normalfordelinger

Figur 11. Tetthetsplott av en bivariat normalfordeling (nullvektor av gjennomsnitt, enhetskovariansmatrise)

Figur 12. Utsnitt av tetthetsgrafen for en todimensjonal normalfordeling med et plan z=0,05

Figur 13. Tetthetsplott av en todimensjonal normalfordeling (nullvektor av forventet verdi, kovariansmatrise med 1 på hoveddiagonalen og 0,5 på sidediagonalen)

Figur 14. Utsnitt av tetthetsgrafen til en todimensjonal normalfordeling (nullvektor for matematisk forventning, kovariansmatrise med 1 på hoveddiagonalen og 0,5 på sidediagonalen) etter plan z= 0,05

Figur 15. Tetthetsplott av en todimensjonal normalfordeling (nullvektor av forventet verdi, kovariansmatrise med 1 på hoveddiagonalen og -0,5 på sidediagonalen)

Figur 16. Utsnitt av tetthetsgrafen til en todimensjonal normalfordeling (nullvektor for matematisk forventning, kovariansmatrise med 1 på hoveddiagonalen og -0,5 på sidediagonalen) etter plan z=0,05

Figur 17. Utsnitt av tetthetsgrafer av en todimensjonal normalfordeling med et plan z=0,05
For bedre å forstå den bivariate normalfordelingen, prøv å løse følgende problem.
Oppgave. Se på grafen for den bivariate normalfordelingen. Tenk på det, kan det representeres som en rotasjon av grafen til en endimensjonal normalfordeling? Når bør du bruke deformasjonsteknikken?
I praksis påvirkes de fleste tilfeldige variabler av et stort nummer av tilfeldige faktorer er underlagt den normale sannsynlighetsfordelingsloven. Derfor, i ulike anvendelser av sannsynlighetsteori, er denne loven av spesiell betydning.
Den tilfeldige variabelen $X$ følger den normale sannsynlighetsfordelingsloven hvis dens sannsynlighetsfordelingstetthet har følgende form
$$f\left(x\right)=((1)\over (\sigma \sqrt(2\pi )))e^(-(((\left(x-a\right))^2)\over ( 2(\sigma )^2)))$$
Grafen til funksjonen $f\left(x\right)$ er vist skjematisk i figuren og kalles "Gaussisk kurve". Til høyre for denne grafen er den tyske 10 mark-seddelen, som ble brukt før innføringen av euroen. Hvis du ser nøye etter, kan du på denne seddelen se Gauss-kurven og dens oppdager, den største matematikeren Carl Friedrich Gauss.
La oss gå tilbake til vår tetthetsfunksjon $f\left(x\right)$ og gi noen forklaringer angående distribusjonsparameterne $a,\ (\sigma )^2$. Parameteren $a$ karakteriserer spredningssenteret for verdiene til en tilfeldig variabel, det vil si at den har betydningen av en matematisk forventning. Når parameteren $a$ endres og parameteren $(\sigma )^2$ forblir uendret, kan vi observere et skifte i grafen til funksjonen $f\left(x\right)$ langs abscissen, mens tetthetsgrafen selv endrer ikke form.

Parameteren $(\sigma )^2$ er variansen og karakteriserer formen på tetthetsgrafkurven $f\left(x\right)$. Når du endrer parameteren $(\sigma )^2$ med parameteren $a$ uendret, kan vi observere hvordan tetthetsgrafen endrer form, komprimerer eller strekker seg, uten å bevege seg langs abscisseaksen.

Sannsynlighet for at en normalfordelt stokastisk variabel faller inn i et gitt intervall
Som kjent kan sannsynligheten for at en tilfeldig variabel $X$ faller inn i intervallet $\left(\alpha ;\ \beta \right)$ beregnes $P\left(\alpha< X < \beta \right)=\int^{\beta }_{\alpha }{f\left(x\right)dx}$. Для нормального распределения случайной величины $X$ с параметрами $a,\ \sigma $ справедлива следующая формула:
$$P\venstre(\alpha< X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right)$$
Her er funksjonen $\Phi \left(x\right)=((1)\over (\sqrt(2\pi )))\int^x_0(e^(-t^2/2)dt)$ Laplace funksjon . Verdiene til denne funksjonen er hentet fra . Følgende egenskaper for funksjonen $\Phi \left(x\right)$ kan noteres.

1 . $\Phi \left(-x\right)=-\Phi \left(x\right)$, det vil si at funksjonen $\Phi \left(x\right)$ er merkelig.
2 . $\Phi \left(x\right)$ er en monotont økende funksjon.
3 . $(\mathop(lim)_(x\to +\infty ) \Phi \left(x\right)\ )=0,5$, $(\mathop(lim)_(x\to -\infty ) \ Phi \ venstre(x\høyre)\ )=-0,5$.
For å beregne verdiene til funksjonen $\Phi \left(x\right)$, kan du også bruke funksjonen $f_x$-veiviseren i Excel: $\Phi \left(x\right)=NORMDIST\left(x) ;0;1;1\høyre )-0,5$. La oss for eksempel beregne verdiene til funksjonen $\Phi \left(x\right)$ for $x=2$.

Sannsynligheten for at en normalfordelt tilfeldig variabel $X\in N\left(a;\ (\sigma )^2\right)$ faller inn i et intervallsymmetrisk med hensyn til den matematiske forventningen $a$ kan beregnes ved hjelp av formelen
$$P\venstre(\venstre|X-a\høyre|< \delta \right)=2\Phi \left({{\delta }\over {\sigma }}\right).$$
Tre sigma regel. Det er nesten sikkert at en normalfordelt tilfeldig variabel $X$ vil falle inn i intervallet $\left(a-3\sigma ;a+3\sigma \right)$.
Eksempel 1 . Den tilfeldige variabelen $X$ er underlagt den normale sannsynlighetsfordelingsloven med parametere $a=2,\ \sigma =3$. Finn sannsynligheten for at $X$ faller inn i intervallet $\left(0.5;1\right)$ og sannsynligheten for å tilfredsstille ulikheten $\left|X-a\right|< 0,2$.
Ved hjelp av formel
$$P\venstre(\alpha< X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right),$$
vi finner $P\left(0.5;1\right)=\Phi \left(((1-2)\over (3))\right)-\Phi \left(((0.5-2)\ over (3) ))\right)=\Phi \left(-0.33\right)-\Phi \left(-0.5\right)=\Phi \left(0.5\right)-\Phi \ left(0.33\right)=0.191- 0,129=$0,062.
$$P\venstre(\venstre|X-a\høyre|< 0,2\right)=2\Phi \left({{\delta }\over {\sigma }}\right)=2\Phi \left({{0,2}\over {3}}\right)=2\Phi \left(0,07\right)=2\cdot 0,028=0,056.$$
Eksempel 2 . Anta at i løpet av året er prisen på aksjer i et bestemt selskap en tilfeldig variabel fordelt i henhold til normalloven med en matematisk forventning lik 50 konvensjonelle pengeenheter og et standardavvik lik 10. Hva er sannsynligheten for at på en tilfeldig valgt dagen i perioden under diskusjon vil prisen for kampanjen være:
a) mer enn 70 konvensjonelle pengeenheter?
b) under 50 per aksje?
c) mellom 45 og 58 konvensjonelle pengeenheter per aksje?
La den tilfeldige variabelen $X$ være prisen på aksjer i et selskap. Etter betingelse er $X$ underlagt en normalfordeling med parametere $a=50$ - matematisk forventning, $\sigma =10$ - standardavvik. Sannsynlighet $P\venstre(\alpha< X < \beta \right)$ попадания $X$ в интервал $\left(\alpha ,\ \beta \right)$ будем находить по формуле:
$$P\venstre(\alpha< X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right).$$
$$а)\ P\left(X>70\right)=\Phi \left(((\infty -50)\over (10))\right)-\Phi \left(((70-50)\ over (10))\right)=0,5-\Phi \left(2\right)=0,5-0,4772=0,0228.$$
$$b)\P\venstre(X< 50\right)=\Phi \left({{50-50}\over {10}}\right)-\Phi \left({{-\infty -50}\over {10}}\right)=\Phi \left(0\right)+0,5=0+0,5=0,5.$$
$$in)\ P\venstre(45< X < 58\right)=\Phi \left({{58-50}\over {10}}\right)-\Phi \left({{45-50}\over {10}}\right)=\Phi \left(0,8\right)-\Phi \left(-0,5\right)=\Phi \left(0,8\right)+\Phi \left(0,5\right)=$$
Normal sannsynlighetsfordelingslov
Uten overdrivelse kan det kalles en filosofisk lov. Når vi observerer ulike objekter og prosesser i verden rundt oss, kommer vi ofte over det faktum at noe ikke er nok, og at det er en norm: 
Her er et grunnleggende syn tetthetsfunksjoner normal sannsynlighetsfordeling, og jeg ønsker deg velkommen til denne interessante leksjonen.
Hvilke eksempler kan du gi? Det er rett og slett mørke av dem. Dette er for eksempel høyden, vekten til mennesker (og ikke bare), deres fysiske styrke, mentale evner osv. Det er en "hovedmesse" (av en eller annen grunn) og det er avvik i begge retninger.
Dette er forskjellige egenskaper ved livløse gjenstander (samme størrelse, vekt). Dette er en tilfeldig varighet av prosesser, for eksempel tidspunktet for et hundre meter løp eller transformasjonen av harpiks til rav. Fra fysikk husket jeg luftmolekyler: noen av dem er langsomme, noen er raske, men de fleste beveger seg med "standard" hastigheter.
Deretter avviker vi fra midten med ett standardavvik til og beregner høyden: 
Markeringspunkter på tegningen (grønn farge) og vi ser at dette er nok.
På sluttstadiet tegner vi forsiktig en graf, og spesielt nøye reflektere det konveks/konkav! Vel, du har sikkert skjønt for lenge siden at x-aksen er horisontal asymptote, og det er absolutt forbudt å "klatre" bak den!
Når du arkiverer en løsning elektronisk, er det enkelt å lage en graf i Excel, og uventet for meg selv tok jeg til og med inn en kort video om dette emnet. Men først, la oss snakke om hvordan formen på normalkurven endres avhengig av verdiene til og.
Når du øker eller reduserer "a" (med konstant "sigma") grafen beholder sin form og beveger seg til høyre/venstre hhv. Så for eksempel når funksjonen tar formen ![]() og grafen vår "flytter" 3 enheter til venstre - nøyaktig til opprinnelsen til koordinatene:
og grafen vår "flytter" 3 enheter til venstre - nøyaktig til opprinnelsen til koordinatene: 
En normalfordelt mengde med null matematisk forventning fikk et helt naturlig navn - sentrert; dens tetthetsfunksjon er til og med, og grafen er symmetrisk om ordinaten.
Ved endring av "sigma" (med konstant "a"), grafen "forblir den samme", men endrer form. Når den forstørres, blir den lavere og langstrakt, som en blekksprut som strekker tentaklene. Og omvendt, når du reduserer grafen blir smalere og høyere- det viser seg å være en "overrasket blekksprut". Ja når avta"sigma" to ganger: den forrige grafen smalner og strekker seg opp to ganger: 
Alt er i full overensstemmelse med geometriske transformasjoner av grafer.
En normalfordeling med en enhetssigmaverdi kalles normalisert, og hvis det også er det sentrert(vårt tilfelle), så kalles en slik fordeling standard. Den har enda mer enkel funksjon tetthet, som allerede er påtruffet i Laplaces lokale teorem: ![]() . Standarddistribusjonen har fått bred anvendelse i praksis, og snart vil vi endelig forstå formålet.
. Standarddistribusjonen har fått bred anvendelse i praksis, og snart vil vi endelig forstå formålet.
Vel, la oss nå se filmen:
Ja, helt rett – liksom ufortjent holdt det seg i skyggen sannsynlighetsfordelingsfunksjon. La oss huske henne definisjon:
- sannsynligheten for at en tilfeldig variabel vil ta en verdi MINDRE enn variabelen som "løper gjennom" alle reelle verdier til "pluss" uendelig.
Inne i integralet brukes vanligvis en annen bokstav slik at det ikke er noen "overlapping" med notasjonen, for her er hver verdi assosiert med feil integral, som er lik noen Antall fra intervallet.
Nesten alle verdier kan ikke beregnes nøyaktig, men som vi nettopp har sett, med moderne datakraft er dette ikke vanskelig. For standarddistribusjonsfunksjonen inneholder den tilsvarende Excel-funksjonen generelt ett argument:
=NORMSDIST(z)
En, to - og du er ferdig: 
Tegningen viser tydelig gjennomføringen av alle fordelingsfunksjonsegenskaper, og fra de tekniske nyansene her bør du ta hensyn til horisontale asymptoter og bøyningspunktet.
La oss nå huske en av hovedoppgavene til emnet, nemlig finne ut hvordan du finner sannsynligheten for at en normal tilfeldig variabel vil ta verdien fra intervallet. Geometrisk er denne sannsynligheten lik område mellom normalkurven og x-aksen i den tilsvarende delen: 
men hver gang jeg prøver å få en omtrentlig verdi  er urimelig, og derfor er det mer rasjonelt å bruke "enkel" formel:
er urimelig, og derfor er det mer rasjonelt å bruke "enkel" formel:
.
! Husker også , Hva
Her kan du bruke Excel igjen, men det er et par viktige "men": for det første er det ikke alltid tilgjengelig, og for det andre vil "ferdige" verdier mest sannsynlig reise spørsmål fra læreren. Hvorfor?
Jeg har snakket om dette mange ganger før: en gang (og for ikke så lenge siden) var en vanlig kalkulator en luksus, og i pedagogisk litteratur Den "manuelle" metoden for å løse problemet under vurdering er fortsatt bevart. Dens essens er å standardisere verdiene "alfa" og "beta", det vil si redusere løsningen til standardfordelingen: ![]()
Merk
: funksjonen er lett å få tak i fra den generelle saken ved hjelp av lineær erstatninger. Så også:
ved hjelp av lineær erstatninger. Så også:
og fra utskiftingen som er utført, følger formelen for overgangen fra verdiene til en vilkårlig distribusjon til de tilsvarende verdiene for standardfordelingen.
Hvorfor er dette nødvendig? Faktum er at verdiene ble omhyggelig beregnet av våre forfedre og satt sammen i en spesiell tabell, som er i mange bøker om terwer. Men enda oftere er det en verditabell, som vi allerede har behandlet i Laplaces integralteorem:
Hvis vi har til rådighet en verditabell for Laplace-funksjonen  , så løser vi gjennom det:
, så løser vi gjennom det:
Brøkverdier er tradisjonelt avrundet til 4 desimaler, slik det gjøres i standardtabellen. Og for kontroll er det Punkt 5 oppsett.
Jeg minner deg om det, og for å unngå forvirring alltid kontroll, en tabell over HVILKEN funksjon er foran øynene dine.
Svar kreves oppgitt i prosent, så den beregnede sannsynligheten må multipliseres med 100 og resultatet gis med en meningsfull kommentar:
– med en flytur fra 5 til 70 m vil omtrent 15,87 % av skjellene falle
Vi trener på egenhånd:
Eksempel 3
Diameteren på fabrikklagde lagre er en tilfeldig variabel, normalfordelt med en matematisk forventning på 1,5 cm og et standardavvik på 0,04 cm Finn sannsynligheten for at størrelsen på et tilfeldig valgt lager varierer fra 1,4 til 1,6 cm.
I prøveløsningen og nedenfor vil jeg bruke Laplace-funksjonen som det vanligste alternativet. Merk forresten at etter ordlyden kan endene av intervallet tas med i vurderingen her. Dette er imidlertid ikke kritisk.
Og allerede i dette eksemplet møtte vi et spesielt tilfelle - når intervallet er symmetrisk i forhold til den matematiske forventningen. I en slik situasjon kan den skrives i form og ved å bruke merkeligheten til Laplace-funksjonen forenkle arbeidsformelen:

Delta-parameteren kalles avvik fra den matematiske forventningen, og den doble ulikheten kan "pakkes" vha modul:
– sannsynligheten for at verdien av en tilfeldig variabel vil avvike fra den matematiske forventningen med mindre enn .
Det er bra at løsningen passer på én linje :)
– sannsynligheten for at diameteren til et tilfeldig tatt lager ikke avviker fra 1,5 cm med mer enn 0,1 cm.
Resultatet av denne oppgaven viste seg å være nær enhet, men jeg vil ha enda større pålitelighet - nemlig å finne ut grensene som diameteren ligger innenfor nesten alle lagre. Er det noe kriterium for dette? Finnes! Spørsmålet som stilles besvares av den såkalte
tre sigma regel
Dens essens er det praktisk talt pålitelig
er det faktum at en normalfordelt tilfeldig variabel vil ta en verdi fra intervallet ![]() .
.
Sannsynligheten for avvik fra forventet verdi er faktisk mindre enn:
eller 99,73 %
Når det gjelder lager, er dette 9973 stykker med en diameter fra 1,38 til 1,62 cm og bare 27 "substandard" kopier.
I praktisk forskning Tre sigma-regelen brukes vanligvis i motsatt retning: if statistisk sett Det ble funnet at nesten alle verdier tilfeldig variabel som studeres faller innenfor et intervall på 6 standardavvik, så er det tungtveiende grunner til å tro at denne verdien er fordelt etter en normallov. Verifikasjon utføres ved hjelp av teori statistiske hypoteser.
Vi fortsetter å løse de harde sovjetiske problemene:
Eksempel 4
Den tilfeldige verdien av veiefeilen er fordelt etter normalloven med null matematisk forventning og et standardavvik på 3 gram. Finn sannsynligheten for at neste veiing vil bli utført med en feil som ikke overstiger 5 gram i absolutt verdi.
Løsning veldig enkelt. Etter betingelse merker vi umiddelbart at ved neste veiing (noe eller noen) vi vil nesten 100% få resultatet med en nøyaktighet på 9 gram. Men problemet innebærer et smalere avvik og i henhold til formelen:
![]() – sannsynligheten for at neste veiing vil bli utført med en feil som ikke overstiger 5 gram.
– sannsynligheten for at neste veiing vil bli utført med en feil som ikke overstiger 5 gram.
Svar:
Det løste problemet er fundamentalt forskjellig fra et tilsynelatende likt. Eksempel 3 leksjon om uniform distribusjon. det var en feil avrunding måleresultater, her snakker vi om den tilfeldige feilen til selve målingene. Slike feil oppstår på grunn av de tekniske egenskapene til selve enheten. (utvalget av akseptable feil er vanligvis angitt i passet hans), og også på grunn av eksperimentørens feil - når vi for eksempel "med øyet" tar avlesninger fra nålen på samme skalaer.
Blant annet er det også såkalte systematisk målefeil. Det er allerede ikke tilfeldig feil som oppstår på grunn av feil oppsett eller bruk av enheten. For eksempel kan uregulerte gulvvekter stadig "legge til" kilo, og selgeren veier systematisk ned kundene. Eller det kan beregnes ikke systematisk. Imidlertid vil en slik feil i alle fall ikke være tilfeldig, og forventningen er forskjellig fra null.
…jeg utvikler et salgsopplæringskurs for øyeblikket =)
La oss løse det omvendte problemet selv:
Eksempel 5
Diameteren på valsen er en tilfeldig normalfordelt tilfeldig variabel, standardavviket er lik mm. Finn lengden på intervallet, symmetrisk i forhold til den matematiske forventningen, som lengden på rullediameteren sannsynligvis faller inn i.
Punkt 5* design layoutå hjelpe. Vær oppmerksom på at den matematiske forventningen ikke er kjent her, men dette hindrer oss ikke i det minste fra å løse problemet.
OG eksamensoppgave, som jeg anbefaler for å konsolidere materialet:
Eksempel 6
En normalfordelt tilfeldig variabel spesifiseres av dens parametere (matematisk forventning) og (standardavvik). Påkrevd:
a) skriv ned sannsynlighetstettheten og skildre skjematisk grafen;
b) finn sannsynligheten for at den vil ta en verdi fra intervallet ![]() ;
;
c) finn sannsynligheten for at den absolutte verdien vil avvike fra ikke mer enn ;
d) ved å bruke "tre sigma"-regelen, finn verdiene til den tilfeldige variabelen.
Slike problemer tilbys overalt, og i løpet av årene med praksis har jeg løst hundrevis og hundrevis av dem. Sørg for å trene på å tegne en tegning for hånd og bruke papirtabeller;)
Vel, jeg skal se på et eksempel på økt kompleksitet:
Eksempel 7
Stil en tilfeldig variabel har formen ![]() . Finn, matematisk forventning, varians, distribusjonsfunksjon, bygge tetthetsgrafer og distribusjonsfunksjoner, finn.
. Finn, matematisk forventning, varians, distribusjonsfunksjon, bygge tetthetsgrafer og distribusjonsfunksjoner, finn.
Løsning: Først av alt, la oss merke oss at betingelsen ikke sier noe om arten av den tilfeldige variabelen. Tilstedeværelsen av en eksponent i seg selv betyr ikke noe: det kan vise seg, for eksempel, veiledende eller til og med vilkårlig kontinuerlig distribusjon. Og derfor må "normaliteten" til fordelingen fortsatt begrunnes:
Siden funksjonen ![]() bestemt kl noen reell verdi , og den kan reduseres til formen , så fordeles den tilfeldige variabelen etter normalloven.
bestemt kl noen reell verdi , og den kan reduseres til formen , så fordeles den tilfeldige variabelen etter normalloven.
Her går vi. For dette velg en komplett firkant og organisere tre-etasjers brøkdel:
Sørg for å utføre en sjekk, og returner indikatoren til sin opprinnelige form:
, som er det vi ønsket å se.
Dermed:  - Av driftsregel med fullmakter"klype av" Og her kan du umiddelbart skrive ned de åpenbare numeriske egenskapene:
- Av driftsregel med fullmakter"klype av" Og her kan du umiddelbart skrive ned de åpenbare numeriske egenskapene:
La oss nå finne verdien av parameteren. Siden normalfordelingsmultiplikatoren har formen og , da:  , hvorfra vi uttrykker og erstatter funksjonen vår:
, hvorfra vi uttrykker og erstatter funksjonen vår:  , hvoretter vi igjen vil gå gjennom opptaket med øynene og sørge for at den resulterende funksjonen har formen
, hvoretter vi igjen vil gå gjennom opptaket med øynene og sørge for at den resulterende funksjonen har formen  .
.
La oss bygge en tetthetsgraf: 
og distribusjonsfunksjonsgraf  :
:
Hvis du ikke har Excel eller en vanlig kalkulator for hånden, kan den siste grafen enkelt bygges manuelt! På et tidspunkt får fordelingsfunksjonen en verdi og finnes her
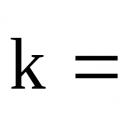 Reaksjonshastighetskonstant Retningslinjer for laboratoriearbeid
Reaksjonshastighetskonstant Retningslinjer for laboratoriearbeid Finnes det liv etter døden?
Finnes det liv etter døden? Forskere: Jorden er et "romfengsel" for menneskehetens forskere: Jorden er et romfengsel i universet
Forskere: Jorden er et "romfengsel" for menneskehetens forskere: Jorden er et romfengsel i universet