Variasjon av konstanter. ODE
Forelesning 44. Lineære inhomogene likninger av andre orden. Metode for variasjon av vilkårlige konstanter. Lineære inhomogene ligninger av andre orden med konstante koeffisienter. (spesiell høyre side).
Sosiale transformasjoner. Stat og kirke.
Sosial politikk Bolsjevikene ble i stor grad diktert av deres klassetilnærming. Ved dekret av 10. november 1917 ble klassesystemet ødelagt, førrevolusjonære rekker, titler og utmerkelser ble avskaffet. Valg av dommere er etablert; sekularisering av sivile stater ble gjennomført. Gratis utdanning og medisinsk behandling ble opprettet (dekret av 31. oktober 1918). Kvinner ble gitt like rettigheter som menn (dekret av 16. og 18. desember 1917). Dekretet om ekteskap introduserte institusjonen for sivilt ekteskap.
Ved dekret fra Folkekommissærrådet av 20. januar 1918 ble kirken skilt fra staten og fra utdanningssystemet. Det meste av kirkens eiendom ble konfiskert. Patriark av Moskva og All Rus' Tikhon (valgt 5. november 1917) 19. januar 1918 anatematiserte sovjetmakten og oppfordret til kamp mot bolsjevikene.
Tenk på en lineær inhomogen andreordens ligning
Strukturen til den generelle løsningen av en slik ligning bestemmes av følgende teorem:
Teorem 1. Den generelle løsningen av den inhomogene ligningen (1) er representert som summen av en bestemt løsning av denne ligningen og den generelle løsningen av den tilsvarende homogene ligningen
Bevis. Det er nødvendig å bevise at beløpet
Det er felles vedtak ligning (1). La oss først bevise at funksjon (3) er en løsning på ligning (1).
Sette inn summen i ligning (1) i stedet for på, vil ha
Siden det er en løsning på ligning (2), er uttrykket i de første parentesene identisk lik null. Siden det er en løsning på ligning (1), er uttrykket i andre parentes lik f(x). Derfor er likhet (4) en identitet. Dermed er første del av teoremet bevist.
La oss bevise det andre utsagnet: uttrykk (3) er generell løsning på ligning (1). Vi må bevise at de vilkårlige konstantene som er inkludert i dette uttrykket kan velges slik at startbetingelsene er oppfylt:
uansett hva tallene er x 0, y 0 og (hvis bare x 0 ble hentet fra området der funksjonene en 1, en 2 Og f(x) kontinuerlige).
Legger merke til at det kan representeres i skjemaet . Da vil vi, basert på forhold (5), ha
La oss løse dette systemet og bestemme C 1 Og C 2. La oss omskrive systemet i formen:
Merk at determinanten for dette systemet er Wronski-determinanten for funksjonene kl 1 Og kl 2 på punktet x=x 0. Siden disse funksjonene er lineært uavhengige av betingelse, er ikke Wronski-determinanten lik null; derfor har system (6) en klar løsning C 1 Og C 2, dvs. det er slike betydninger C 1 Og C 2, under hvilken formel (3) bestemmer løsningen til ligning (1) som tilfredsstiller de gitte startbetingelsene. Q.E.D.
La oss gå videre til den generelle metoden for å finne partielle løsninger på en inhomogen ligning.
La oss skrive den generelle løsningen av den homogene ligningen (2)
Vi vil se etter en spesiell løsning på den inhomogene ligningen (1) i formen (7), med tanke på C 1 Og C 2 som noen ennå ukjente funksjoner fra X.
La oss skille likhet (7):
La oss velge funksjonene du leter etter C 1 Og C 2 slik at likheten holder
Hvis vi tar hensyn til denne tilleggsbetingelsen, vil den første deriverte ha formen
Ved å differensiere dette uttrykket finner vi:
Setter vi inn i ligning (1), får vi
Uttrykkene i de to første parentesene blir null, siden y 1 Og y 2– løsninger av en homogen ligning. Derfor tar den siste likheten formen
Dermed vil funksjon (7) være en løsning på den inhomogene ligningen (1) hvis funksjonene C 1 Og C 2 tilfredsstille ligning (8) og (9). La oss lage et likningssystem fra likningene (8) og (9).
Siden determinanten for dette systemet er Wronski-determinanten for lineært uavhengige løsninger y 1 Og y 2 ligning (2), så er den ikke lik null. Derfor, løse systemet, vil vi finne både visse funksjoner av X:
Ved å løse dette systemet finner vi , hvorfra vi, som et resultat av integrasjon, får . Deretter erstatter vi funnfunksjonene i formelen, vi får en generell løsning på den inhomogene ligningen, hvor er vilkårlige konstanter.
Metoden for variasjon av vilkårlige konstanter brukes til å løse inhomogene differensialligninger. Denne leksjonen er ment for de elevene som allerede er mer eller mindre godt kjent med temaet. Hvis du så vidt begynner å bli kjent med fjernkontroll, dvs. Hvis du er en tekanne, anbefaler jeg å starte med den første leksjonen: Første ordens differensialligninger. Eksempler på løsninger. Og hvis du allerede er ferdig, ber vi deg forkaste den mulige forforståelsen om at metoden er vanskelig. Fordi det er enkelt.
I hvilke tilfeller brukes metoden for variasjon av vilkårlige konstanter?
1) Metoden for variasjon av en vilkårlig konstant kan brukes til å løse lineær inhomogen DE av 1. orden. Siden ligningen er av første orden, så er konstanten også en.
2) Metoden for variasjon av vilkårlige konstanter brukes til å løse noen lineære inhomogene andre ordens ligninger. Her varierer to konstanter.
Det er logisk å anta at leksjonen vil bestå av to avsnitt... Så jeg skrev denne setningen, og i omtrent 10 minutter tenkte jeg smertefullt på hvilken annen smart dritt jeg kunne legge til for en jevn overgang til praktiske eksempler. Men av en eller annen grunn har jeg ingen tanker etter ferien, selv om jeg ikke ser ut til å ha misbrukt noe. La oss derfor gå rett til første avsnitt.
Metode for variasjon av en vilkårlig konstant
for en førsteordens lineær inhomogen ligning
Før du vurderer metoden for variasjon av en vilkårlig konstant, er det tilrådelig å være kjent med artikkelen Lineære differensialligninger av første orden. I den leksjonen øvde vi første løsning inhomogen 1. ordens DE. Denne første løsningen, minner jeg om, heter erstatningsmetode eller Bernoulli metode(ikke å forveksle med Bernoullis ligning!!!)
Nå skal vi se andre løsning– metode for variasjon av en vilkårlig konstant. Jeg vil bare gi tre eksempler, og jeg vil ta dem fra den ovennevnte leksjonen. Hvorfor så få? For faktisk vil løsningen på den andre måten være veldig lik løsningen på den første måten. I tillegg, ifølge mine observasjoner, brukes metoden for variasjon av vilkårlige konstanter sjeldnere enn erstatningsmetoden.
Eksempel 1
![]()
(Avviker fra eksempel nr. 2 i leksjonen Lineære inhomogene differensialligninger av 1. orden)
Løsning: Denne ligningen er lineær inhomogen og har en kjent form: ![]()
På det første trinnet er det nødvendig å løse en enklere ligning: ![]()
Det vil si at vi dumt tilbakestiller høyre side og skriver null i stedet.
Ligningen ![]() Jeg ringer hjelpeligning.
Jeg ringer hjelpeligning.
I dette eksemplet må du løse følgende hjelpeligning:
Før oss separerbar ligning, hvis løsning (håper jeg) ikke lenger er vanskelig for deg: 
Dermed: ![]() – generell løsning av hjelpeligningen.
– generell løsning av hjelpeligningen.
På det andre trinnet vi vil erstatte noen konstante for nå ukjent funksjon som avhenger av "x":
Derav navnet på metoden - vi varierer konstanten. Alternativt kan konstanten være en funksjon som vi nå må finne.
I opprinnelig inhomogen ligning ![]() la oss gjøre en erstatning:
la oss gjøre en erstatning:
La oss erstatte og ![]() inn i ligningen
inn i ligningen ![]() :
:
Kontrollpunkt – de to termene på venstre side avbryter. Hvis dette ikke skjer, bør du se etter feilen ovenfor.
Som et resultat av erstatningen ble det oppnådd en ligning med separerbare variabler. Vi skiller variablene og integrerer.
For en velsignelse, eksponentene avbryter også:
Vi legger til en "normal" konstant til funnfunksjonen:
På siste trinn La oss huske erstatningen vår:
Funksjonen er nettopp funnet!
Så den generelle løsningen er: 
Svar: felles beslutning: ![]()
Skriver du ut de to løsningene vil du lett legge merke til at vi i begge tilfeller fant de samme integralene. Den eneste forskjellen ligger i løsningsalgoritmen.
Nå for noe mer komplisert, vil jeg også kommentere det andre eksemplet:
Eksempel 2
Finn den generelle løsningen på differensialligningen ![]()
(Avviker fra eksempel nr. 8 i leksjonen Lineære inhomogene differensialligninger av 1. orden)
Løsning: La oss redusere likningen til formen ![]() :
:
La oss tilbakestille høyre side og løse hjelpeligningen:
Generell løsning på hjelpeligningen:
I den inhomogene ligningen gjør vi erstatningen:
I henhold til produktdifferensieringsregelen: ![]()
La oss erstatte og ![]() inn i den opprinnelige inhomogene ligningen:
inn i den opprinnelige inhomogene ligningen:
De to begrepene på venstre side avbryter, noe som betyr at vi er på rett spor: 
La oss integrere etter deler. Den smakfulle bokstaven fra integrasjonsformelen er allerede involvert i løsningen, så vi bruker for eksempel bokstavene "a" og "be":
![]()
La oss nå huske erstatningen:
Svar: felles beslutning:
Og ett eksempel for uavhengig avgjørelse:
Eksempel 3
Finn en spesiell løsning på differensialligningen som tilsvarer den gitte startbetingelsen.
,
(Avviker fra eksempel nr. 4 i leksjonen Lineære inhomogene differensialligninger av 1. orden)
Løsning:
Denne DE er lineær inhomogen. Vi bruker metoden for variasjon av vilkårlige konstanter. La oss løse hjelpeligningen:
Vi skiller variablene og integrerer: 
Felles avgjørelse: ![]()
I den inhomogene ligningen gjør vi erstatningen: ![]()
La oss utføre erstatningen: 
Så den generelle løsningen er: ![]()
La oss finne en spesiell løsning som tilsvarer den gitte starttilstanden: ![]()
Svar: privat løsning:
Løsningen på slutten av timen kan tjene som eksempel for å fullføre oppgaven.
Metode for variasjon av vilkårlige konstanter
for en lineær inhomogen andreordens ligning
med konstante koeffisienter
Jeg har ofte hørt den oppfatningen at metoden for å variere vilkårlige konstanter for en annenordens ligning ikke er en enkel ting. Men jeg antar følgende: mest sannsynlig virker metoden vanskelig for mange fordi den ikke forekommer så ofte. Men i virkeligheten er det ingen spesielle vanskeligheter - forløpet av avgjørelsen er tydelig, gjennomsiktig og forståelig. Og vakker.
For å mestre metoden er det ønskelig å kunne løse inhomogene andreordensligninger ved å velge en bestemt løsning basert på formen på høyre side. Denne metoden er omtalt i detalj i artikkelen. Inhomogene 2. ordens DE-er. Vi husker at en andreordens lineær inhomogen ligning med konstante koeffisienter har formen:
Valgmetoden, som ble diskutert i leksjonen ovenfor, fungerer bare i et begrenset antall tilfeller når høyresiden inneholder polynomer, eksponentialer, sinus og cosinus. Men hva skal man gjøre når til høyre for eksempel er en brøk, logaritme, tangent? I en slik situasjon kommer metoden for variasjon av konstanter til unnsetning.
Eksempel 4
Finn den generelle løsningen på en andreordens differensialligning ![]()
Løsning: Det er en brøkdel på høyre side av denne ligningen, så vi kan umiddelbart si at metoden for å velge en bestemt løsning ikke fungerer. Vi bruker metoden for variasjon av vilkårlige konstanter.
Det er ingen tegn til tordenvær; begynnelsen av løsningen er helt vanlig:
Vi finner felles vedtak passende homogen ligninger: ![]()
La oss komponere og løse den karakteristiske ligningen: ![]()
![]() - konjugerte komplekse røtter oppnås, så den generelle løsningen er:
- konjugerte komplekse røtter oppnås, så den generelle løsningen er:
Vær oppmerksom på oversikten over den generelle løsningen - hvis det er parenteser, åpne dem.
Nå gjør vi nesten det samme trikset som for førsteordensligningen: vi varierer konstantene, og erstatter dem med ukjente funksjoner. Det er, generell løsning av inhomogene vi vil se etter ligninger i formen:
Hvor - for nå ukjente funksjoner.

Det ser ut som en husholdningsavfallsplass, men nå skal vi ordne opp i alt.
De ukjente er avledet av funksjonene. Målet vårt er å finne deriverte, og de funnet deriverte må tilfredsstille både den første og andre ligningen i systemet.
Hvor kommer "grekerne" fra? Storken bringer dem. Vi ser på den generelle løsningen oppnådd tidligere og skriver:
La oss finne derivatene:
De venstre delene er behandlet. Hva er til høyre?
er høyre side av den opprinnelige ligningen, i dette tilfellet:
Koeffisienten er koeffisienten til den andre deriverte:
I praksis nesten alltid, og vårt eksempel er intet unntak.
Alt er klart, nå kan du lage et system: 
Systemet er vanligvis løst i henhold til Cramers formler ved hjelp av standardalgoritmen. Den eneste forskjellen er at i stedet for tall har vi funksjoner.
La oss finne hoveddeterminanten for systemet: 
Hvis du har glemt hvordan to-og-to-determinanten avsløres, se leksjonen Hvordan beregne determinanten? Linken fører til skammestyret =)
Altså: dette betyr at systemet har en unik løsning.
Finne den deriverte: 
Men det er ikke alt, så langt har vi bare funnet den deriverte.
Selve funksjonen gjenopprettes ved integrasjon:
La oss se på den andre funksjonen: 
![]()
![]()
Her legger vi til en "normal" konstant
På sluttfasen av løsningen husker vi i hvilken form vi lette etter en generell løsning på den inhomogene ligningen? I slike:
Funksjonene du trenger er nettopp funnet! ![]()
Alt som gjenstår er å utføre substitusjonen og skrive ned svaret:
Svar: felles beslutning:
I prinsippet kunne svaret ha utvidet parentesen.
En fullstendig kontroll av svaret utføres i henhold til standardskjemaet, som ble diskutert i leksjonen. Inhomogene 2. ordens DE-er. Men verifiseringen vil ikke være lett, siden det er nødvendig å finne ganske tunge derivater og utføre tungvint substitusjon. Dette er en ubehagelig egenskap når du løser slike diffusorer.
Eksempel 5
Løs en differensialligning ved å variere vilkårlige konstanter
![]()
Dette er et eksempel du kan løse på egen hånd. Faktisk er det på høyre side også en brøkdel. La oss huske trigonometrisk formel, forresten, det må påføres under løsningen.
Metoden for variasjon av vilkårlige konstanter er den mest universelle metoden. Den kan løse enhver ligning som kan løses metode for å velge en bestemt løsning basert på formen til høyre side. Spørsmålet oppstår: hvorfor ikke bruke metoden for variasjon av vilkårlige konstanter der også? Svaret er åpenbart: valget av en bestemt løsning, som ble diskutert i klassen Inhomogene andre ordens ligninger, øker betydelig hastighet på løsningen og forkorter opptaket - ikke noe oppstyr med determinanter og integraler.
La oss se på to eksempler med Cauchy problem.
Eksempel 6
Finn en spesiell løsning på differensialligningen som tilsvarer de gitte startbetingelsene
![]() ,
, ![]()
Løsning: Igjen brøken og eksponenten i interessant sted.
Vi bruker metoden for variasjon av vilkårlige konstanter.
Vi finner felles vedtak passende homogen ligninger: ![]()
![]() – forskjellige reelle røtter oppnås, så den generelle løsningen er:
– forskjellige reelle røtter oppnås, så den generelle løsningen er:
Generell løsning av inhomogene vi ser etter ligninger i formen: , hvor – for nå ukjente funksjoner.
La oss lage et system: 
I dette tilfellet:
,
Finne derivater: ![]() ,
, ![]()
![]()
Dermed: 
La oss løse systemet ved å bruke Cramers formler:
, som betyr at systemet har en unik løsning.


Vi gjenoppretter funksjonen ved integrasjon:
Brukes her metode for å subsumere en funksjon under differensialtegnet.


Vi gjenoppretter den andre funksjonen ved integrering: ![]()
Dette integralet er løst variabel erstatningsmetode:
Fra selve erstatningen uttrykker vi:
Dermed: ![]()
![]()
Denne integralen kan finnes komplett kvadratisk utvinningsmetode, men i eksempler med diffusorer foretrekker jeg å utvide fraksjonen metode usikre koeffisienter
:
Begge funksjonene funnet:
Som et resultat er den generelle løsningen på den inhomogene ligningen:
La oss finne en spesiell løsning som tilfredsstiller startbetingelsene ![]() .
.
Teknisk sett utføres søket etter en løsning på en standard måte, som ble diskutert i artikkelen Inhomogene differensialligninger av andre orden.
Hold fast, nå vil vi finne den deriverte av den funnet generelle løsningen:
Dette er en skam. Det er ikke nødvendig å forenkle det; det er lettere å umiddelbart lage et ligningssystem. I henhold til de opprinnelige forholdene ![]() :
:

La oss erstatte de funnet verdiene til konstantene ![]() til den generelle løsningen:
til den generelle løsningen:
I svaret kan logaritmene pakkes litt.
Svar: privat løsning: ![]()
Som du kan se, kan det oppstå vanskeligheter i integraler og derivater, men ikke i algoritmen til selve metoden for variasjon av vilkårlige konstanter. Det er ikke jeg som skremte deg, det er hele Kuznetsovs samling!
For avslapning, et siste, enklere eksempel for å løse det selv:
Eksempel 7
Løs Cauchy-problemet
![]() ,
, ![]()
Eksemplet er enkelt, men kreativt, når du lager et system, se nøye på det før du bestemmer deg ;-),
![]()


![]()
Som et resultat er den generelle løsningen:
La oss finne en spesiell løsning som tilsvarer startbetingelsene ![]() .
.
![]()

La oss erstatte de funnet verdiene til konstantene i den generelle løsningen:
Svar: privat løsning:
Metoden for variasjon av en vilkårlig konstant, eller Lagrange-metoden, er en annen måte å løse førsteordens lineære differensialligninger og Bernoulli-ligningen.
Lineære differensialligninger av første orden er likninger av formen y’+p(x)y=q(x). Hvis det er en null på høyre side: y’+p(x)y=0, så er dette en lineær homogen 1. ordens ligning. Følgelig er en ligning med en høyreside som ikke er null, y’+p(x)y=q(x), heterogen 1. ordens lineær ligning.
Metode for variasjon av en vilkårlig konstant (Lagrange-metoden) er som følgende:
1) Vi leter etter en generell løsning på den homogene ligningen y’+p(x)y=0: y=y*.
2) I den generelle løsningen betrakter vi C ikke som en konstant, men en funksjon av x: C = C (x). Vi finner den deriverte av den generelle løsningen (y*)’ og erstatter det resulterende uttrykket for y* og (y*)’ i starttilstanden. Fra den resulterende ligningen finner vi funksjonen C(x).
3) I den generelle løsningen av den homogene ligningen, i stedet for C, erstatter vi det funnet uttrykket C(x).
La oss se på eksempler på metoden for å variere en vilkårlig konstant. La oss ta de samme oppgavene som i, sammenligne fremdriften til løsningen og forsikre oss om at svarene som er oppnådd er sammenfallende.
1) y'=3x-y/x
La oss omskrive ligningen i standardform (i motsetning til Bernoullis metode, hvor vi trengte notasjonsformen bare for å se at ligningen er lineær).
y’+y/x=3x (I). Nå fortsetter vi etter planen.
1) Løs den homogene ligningen y’+y/x=0. Dette er en ligning med separerbare variabler. Se for deg y’=dy/dx, erstatte: dy/dx+y/x=0, dy/dx=-y/x. Vi multipliserer begge sider av ligningen med dx og deler på xy≠0: dy/y=-dx/x. La oss integrere:
2) I den resulterende generelle løsningen av den homogene ligningen vil vi betrakte C ikke som en konstant, men en funksjon av x: C=C(x). Herfra
Vi erstatter de resulterende uttrykkene i betingelse (I):
La oss integrere begge sider av ligningen:
her er C allerede en ny konstant.
3) I den generelle løsningen av den homogene ligningen y=C/x, der vi antok C=C(x), det vil si y=C(x)/x, erstatter vi det funnet uttrykket x³ i stedet for C(x) +C: y=(x3 +C)/x eller y=x²+C/x. Vi fikk samme svar som ved løsning etter Bernoullis metode.
Svar: y=x²+C/x.
2) y’+y=cosx.
Her er ligningen allerede skrevet i standardform, det er ikke nødvendig å transformere den.
1) Løs den homogene lineære ligningen y’+y=0: dy/dx=-y; dy/y=-dx. La oss integrere:
For å få en mer praktisk form for notasjon, tar vi eksponenten til potensen av C som den nye C:
Denne transformasjonen ble utført for å gjøre det mer praktisk å finne derivatet.
2) I den resulterende generelle løsningen av den lineære homogene ligningen betrakter vi C ikke som en konstant, men en funksjon av x: C=C(x). Under denne betingelsen
![]()
Vi erstatter de resulterende uttrykkene y og y' i betingelsen:
Multipliser begge sider av ligningen med
Vi integrerer begge sider av ligningen ved å bruke formelen for integrering etter deler, vi får:
Her er ikke C lenger en funksjon, men en ordinær konstant.
3) I den generelle løsningen av den homogene ligningen
erstatte funnfunksjonen C(x):
Vi fikk samme svar som ved løsning etter Bernoullis metode.
Metoden for variasjon av en vilkårlig konstant er også anvendelig for å løse.
y'x+y=-xy².
Vi bringer likningen til standardform: y’+y/x=-y² (II).
1) Løs den homogene ligningen y’+y/x=0. dy/dx=-y/x. Vi multipliserer begge sider av ligningen med dx og deler på y: dy/y=-dx/x. La oss nå integrere:
Vi erstatter de resulterende uttrykkene i betingelse (II):
La oss forenkle:
![]()
Vi fikk en likning med separerbare variabler for C og x:
![]()
![]()
Her er C allerede en vanlig konstant. Under integrasjonsprosessen skrev vi ganske enkelt C i stedet for C(x), for ikke å overbelaste notasjonen. Og på slutten kom vi tilbake til C(x), for ikke å forveksle C(x) med den nye C.
3) I den generelle løsningen av den homogene ligningen y=C(x)/x erstatter vi den funnet funksjonen C(x):
![]()
Vi fikk det samme svaret som da vi løste det med Bernoulli-metoden.
![]()
Eksempler på selvtest:
1. La oss omskrive ligningen i standardform: y’-2y=x.
1) Løs den homogene ligningen y’-2y=0. y’=dy/dx, derav dy/dx=2y, multipliser begge sider av ligningen med dx, del på y og integrer:
Herfra finner vi y:
Vi erstatter uttrykkene for y og y' i betingelsen (for korthets skyld bruker vi C i stedet for C(x) og C' i stedet for C"(x)):
For å finne integralet på høyre side bruker vi formelen for integrering etter deler:
![]()
Nå erstatter vi u, du og v i formelen:
Her er C =konst.
3) Nå erstatter vi homogen i løsningen
En metode for å løse lineære inhomogene differensialligninger av høyere orden med konstante koeffisienter ved hjelp av metoden for variasjon av Lagrange-konstanter vurderes. Lagrange-metoden er også anvendelig for å løse alle lineære inhomogene ligninger hvis det grunnleggende systemet med løsninger til den homogene ligningen er kjent.
InnholdSe også:
Lagrangemetode (variasjon av konstanter)
Tenk på en lineær inhomogen differensialligning med konstante koeffisienter av vilkårlig n-te orden:
(1)
.
Metoden for variasjon av en konstant, som vi vurderte for en førsteordens ligning, er også anvendelig for ligninger av høyere orden.
Løsningen utføres i to trinn. I det første trinnet forkaster vi høyre side og løser den homogene ligningen. Som et resultat får vi en løsning som inneholder n vilkårlige konstanter. På det andre trinnet varierer vi konstantene. Det vil si at vi tror at disse konstantene er funksjoner av den uavhengige variabelen x og finner formen til disse funksjonene.
Selv om vi vurderer ligninger med konstante koeffisienter her, men Lagranges metode er også anvendelig for å løse alle lineære inhomogene ligninger. For å gjøre dette må det grunnleggende løsningssystemet til den homogene ligningen være kjent.
Trinn 1. Løse den homogene ligningen
Som i tilfellet med førsteordens ligninger, ser vi først etter den generelle løsningen av den homogene ligningen, og likestiller den høyre inhomogene siden til null:
(2)
.
Den generelle løsningen på denne ligningen er:
(3)
.
Her er vilkårlige konstanter; - n lineært uavhengige løsninger av homogen likning (2), som danner et grunnleggende system av løsninger til denne likningen.
Trinn 2. Variasjon av konstanter - erstatte konstanter med funksjoner
På det andre trinnet vil vi ta for oss variasjonen av konstanter. Med andre ord vil vi erstatte konstantene med funksjoner til den uavhengige variabelen x:
.
Det vil si at vi ser etter en løsning på den opprinnelige ligningen (1) i følgende form:
(4)
.
Hvis vi erstatter (4) med (1), får vi én differensialligning for n funksjoner. I dette tilfellet kan vi koble disse funksjonene med tilleggsligninger. Da får du n ligninger som n funksjoner kan bestemmes ut fra. Ytterligere ligninger kan skrives forskjellige måter. Men vi skal gjøre dette slik at løsningen har den enkleste formen. For å gjøre dette, når du differensierer, må du likestille med null termene som inneholder deriverte av funksjonene. La oss demonstrere dette.
For å erstatte den foreslåtte løsningen (4) i den opprinnelige ligningen (1), må vi finne de deriverte av de første n ordenene til funksjonen skrevet i formen (4). Vi skiller (4) ved å bruke reglene for differensiering av sum og produkt:
.
La oss gruppere medlemmene. Først skriver vi ned begrepene med derivater av , og deretter begrepene med derivater av :
.
La oss pålegge funksjonene den første betingelsen:
(5.1)
.
Da vil uttrykket for den første deriverte med hensyn til ha en enklere form:
(6.1)
.
Ved å bruke samme metode finner vi den andre deriverte:
.
La oss pålegge funksjonene en annen betingelse:
(5.2)
.
Deretter
(6.2)
.
Og så videre. I tilleggsbetingelser, likestiller vi termer som inneholder deriverte av funksjoner til null.
Så hvis vi velger følgende tilleggsligninger for funksjonene:
(5.k) ,
da vil de første deriverte med hensyn til ha den enkleste formen:
(6.k) .
Her .
Finn den n-te deriverte:
(6.n)
.
Bytt inn i den opprinnelige ligningen (1):
(1)
;
.
La oss ta i betraktning at alle funksjoner tilfredsstiller ligning (2):
.
Da gir summen av ledd som inneholder null null. Som et resultat får vi:
(7)
.
Som et resultat fikk vi et system lineære ligninger for derivater:
(5.1)
;
(5.2)
;
(5.3)
;
. . . . . . .
(5.n-1) ;
(7′) .
Ved å løse dette systemet finner vi uttrykk for deriverte som en funksjon av x. Ved å integrere får vi:
.
Her er konstanter som ikke lenger er avhengige av x. Ved å sette inn i (4), får vi en generell løsning på den opprinnelige ligningen.
Legg merke til at for å bestemme verdiene til derivatene, brukte vi aldri det faktum at koeffisientene a i er konstante. Derfor Lagranges metode er anvendelig for å løse alle lineære inhomogene ligninger, hvis det fundamentale systemet av løsninger til den homogene ligningen (2) er kjent.
Eksempler
Løs likninger ved å bruke metoden for variasjon av konstanter (Lagrange).
Løsning av eksempler > > >
Løse ligninger av høyere orden ved hjelp av Bernoulli-metoden
Løse lineære inhomogene differensialligninger av høyere orden med konstante koeffisienter ved lineær substitusjon
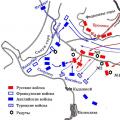 Slaget ved Balaclava Slaget ved Balaclava
Slaget ved Balaclava Slaget ved Balaclava Keiser Paul I og hans favoritt Ivan Pavlovich Kutaisov
Keiser Paul I og hans favoritt Ivan Pavlovich Kutaisov Prins Vsevolod III Big Nest Relations med Novgorod
Prins Vsevolod III Big Nest Relations med Novgorod