Hvordan finne arealet til en polygon? Hvordan finne ut arealet til en polygon? Arealet av polygonet.
I denne artikkelen vil vi snakke om hvordan du uttrykker arealet til en polygon som en sirkel kan skrives inn i, gjennom radiusen til denne sirkelen. Det er verdt å merke seg med en gang at ikke alle polygoner kan passe til en sirkel. Imidlertid, hvis dette er mulig, blir formelen som arealet til en slik polygon beregnes med, veldig enkel. Les denne artikkelen til slutten eller se den vedlagte videoopplæringen, og du vil lære hvordan du uttrykker arealet til en polygon i form av radiusen til sirkelen som er innskrevet i den.
Formel for arealet til en polygon i form av radiusen til den innskrevne sirkelen
La oss tegne en polygon EN 1 EN 2 EN 3 EN 4 EN 5, ikke nødvendigvis riktig, men en som en sirkel kan skrives inn i. La meg minne deg på at en innskrevet sirkel er en sirkel som berører alle sider av polygonet. På bildet er det en grønn sirkel med et senter i punktet O:
Vi tok 5-gon som eksempel her. Men faktisk er dette ikke av vesentlig betydning, siden det ytterligere beviset er gyldig for både en 6-gon og en 8-gon, og generelt for enhver vilkårlig "gon".
Hvis du kobler midten av den innskrevne sirkelen med alle toppunktene i polygonet, så vil den bli delt inn i like mange trekanter som det er toppunkter i den gitte polygonen. I vårt tilfelle: for 5 trekanter. Hvis vi kobler sammen prikken O med alle tangenspunkter i den innskrevne sirkelen med sidene til polygonet, får du 5 segmenter (i figuren under er disse segmenter Åh 1 , Åh 2 , Åh 3 , Åh 4 og Åh 5), som er lik radiusen til sirkelen og vinkelrett på sidene av polygonen de er tegnet til. Det siste er sant, siden radiusen trukket til kontaktpunktet er vinkelrett på tangenten:
Hvordan finne arealet av vår omskrevne polygon? Svaret er enkelt. Du må legge sammen arealene til alle de resulterende trekantene:
La oss vurdere hva arealet til en trekant er. På bildet nedenfor er det uthevet i gult:
Det er lik halvparten av produktet av basen EN 1 EN 2 til høyden Åh 1 trukket til denne basen. Men, som vi allerede har funnet ut, er denne høyden lik radiusen til den innskrevne sirkelen. Det vil si at formelen for arealet av en trekant har formen: ![]() , Hvor r— radius av den innskrevne sirkelen. Arealene til alle gjenværende trekanter finnes på samme måte. Som et resultat er det nødvendige arealet av polygonet lik:
, Hvor r— radius av den innskrevne sirkelen. Arealene til alle gjenværende trekanter finnes på samme måte. Som et resultat er det nødvendige arealet av polygonet lik:
Det kan sees at i alle termer av denne summen er det en felles faktor som kan tas ut av parentes. Resultatet blir følgende uttrykk:
Det vil si at det som gjenstår i parentes er ganske enkelt summen av alle sider av polygonet, det vil si dens omkrets P. Oftest i denne formelen erstattes uttrykket ganske enkelt med s og de kaller denne bokstaven "semi-perimeter". Som et resultat tar den endelige formelen formen:
Det vil si at arealet av en polygon som en sirkel med kjent radius er innskrevet i, er lik produktet av denne radiusen og polygonens halve omkrets. Dette er resultatet vi siktet oss til.
Til slutt vil han merke seg at en sirkel alltid kan skrives inn i en trekant, som er et spesialtilfelle av en polygon. Derfor kan denne formelen alltid brukes for en trekant. For andre polygoner med mer enn 3 sider, må du først sørge for at en sirkel kan skrives inn i dem. I så fall kan du trygt bruke dette enkel formel og bruk den til å finne arealet til denne polygonen.
Materiale utarbeidet av Sergey Valerievich
Alle som studerte matematikk og geometri på skolen kan disse vitenskapene i det minste overfladisk. Men over tid, hvis du ikke praktiserer dem, blir kunnskap glemt. Mange tror til og med at de bare kastet bort tiden på å studere geometriske beregninger. De tar imidlertid feil. Tekniske arbeidere utfører daglig arbeid knyttet til geometriske beregninger. Når det gjelder å beregne arealet til en polygon, finner denne kunnskapen også sin anvendelse i livet. De vil være nødvendige i det minste for å beregne arealet av landet. Så la oss lære hvordan du finner arealet til en polygon.
Polygon definisjon
Først, la oss definere hva en polygon er. Det er flatt geometrisk figur, som ble dannet som et resultat av skjæringspunktet mellom tre eller flere rette linjer. En annen enkel definisjon: en polygon er en lukket polylinje. Naturligvis, når linjer skjærer, dannes skjæringspunkter deres antall er lik antallet linjer som danner polygonen. Skjæringspunktene kalles toppunkter, og segmentene dannet av rette linjer kalles sider av polygonet. Tilstøtende segmenter av en polygon er ikke på samme rette linje. Linjestykker som ikke er tilstøtende er de som ikke går gjennom felles punkter.
Summen av arealer av trekanter
Hvordan finne arealet til en polygon? Arealet til en polygon er det indre av planet som er dannet av skjæringspunktet mellom segmentene eller sidene av polygonet. Siden en polygon er en kombinasjon av figurer som en trekant, rombe, firkant, trapes, er det rett og slett ingen universell formel for å beregne arealet. I praksis er den mest universelle metoden for å dele en polygon i enklere figurer, hvis område ikke er vanskelig å finne. Ved å legge til summene av arealene til disse enkle figurene, oppnås arealet av polygonet.
Gjennom området til en sirkel
I de fleste tilfeller har en polygon en vanlig form og danner en figur med like sider og vinkler mellom seg. I dette tilfellet er det veldig enkelt å beregne arealet ved å bruke en innskrevet eller omskrevet sirkel. Hvis arealet av en sirkel er kjent, må det multipliseres med polygonens omkrets, og deretter det resulterende produktet delt på 2. Resultatet er en formel for å beregne arealet til en slik polygon: S = ½∙P∙r., der P er arealet av sirkelen, og r er omkretsen til polygonet.
Metoden for å dele en polygon i "praktiske" former er den mest populære innen geometri, den lar deg raskt og riktig finne arealet til en polygon. 4. klasse på ungdomsskolen studerer vanligvis slike metoder.
Geometriproblemer krever ofte beregning av arealet til en polygon. Dessuten kan den ha en ganske variert form - fra den kjente trekanten til en eller annen n-gon med et ufattelig antall hjørner. I tillegg kan disse polygonene være konvekse eller konkave. I hver spesifikk situasjon skal starte fra utseende tall. På denne måten kan du velge den optimale måten å løse problemet på. Figuren kan vise seg å være riktig, noe som i stor grad vil forenkle løsningen av problemet.
En liten teori om polygoner
Hvis du tegner tre eller flere kryssende linjer, danner de en bestemt figur. Det er hun som er polygonet. Basert på antall skjæringspunkter blir det klart hvor mange hjørner den vil ha. De gir navnet til den resulterende figuren. Det kan være:
En slik figur vil absolutt være preget av to posisjoner:
- Tilstøtende sider tilhører ikke den samme rette linjen.
- Ikke-tilstøtende har ingen felles punkter, det vil si at de ikke krysser hverandre.
For å forstå hvilke hjørner som er naboer, må du se om de tilhører samme side. Hvis ja, så naboene. Ellers kan de kobles sammen med et segment, som må kalles en diagonal. De kan bare utføres i polygoner som har mer enn tre hjørner.
Hvilke typer av dem finnes?
En polygon med mer enn fire hjørner kan være konveks eller konkav. Forskjellen mellom sistnevnte er at noen av toppunktene kan ligge på motsatte sider av en rett linje trukket gjennom en vilkårlig side av polygonet. I et konveks tilfelle ligger alle toppunktene alltid på samme side av en slik rett linje.
I et skolegeometrikurs er mesteparten av tiden viet til konvekse figurer. Derfor krever problemene å finne arealet til en konveks polygon. Så er det en formel i form av radiusen til den omskrevne sirkelen, som lar deg finne ønsket verdi for en hvilken som helst figur. I andre tilfeller er det ingen klar løsning. For en trekant er formelen én, men for en firkant eller trapes er den helt annerledes. I situasjoner der figuren er uregelmessig eller det er mange hjørner, er det vanlig å dele dem inn i enkle og kjente.
Hva skal jeg gjøre hvis figuren har tre eller fire hjørner?
I det første tilfellet vil det vise seg å være en trekant, og du kan bruke en av formlene:
- S = 1/2 * a * n, hvor a er siden, n er høyden til den;
- S = 1/2 * a * b * sin (A), hvor a, b er sidene i trekanten, A er vinkelen mellom de kjente sidene;
- S = √(p * (p - a) * (p - b) * (p - c)), der c er siden av trekanten, til de to som allerede er indikert, er p halvperimeteren, det vil si, summen av alle tre sidene delt på to.

En figur med fire hjørner kan vise seg å være et parallellogram:
- S = a * n;
- S = 1/2 * d 1 * d 2 * sin(α), hvor d 1 og d 2 er diagonaler, α er vinkelen mellom dem;
- S = a * i * sin(α).
Formel for arealet til en trapes: S = n * (a + b) / 2, hvor a og b er lengdene til basene.
Hva skal man gjøre med en vanlig polygon som har mer enn fire hjørner?
Til å begynne med er en slik figur preget av at alle sider er like. I tillegg har polygonet like vinkler.
Hvis du tegner en sirkel rundt en slik figur, vil dens radius falle sammen med segmentet fra midten av polygonet til en av toppunktene. Derfor, for å beregne arealet vanlig polygon med et vilkårlig antall hjørner, trenger du følgende formel:
S n = 1/2 * n * R n 2 * sin (360º/n), der n er antall toppunkter i polygonet.

Fra den er det enkelt å skaffe en som er nyttig for spesielle tilfeller:
- trekant: S = (3√3)/4 * R2;
- kvadrat: S = 2 * R2;
- sekskant: S = (3√3)/2 * R 2.
Situasjonen med feil figur
Løsningen på hvordan du finner ut arealet til en polygon hvis den ikke er vanlig og ikke kan tilskrives noen av de tidligere kjente figurene, er algoritmen:
- bryte den i enkle former, for eksempel trekanter, slik at de ikke krysser hverandre;
- beregne arealene deres ved å bruke en hvilken som helst formel;
- legge sammen alle resultatene.
Hva skal jeg gjøre hvis problemet gir koordinatene til toppunktene til en polygon?
Det vil si at et sett med tallpar er kjent for hvert punkt som begrenser sidene av figuren. Vanligvis skrives de som (x 1 ; y 1) for den første, (x 2 ; y 2) for den andre, og den n-te toppunktet har følgende verdier (x n ; y n). Deretter bestemmes arealet av polygonet som summen av n ledd. Hver av dem ser slik ut: ((y i+1 +y i)/2) * (x i+1 - x i). I dette uttrykket varierer i fra én til n.
Det er verdt å merke seg at tegnet på resultatet vil avhenge av gjennomgangen av figuren. Når du bruker formelen ovenfor og beveger deg med klokken, vil svaret være negativt.

Eksempeloppgave
Betingelse. Koordinatene til toppunktene er spesifisert av følgende verdier (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Du må beregne arealet til en polygon.
Løsning. I henhold til formelen ovenfor vil det første leddet være lik (1,8 + 0,6)/2 * (3,6 - 2,1). Her trenger du bare å ta verdiene for Y og X fra det andre og første punktet. En enkel utregning vil føre til resultatet 1.8.
Det andre leddet oppnås på samme måte: (2,2 + 1,8)/2 * (2,3 - 3,6) = -2,6. Når du løser slike problemer, ikke vær redd for negative mengder. Alt går som det skal. Dette er planlagt.
Verdiene for tredje (0,29), fjerde (-6,365) og femte ledd (2,96) oppnås på lignende måte. Da er det endelige området: 1,8 + (-2,6) + 0,29 + (-6,365) + 2,96 = - 3,915.

Råd for å løse et problem der en polygon er tegnet på rutete papir
Det som oftest er forvirrende er at dataene kun inneholder cellestørrelse. Men det viser seg at det ikke trengs mer informasjon. En anbefaling for å løse dette problemet er å dele figuren i mange trekanter og rektangler. Arealene deres er ganske enkle å beregne ut fra lengdene på sidene, som deretter enkelt kan legges sammen.
Men det er ofte en enklere tilnærming. Den består av å tegne en figur til et rektangel og beregne arealet. Beregn deretter arealene til de elementene som viste seg å være overflødige. Trekk dem fra den totale verdien. Dette alternativet innebærer noen ganger et litt mindre antall handlinger.
\[(\Large(\text(Grunnleggende fakta om området)))\]
Vi kan si at arealet til en polygon er en verdi som indikerer den delen av planet som en gitt polygon opptar. Arealmåleenheten er arealet til et kvadrat med en side på \(1\) cm, \(1\) mm, etc. (enhet kvadrat). Da vil arealet bli målt i henholdsvis cm\(^2\), mm\(^2\).
Med andre ord kan vi si at arealet til en figur er en mengde hvis numeriske verdi viser hvor mange ganger en kvadratisk enhet passer i en gitt figur.
Områdeegenskaper
1. Arealet til en hvilken som helst polygon er en positiv størrelse.
2. Like polygoner har like arealer.
3. Hvis en polygon består av flere polygoner, er arealet lik summen av arealene til disse polygonene.
4. Arealet av et kvadrat med siden \(a\) er lik \(a^2\) .
\[(\Large(\text(Areal av et rektangel og parallellogram)))\]
Teorem: Arealet av et rektangel
Arealet til et rektangel med sidene \(a\) og \(b\) er lik \(S=ab\) .
Bevis
La oss bygge rektangelet \(ABCD\) til en firkant med siden \(a+b\), som vist i figuren:
Denne firkanten består av et rektangel \(ABCD\), et annet like stort rektangel og to firkanter med sidene \(a\) og \(b\) . Slik,
\(\begin(multline*) S_(a+b)=2S_(\text(pr-k))+S_a+S_b \Leftrightarrow (a+b)^2=2S_(\text(pr-k))+ a^2+b^2 \Leftrightarrow\\ a^2+2ab+b^2=2S_(\text(pr-k))+a^2+b^2 \Rightarrow S_(\text(pr-k) )=ab \end(flerlinje*)\)
Definisjon
Høyden til et parallellogram er perpendikulæren trukket fra toppunktet på parallellogrammet til siden (eller til forlengelsen av siden) som ikke inneholder dette toppunktet.
For eksempel faller høyden \(BK\) på siden \(AD\) , og høyden \(BH\) faller på fortsettelsen av siden \(CD\) :

Teorem: Arealet av et parallellogram
Arealet til et parallellogram er lik produktet av høyden og siden som denne høyden er tegnet til.
Bevis
La oss tegne perpendikulære \(AB"\) og \(DC"\) som vist på figuren. Merk at disse perpendikulærene er lik høyden på parallellogrammet \(ABCD\) .

Da er \(AB"C"D\) et rektangel, derfor \(S_(AB"C"D)=AB"\cdot AD\) .
Merk at rette trekanter \(ABB"\) og \(DCC"\) er kongruente. Slik,
\(S_(ABCD)=S_(ABC"D)+S_(DCC")=S_(ABC"D)+S_(ABB")=S_(AB"C"D)=AB"\cdot AD.\)
\[(\Large(\tekst(Trekantareal)))\]
Definisjon
Vi vil kalle siden som høyden i trekanten er tegnet til, for trekantens basis.
Teorem
Arealet til en trekant er lik halvparten av produktet av basen og høyden trukket til denne basen.
Bevis
La \(S\) være arealet av trekanten \(ABC\) . La oss ta siden \(AB\) som basis av trekanten og tegne høyden \(CH\) . La oss bevise det \ La oss bygge trekanten \(ABC\) til parallellogrammet \(ABDC\) som vist i figuren:

Trekanter \(ABC\) og \(DCB\) er like på tre sider (\(BC\) er deres felles side, \(AB = CD\) og \(AC = BD\) som motsatte sider av parallellogrammet \ (ABDC\ )), så deres arealer er like. Derfor er arealet \(S\) av trekanten \(ABC\) lik halve arealet av parallellogrammet \(ABDC\), dvs. \(S = \dfrac(1)(2)AB\cdot CH\).
Teorem
Hvis to trekanter \(\triangle ABC\) og \(\triangle A_1B_1C_1\) har like høyder, så er deres arealer relatert til basene som disse høydene er tegnet til.

Konsekvens
Medianen til en trekant deler den i to trekanter med lik areal.
Teorem
Hvis to trekanter \(\triangle ABC\) og \(\triangle A_2B_2C_2\) hver har lik vinkel, så er deres områder relatert som produktet av sidene som danner denne vinkelen.

Bevis
La \(\vinkel A=\vinkel A_2\) . La oss kombinere disse vinklene som vist i figuren (punkt \(A\) justert med punkt \(A_2\)):

La oss finne høydene \(BH\) og \(C_2K\) .
Trekanter \(AB_2C_2\) og \(ABC_2\) har samme høyde \(C_2K\) , derfor: \[\dfrac(S_(AB_2C_2))(S_(ABC_2))=\dfrac(AB_2)(AB)\]
Trekanter \(ABC_2\) og \(ABC\) har samme høyde \(BH\), derfor: \[\dfrac(S_(ABC_2))(S_(ABC))=\dfrac(AC_2)(AC)\]
Multipliserer de to siste likhetene, får vi: \[\dfrac(S_(AB_2C_2))(S_(ABC))=\dfrac(AB_2\cdot AC_2)(AB\cdot AC) \qquad \text( eller ) \qquad \dfrac(S_(A_2B_2C_2))(S_ (ABC))=\dfrac(A_2B_2\cdot A_2C_2)(AB\cdot AC)\]
Pythagoras teorem
I en rettvinklet trekant er kvadratet av lengden på hypotenusen lik summen av kvadratene av lengdene på bena:

Det motsatte er også sant: hvis kvadratet av lengden på den ene siden i en trekant er lik summen av kvadratene av lengdene på de to andre sidene, så er en slik trekant rettvinklet.
Teorem
Kvadrat rettvinklet trekant lik halvparten av produktet av bena.
Teorem: Herons formel
La \(p\) være halvomkretsen av trekanten, \(a\) , \(b\) , \(c\) være lengdene på sidene, så er arealet \
\[(\Large(\tekst(Område med rombe og trapes)))\]
Kommentar
Fordi En rombe er et parallellogram, da gjelder samme formel for den, dvs. Arealet til en rombe er lik produktet av høyden og siden som denne høyden er trukket til.
Teorem
Arealet til en konveks firkant hvis diagonaler er vinkelrette er lik halvparten av produktet av diagonalene.
Bevis
Tenk på firkanten \(ABCD\) . La oss betegne \(AO=a, CO=b, BO=x, DO=y\) :

Merk at denne firkanten består av fire rette trekanter, derfor er arealet lik summen av arealene til disse trekantene:
\(\begin(multline*) S_(ABCD)=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b) y)=\frac12(a+b)(x+y)\end(flerlinje*)\)
Konsekvens: område av en rombe
Arealet til en rombe er lik halvparten av produktet av diagonalene: \
Definisjon
Høyden på en trapes er en vinkelrett trukket fra toppen av den ene basen til den andre basen.
Teorem: Arealet av en trapes
Arealet til en trapes er lik produktet av halvparten av summen av basene og høyden.
Bevis
Tenk på trapesen \(ABCD\) med baser \(BC\) og \(AD\) . La oss tegne \(CD"\parallell AB\) som vist i figuren:

Da er \(ABCD"\) et parallellogram.
La oss også utføre \(BH"\perp AD, CH\perp AD\) (\(BH"=CH\) er høydene til trapesen).
Da \(S_(ABCD")=BH"\cdot AD"=BH"\cdot BC, \quad S_(CDD")=\dfrac12CH\cdot D"D\)
Fordi en trapes består av et parallellogram \(ABCD"\) og en trekant \(CDD"\), så er arealet lik summen av arealene til parallellogrammet og trekanten, det vil si:
\ \[=\dfrac12 CH\venstre(BC+AD"+D"D\høyre)=\dfrac12 CH\venstre(BC+AD\høyre)\]
1.1 Beregning av arealer i gammel tid
1.2 Ulike tilnærminger til å studere begrepene "areal", "polygon", "polygonområde"
1.2.1 Områdebegrepet. Områdeegenskaper
1.2.2 Begrepet polygon
1.2.3 Konseptet med arealet til en polygon. Beskrivende definisjon
1.3 Ulike formler for arealene til polygoner
1.4 Utledning av formler for arealene til polygoner
1.4.1 Arealet av en trekant. Herons formel
1.4.2 Arealet av et rektangel
1.4.3 Arealet av en trapes
1.4.4 Arealet av en firkant
1.4.5 Universell formel
1.4.6 Areal av n-gon
1.4.7 Beregne arealet til en polygon fra koordinatene til toppunktene
1.4.8 Picks formel
1.5 Pythagoras teorem om summen av arealene av kvadrater bygget på bena til en rettvinklet trekant
1.6 Like arrangement av trekanter. Bolyay-Gerwin teorem
1,7 Arealforhold lignende trekanter
1.8 Figurer med størst areal
1.8.1 Trapes eller rektangel
1.8.2 Bemerkelsesverdig egenskap ved torget
1.8.3 Seksjoner av andre former
1.8.4 Trekant med størst areal
Kapittel 2. Metodiske trekk ved å studere arealene til polygoner i matematikktimer
2.1 Tematisk planlegging og trekk ved undervisning i klasser med fordypning i matematikk
2.2 Metodikk for gjennomføring av undervisning
2.3 Resultater av forsøksarbeid
Konklusjon
Litteratur
Introduksjon
Emnet "Area of Polygons" er en integrert del av skolematematikkkurset, noe som er ganske naturlig. Tross alt er selve fremveksten av geometri historisk sett forbundet med behovet for å sammenligne tomter av en eller annen form. Imidlertid bør det bemerkes at utdanningsmuligheter for å dekke dette emnet i videregående skole er langt fra fullt brukt.
Hovedoppgaven med undervisning i matematikk på skolen er å sikre elevenes sterke og bevisste mestring av systemet med matematisk kunnskap og ferdigheter som kreves i hverdagen og arbeidsaktivitet for hvert medlem moderne samfunn tilstrekkelig for å studere relaterte disipliner og etterutdanning.
Sammen med å løse hovedproblemet, involverer dybdestudier av matematikk dannelsen hos studenter av en bærekraftig interesse for faget, identifisere og utvikle deres matematiske evner, orientering mot yrker som er vesentlig relatert til matematikk, forberedelse til å studere ved et universitet.
Kvalifiseringsarbeid inkluderer innhold i matematikkkurs ungdomsskolen og en rekke tilleggsspørsmål i direkte tilknytning til dette kurset og utdyper det langs de ideologiske hovedlinjene.
Inkluderingen av tilleggsspørsmål har to sammenhengende formål. På den ene siden er dette opprettelsen, i forbindelse med hoveddelene av kurset, av en base for å tilfredsstille interessene og utviklingen av evnene til elever med en forkjærlighet for matematikk, på den annen side er det oppfyllelsen av innholdshullene i hovedkurset, noe som gir innholdet i fordypningen den nødvendige integriteten.
Det kvalifiserende arbeidet består av en introduksjon, to kapitler, en konklusjon og sitert litteratur. Det første kapittelet diskuterer det teoretiske grunnlaget for å studere arealene til polygoner, og det andre kapittelet tar direkte for seg de metodiske trekkene ved studiet av områder.
Kapittel 1. Teoretisk grunnlag for å studere arealene til polygoner
1.1Beregning av arealer i gammel tid
Begynnelsen av geometrisk kunnskap knyttet til måling av områder går tapt i dypet av tusenvis av år.
Selv for 4 - 5 tusen år siden var babylonerne i stand til å bestemme arealet til et rektangel og trapes i kvadratiske enheter. Plassen har lenge fungert som en standard for måling av arealer på grunn av sine mange bemerkelsesverdige egenskaper: like sider, like og rette vinkler, symmetri og generell formfullkommenhet. Firkanter er enkle å konstruere, eller du kan fylle et fly uten hull.
I det gamle Kina Arealet var et rektangel. Når murere bestemte arealet til en rektangulær vegg i et hus, multipliserte de høyden og bredden på veggen. Dette er definisjonen som er akseptert i geometri: arealet av et rektangel er lik produktet av dets tilstøtende sider. Begge disse sidene må uttrykkes i de samme lineære enhetene. Produktet deres vil være arealet av rektangelet, uttrykt i de tilsvarende kvadratiske enhetene. La oss si at hvis høyden og bredden til en vegg måles i desimeter, vil produktet av begge målingene bli uttrykt i kvadratdesimeter. Og hvis arealet til hver motstående flåte er en kvadratdesimeter, vil det resulterende produktet indikere antall fliser som trengs for kledningen. Dette følger av utsagnet som ligger til grunn for målingen av arealer: arealet til en figur sammensatt av ikke-kryssende figurer er lik summen av arealene deres.
De gamle egypterne for 4000 år siden brukte nesten de samme teknikkene som vi gjør for å måle arealet til et rektangel, trekant og trapes: trekantens base ble delt i to og multiplisert med høyden; for en trapes ble summen av de parallelle sidene delt i to og multiplisert med høyden osv. For å beregne areal
firkant med sider (fig. 1.1), formel (1.1) ble bruktde. De halve summene av de motsatte sidene ble multiplisert.
Denne formelen er helt klart feil for en hvilken som helst firkant, det følger spesielt at arealene til alle romber er de samme. I mellomtiden er det åpenbart at arealene til slike romber avhenger av størrelsen på vinklene ved toppunktene. Denne formelen gjelder bare for et rektangel. Med dens hjelp kan du omtrent beregne arealet av firkanter hvis vinkler er nær rette vinkler.
For å bestemme området
likebenet trekant (fig. 1.2), der egypterne brukte den omtrentlige formelen:(1.2) Fig. 1.2 Feilen som gjøres i dette tilfellet er mindre, jo mindre forskjellen er mellom siden og høyden på trekanten, med andre ord, jo nærmere toppunktet (og ) til bunnen av høyden fra . Det er derfor den omtrentlige formelen (1.2) bare gjelder for trekanter med en relativt liten vinkel på toppen.
Men allerede de gamle grekerne visste hvordan de skulle finne områdene med polygoner. I sine elementer bruker ikke Euklid ordet «område», siden han med selve ordet «figur» forstår en del av et plan avgrenset av en eller annen lukket linje. Euklid uttrykker ikke resultatet av å måle arealet med et tall, men sammenligner arealene til forskjellige figurer med hverandre.
I likhet med andre eldgamle forskere, tar Euklid for seg omformingen av noen figurer til andre av samme størrelse. Arealet til en sammensatt figur vil ikke endres hvis delene er arrangert annerledes, men uten å krysse hverandre. Derfor er det for eksempel mulig, basert på formlene for arealet til et rektangel, å finne formler for arealene til andre figurer. Dermed er en trekant delt inn i deler som det da kan dannes et like stort rektangel av. Fra denne konstruksjonen følger det at arealet av en trekant er lik halvparten av produktet av basen og høyden. Ved å ty til en slik rekut finner de at arealet av et parallellogram er lik produktet av basen og høyden, og arealet av en trapes er produktet av halvparten av summen av basene og høyden .
Når murere skal flislegge en vegg kompleks konfigurasjon, kan de bestemme arealet av veggen ved å telle antall fliser som brukes til å vende. Noen fliser må selvfølgelig skjæres til slik at kantene på kledningen faller sammen med kanten på veggen. Antallet av alle fliser brukt i arbeidet anslår veggarealet med et overskudd, antall ubrutte fliser – med en mangel. Når størrelsen på cellene avtar, avtar mengden avfall, og veggarealet, bestemt gjennom antall fliser, beregnes mer og mer nøyaktig.
En av de senere greske matematikerne og encyklopedistene, hvis arbeider hovedsakelig var av anvendt karakter, var Heron av Alexandria, som levde i det 1. århundre. n. e. Som en fremragende ingeniør ble han også kalt "Heron the Mechanic". I sitt arbeid "Dioptrics" beskriver Heron ulike maskiner og praktiske måleinstrumenter.
En av Herons bøker ble kalt "Geometrics" av ham og er en slags samling av formler og tilsvarende problemer. Den inneholder eksempler på beregning av arealer av kvadrater, rektangler og trekanter. Om å finne arealet til en trekant basert på sidene, skriver Heron: «La for eksempel en side av trekanten ha en lengde på 13 målesnorer, den andre 14 og den tredje 15. For å finne området, fortsett som følger. Legg til 13, 14 og 15; det vil være 42. Halvparten av dette vil være 21. Trekk fra dette de tre sidene en etter en; trekk først 13 - du sitter igjen med 8, så 14 - du sitter igjen med 7, og til slutt 15 - du sitter igjen med 6. Gang dem nå: 21 ganger 8 gir 168, ta dette 7 ganger - du får 1176, og ta dette 6 ganger til - du får 7056. Herfra vil kvadratroten være 84. Dette er hvor mange målesnorer vil være i området til trekanten.»
 Hemmelig ekspedisjon av OGPU til det mystiske landet Shambhala
Hemmelig ekspedisjon av OGPU til det mystiske landet Shambhala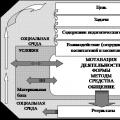 Vitenskapelig elektronisk bibliotek Den pedagogiske prosessen representerer
Vitenskapelig elektronisk bibliotek Den pedagogiske prosessen representerer Presentasjon om temaet "A.A. Blok". Presentasjon om emnet "Alexander Alexandrovich Blok" Familie og slektninger
Presentasjon om temaet "A.A. Blok". Presentasjon om emnet "Alexander Alexandrovich Blok" Familie og slektninger