Bestem spekteret til en periodisk sekvens av trekantede pulser. Elektriske og tidsmessige parametere for rektangulære pulser

La oss vurdere en periodisk sekvens av rektangulære pulser med en periode T, pulsvarighet og maksimal verdi . La oss finne serieutvidelsen til et slikt signal ved å velge opprinnelsen til koordinatene som vist i fig. 15. I dette tilfellet er funksjonen symmetrisk om ordinataksen, dvs. alle koeffisienter av sinusformede komponenter .

- 0 =0, og kun koeffisientene må beregnes

T t
(28)

konstant komponent
Den konstante komponenten er gjennomsnittsverdien over perioden, dvs. dette er området for impulsen
, delt på hele perioden, dvs.

, dvs. det samme som skjedde med en streng formell beregning (28). La oss huske at frekvensen til den første harmoniske  1 =
, hvor T er perioden for det rektangulære signalet. Avstand mellom harmoniske= 1. Hvis det harmoniske tallet n viser seg å være slik at argumentet til sinus, hvor

(29)

. Det harmoniske tallet der amplituden forsvinner for første gang kalles "første null"= og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske: på den annen side er arbeidssyklusen S av pulser forholdet mellom perioden T og pulsvarigheten t u , dvs.
.
Derfor er den "første null" numerisk lik pulsens driftssyklus N S og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske:=2 . "første null"=2 Siden sinusen går til null for alle verdiene av argumentet som er multipler av , går amplitudene til alle harmoniske med tall som er multipler av tallet til den "første null" også til null. Det vil si

på , Hvor k– et hvilket som helst heltall. Så, for eksempel, fra (22) og (23) følger det at spekteret av rektangulære pulser med en arbeidssyklus på 2 kun består av odde harmoniske. Siden og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske:=2, , Hvor k 1 , da og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske:=5, , Hvor k 1 , dvs. amplituden til den andre harmoniske går til null for første gang - dette er den "første null". Men da er amplitudene til alle andre harmoniske med tall delelig med 2, dvs. alle partall må også gå til null. og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske:=10, , Hvor k 1 =19,7V, dvs. Når arbeidssyklusen øker, avtar amplituden til den første harmoniske kraftig. , Hvor k 5 Hvis vi for eksempel finner amplitudeforholdet til den 5. harmoniske , Hvor k 1 til amplituden til den første harmoniske og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske:=2, , Hvor k 5 /, Hvor k 1 , deretter for og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske:=10, , Hvor k 5 / , Hvor k 1 = =0,2, og for

0,9, dvs. dempningshastigheten for høyere harmoniske avtar med økende driftssyklus.

Således, med økende driftssyklus, blir spekteret til en sekvens av rektangulære pulser mer ensartet.

2.5. Spektra med avtagende pulsvarighet og signalperiode. og angi det med bokstaven N, og understreker de spesielle egenskapene til denne harmoniske:= Juster driftssyklus/ T t n T t du kan enten endre pulsvarigheten Juster driftssyklus på T t=const, eller ved å endre perioden T kl

Juster driftssyklus =konst.T t La oss vurdere signalspektrene i dette tilfellet.=konst, =var. 1 =1/ Juster driftssyklus= Første harmoniske frekvens  =var.= =var. 1 = f "første null"= Juster driftssyklus/ T t konst og T t konst. T t 0 "første null" Første null  =var.= =var. 1 og ettersom pulsen forkortes

T t skifter til området for harmoniske med store tall. PåJuster driftssyklus , spekteret er diskret og, uendelig bred og med uendelig små harmoniske amplituder. =konst,=var. =var. 1 Vi vil øke perioden  =var. T  =var.= =var. 1 , deretter frekvensen til den første harmoniske og avstanden mellom spektrallinjer =konst, vil avta. Fordi =var. 1 =  =var.=1/T

, så vil spektrallinjene skifte til lavere frekvenser og "tettheten" til spekteret vil øke. Hvis , da blir signalet fra periodisk ikke-periodisk (enkeltpuls).

I dette tilfellet

, (30)

0, dvs. spekteret går fra diskret til kontinuerlig, bestående av et uendelig stort antall spektrallinjer plassert i uendelig liten avstand fra hverandre.
(31)

Dette fører til følgende regel: periodiske signaler genererer diskrete (linje)spektre, og ikke-periodiske signaler genererer kontinuerlige (kontinuerlige) spektre.(Når man går fra et diskret spektrum til et kontinuerlig spektrum, erstattes Fourier-serien med Fourier-integralet. Denne erstatningen utføres enklest hvis vi bruker representasjonen av Fourier-serien i kompleks form (16) og (17). Fourier-integralet for et kontinuerlig spektrum er skrevet ) Hvor Funksjon F j ringte spektral funksjon eller spektral tetthet, som avhenger av frekvens. Formler (30) og (31) kalles samlet Når man går fra et diskret spektrum til et kontinuerlig spektrum, erstattes Fourier-serien med Fourier-integralet. Denne erstatningen utføres enklest hvis vi bruker representasjonen av Fourier-serien i kompleks form (16) og (17). Fourier-integralet for et kontinuerlig spektrum er skrevet .

enveis Fourier-transformasjon =konst,, som er et spesialtilfelle av den mer generelle Laplace-transformasjonen og oppnås ved å erstatte den komplekse variabelen i Laplace-transformasjonen periodiske signaler genererer diskrete (linje)spektre, og ikke-periodiske signaler genererer kontinuerlige (kontinuerlige) spektre.(Når man går fra et diskret spektrum til et kontinuerlig spektrum, erstattes Fourier-serien med Fourier-integralet. Denne erstatningen utføres enklest hvis vi bruker representasjonen av Fourier-serien i kompleks form (16) og (17). Fourier-integralet for et kontinuerlig spektrum er skrevet ) r
på
-Spektralfunksjonen kan representeres som en envelope av koeffisientene til Fourier-serien, dvs. som grensen for linjespekteret til en periodisk funksjon ved, dvs.  ( ) – avhengighet av amplituden til spektrale komponenter på frekvens, og fasespektrum , dvs. . loven om endringer i fasen til spektralkomponentene til et signal avhengig av frekvens. Det kan vises periodiske signaler genererer diskrete (linje)spektre, og ikke-periodiske signaler genererer kontinuerlige (kontinuerlige) spektre.(amplitudespekteret er alltid en jevn funksjon, og fasespekteret er alltid en oddetallsfunksjon) Spektralfunksjonen for mange ikke-periodiske signaler (enkeltpulser av forskjellige former) er enklest og enklest å finne ved å bruke tabeller med originaler og bilder i Laplace-transformasjonen, som er gitt i undervisnings- og referanselitteratur. Etter å ha funnet bildet ifølge Laplace =var.(T) s

(32)

for en gitt ikke-periodisk funksjon =var.(T) , er spektralfunksjonen funnet
Så, ifølge (30), den ikke-periodiske funksjonen =var.(T) ser ut til å være en samling av et uendelig stort antall harmoniske med uendelig små amplituder

over hele frekvensområdet fra - til +, dvs. ytelse

i form av et Fourier-integral innebærer summering av udempede harmoniske oscillasjoner av et uendelig kontinuerlig spektrum av frekvenser.

beskrivelse av laboratorieoppsettet

Arbeidet utføres på "Signal Synthesizer" -blokken, hvis funksjonsdiagram er vist i fig. 16.

Blokken inneholder generatorer G1-G6 av de første seks harmoniske av signalet. Frekvensen til den første harmoniske er 10 kHz. Det harmoniske signalet fra utgangen til den n-te generatoren gjennom faseskifteren Ф n og attenuatoren An tilføres adderen. Faseskiftere setter de innledende fasene til  n harmoniske, og attenuatorer setter deres amplituder A n.

Generelt oppnås summen av seks harmoniske av signalet ved utgangen til addereren

For å korrekt vurdere muligheten for å overføre slike pulser via kommunikasjonskanaler, vil vi bestemme deres spektrale sammensetning. Et periodisk signal i form av pulser av enhver form kan utvides til en Fourier-serie i henhold til (7).

Signaler av forskjellige former brukes for overføring over luft- og kabelkommunikasjonslinjer. Valget av en eller annen form avhenger av typen av meldingene som sendes, frekvensspekteret til signalene og frekvens- og tidsparametere til signalene. Signaler som har en nær form til rektangulære pulser, er mye brukt i teknologien for overføring av diskrete meldinger.

La oss beregne spekteret, dvs. et sett med konstante amplituder og

harmoniske komponenter av periodiske rektangulære pulser (Figur 4,a) med varighet og periode. Siden signalet er en jevn funksjon av tid, forsvinner i uttrykk (3) alle jevne harmoniske komponenter ( =0), og de odde komponentene har følgende verdier:

(10)

Den konstante komponenten er lik

(11)

For et 1:1-signal (telegrafpunkter) Figur 4a:

,
. (12)

Moduler av amplitudene til spektralkomponentene til en sekvens av rektangulære pulser med en periode
er vist i fig. 4, b. Abscisseaksen viser hovedpulsrepetisjonsfrekvensen
() og frekvenser til odde harmoniske komponenter
,
osv. Spektrumskonvolutten endres i henhold til loven.

Når perioden øker sammenlignet med pulsvarigheten, øker antallet harmoniske komponenter i spektralsammensetningen til det periodiske signalet. For eksempel, for et signal med en periode (Figur 4, c), finner vi at den konstante komponenten er lik

I frekvensbåndet fra null til frekvens er det fem harmoniske komponenter (Figur 4, d), mens det kun er ett tidevann.

Med en ytterligere økning i pulsrepetisjonsperioden blir antallet harmoniske komponenter større og større. I det ekstreme tilfellet når
signalet blir en ikke-periodisk funksjon av tid, antallet av dets harmoniske komponenter i frekvensbåndet fra null til frekvens øker til uendelig; de vil være lokalisert ved uendelig nære frekvensavstander spekteret til det ikke-periodiske signalet blir kontinuerlig.

Figur 4

2.4 Spektrum av en enkelt puls

En enkelt videopuls er spesifisert (Figur 5):

Figur 5

Fourier-seriemetoden gir mulighet for en dyp og fruktbar generalisering, som gjør det mulig å oppnå spektralkarakteristikkene til ikke-periodiske signaler. For å gjøre dette, la oss mentalt supplere en enkelt puls med de samme pulsene, periodisk etter et visst tidsintervall, og få den tidligere studerte periodiske sekvensen:

La oss forestille oss en enkelt puls som summen av periodiske pulser med stor periode.

, (14)

hvor er heltall.

For periodisk oscillasjon

. (15)

For å gå tilbake til en enkelt impuls, la oss rette repetisjonsperioden til det uendelige: . I dette tilfellet er det åpenbart:

, (16)

La oss betegne

. (17)

Mengden er spektralkarakteristikken (funksjonen) til en enkelt puls (direkte Fourier-transformasjon). Det avhenger bare av den tidsmessige beskrivelsen av pulsen og er generelt komplekst:

, (18) hvor
; (19)

; (20)

Hvor
- modul av spektralfunksjonen (amplitude-frekvensrespons av pulsen);

- fasevinkel, fase-frekvenskarakteristikk for pulsen.

La oss finne for en enkelt puls ved å bruke formel (8), ved å bruke spektralfunksjonen:

Hvis, får vi:

. (21)

Det resulterende uttrykket kalles den inverse Fourier-transformasjonen.

Fourier-integralet definerer momentum som en uendelig sum av infinitesimale harmoniske komponenter plassert ved alle frekvenser.

På dette grunnlaget snakker de om et kontinuerlig (solid) spektrum som en enkelt puls har.

Den totale pulsenergien (energien som frigjøres ved den aktive motstanden Ohm) er lik

(22)

Endre rekkefølgen av integrering, får vi

Det interne integralet er spektralfunksjonen til momentum tatt med argumentet -, dvs. er en kompleks konjugert mengde:

Derfor

Kvadratmodul (produktet av to konjugerte komplekse tall er lik kvadratmodulen).

I dette tilfellet sies det konvensjonelt at pulsspekteret er tosidig, dvs. plassert i frekvensbåndet fra til.

Det gitte forholdet (23), som etablerer forbindelsen mellom pulsenergien (ved en motstand på 1 Ohm) og modulen til dens spektralfunksjon, er kjent som Parsevals likhet.

Den sier at energien i en puls er lik summen av energiene til alle komponentene i spekteret. Parsevals likhet karakteriserer en viktig egenskap ved signaler. Hvis et eller annet selektivt system sender bare deler av signalspekteret, og svekker dets andre komponenter, betyr dette at en del av signalenergien går tapt.

Siden kvadratet til modulen er en jevn funksjon av integrasjonsvariabelen, kan man ved å doble verdien av integralet introdusere integrasjon i området fra 0 til:

. (24)

I dette tilfellet sier de at pulsspekteret ligger i frekvensbåndet fra 0 til og kalles ensidig.

Integranden i (23) kalles energispekteret (spektral energitetthet) til pulsen

Den karakteriserer fordelingen av energi etter frekvens, og verdien ved frekvens er lik pulsenergien per frekvensbånd lik 1 Hz. Følgelig er pulsenergien et resultat av å integrere energispekteret til signalet over hele frekvensområdet. Med andre ord er energien lik arealet som er innelukket mellom kurven som viser energispekteret til signalet og abscisseaksen.

For å estimere energifordelingen over spekteret, bruk den relative integrerte energifordelingsfunksjonen (energikarakteristikk)

, (25)

Hvor
- pulsenergi i et gitt frekvensbånd fra 0 til, som karakteriserer brøkdelen av pulsenergi konsentrert i frekvensområdet fra 0 til.

For enkeltpulser av forskjellige former gjelder følgende lover:

Periodiske sekvenser av rektangulære pulser er mye brukt i elektronisk utstyr for ulike bruksområder. I dette tilfellet er forholdet mellom pulsvarigheten τ og oscillasjonsperioden Juster driftssyklus kan variere mye. For eksempel vibrasjoner som produserer klokkegeneratorer, som setter "tempoet" for datamaskindrift, er preget av sammenlignbare verdier av τ og Juster driftssyklus, og pulsene som brukes i radar kan være hundrevis av ganger kortere enn perioden. Holdning Juster driftssyklus/τ kalles arbeidssyklusen til pulsen, og den inverse verdien (τ/ Juster driftssyklus) - fyllfaktor.

Ris. 6. Sekvens av rektangulære pulser (a) og Fourier-seriekoeffisienter (b)

Tenk på en sekvens av rektangulære pulser med en amplitude EN, varighet τ og påfølgende med periode Juster driftssyklus(fig. 6, EN). La oss velge begynnelsen av tidstellingen som vist i figuren, det vil si slik at pulsen er symmetrisk i forhold til nullmerket, og beregne koeffisientene til Fourier-serien (1). Siden funksjonen s(T) med denne plasseringen av aksene viser seg å være jevn, alle b t er lik null, og for en t vi får:

Fourier-serien for en sekvens av rektangulære pulser har formen:

(6)

Verdiene til koeffisientene til Fourier-serien, beregnet ved hjelp av formler (5), er avbildet på spektraldiagrammet vist i fig. 6, b.

Odds en t kan assosieres med en funksjon
. Faktisk vil de være proporsjonale (med faktoren
) funksjonsverdier
med argumenter som tilsvarer harmoniske frekvenser. Dette kan sees hvis uttrykk (5) skrives om som følger:

(7)

Altså en funksjon som
er konvolutt for koeffisienter Fourierutvidelser sekvenser av rektangulære pulser (se fig. 6, b). Plassering av konvoluttnuller på frekvensaksen =var. kan finnes fra tilstanden
eller
, Hvor. Den første gangen går konvolutten til null ved frekvens =var.= 1/τ (eller ω = 2π/τ). Deretter gjentas nullpunktene i konvolutten kl =var.= 2/τ, 3/τ, osv. Disse frekvensene kan falle sammen (med heltalls driftssykluser) med frekvensene til alle spektrumharmoniske, og disse frekvenskomponentene fra Fourier-serien vil forsvinne. Hvis driftssyklusen er et heltall, perioden Juster driftssyklus nøyaktig et multiplum av pulsvarigheten. Da mellom de to nullpunktene i konvolutten vil det være spektrum harmoniske i mengden q- 1.

Tabell 1 illustrerer hvordan pulsparametere er relatert i tids- og frekvensrepresentasjoner. 2. Med økende periode Juster driftssyklus harmoniske på spektraldiagrammet kommer nærmere hverandre (spekteret blir "tykkere"). Men å endre bare perioden endrer ikke formen på amplitudespekterets konvolutt. Utviklingen av konvolutten (forskyvningen av dens nuller) avhenger av pulsvarigheten. Vist her er utviklingen av amplitudespektraldiagrammer for sekvenser av rektangulære pulser hvis pulsvarighet og perioder varierer. Ordinataksene til spektraldiagrammene viser de relative verdiene til de harmoniske amplitudene:
De beregnes ved hjelp av formlene:

(8)

Tabell 2. Oscillogrammer og spektrogrammer av sekvenser av rektangulære pulser

2.5. Spektra av kaotiske (støy)svingninger

Kaotisk oscillasjon s(T) - Dette tilfeldig prosess. Hver av implementeringene under konstante forhold gjentas ikke og er unik. I elektronikk forbindes kaotiske svingninger med støy- fluktuasjoner i strømmer og spenninger som endres tilfeldig på grunn av tilfeldig bevegelse av ladningsbærere. I denne sammenheng regnes kaotiske og støyvibrasjoner som synonyme.

Ris. 7. Blokkdiagram for måling av gjennomsnittlig kvadratstøyspenning

Støysvingninger kan beskrives i frekvensrepresentasjon: den er assosiert med en viss spektral karakteristikk, og for en tilfeldig prosess er den kontinuerlig. Det teoretiske grunnlaget for den spektrale nedbrytningen av kaotiske svingninger er presentert i. Uten å fordype oss i streng teori, vil vi forklare metodikken for eksperimentell forskning av statistiske parametere støyspenning s(T) i henhold til diagrammet vist i fig. 8.

R
er. 8. Skjema for måling av spektraltettheten til støyspenningsintensiteten

La oss hoppe over støyspenningen s(T) gjennom et filter som frigjør oscillasjonsenergi i et smalt bånd
nær frekvens =var.. Dersom vilkåret er oppfylt
<< =var. oscillasjonen ved filterutgangen vil ligne en sinusformet med en frekvens =var.. Imidlertid er amplituden og fasen til denne sinusoiden utsatt for kaotiske endringer. Med synkende filterbåndbredde
formen på utgangsoscillasjonen nærmer seg i økende grad en sinusformet. Amplituden minker, men forholdet mellom den gjennomsnittlige kvadratiske spenningen som går gjennom filteret ( ), til båndbredden
forblir begrenset og, med påfølgende reduksjoner i båndet, har en tendens til en viss grense W(=var.):

Grenseverdi W(=var.) kalles spektral intensitetstetthet behandle s(T). Den er lik den gjennomsnittlige intensiteten til de harmoniske komponentene per enhetsintervall på frekvensaksen. Ved måling W(=var.) bruk et smalbånds avstembart filter som kan stilles inn til hvilken som helst frekvens innenfor et gitt måleområde. Støyspenningen som går gjennom filteret utsettes for kvadratisk deteksjon og gjennomsnittlig (integrert). Resultatet er en gjennomsnittlig kvadrat: . Videre langs det kjente filterbåndet
kalkulere W(=var.). Full intensitet av prosessen- gjennomsnittlig kvadrat - funnet ved å integrere de spektrale komponentene til støy over alle frekvenser:

(10)

For å forberede deg til arbeid, bør du studere denne håndboken i sin helhet. Mer detaljert informasjon om emnet laboratoriearbeid finnes i kapittelet "Frekvensspektra for elektriske vibrasjoner, spektralanalyse" i boken.

Spektral representasjon av tidsfunksjoner er mye brukt i kommunikasjonsteori. For teoretiske og eksperimentelle studier av egenskapene til elektriske kretser og overføring av meldinger via kommunikasjonskanaler, brukes ulike typer signaler: harmoniske svingninger, konstante spenningsnivåer, sekvenser av rektangulære og radiopulser osv. Beregningssignaler i form av en enhetsfunksjon spiller en spesielt viktig rolle i teoretiske studier av elektriske kretser og impulsfunksjon (Dirac-funksjon). La oss bestemme spektrene til de vanligste typiske signalene.

11.1 Spektrum av en sekvens av rektangulære pulser

La det være en periodisk sekvens av rektangulære pulser med periode T, pulsvarighet t og amplitude A. Det analytiske uttrykket av funksjonen som beskriver pulsen på segmentet har formen

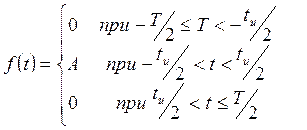(11.1)

En graf over en periodisk pulssekvens er vist i figur 11.1.

Figur 11.1

Denne funksjonen er jevn, siden grafen er symmetrisk om ordinaten. Deretter beregnes Fourier-koeffisientene til disse funksjonene ved å bruke formlene (KFT2), hvor .

Tallet representerer gjennomsnittsverdien av funksjonen over en periode og kalles konstantkomponenten. Frekvensen kalles grunntonen, eller første harmoniske, og k-frekvensene kalles høyere harmoniske, der k = 2,3,4,...

La oss konstruere amplitudespekteret til den betraktede sekvensen av rektangulære pulser. Siden funksjonen er periodisk, er dens amplitudespekter foret. La oss betegne med avstanden mellom eventuelle tilstøtende harmoniske. Det er åpenbart lik . Amplituden til den kth harmoniske i henhold til (11.2) har formen

(11.3)

La oss finne forholdet mellom perioden T og pulsvarigheten der amplituden til den k-te harmoniske blir null.

A 2 ≈32V, A 3 ≈15V, A 4 ≈0, A 5 ≈6.36V, A 6 ≈10.5V, A 7 ≈6.36V, A 8 ≈0, A 9 ≈4.95V, A 6.3.

Amplitudespekteret oppnådd som resultat av beregningen er vist i figur 11.2.

Figur 11.2

Et slikt spektrum kalles et linje- eller diskret spektrum.

Spektrene for q=8 og q=16 ble beregnet og plottet på lignende måte. De er vist i henholdsvis figur 11.3 og 11.4.

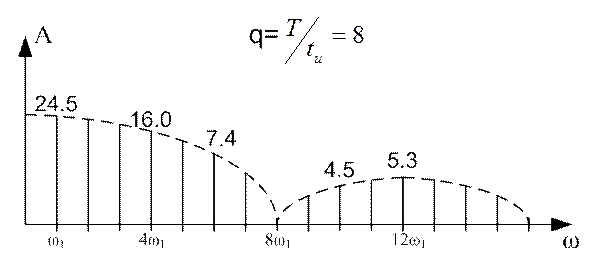
Figur 11.3

Figur 11.4

Figuren viser at jo større arbeidssyklusen til de rektangulære pulsene er, jo mindre er amplituden til den første harmoniske, men jo langsommere avtar spekteret.

11.2 Spektrum av en enkelt rektangulær puls

La oss vurdere Ф (11.1) for tilfellet når T→∞, det vil si en periodisk sekvens av pulser degenererer til en enkelt rektangulær puls med varighet t u.

Det analytiske uttrykket for denne impulsen vil bli skrevet som:

Grafen for denne funksjonen er vist i figur 11.5.

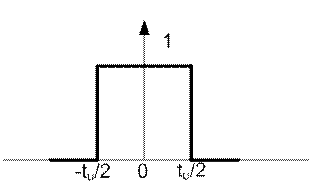
Figur 11.5

I dette tilfellet blir frekvensen til den første harmoniske og avstanden mellom harmoniske lik 0, derfor går spekteret fra diskret til kontinuerlig, bestående av et uendelig stort antall spektrallinjer plassert i uendelig liten avstand fra hverandre. Et slikt spektrum kalles kontinuerlig. Dette fører til den viktigste regelen: periodiske signaler genererer diskrete spektre, og ikke-periodiske signaler genererer kontinuerlige spektre.

Spekteret til en rektangulær enkeltpuls kan finnes direkte fra den direkte Fourier-transformasjonen (10.1)

Generelt oppnås summen av seks harmoniske av signalet ved utgangen til addereren

La oss beregne spekteret, dvs. et sett med konstante amplituder og

(10)

Den konstante komponenten er lik

(11)

For et 1:1-signal (telegrafpunkter) Figur 4a:

,
. (12)

I frekvensbåndet fra null til frekvens er det fem harmoniske komponenter (Figur 4, d), mens det kun er ett tidevann.

Figur 4

2.4 Spektrum av en enkelt puls

En enkelt videopuls er spesifisert (Figur 5):

Figur 5

La oss forestille oss en enkelt puls som summen av periodiske pulser med stor periode.

, (14)

hvor er heltall.

For periodisk oscillasjon

. (15)

For å gå tilbake til en enkelt impuls, la oss rette repetisjonsperioden til det uendelige: . I dette tilfellet er det åpenbart:

, (16)

La oss betegne

. (17)

Mengden er spektralkarakteristikken (funksjonen) til en enkelt puls (direkte Fourier-transformasjon). Det avhenger bare av den tidsmessige beskrivelsen av pulsen og er generelt komplekst:

, (18) hvor
; (19)

; (20)

Hvor
- modul av spektralfunksjonen (amplitude-frekvensrespons av pulsen);

- fasevinkel, fase-frekvenskarakteristikk for pulsen.

La oss finne for en enkelt puls ved å bruke formel (8), ved å bruke spektralfunksjonen:

Hvis, får vi:

. (21)

Det resulterende uttrykket kalles den inverse Fourier-transformasjonen.

Fourier-integralet definerer momentum som en uendelig sum av infinitesimale harmoniske komponenter plassert ved alle frekvenser.

På dette grunnlaget snakker de om et kontinuerlig (solid) spektrum som en enkelt puls har.

Den totale pulsenergien (energien som frigjøres ved den aktive motstanden Ohm) er lik

(22)

Endre rekkefølgen av integrering, får vi

Det interne integralet er spektralfunksjonen til momentum tatt med argumentet -, dvs. er en kompleks konjugert mengde:

Derfor

Kvadratmodul (produktet av to konjugerte komplekse tall er lik kvadratmodulen).

I dette tilfellet sies det konvensjonelt at pulsspekteret er tosidig, dvs. plassert i frekvensbåndet fra til.

Det gitte forholdet (23), som etablerer forbindelsen mellom pulsenergien (ved en motstand på 1 Ohm) og modulen til dens spektralfunksjon, er kjent som Parsevals likhet.

Siden kvadratet til modulen er en jevn funksjon av integrasjonsvariabelen, kan man ved å doble verdien av integralet introdusere integrasjon i området fra 0 til:

. (24)

I dette tilfellet sier de at pulsspekteret ligger i frekvensbåndet fra 0 til og kalles ensidig.

Integranden i (23) kalles energispekteret (spektral energitetthet) til pulsen

For å estimere energifordelingen over spekteret, bruk den relative integrerte energifordelingsfunksjonen (energikarakteristikk)

, (25)

Hvor
- pulsenergi i et gitt frekvensbånd fra 0 til, som karakteriserer brøkdelen av pulsenergi konsentrert i frekvensområdet fra 0 til.

For enkeltpulser av forskjellige former gjelder følgende lover: