Leksjonsoppsummering om emnet «Trigonometriske uttrykk og deres transformasjoner. Leksjon "forenkle trigonometriske uttrykk" Hvordan forenkle trigonometriske uttrykk

Videoleksjonen «Simplifying Trigonometric Expressions» er utviklet for å utvikle elevenes ferdigheter i å løse trigonometriske problemer ved å bruke grunnleggende trigonometriske identiteter. I løpet av videotimen diskuteres typer trigonometriske identiteter og eksempler på problemløsning ved bruk av dem. Ved å bruke visuelle hjelpemidler er det lettere for læreren å nå leksjonens mål. Levende presentasjon av materiale fremmer memorering viktige poeng. Bruken av animasjonseffekter og voice-over lar deg erstatte læreren fullstendig når du forklarer materialet. Ved å bruke dette visuelle hjelpemiddelet i matematikktimene kan læreren dermed øke effektiviteten av undervisningen.

I begynnelsen av videoleksjonen kunngjøres emnet. Så husker vi de trigonometriske identitetene som ble studert tidligere. Skjermen viser likhetene sin 2 t+cos 2 t=1, tg t=sin t/cos t, hvor t≠π/2+πk for kϵZ, ctg t=cos t/sin t, korrekt for t≠πk, hvor kϵZ, tg t· ctg t=1, for t≠πk/2, hvor kϵZ, kalt de grunnleggende trigonometriske identitetene. Det bemerkes at disse identitetene ofte brukes til å løse problemer der det er nødvendig å bevise likhet eller forenkle et uttrykk.

Nedenfor tar vi for oss eksempler på bruken av disse identitetene for å løse problemer. Først foreslås det å vurdere å løse problemer med å forenkle uttrykk. I eksempel 1 er det nødvendig å forenkle uttrykket cos 2 t- cos 4 t+ sin 4 t. For å løse eksempelet, ta først fellesfaktoren cos 2 t ut av parentes. Som et resultat av denne transformasjonen i parentes oppnås uttrykket 1- cos 2 t, hvis verdi fra hovedidentiteten til trigonometri er lik sin 2 t. Etter å ha transformert uttrykket er det åpenbart at en mer vanlig faktor sin 2 t kan tas ut av parentes, hvoretter uttrykket tar formen sin 2 t(sin 2 t+cos 2 t). Fra den samme grunnleggende identiteten utleder vi verdien av uttrykket i parentes lik 1. Som et resultat av forenkling får vi cos 2 t- cos 4 t+ sin 4 t= sin 2 t.

I eksempel 2 må uttrykket kostnad/(1- sint)+ kostnad/(1+ sint) forenkles. Siden tellerne til begge brøkene inneholder uttrykket kostnad, kan det tas ut av parentes som en felles faktor. Deretter reduseres brøkene i parentes til en fellesnevner ved å multiplisere (1- sint)(1+ sint). Etter å ha brakt lignende termer, forblir telleren 2, og nevneren 1 - sin 2 t. På høyre side av skjermen gjenkalles den grunnleggende trigonometriske identiteten sin 2 t+cos 2 t=1. Ved å bruke den finner vi nevneren til brøken cos 2 t. Etter å ha redusert brøken får vi en forenklet form av uttrykket kostnad/(1- sint)+ kostnad/(1+ sint)=2/kostnad.

Deretter tar vi for oss eksempler på identitetsbevis som bruker den ervervede kunnskapen om trigonometriens grunnleggende identiteter. I eksempel 3 er det nødvendig å bevise identiteten (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t. Høyre side av skjermen viser tre identiteter som vil være nødvendig for beviset - tg t·ctg t=1, ctg t=cos t/sin t og tg t=sin t/cos t med restriksjoner. For å bevise identiteten åpnes først parentesene, hvoretter det dannes et produkt som reflekterer uttrykket til den trigonometriske hovedidentiteten tg t·ctg t=1. Deretter, i henhold til identiteten fra definisjonen av cotangens, transformeres ctg 2 t. Som et resultat av transformasjonene oppnås uttrykket 1-cos 2 t. Ved hjelp av hovedidentiteten finner vi betydningen av uttrykket. Dermed er det bevist at (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t.

I eksempel 4 må du finne verdien av uttrykket tg 2 t+ctg 2 t hvis tg t+ctg t=6. For å beregne uttrykket, kvadrerer du først høyre og venstre side av likheten (tg t+ctg t) 2 =6 2. Den forkortede multiplikasjonsformelen hentes frem på høyre side av skjermen. Etter å ha åpnet parentesene på venstre side av uttrykket, dannes summen tg 2 t+2· tg t·ctg t+ctg 2 t, for å transformere som du kan bruke en av de trigonometriske identitetene tg t·ctg t=1 , hvis form er tilbakekalt på høyre side av skjermen. Etter transformasjonen oppnås likheten tg 2 t+ctg 2 t=34. Venstre side av likheten sammenfaller med problemets tilstand, så svaret er 34. Problemet er løst.

Videoleksjonen "Forenkling av trigonometriske uttrykk" anbefales for bruk i tradisjonelle skoletime matematikk. Materialet vil også være nyttig for læreren som skal implementere fjernundervisning. For å utvikle ferdigheter i å løse trigonometriske problemer.

TEKSTDEKODING:

"Forenkling av trigonometriske uttrykk."

Likheter

1) sin 2 t + cos 2 t = 1 (sinus kvadrat te pluss cosinus kvadrat te er lik én)

2)tgt =, for t ≠ + πk, kϵZ (tangens te er lik forholdet mellom sinus te og cosinus te med te ikke lik pi med to pluss pi ka, ka tilhører zet)

3)ctgt = , for t ≠ πk, kϵZ (cotangens te er lik forholdet mellom cosinus te og sinus te med te ikke lik pi ka, ka tilhører zet).

4) tgt ∙ ctgt = 1 for t ≠ , kϵZ (produktet av tangent te ved cotangens te er lik én når te ikke er lik topp ka, delt på to, ka tilhører zet)

kalles grunnleggende trigonometriske identiteter.

De brukes ofte til å forenkle og bevise trigonometriske uttrykk.

La oss se på eksempler på bruk av disse formlene for å forenkle trigonometriske uttrykk.

EKSEMPEL 1. Forenkle uttrykket: cos 2 t - cos 4 t + sin 4 t. (uttrykk a cosinus kvadrert te minus cosinus av fjerde grad te pluss sinus av fjerde grad te).

Løsning. cos 2 t - cos 4 t + sin 4 t = cos 2 t∙ (1 - cos 2 t) + sin 4 t =cos 2 t ∙ sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2 t) = sin 2 t 1= sin 2 t

(vi tar ut fellesfaktoren cosinus kvadrat te, i parentes får vi differansen mellom enhet og kvadratisk cosinus te, som er lik kvadratet sinus te ved første identitet. Vi får summen av fjerde potens sinus te av produkt cosinus kvadrat te og sinus kvadrat te. Vi tar ut fellesfaktoren sinus kvadrat te utenfor parentesene, i parentes får vi summen av kvadratene av cosinus og sinus, som ifølge den grunnleggende trigonometriske identiteten er lik 1 Som et resultat får vi kvadratet av sinus te).

EKSEMPEL 2. Forenkle uttrykket: + .

(uttrykket be er summen av to brøker i telleren til den første cosinus te i nevneren en minus sinus te, i telleren til den andre cosinus te i nevneren til den andre pluss sinus te).

(La oss ta den felles faktoren cosinus te ut av parentes, og i parentes bringer vi den til en fellesnevner, som er produktet av én minus sinus te med én pluss sinus te.

I telleren får vi: én pluss sinus te pluss én minus sinus te, vi gir like, telleren er lik to etter å ha brakt like.

I nevneren kan du bruke den forkortede multiplikasjonsformelen (kvadraters forskjell) og få forskjellen mellom enhet og kvadratet av sinus teen, som i henhold til den grunnleggende trigonometriske identiteten

lik kvadratet av cosinus te. Etter å ha redusert med cosinus te får vi det endelige svaret: to delt på cosinus te).

La oss se på eksempler på bruk av disse formlene når du beviser trigonometriske uttrykk.

EKSEMPEL 3. Bevis identiteten (tg 2 t - sin 2 t) ∙ ctg 2 t = sin 2 t (produktet av forskjellen mellom kvadratene av tangent te og sinus te med kvadratet av cotangens te er lik kvadratet av sine te).

Bevis.

La oss forvandle venstre side av likheten:

(tg 2 t - sin 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - sin 2 t ∙ ctg 2 t = 1 - sin 2 t ∙ ctg 2 t =1 - sin 2 t ∙ = 1 - cos 2 t = sin 2 t

(La oss åpne parentesen; fra det tidligere oppnådde forholdet er det kjent at produktet av kvadratene av tangent te ved cotangens te er lik en. La oss huske at cotangens te er lik forholdet mellom cosinus te og sinus te, som betyr at kvadratet av cotangens er forholdet mellom kvadratet av cosinus te og kvadratet av sinus te.

Etter reduksjon med sinus kvadrat te får vi forskjellen mellom enhet og cosinus kvadrat te, som er lik sinus kvadrat te). Q.E.D.

EKSEMPEL 4. Finn verdien av uttrykket tg 2 t + ctg 2 t hvis tgt + ctgt = 6.

(summen av kvadratene av tangent te og cotangens te, hvis summen av tangent og cotangens er seks).

Løsning. (tgt + ctgt) 2 = 6 2

tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36

tg 2 t + 2 + ctg 2 t = 36

tg 2 t + ctg 2 t = 36-2

tg 2 t + ctg 2 t = 34

La oss kvadre begge sider av den opprinnelige likheten:

(tgt + ctgt) 2 = 6 2 (kvadraten av summen av tangent te og cotangens te er lik seks i andre). La oss huske formelen for forkortet multiplikasjon: Kvadraten av summen av to mengder er lik kvadratet av den første pluss to ganger produktet av den første med den andre pluss kvadratet av den andre. (a+b) 2 =a 2 +2ab+b 2 Vi får tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 (tangens kvadrert te pluss doble produktet av tangent te ved cotangens te pluss cotangens squared te lik trettiseks) .

Siden produktet av tangent te og cotangens te er lik én, så er tg 2 t + 2 + ctg 2 t = 36 (summen av kvadratene av tangent te og cotangens te og to er lik trettiseks),

I identitetstransformasjoner trigonometriske uttrykk følgende algebraiske teknikker kan brukes: addere og subtrahere identiske termer; å sette den felles faktoren utenfor parentes; multiplikasjon og divisjon med samme mengde; anvendelse av forkortede multiplikasjonsformler; velge en komplett firkant; faktorisering av et kvadratisk trinomium; introduksjon av nye variabler for å forenkle transformasjoner.

Når du konverterer trigonometriske uttrykk som inneholder brøker, kan du bruke egenskapene proporsjon, reduserende brøk eller redusere brøk til en fellesnevner. I tillegg kan du bruke utvalget av hele delen av brøken, multiplisere telleren og nevneren til brøken med samme beløp, og også, hvis mulig, ta hensyn til homogeniteten til telleren eller nevneren. Om nødvendig kan du representere en brøk som summen eller differansen av flere enklere brøker.

I tillegg, når du bruker alle nødvendige metoder for å konvertere trigonometriske uttrykk, er det nødvendig å hele tiden ta hensyn til rekkevidden av tillatte verdier for uttrykkene som konverteres.

La oss se på noen få eksempler.

Eksempel 1.

Beregn A = (sin (2x – π) cos (3π – x) + sin (2x – 9π/2) cos (x + π/2)) 2 + (cos (x – π/2) cos (2x – 7π /2) +
+ sin (3π/2 – x) sin (2x –5π/2)) 2

Løsning.

Fra reduksjonsformlene følger det:

sin (2x – π) = -sin 2x; cos (3π – x) = -cos x;

sin (2x – 9π/2) = -cos 2x; cos (x + π/2) = -sin x;

cos (x – π/2) = sin x; cos (2x – 7π/2) = -sin 2x;

sin (3π/2 – x) = -cos x; sin (2x – 5π/2) = -cos 2x.

Hvorfra, i kraft av formlene for å legge til argumenter og den trigonometriske hovedidentiteten, får vi

A = (sin 2x cos x + cos 2x sin x) 2 + (-sin x sin 2x + cos x cos 2x) 2 = sin 2 (2x + x) + cos 2 (x + 2x) =
= sin 2 3x + cos 2 3x = 1

Svar: 1.

Eksempel 2.

Konverter uttrykket M = cos α + cos (α + β) · cos γ + cos β – sin (α + β) · sin γ + cos γ til et produkt.

Løsning.

Fra formlene for å legge til argumenter og formler for å konvertere summen av trigonometriske funksjoner til et produkt etter passende gruppering, har vi

M = (cos (α + β) cos γ – sin (α + β) sin γ) + cos α + (cos β + cos γ) =

2cos ((β + γ)/2) cos ((β – γ)/2) + (cos α + cos (α + β + γ)) =

2cos ((β + γ)/2) cos ((β – γ)/2) + 2cos (α + (β + γ)/2) cos ((β + γ)/2)) =

2cos ((β + γ)/2) (cos ((β – γ)/2) + cos (α + (β + γ)/2)) =

2cos ((β + γ)/2) 2cos ((β – γ)/2 + α + (β + γ)/2)/2) cos ((β – γ)/2) – (α + ( β + γ)/2)/2) =

4cos ((β + γ)/2) cos ((α +β)/2) cos ((α + γ)/2).

Svar: M = 4cos ((α + β)/2) · cos ((α + γ)/2) · cos ((β + γ)/2).

Eksempel 3.

Vis at uttrykket A = cos 2 (x + π/6) – cos (x + π/6) cos (x – π/6) + cos 2 (x – π/6) tar én for alle x fra R og samme betydning. Finn denne verdien.

Løsning.

Her er to måter å løse dette problemet på. Ved å bruke den første metoden, ved å isolere et komplett kvadrat og bruke de tilsvarende grunnleggende trigonometriske formlene, får vi

A = (cos (x + π/6) – cos (x – π/6)) 2 + cos (x – π/6) cos (x – π/6) =

4sin 2 x sin 2 π/6 + 1/2(cos 2x + cos π/3) =

Sin 2 x + 1/2 · cos 2x + 1/4 = 1/2 · (1 – cos 2x) + 1/2 · cos 2x + 1/4 = 3/4.

Løs problemet på den andre måten, betrakt A som en funksjon av x fra R og beregn dens deriverte. Etter transformasjoner får vi

А´ = -2cos (x + π/6) sin (x + π/6) + (sin (x + π/6) cos (x – π/6) + cos (x + π/6) sin (x + π/6)) – 2cos (x – π/6) sin (x – π/6) =

Sin 2(x + π/6) + sin ((x + π/6) + (x – π/6)) – sin 2(x – π/6) =

Sin 2x – (sin (2x + π/3) + sin (2x – π/3)) =

Sin 2x – 2sin 2x · cos π/3 = sin 2x – sin 2x ≡ 0.

Derfor, på grunn av kriteriet om konstans for en funksjon som kan differensieres på et intervall, konkluderer vi med at

A(x) ≡ (0) = cos 2 π/6 - cos 2 π/6 + cos 2 π/6 = (√3/2) 2 = 3/4, x € R.

Svar: A = 3/4 for x € R.

De viktigste teknikkene for å bevise trigonometriske identiteter er:

EN)å redusere venstre side av identiteten til høyre gjennom passende transformasjoner;
b) redusere høyre side av identiteten til venstre;
V) redusere høyre og venstre side av identiteten til samme form;
G) redusere til null forskjellen mellom venstre og høyre side av identiteten som bevises.

Eksempel 4.

Sjekk at cos 3x = -4cos x · cos (x + π/3) · cos (x + 2π/3).

Løsning.

Vi har transformert høyresiden av denne identiteten ved å bruke de tilsvarende trigonometriske formlene

4cos x cos (x + π/3) cos (x + 2π/3) =

2cos x (cos ((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) =

2cos x (cos (2x + π) + cos π/3) =

2cos x · cos 2x - cos x = (cos 3x + cos x) – cos x = cos 3x.

Høyre side av identiteten er redusert til venstre.

Eksempel 5.

Bevis at sin 2 α + sin 2 β + sin 2 γ – 2cos α · cos β · cos γ = 2, hvis α, β, γ er indre vinkler i en trekant.

Løsning.

Tatt i betraktning at α, β, γ er de indre vinklene til en trekant, får vi at

α + β + γ = π og derfor γ = π – α – β.

sin 2 α + sin 2 β + sin 2 γ – 2cos α · cos β · cos γ =

Sin 2 α + sin 2 β + sin 2 (π – α – β) – 2cos α · cos β · cos (π – α – β) =

Sin 2 α + sin 2 β + sin 2 (α + β) + (cos (α + β) + cos (α – β) · (cos (α + β) =

Sin 2 α + sin 2 β + (sin 2 (α + β) + cos 2 (α + β)) + cos (α – β) (cos (α + β) =

1/2 · (1 – cos 2α) + ½ · (1 – cos 2β) + 1 + 1/2 · (cos 2α + cos 2β) = 2.

Den opprinnelige likheten er bevist.

Eksempel 6.

Bevis at for at en av vinklene α, β, γ i trekanten skal være lik 60°, er det nødvendig og tilstrekkelig at sin 3α + sin 3β + sin 3γ = 0.

Løsning.

Tilstanden til dette problemet innebærer å bevise både nødvendighet og tilstrekkelighet.

La oss først bevise nødvendighet.

Det kan vises

sin 3α + sin 3β + sin 3γ = -4cos (3α/2) cos (3β/2) cos (3γ/2).

Ta derfor i betraktning at cos (3/2 60°) = cos 90° = 0, får vi at hvis en av vinklene α, β eller γ er lik 60°, da

cos (3α/2) cos (3β/2) cos (3γ/2) = 0 og derfor sin 3α + sin 3β + sin 3γ = 0.

La oss bevise nå tilstrekkelighet den angitte tilstanden.

Hvis sin 3α + sin 3β + sin 3γ = 0, så er cos (3α/2) cos (3β/2) cos (3γ/2) = 0, og derfor

enten cos (3α/2) = 0, eller cos (3β/2) = 0, eller cos (3γ/2) = 0.

Derfor,

eller 3α/2 = π/2 + πk, dvs. α = π/3 + 2πk/3,

eller 3β/2 = π/2 + πk, dvs. β = π/3 + 2πk/3,

eller 3γ/2 = π/2 + πk,

de. γ = π/3 + 2πk/3, hvor k ϵ Z.

Fra det faktum at α, β, γ er vinklene til en trekant, har vi

0 < α < π, 0 < β < π, 0 < γ < π.

Derfor, for α = π/3 + 2πk/3 eller β = π/3 + 2πk/3 eller

γ = π/3 + 2πk/3 av alle kϵZ er kun k = 0 egnet.

Det følger at enten α = π/3 = 60°, eller β = π/3 = 60°, eller γ = π/3 = 60°.

Utsagnet er bevist.

Har du fortsatt spørsmål? Er du usikker på hvordan du forenkler trigonometriske uttrykk?
Registrer deg for å få hjelp fra en veileder.
Den første leksjonen er gratis!

nettside, ved kopiering av materiale helt eller delvis, kreves en lenke til kilden.

Seksjoner: Matematikk

Klasse: 11

Leksjon 1

Emne: 11. klasse (forberedelse til Unified State Exam)

Forenkling av trigonometriske uttrykk.

Løse enkle trigonometriske ligninger. (2 timer)

Mål:

Systematisere, generalisere, utvide elevenes kunnskap og ferdigheter knyttet til bruk av trigonometriformler og løsning av enkle trigonometriske ligninger.

Utstyr til timen:

Leksjonsstruktur:

Organisatorisk øyeblikk
Testing på bærbare datamaskiner. Diskusjonen om resultatene.
Forenkling av trigonometriske uttrykk
Løse enkle trigonometriske ligninger
Selvstendig arbeid.
Leksjonssammendrag. Forklaring av hjemmeoppgave.

1. Organisatorisk øyeblikk. (2 minutter.)

Læreren hilser publikum, kunngjør temaet for leksjonen, minner dem om at de tidligere har fått i oppgave å gjenta trigonometriformler, og forbereder elevene til testing.

2. Testing. (15 min + 3 min diskusjon)

Målet er å teste kunnskap om trigonometriske formler og evnen til å anvende dem. Hver elev har en bærbar datamaskin på skrivebordet med en versjon av testen.

Det kan være et hvilket som helst antall alternativer, jeg vil gi et eksempel på en av dem:

jeg alternativ.

Forenkle uttrykk:

a) grunnleggende trigonometriske identiteter

1. sin 2 3y + cos 2 3y + 1;

b) addisjonsformler

3. sin5x - sin3x;

c) konvertere et produkt til en sum

6. 2sin8y cos3y;

d) doble vinkelformler

7. 2sin5x cos5x;

e) formler for halve vinkler

f) trippelvinkelformler

g) universell substitusjon

h) reduksjon i grad

16. cos 2 (3x/7);

Elevene ser svarene sine på den bærbare datamaskinen ved siden av hver formel.

Arbeidet blir umiddelbart sjekket av datamaskinen. Resultatene vises på en stor skjerm for alle å se.

Etter endt arbeid vises også de riktige svarene på elevenes bærbare datamaskiner. Hver elev ser hvor feilen ble gjort og hvilke formler han må gjenta.

3. Forenkling av trigonometriske uttrykk. (25 min.)

Målet er å gjenta, øve og konsolidere bruken av grunnleggende trigonometriformler. Løse problemer B7 fra Unified State Exam.

På sånn som det er nå Det er lurt å dele klassen inn i grupper med sterke elever (jobber selvstendig med påfølgende testing) og svake elever som jobber med læreren.

Oppgave for sterke elever (forberedt på forhånd på trykt basis). Hovedvekten er på formlene for reduksjon og dobbel vinkel, ifølge Unified State Exam 2011.

Forenkle uttrykk (for sterke elever):

Samtidig jobber læreren med svake elever, diskuterer og løser oppgaver på skjermen under elevenes diktat.

Regne ut:

5) sin(270º - α) + cos (270º + α)

Forenkle:

Det var på tide å diskutere resultatene av arbeidet til den sterke gruppen.

Svarene vises på skjermen, og også, ved hjelp av et videokamera, vises arbeidet til 5 forskjellige elever (en oppgave for hver).

Den svake gruppen ser tilstanden og løsningsmetoden. Diskusjon og analyse er i gang. Ved hjelp av tekniske midler det skjer raskt.

4. Løse enkle trigonometriske ligninger. (30 min.)

Målet er å gjenta, systematisere og generalisere løsningen av de enkleste trigonometriske ligningene og skrive ned røttene deres. Løsning av oppgave B3.

Enhver trigonometrisk ligning, uansett hvordan vi løser den, fører til den enkleste.

Når de fullfører oppgaven, bør elevene være oppmerksomme på å skrive ned røttene til ligninger av spesielle tilfeller og generelt syn og på valg av røtter i den siste ligningen.

Løs ligninger:

Skriv ned den minste positive roten som svar.

5. Selvstendig arbeid (10 min.)

Målet er å teste ferdighetene, identifisere problemer, feil og måter å eliminere dem på.

Arbeid på flere nivåer tilbys etter studentens valg.

Alternativ "3"

1) Finn verdien av uttrykket

2) Forenkle uttrykket 1 - sin 2 3α - cos 2 3α

3) Løs ligningen

Alternativ for "4"

1) Finn verdien av uttrykket

2) Løs ligningen Skriv ned den minste positive roten i svaret ditt.

Alternativ "5"

1) Finn tanα if

2) Finn roten til ligningen Skriv ned den minste positive roten som svar.

6. Leksjonssammendrag (5 min.)

Læreren oppsummerer det som ble gjentatt og forsterket i timen trigonometriske formler, løse enkle trigonometriske ligninger.

Lekser tildeles (utarbeidet på trykt basis på forhånd) med stikkprøvekontroll ved neste leksjon.

Løs ligninger:

10) I svaret ditt angir du den minste positive roten.

Leksjon 2

Emne: 11. klasse (forberedelse til Unified State Exam)

Metoder for å løse trigonometriske ligninger. Rotvalg. (2 timer)

Mål:

Generalisere og systematisere kunnskap om løsning av trigonometriske ligninger av ulike typer.
Å fremme utviklingen av elevenes matematiske tenkning, evnen til å observere, sammenligne, generalisere og klassifisere.
Oppmuntre elevene til å overvinne vanskeligheter i prosessen med mental aktivitet, til selvkontroll og introspeksjon av deres aktiviteter.

Utstyr til timen: KRMu, bærbare datamaskiner for hver student.

Leksjonsstruktur:

Organisatorisk øyeblikk
Diskusjon av d/z og selv. arbeid fra forrige leksjon
Gjennomgang av metoder for å løse trigonometriske ligninger.
Løse trigonometriske ligninger
Utvalg av røtter i trigonometriske ligninger.
Selvstendig arbeid.
Leksjonssammendrag. Hjemmelekser.

1. Organisasjonsøyeblikk (2 min.)

Læreren hilser på publikum, annonserer emnet for timen og arbeidsplanen.

2. a) Analyse hjemmelekser(5 minutter.)

Målet er å sjekke utførelse. Ett arbeid vises på skjermen ved hjelp av et videokamera, resten er selektivt samlet inn for lærerkontroll.

b) Analyse selvstendig arbeid(3 min.)

Målet er å analysere feil og angi måter å overvinne dem på.

Svar og løsninger er på skjermen, elevene har arbeidet sitt gitt ut på forhånd. Analysen går raskt.

3. Gjennomgang av metoder for å løse trigonometriske ligninger (5 min.)

Målet er å huske metoder for å løse trigonometriske ligninger.

Spør elevene hvilke metoder for å løse trigonometriske ligninger de kjenner. Understrek at det finnes såkalte grunnleggende (ofte brukte) metoder:

variabel utskifting,
faktorisering,
homogene ligninger,

og det er anvendte metoder:

bruke formlene for å konvertere en sum til et produkt og et produkt til en sum,
i henhold til formlene for å redusere graden,
universell trigonometrisk substitusjon
introduksjon av en hjelpevinkel,
multiplikasjon med noen trigonometrisk funksjon.

Det bør også huskes at en ligning kan løses på forskjellige måter.

4. Løse trigonometriske ligninger (30 min.)

Målet er å generalisere og konsolidere kunnskap og ferdigheter om dette emnet, for å forberede C1-løsningen fra Unified State Exam.

Jeg anser det som tilrådelig å løse ligninger for hver metode sammen med elever.

Eleven dikterer løsningen, læreren skriver den ned på nettbrettet, og hele prosessen vises på skjermen. Dette lar deg raskt og effektivt huske tidligere dekket materiale i minnet.

Løs ligninger:

1) erstatte variabelen 6cos 2 x + 5sinx - 7 = 0

2) faktorisering 3cos(x/3) + 4cos 2 (x/3) = 0

3) homogene ligninger sin 2 x + 3cos 2 x - 2sin2x = 0

4) konvertere summen til et produkt cos5x + cos7x = cos(π + 6x)

5) konvertere produktet til summen 2sinx sin2x + cos3x = 0

6) reduksjon av graden sin2x - sin 2 2x + sin 2 3x = 0,5

7) universell trigonometrisk substitusjon sinx + 5cosx + 5 = 0.

Når du løser denne ligningen, bør det bemerkes at ved å bruke denne metoden fører til en innsnevring av definisjonsområdet, siden sinus og cosinus erstattes med tg(x/2). Derfor, før du skriver ut svaret, må du sjekke om tallene fra settet π + 2πn, n Z er hester av denne ligningen.

8) introduksjon av en hjelpevinkel √3sinx + cosx - √2 = 0

9) multiplikasjon med en eller annen trigonometrisk funksjon cosx cos2x cos4x = 1/8.

5. Valg av røtter til trigonometriske ligninger (20 min.)

Siden det under forhold med hard konkurranse når de går inn på universiteter, ikke er nok å løse den første delen av eksamen alene, bør de fleste studenter ta hensyn til oppgavene i den andre delen (C1, C2, C3).

Derfor er målet med denne fasen av leksjonen å huske tidligere studert materiale og forberede seg på å løse problem C1 fra Unified State Exam 2011.

Eksistere trigonometriske ligninger, der det er nødvendig å velge røtter når du skriver ut svaret. Dette skyldes noen begrensninger, for eksempel: nevneren til brøken er ikke lik null, uttrykket under den partallsroten er ikke-negativt, uttrykket under logaritmetegnet er positivt, etc.

Slike ligninger betraktes som ligninger med økt kompleksitet og i versjon av Unified State Exam er i den andre delen, nemlig C1.

Løs ligningen:

En brøk er lik null hvis da ved bruk av enhetssirkel la oss velge røttene (se figur 1)

Bilde 1.

vi får x = π + 2πn, n Z

Svar: π + 2πn, n Z

På skjermen vises utvalget av røtter på en sirkel i et fargebilde.

Produktet er lik null når minst en av faktorene er lik null, og buen ikke mister sin betydning. Deretter

Ved hjelp av enhetssirkelen velger vi røttene (se figur 2)

Figur 2.

La oss gå til systemet:

I den første likningen av systemet gjør vi erstatningslog 2 (sinx) = y, vi får da likningen , la oss gå tilbake til systemet

ved hjelp av enhetssirkelen velger vi røttene (se figur 5),

Figur 5.

6. Selvstendig arbeid (15 min.)

Målet er å konsolidere og kontrollere assimileringen av materialet, identifisere feil og skissere måter å rette dem på.

Arbeidet tilbys i tre versjoner, utarbeidet på forhånd på trykt basis, som studentene kan velge mellom.

Du kan løse ligninger på alle måter.

Alternativ "3"

Løs ligninger:

1) 2sin 2 x + sinx - 1 = 0

2) sin2x = √3cosx

Alternativ for "4"

Løs ligninger:

1) cos2x = 11sinx - 5

2) (2sinx + √3)log 8 (cosx) = 0

Alternativ "5"

Løs ligninger:

1) 2sinx - 3cosx = 2

7. Leksjonssammendrag, lekser (5 min.)

Læreren oppsummerer leksjonen og gjør nok en gang oppmerksom på at en trigonometrisk likning kan løses på flere måter. Mest Den beste måten for å oppnå et raskt resultat, er det det som læres best av en bestemt elev.

Når du forbereder deg til eksamen, må du systematisk gjenta formler og metoder for å løse ligninger.

Lekser (på forhånd utarbeidet på trykt basis) deles ut og metodene for å løse noen ligninger kommenteres.

Løs ligninger:

1) cosx + cos5x = cos3x + cos7x

2) 5sin(x/6) - cos(x/3) + 3 = 0

3) 4sin 2 x + sin2x = 3

4) sin 2 x + sin 2 2x - sin 2 3x - sin 2 4x = 0

5) cos3x cos6x = cos4x cos7x

6) 4sinx - 6cosx = 1

7) 3sin2x + 4 cos2x = 5

8)cosx cos2x cos4x cos8x = (1/8)cos15x

9) (2sin 2 x - sinx)log 3 (2cos 2 x + cosx) = 0

10) (2cos 2 x - √3cosx)log 7 (-tgx) = 0

11)

Voronkova Olga Ivanovna

MBOU "videregående skole"

nr. 18"

Engels, Saratov-regionen.

Matematikklærer.

"Trigonometriske uttrykk og deres transformasjoner"

Introduksjon……………………………………………………………………………………………………… 3

Kapittel 1 Klassifisering av oppgaver om bruk av transformasjoner av trigonometriske uttrykk ………………………….………………………...5

1.1. Regneoppgaver verdier av trigonometriske uttrykk……….5

1.2.Oppgaver om å forenkle trigonometriske uttrykk... 7

1.3. Oppgaver for å konvertere numeriske trigonometriske uttrykk.....7

1.4 Blandede oppgaver………………………………………………………………………… 9

Kapittel 2. Metodiske aspekter ved organisering av den endelige repetisjonen av emnet “Transformasjon av trigonometriske uttrykk”…………………………………11

2.1 Tematisk repetisjon i 10. klasse………………………………………………………………...11

Test 1………………………………………………………………………………………..12

Test 2………………………………………………………………………………………..13

Test 3………………………………………………………………………………………..14

2.2 Avsluttende repetisjon i 11. klasse………………………………………………………………...15

Test 1………………………………………………………………………………………..17

Test 2………………………………………………………………………………………..17

Test 3………………………………………………………………………………………..18

Konklusjon ………………………………………………………………………………………………… 19

Liste over referanser………………………………………………………………..…….20

Introduksjon.

I dagens forhold er det viktigste spørsmålet: "Hvordan kan vi bidra til å eliminere noen av hullene i studentenes kunnskap og advare dem mot mulige feil på Unified State Exam?" For å løse dette problemet er det nødvendig å oppnå fra studentene ikke en formell assimilering av programmateriale, men dets dype og bevisste forståelse, utvikling av hastigheten på muntlige beregninger og transformasjoner, samt utvikling av ferdigheter i å løse enkle problemer "i sinnet." Det er nødvendig å overbevise elevene om at bare hvis det er det aktiv stilling, når du studerer matematikk, med forbehold om tilegnelse praktiske ferdigheter, ferdigheter og bruken av dem, kan du stole på reell suksess. Det er nødvendig å bruke enhver mulighet til å forberede seg til Unified State Exam, inkludert valgfag i klasse 10-11, og regelmessig gjennomgå komplekse oppgaver med studenter, velge den mest rasjonelle måten å løse dem på i leksjoner og tilleggsklasser.Positivt resultat iområder for å løse standard problemer kan oppnås hvis matematikklærere, ved å skapegod grunnleggende opplæring av studenter, se etter nye måter å løse problemene som har åpnet seg for oss, aktivt eksperimentere, bruke moderne pedagogiske teknologier, metoder, teknikker som skaper gunstige forhold for effektiv selvrealisering og selvbestemmelse av elever i nye sosiale forhold.

Trigonometri er en integrert del av skolematematikkkurset. Gode kunnskaper og sterke ferdigheter i trigonometri er bevis på et tilstrekkelig nivå av matematisk kultur, en uunnværlig betingelse vellykket studie av matematikk, fysikk og en rekke tekniske disipliner.

Arbeidets relevans. En betydelig andel av nyutdannede viser fra år til år svært dårlige forberedelser i denne viktige delen av matematikken, noe som fremgår av resultatene fra de siste årene (prosent av fullføring i 2011 - 48,41%, 2012 - 51,05%), siden analysen av bestått Unified State-eksamenen viste at studenter gjør mange feil når de fullfører oppgaver i denne seksjonen eller ikke tar på seg slike oppgaver i det hele tatt. I en På statsprøven finnes spørsmål om trigonometri i nesten tre typer oppgaver. Dette inkluderer løsningen av de enkleste trigonometriske ligningene i oppgave B5, og arbeid med trigonometriske uttrykk i oppgave B7, og studiet av trigonometriske funksjoner i oppgave B14, samt oppgavene B12, der det er formler som beskriver fysiske fenomener og inneholder trigonometriske funksjoner. Og dette er bare en del av oppgavene B! Men det er også favoritt trigonometriske ligninger med utvalg av C1 røtter, og "ikke så favoritt" geometriske oppgaver C2 og C4.

Målet med arbeidet. Analysere Unified State eksamensmateriale oppgaver B7, viet transformasjoner av trigonometriske uttrykk og klassifisere oppgaver i henhold til formen for deres presentasjon i tester.

Arbeidet består av to kapitler, innledning og avslutning. Innledningen understreker arbeidets relevans. Det første kapittelet gir en klassifisering av oppgaver for å bruke transformasjoner av trigonometriske uttrykk til testoppgaver Unified State Exam (2012).

Det andre kapittelet diskuterer organiseringen av repetisjon av emnet "Transformasjon av trigonometriske uttrykk" i klasse 10 og 11 og tester om dette emnet utvikles.

Referanselisten inkluderer 17 kilder.

Kapittel 1. Klassifisering av oppgaver ved hjelp av transformasjoner av trigonometriske uttrykk.

I samsvar med standarden for videregående (fullstendig) utdanning og kravene til forberedelsesnivået til elever, inkluderer kravkodifisereren oppgaver om kunnskap om det grunnleggende om trigonometri.

Å lære det grunnleggende om trigonometri vil være mest effektivt når:

positiv motivasjon vil bli gitt for elevene til å gjenta tidligere lært materiale;

en personorientert tilnærming vil bli implementert i utdanningsprosessen;

et system med oppgaver vil bli brukt som bidrar til å utvide, utdype og systematisere elevenes kunnskap;

Avanserte pedagogiske teknologier vil bli brukt.

Etter å ha analysert litteraturen og Internett-ressursene om forberedelse til Unified State-eksamenen, har vi foreslått en av dem mulige klassifiseringer oppgaver B7 (KIM Unified State Exam 2012-trigonometri): beregningsoppgaververdier av trigonometriske uttrykk; oppdrag forkonvertering av numeriske trigonometriske uttrykk; oppgaver for å konvertere bokstavelige trigonometriske uttrykk; blandede oppgaver.

1.1. Regneoppgaver betydningen av trigonometriske uttrykk.

En av de vanligste typene enkle trigonometriproblemer er å beregne verdiene til trigonometriske funksjoner fra verdien av en av dem:

a) Bruk av den grunnleggende trigonometriske identiteten og dens konsekvenser.

Eksempel 1 . Finn hvis
Og
.

Løsning.
,
,

Fordi , Det
.

Svar.

Eksempel 2 . Finne
, Hvis
Og .

Løsning.
,
,
.

Fordi , Det
.

Svar. .

b) Bruke dobbeltvinkelformler.

Eksempel 3 . Finne
, Hvis
.

Løsning. , .

Svar.
.

Eksempel 4 . Finn betydningen av uttrykket
.

Løsning. .

Svar.
.

1. Finne , Hvis

. Svar. -0,2

2. Finne , Hvis
Og
. Svar. 0,4

3. Finne

, Hvis . Svar. -12.884. Finne

, Hvis

. Svar. -0,845. Finn betydningen av uttrykket:

. Svar. 66. Finn betydningen av uttrykket

.Svar. -19

1.2.Oppgaver om å forenkle trigonometriske uttrykk. Reduksjonsformler bør være godt forstått av studentene, da de vil finne videre anvendelse innen geometri, fysikk og andre relaterte disipliner.

Eksempel 5 . Forenkle uttrykk
.

Løsning. .

Svar.
.

Oppgaver for selvstendig løsning:

1. Forenkle uttrykket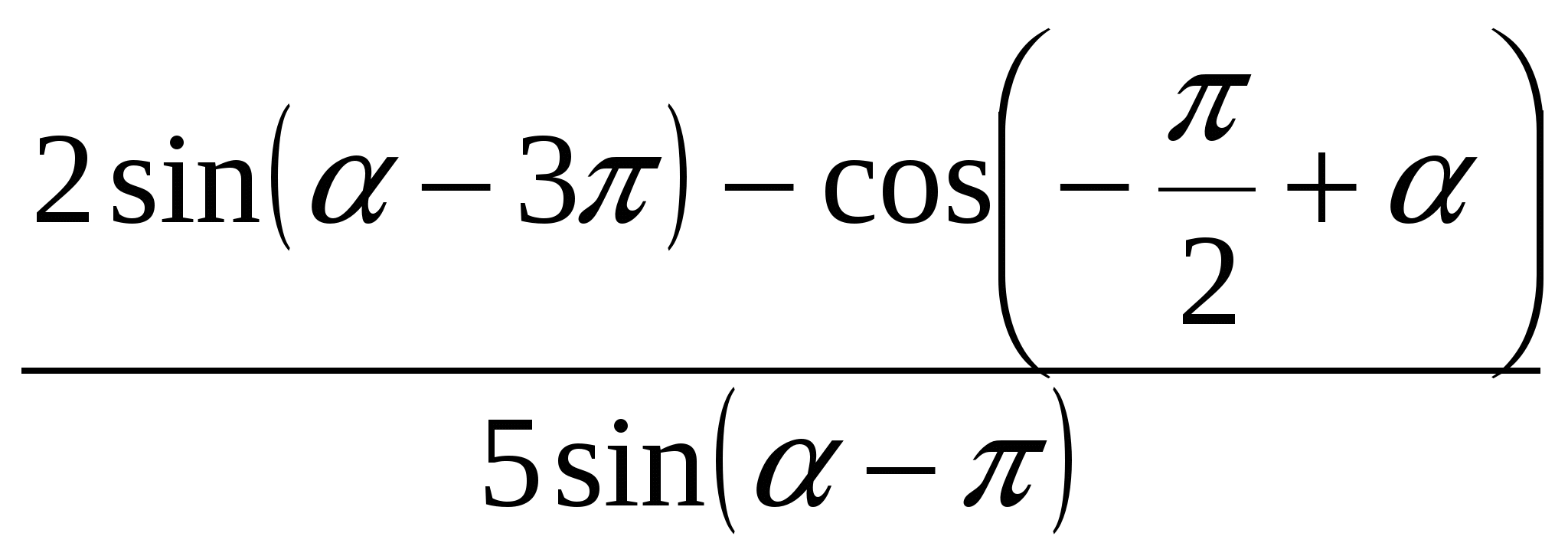

. Svar. 0,62. Finne

, Hvis

Og. Svar. 10,563. Finn betydningen av uttrykket

, Hvis

. Svar. 2

1.3. Oppgaver for å konvertere numeriske trigonometriske uttrykk.

Når du øver på ferdighetene til oppgaver for å konvertere numeriske trigonometriske uttrykk, bør du være oppmerksom på kunnskap om verditabellen for trigonometriske funksjoner, egenskapene til paritet og periodisiteten til trigonometriske funksjoner.

a) Bruke eksakte verdier av trigonometriske funksjoner for noen vinkler.

Eksempel 6 . Regne ut
.

Løsning.
.

Svar.
.

b) Bruke paritetsegenskaper trigonometriske funksjoner.

Eksempel 7 . Regne ut
.

Løsning. .

Svar.

V) Bruke periodisitetsegenskapertrigonometriske funksjoner.

Eksempel 8 . Finn betydningen av uttrykket
.

Løsning. .

Svar.
.

Oppgaver for selvstendig løsning:

1. Finn betydningen av uttrykket

. Svar. -40,52. Finn betydningen av uttrykket

. Svar. 17

3. Finn betydningen av uttrykket
. Svar. 6

. Svar. -24

Svar. -64

1.4 Blandede oppgaver.

Sertifiseringstestskjemaet har svært betydelige funksjoner, så det er viktig å være oppmerksom på oppgaver knyttet til bruk av flere trigonometriske formler samtidig.

Eksempel 9. Finne
, Hvis
.

Løsning.
.

Svar.
.

Eksempel 10 . Finne
, Hvis
Og
.

Løsning. .

Fordi , Det
.

Svar.
.

Eksempel 11. Finne
, Hvis .

Løsning. , ,
,
,
,
,
.

Svar.

Eksempel 12. Regne ut
.

Løsning. .

Svar.
.

Eksempel 13. Finn betydningen av uttrykket
, Hvis
.

Løsning. .

Svar.
.

Oppgaver for selvstendig løsning:

1. Finne

, Hvis

. Svar. -1,75
2. Finne

, Hvis

. Svar. 33. Finn

, Hvis .Svar. 0,254. Finn betydningen av uttrykket

, Hvis

. Svar. 0,35. Finn betydningen av uttrykket

, Hvis

. Svar. 5

Kapittel 2. Metodiske aspekter ved organisering av den endelige repetisjonen av emnet "Transformasjon av trigonometriske uttrykk."

En av de viktigste sakene som bidrar til ytterligere forbedring av akademiske prestasjoner og oppnåelse av dyp og varig kunnskap blant studentene, er spørsmålet om å gjenta tidligere dekket materiale. Praksis viser at i 10. klasse er det mer hensiktsmessig å organisere tematisk repetisjon; i 11. klasse - siste repetisjon.

2.1. Tematisk revisjon i 10. klasse.

I ferd med å jobbe med matematisk materiale, spesielt veldig viktig tilegner seg repetisjon av hvert fullført emne eller hele delen av kurset.

Med tematisk repetisjon systematiseres elevenes kunnskap om et emne på sluttfasen av gjennomføringen eller etter en viss pause.

For tematisk repetisjon tildeles spesielle leksjoner, der materialet til ett bestemt emne er konsentrert og generalisert.

Repetisjon i timen gjennomføres gjennom samtale med bred involvering av elevene i denne samtalen. Etter dette får elevene i oppgave å gjenta et bestemt emne og blir advart om at det vil bli utført prøvearbeid.

En test om et emne bør inneholde alle hovedspørsmålene. Etter å ha fullført arbeidet blir karakteristiske feil analysert og repetisjon organisert for å eliminere dem.

For tematiske repetisjonstimer tilbyr vi utviklet vurderingsarbeid i form av prøver om emnet "Transformasjon av trigonometriske uttrykk."

Test nr. 1

Test nr. 2

Test nr. 3

Svartabell

Test

2.2. Avsluttende anmeldelse i 11. klasse.

Endelig repetisjon utføres på sluttstadiet av å studere hovedproblemstillingene i matematikkkurset og utføres i logisk forbindelse med studiet undervisningsmateriell for denne delen eller kurset som helhet.

Den endelige repetisjonen av pedagogisk materiale forfølger følgende mål:

1. Aktivering av hele materialet treningskurså tydeliggjøre dens logiske struktur og bygge et system innenfor fag- og inter-fagforbindelser.

2. Utdype og om mulig utvide studentenes kunnskap om hovedspørsmålene i kurset i gjentakelsesprosessen.

I sammenheng med den obligatoriske beståelsen av eksamen i matematikk for alle nyutdannede, tvinger den gradvise innføringen av Unified State Exam lærere til å ta en ny tilnærming til å forberede og gjennomføre leksjoner, og ta hensyn til behovet for å sikre at alle skoleelever mestrer det pedagogiske materiale på grunnleggende nivå, samt muligheten for motiverte studenter som er interessert i å oppnå høye poengsummer for opptak til et universitet til å dynamisk avansere i å mestre materialet på et avansert og høyt nivå.

Under siste revisjonstimer kan du vurdere følgende oppgaver:

Eksempel 1 . Regn ut verdien av uttrykket.Løsning. =

= =

=0,5. Svar. 0,5. Eksempel 2. Angi den største heltallsverdien som uttrykket kan akseptere

Løsning. Fordi
kan ta hvilken som helst verdi som tilhører segmentet [–1; 1], da
tar hvilken som helst verdi av segmentet [–0,4; 0,4], derfor . Uttrykket har én heltallsverdi – tallet 4.

Svar: 4 Eksempel 3 . Forenkle uttrykket

Løsning: La oss bruke formelen for å faktorisere summen av kuber: . Vi har

Vi har:
.

Svar: 1

Eksempel 4. Regne ut
.

Løsning. .

Svar: 0,28

For siste revisjonsleksjoner tilbyr vi utviklet tester om emnet "Transformasjon av trigonometriske uttrykk."

Skriv inn det største heltall som ikke overstiger 1

Konklusjon.

Etter å ha jobbet gjennom passende metodologisk litteratur om dette emnet kan vi konkludere med at evnen og ferdighetene til å løse problemer knyttet til trigonometriske transformasjoner i skolens matematikkkurs er veldig viktig.

I løpet av det utførte arbeidet ble det foretatt en klassifisering av oppgaver B7. De trigonometriske formlene som oftest ble brukt i CMM-er i 2012 er vurdert. Det gis eksempler på oppgaver med løsninger. Det er utviklet differensierte tester for å organisere repetisjon og systematisere kunnskap som forberedelse til Unified State Exam.

Det er tilrådelig å fortsette det påbegynte arbeidet ved å vurdere løse de enkleste trigonometriske ligningene i oppgave B5, studere trigonometriske funksjoner i oppgave B14, oppgavene B12, som inneholder formler som beskriver fysiske fenomener og inneholder trigonometriske funksjoner.

Avslutningsvis vil jeg bemerke at effektiviteten bestått Unified State-eksamenen bestemmes i stor grad av hvor effektivt opplæringsprosessen er organisert på alle utdanningsnivåer, med alle kategorier av elever. Og hvis vi er i stand til å innpode elevene selvstendighet, ansvar og beredskap til å fortsette å lære gjennom hele livet, så vil vi ikke bare oppfylle statens og samfunnets orden, men også øke vår egen selvtillit.

Repetisjon av undervisningsmateriell krever lærer kreativt arbeid. Han må gi en klar sammenheng mellom repetisjonstyper og implementere et dypt gjennomtenkt system for repetisjon. Å mestre kunsten å organisere repetisjon er lærerens oppgave. Styrken til elevenes kunnskap avhenger i stor grad av løsningen.

Litteratur.

Vygodsky Ya.Ya., Håndbok i elementær matematikk. -M.: Nauka, 1970.

Problemer med økt vanskelighetsgrad i algebra og grunnleggende analyse: Lærebok for 10.-11 videregående skole/ B.M. Ivlev, A.M. Abramov, Yu.P. Dudnitsyn, S.I. Schwartzburd. – M.: Utdanning, 1990.

Anvendelse av grunnleggende trigonometriske formler til transformasjon av uttrykk (10. klasse) // Festival of Pedagogical Ideas. 2012-2013.

Koryanov A.G. , Prokofiev A.A. Vi forbereder gode og fremragende studenter til Unified State Exam. - M.: Pedagogisk universitet“Første september”, 2012.- 103 s.

Kuznetsova E.N. Forenkling av trigonometriske uttrykk. Løse trigonometriske ligninger ved hjelp av ulike metoder (forberedelse til Unified State Exam). 11. klasse. 2012-2013.

Kulanin E. D. 3000 konkurranseproblemer i matematikk. 4. utgave, riktig. og tillegg – M.: Rolf, 2000.

Mordkovich A.G. Metodiske problemer med å studere trigonometri i videregående skoler // Matematikk på skolen. 2002. Nr. 6.

Pichurin L.F. Om trigonometri og ikke bare om det: -M. Opplysning, 1985

Reshetnikov N.N. Trigonometri på skolen: -M. : Pedagogisk universitet "First of September", 2006, lx 1.

Shabunin M.I., Prokofiev A.A. Matematikk. Algebra. Begynnelsen av matematisk analyse Profilnivå: lærebok for klasse 10 - M.: BINOM. Kunnskapslaboratoriet, 2007.

Utdanningsportal for forberedelse til Unified State Exam.

Forbereder seg til Unified State-eksamenen i matematikk "Å, denne trigonometrien! http://festival.1september.ru/articles/621971/

Prosjekt "Matte? Enkelt!!!" http://www.resolventa.ru/

Seksjoner: Matematikk

Klasse: 11

Leksjon 1

Emne: 11. klasse (forberedelse til Unified State Exam)

Forenkling av trigonometriske uttrykk.

Løse enkle trigonometriske ligninger. (2 timer)

Mål:

Systematisere, generalisere, utvide elevenes kunnskap og ferdigheter knyttet til bruk av trigonometriformler og løsning av enkle trigonometriske ligninger.

Utstyr til timen:

Leksjonsstruktur:

Organisatorisk øyeblikk
Testing på bærbare datamaskiner. Diskusjonen om resultatene.
Forenkling av trigonometriske uttrykk
Løse enkle trigonometriske ligninger
Selvstendig arbeid.
Leksjonssammendrag. Forklaring av hjemmeoppgave.

1. Organisatorisk øyeblikk. (2 minutter.)

Læreren hilser publikum, kunngjør temaet for leksjonen, minner dem om at de tidligere har fått i oppgave å gjenta trigonometriformler, og forbereder elevene til testing.

2. Testing. (15 min + 3 min diskusjon)

Målet er å teste kunnskap om trigonometriske formler og evnen til å anvende dem. Hver elev har en bærbar datamaskin på skrivebordet med en versjon av testen.

Det kan være et hvilket som helst antall alternativer, jeg vil gi et eksempel på en av dem:

jeg alternativ.

Forenkle uttrykk:

a) grunnleggende trigonometriske identiteter

1. sin 2 3y + cos 2 3y + 1;

b) addisjonsformler

3. sin5x - sin3x;

c) konvertere et produkt til en sum

6. 2sin8y cos3y;

d) doble vinkelformler

7. 2sin5x cos5x;

e) formler for halve vinkler

f) trippelvinkelformler

g) universell substitusjon

h) reduksjon i grad

16. cos 2 (3x/7);

Elevene ser svarene sine på den bærbare datamaskinen ved siden av hver formel.

Arbeidet blir umiddelbart sjekket av datamaskinen. Resultatene vises på en stor skjerm for alle å se.

Etter endt arbeid vises også de riktige svarene på elevenes bærbare datamaskiner. Hver elev ser hvor feilen ble gjort og hvilke formler han må gjenta.

3. Forenkling av trigonometriske uttrykk. (25 min.)

Målet er å gjenta, øve og konsolidere bruken av grunnleggende trigonometriformler. Løse problemer B7 fra Unified State Exam.

På dette stadiet er det lurt å dele klassen inn i grupper med sterke elever (jobber selvstendig med påfølgende testing) og svake elever som jobber med læreren.

Oppgave for sterke elever (forberedt på forhånd på trykt basis). Hovedvekten er på formlene for reduksjon og dobbel vinkel, ifølge Unified State Exam 2011.

Forenkle uttrykk (for sterke elever):

Samtidig jobber læreren med svake elever, diskuterer og løser oppgaver på skjermen under elevenes diktat.

Regne ut:

5) sin(270º - α) + cos (270º + α)

Forenkle:

Det var på tide å diskutere resultatene av arbeidet til den sterke gruppen.

Svarene vises på skjermen, og også, ved hjelp av et videokamera, vises arbeidet til 5 forskjellige elever (en oppgave for hver).

Den svake gruppen ser tilstanden og løsningsmetoden. Diskusjon og analyse er i gang. Med bruk av tekniske midler skjer dette raskt.

4. Løse enkle trigonometriske ligninger. (30 min.)

Målet er å gjenta, systematisere og generalisere løsningen av de enkleste trigonometriske ligningene og skrive ned røttene deres. Løsning av oppgave B3.

Enhver trigonometrisk ligning, uansett hvordan vi løser den, fører til den enkleste.

Når du fullfører oppgaven, bør elevene være oppmerksomme på å skrive røttene til ligninger av spesielle tilfeller og generell form og til å velge røttene i den siste ligningen.

Løs ligninger:

Skriv ned den minste positive roten som svar.

5. Selvstendig arbeid (10 min.)

Målet er å teste ferdighetene, identifisere problemer, feil og måter å eliminere dem på.

Arbeid på flere nivåer tilbys etter studentens valg.

Alternativ "3"

1) Finn verdien av uttrykket

2) Forenkle uttrykket 1 - sin 2 3α - cos 2 3α

3) Løs ligningen

Alternativ for "4"

1) Finn verdien av uttrykket

2) Løs ligningen Skriv ned den minste positive roten i svaret ditt.

Alternativ "5"

1) Finn tanα if

2) Finn roten til ligningen Skriv ned den minste positive roten som svar.

6. Leksjonssammendrag (5 min.)

Læreren oppsummerer det faktum at de i løpet av leksjonen gjentok og forsterket trigonometriske formler og løste de enkleste trigonometriske ligningene.

Lekser tildeles (utarbeidet på trykt basis på forhånd) med stikkprøvekontroll ved neste leksjon.

Løs ligninger:

10) I svaret ditt angir du den minste positive roten.

Leksjon 2

Emne: 11. klasse (forberedelse til Unified State Exam)

Metoder for å løse trigonometriske ligninger. Rotvalg. (2 timer)

Mål:

Generalisere og systematisere kunnskap om løsning av trigonometriske ligninger av ulike typer.
Å fremme utviklingen av elevenes matematiske tenkning, evnen til å observere, sammenligne, generalisere og klassifisere.
Oppmuntre elevene til å overvinne vanskeligheter i prosessen med mental aktivitet, til selvkontroll og introspeksjon av deres aktiviteter.

Utstyr til timen: KRMu, bærbare datamaskiner for hver student.

Leksjonsstruktur:

Organisatorisk øyeblikk
Diskusjon av d/z og selv. arbeid fra forrige leksjon
Gjennomgang av metoder for å løse trigonometriske ligninger.
Løse trigonometriske ligninger
Utvalg av røtter i trigonometriske ligninger.
Selvstendig arbeid.
Leksjonssammendrag. Hjemmelekser.

1. Organisasjonsøyeblikk (2 min.)

Læreren hilser på publikum, annonserer emnet for timen og arbeidsplanen.

2. a) Analyse av lekser (5 min.)

Målet er å sjekke utførelse. Ett arbeid vises på skjermen ved hjelp av et videokamera, resten er selektivt samlet inn for lærerkontroll.

b) Analyse av selvstendig arbeid (3 min.)

Målet er å analysere feil og angi måter å overvinne dem på.

Svar og løsninger er på skjermen, elevene har arbeidet sitt gitt ut på forhånd. Analysen går raskt.

3. Gjennomgang av metoder for å løse trigonometriske ligninger (5 min.)

Målet er å huske metoder for å løse trigonometriske ligninger.

Spør elevene hvilke metoder for å løse trigonometriske ligninger de kjenner. Understrek at det finnes såkalte grunnleggende (ofte brukte) metoder:

variabel erstatning,
faktorisering,
homogene ligninger,

og det er anvendte metoder:

bruke formlene for å konvertere en sum til et produkt og et produkt til en sum,
i henhold til formlene for å redusere graden,
universell trigonometrisk substitusjon
introduksjon av en hjelpevinkel,
multiplikasjon med en eller annen trigonometrisk funksjon.

Det bør også huskes at en ligning kan løses på forskjellige måter.

4. Løse trigonometriske ligninger (30 min.)

Målet er å generalisere og konsolidere kunnskap og ferdigheter om dette emnet, for å forberede C1-løsningen fra Unified State Exam.

Jeg anser det som tilrådelig å løse ligninger for hver metode sammen med elever.

Eleven dikterer løsningen, læreren skriver den ned på nettbrettet, og hele prosessen vises på skjermen. Dette lar deg raskt og effektivt huske tidligere dekket materiale i minnet.

Løs ligninger:

1) erstatte variabelen 6cos 2 x + 5sinx - 7 = 0

2) faktorisering 3cos(x/3) + 4cos 2 (x/3) = 0

3) homogene ligninger sin 2 x + 3cos 2 x - 2sin2x = 0

4) konvertere summen til et produkt cos5x + cos7x = cos(π + 6x)

5) konvertere produktet til summen 2sinx sin2x + cos3x = 0

6) reduksjon av graden sin2x - sin 2 2x + sin 2 3x = 0,5

7) universell trigonometrisk substitusjon sinx + 5cosx + 5 = 0.

Ved løsning av denne ligningen bør det bemerkes at bruken av denne metoden fører til en innsnevring av definisjonsområdet, siden sinus og cosinus erstattes med tg(x/2). Derfor, før du skriver ut svaret, må du sjekke om tallene fra settet π + 2πn, n Z er hester av denne ligningen.

8) introduksjon av en hjelpevinkel √3sinx + cosx - √2 = 0

9) multiplikasjon med en eller annen trigonometrisk funksjon cosx cos2x cos4x = 1/8.

5. Valg av røtter til trigonometriske ligninger (20 min.)

Derfor er målet med denne fasen av leksjonen å huske tidligere studert materiale og forberede seg på å løse problem C1 fra Unified State Exam 2011.

Det er trigonometriske ligninger der du må velge røtter når du skriver svaret. Dette skyldes noen begrensninger, for eksempel: nevneren til brøken er ikke lik null, uttrykket under den partallsroten er ikke-negativt, uttrykket under logaritmetegnet er positivt, etc.

Slike ligninger betraktes som ligninger med økt kompleksitet og i Unified State Exam-versjonen finnes de i den andre delen, nemlig C1.

Løs ligningen:

En brøk er lik null hvis da ved å bruke enhetssirkelen velger vi røttene (se figur 1)