Hvordan finne bøyningspunkter for en funksjon. Konveksitet av funksjon
Bruksanvisning
Bøyningspunktene til en funksjon må tilhøre definisjonsdomenet, som må finnes først. Grafen til en funksjon er en linje som kan være kontinuerlig eller ha diskontinuiteter, monotont redusere eller øke, ha minimums- eller maksimumspunkter (asymptoter), være konveks eller konkav. En skarp endring i de to siste tilstandene kalles et bøyningspunkt.
En nødvendig betingelse for eksistensen av en bøyning av en funksjon er at den andre er lik null. Ved å differensiere funksjonen to ganger og likestille det resulterende uttrykket til null, kan vi således finne abscissen til mulige bøyningspunkter.
Denne tilstanden følger av definisjonen av egenskapene til konveksitet og konkavitet til grafen til en funksjon, dvs. negative og positive verdier av den andre deriverte. Ved bøyningspunktet er det en skarp endring i disse egenskapene, som betyr at den deriverte passerer nullmerket. Men å være lik null er ennå ikke nok til å indikere en bøyning.
Det er to tilstrekkelige betingelser for at abscissen som ble funnet på forrige stadium tilhører bøyningspunktet: Gjennom dette punktet kan man trekke en tangent til funksjonen. Den andre deriverte har forskjellige fortegn til høyre og venstre for det antatte bøyningspunktet. Dermed er dens eksistens på selve punktet ikke nødvendig, det er nok å bestemme at den endrer fortegn. Den andre deriverte av funksjonen er lik null, men den tredje er det ikke.
Den første tilstrekkelige tilstanden er universell og brukes oftere enn andre. Tenk på et illustrerende eksempel: y = (3 x + 3) ∛(x - 5).
Løsning: Finn definisjonsdomenet. I dette tilfellet er det ingen begrensninger, derfor er det hele plassen reelle tall. Regn ut den første deriverte: y’ = 3 ∛(x - 5) + (3 x + 3)/∛(x - 5)².
Legg merke til utseendet til brøken. Det følger av dette at definisjonsdomenet til derivatet er begrenset. Punktet x = 5 er punktert, noe som betyr at en tangent kan passere gjennom det, noe som delvis tilsvarer det første tegnet på tilstrekkelig bøyning.
Bestem de ensidige grensene for det resulterende uttrykket for x → 5 – 0 og x → 5 + 0. De er -∞ og +∞. Du har bevist at en vertikal tangent går gjennom punktet x=5. Dette punktet kan være et bøyningspunkt, men beregn først den andre deriverte: Y'' = 1/∛(x - 5)² + 3/∛(x - 5)² – 2/3 (3 x + 3)/∛ (x - 5)^5 = (2 x – 22)/∛(x - 5)^5.
Utelat nevneren siden du allerede har tatt hensyn til punktet x = 5. Løs likningen 2 x – 22 = 0. Den har en enkelt rot x = 11. Det siste trinnet er å bekrefte at punktene x = 5 og x = 11 er bøyningspunkter. Analyser oppførselen til den andre deriverte i deres nærhet. Åpenbart, ved punktet x = 5, endrer det fortegn fra "+" til "-", og ved punktet x = 11 - omvendt. Konklusjon: begge punktene er bøyningspunkter. Den første tilstrekkelige betingelsen er oppfylt.
-
-
+
+
y
-4
t r.
0



Konklusjon.
Et viktig trekk ved den vurderte metoden er at den først og fremst er basert på deteksjon og studie karakteristiske trekk i oppførselen til kurven. Steder der funksjonen endrer seg jevnt blir ikke studert i særlig detalj, og det er ikke behov for slike studier. Men de stedene der funksjonen har noen særegenheter i oppførsel er gjenstand for full forskning og de mest nøyaktige grafisk bilde. Disse funksjonene er punkter med maksimum, minimum, punkter med diskontinuitet for funksjonen, etc.
Å bestemme retningen til konkavitet og bøyninger, samt den spesifiserte metoden for å finne asymptoter, gjør det mulig å studere funksjoner enda mer detaljert og få en mer nøyaktig ide om grafene deres.
Graf av en funksjon y=f(x) kalt konveks på intervallet (a; b), hvis den er plassert under noen av tangentene i dette intervallet.
Graf av en funksjon y=f(x) kalt konkav på intervallet (a; b), hvis den er plassert over noen av tangentene i dette intervallet.
Figuren viser en kurve som er konveks kl (a; b) og konkav på (b;c).
Eksempler.

La oss vurdere tilstrekkelig indikasjon, slik at du kan bestemme om grafen til en funksjon i et gitt intervall vil være konveks eller konkav.
Teorem. La y=f(x) differensierbar på (a; b). Hvis på alle punkter av intervallet (a; b) andrederiverte av funksjonen y = f(x) negativ, dvs. f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 – konkav.
Bevis. La oss for en visshet anta det f""(x) < 0 и докажем, что график функции будет выпуклым.
La oss ta funksjonene på grafen y = f(x) vilkårlig poeng M0 med abscisse x 0 Î ( en; b) og trekk gjennom punktet M0 tangent. Hennes ligning. Vi må vise at grafen til funksjonen på (a; b) ligger under denne tangenten, dvs. til samme verdi x ordinaten til kurven y = f(x) vil være mindre enn ordinaten til tangenten.

Så ligningen til kurven er y = f(x). La oss betegne ordinaten til tangenten som tilsvarer abscissen x. Deretter . Følgelig er forskjellen mellom ordinatene til kurven og tangenten for samme verdi x vil .
Forskjell f(x) – f(x 0) transformere i henhold til Lagranges teorem, hvor c mellom x Og x 0.
Dermed,
Vi bruker igjen Lagranges teorem på uttrykket i hakeparenteser: , hvor c 1 mellom c 0 Og x 0. I henhold til betingelsene for teoremet f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Dermed ligger ethvert punkt på kurven under tangenten til kurven for alle verdier x Og x 0 Î ( en; b), som betyr at kurven er konveks. Den andre delen av teoremet er bevist på lignende måte.
Eksempler.

Punktet på grafen til en kontinuerlig funksjon som skiller dens konvekse del fra den konkave delen kalles bøyningspunkt.
Tydeligvis, ved bøyningspunktet, skjærer tangenten, hvis den eksisterer, kurven, fordi på den ene siden av dette punktet ligger kurven under tangenten, og på den andre siden - over den.

La oss bestemme tilstrekkelige betingelser for at et gitt punkt i kurven er et bøyningspunkt.
Teorem. La kurven defineres av ligningen y = f(x). Hvis f ""(x 0) = 0 eller f ""(x 0) eksisterer ikke selv når du går gjennom verdien x = x 0 derivat f ""(x) skifter fortegn, deretter punktet i grafen til funksjonen med abscissen x = x 0 det er et bøyningspunkt.
Bevis. La f ""(x) < 0 при x < x 0 Og f ""(x) > 0 kl x > x 0. Så kl x < x 0 kurven er konveks, og når x > x 0– konkav. Derfor poenget EN, liggende på kurven, med abscisse x 0 det er et bøyningspunkt. Det andre tilfellet kan vurderes på samme måte, når f ""(x) > 0 kl x < x 0 Og f ""(x) < 0 при x > x 0.

Derfor bør bøyningspunkter bare søkes blant de punktene der den andrederiverte forsvinner eller ikke eksisterer.
Eksempler. Finn bøyningspunkter og bestem intervallene for konveksitet og konkavitet for kurver.
ASYMPTOTER AV FUNKSJONENS GRAF
Når du studerer en funksjon, er det viktig å etablere formen på grafen i en ubegrenset avstand fra grafpunktet fra origo.
Av spesiell interesse er tilfellet når grafen til en funksjon, når dets variable punkt fjernes til uendelig, nærmer seg en bestemt rett linje på ubestemt tid.


Den rette linjen kalles asymptote funksjonsgrafikk y = f(x), hvis avstanden fra det variable punktet M grafikk til denne linjen når du fjerner et punkt M til det uendelige har en tendens til null, dvs. et punkt på grafen til en funksjon, ettersom det har en tendens til uendelig, må på ubestemt tid nærme seg asymptoten.
En kurve kan nærme seg sin asymptote, forbli på den ene siden av den eller på forskjellige sider, krysse asymptoten et uendelig antall ganger og bevege seg fra den ene siden til den andre.
Hvis vi betegner med d avstanden fra punktet M kurve til asymptoten, så er det klart at d har en tendens til null når punktet beveger seg bort M til det uendelige.
Vi vil videre skille mellom vertikale og skrå asymptoter.
VERTIKALE ASYMPTOTER
La kl x→ x 0 fra hvilken som helst sidefunksjon y = f(x)øker ubegrenset i absolutt verdi, dvs. eller eller ![]() . Så fra definisjonen av en asymptote følger det at den rette linjen x = x 0 er en asymptote. Det motsatte er også åpenbart, hvis linjen x = x 0 er en asymptote, dvs. .
. Så fra definisjonen av en asymptote følger det at den rette linjen x = x 0 er en asymptote. Det motsatte er også åpenbart, hvis linjen x = x 0 er en asymptote, dvs. .

Dermed den vertikale asymptoten til grafen til funksjonen y = f(x) kalles en rett linje if f(x)→ ∞ under minst én av betingelsene x→ x 0– 0 eller x → x 0 + 0, x = x 0
Derfor, for å finne de vertikale asymptotene til grafen til funksjonen y = f(x) må finne disse verdiene x = x 0, hvor funksjonen går til uendelig (lider en uendelig diskontinuitet). Da har den vertikale asymptoten ligningen x = x 0.
Eksempler.
SKÅASYMPTOTER
Siden asymptoten er en rett linje, så hvis kurven y = f(x) har en skrå asymptote, vil ligningen dens være y = kx + b. Vår oppgave er å finne koeffisientene k Og b.

Teorem. Rett y = kx + b fungerer som en skrå asymptote ved x→ +∞ for grafen til funksjonen y
= f(x) da og bare når ![]() . Et lignende utsagn gjelder for x → –∞.
. Et lignende utsagn gjelder for x → –∞.
Bevis. La MP– lengden på et segment lik avstanden fra punktet Må asymptotere. Etter betingelse. La oss betegne med φ helningsvinkelen til asymptoten til aksen Okse. Så fra ΔMNP følger det. Siden φ er en konstant vinkel (φ ≠ π/2), så , men
- Konseptet med konvekse og konkave funksjoner
Når man studerer en funksjon, kan det være nyttig å fastslå med hvilke intervaller funksjonen er konveks og med hvilke intervaller den er konkav.
For å bestemme en konveks og konkav funksjon tegner vi tangenter til grafene til funksjonen på vilkårlige punkter X 1 og X 2 (fig. 15.1 og 15.2):
Grafen til funksjonen kalles konkav på intervallet hvis det er plassert over en hvilken som helst tangent til grafen til funksjonen på dette intervallet.
Grafen til funksjonen kalles konveks på intervallet hvis det er plassert under en hvilken som helst tangent til grafen til funksjonen på dette intervallet.
Punktet i grafen til en kontinuerlig funksjon der konveksitetens natur endres kalles bøyningspunkt . Ved vendepunktet vil tangenten skjære kurven.
En funksjon kan ha flere intervaller med konveksitet og konkavitet, og flere bøyningspunkter. Når du bestemmer intervallene for konveksitet og konkavitet, velges et verdiintervall som svaret: bøyningspunkter er ikke klassifisert som verken konveksitetsintervaller eller konkavitetsintervaller.
Dermed er grafen for funksjonen i fig. 15.3 konveks på intervallene (- ; X 1) og ( X 2; + ); konkav på ( X 1 ;X 2). Grafen til funksjonen har to bøyningspunkter: ( X 1 ;på 1) og ( X 2 ;på 2).
- Kriterium for konveksitet-konkavitet til en funksjon og bøyningspunkter.
Intervallene for konveksitet og konkavitet til en funksjon er funnet ved å bruke følgende teorem:
Teorem. 1. Hvis en funksjon har en positiv andrederiverte, så er grafen til funksjonen på intervallet konkav.
2. Hvis en funksjon har en negativ andrederiverte, så er grafen til funksjonen på intervallet konveks.
La oss forestille oss kriterium for konveksitet-konkavitet til en funksjon i form av et diagram:
Å undersøke en funksjon for konveksitet-konkavitet betyr altså å finne de intervallene i definisjonsdomenet der den andre deriverte beholder sitt fortegn.
Merk at den kan endre fortegnet bare på de punktene der den andre deriverte er lik null eller ikke eksisterer. Slike punkter kalles vanligvis kritiske punkter av den andre typen .
Bare kritiske punkter kan være bøyningspunkter. For å finne dem brukes følgende teorem:
Teorem (tilstrekkelig betingelse for eksistensen av bøyningspunkter). Hvis den andre deriverte når du passerer gjennom et punkt x o skifter fortegn, deretter grafpunktet med abscissen x o er bøyningspunktet.
Når du undersøker en funksjon for konveksitet-konkavitet og bøyningspunkter, kan du bruke følgende algoritme :
Eksempel 15.1. Finn intervallene for konveksitet og konkavitet, bøyningspunktene til grafen til funksjonen.
Løsning. 1. Denne funksjonen er definert på settet R.
2. La oss finne den første deriverte av funksjonen: = .
3. Finn den andrederiverte av funksjonen: =2 X-6.
4. Definer kritiske punkter av den andre typen ( 0): 2 X-6= 0 X=3.
5. Merk det kritiske punktet på tallaksen X=3. Den deler definisjonsdomenet til funksjonen i to intervaller (-∞;3) og (3;+∞). La oss ordne tegnene til den andre deriverte av funksjon 2 X-6 ved hvert av de resulterende intervallene:
på X=0 (-∞;3) (0)=-6<0;
på X=4 (3;+∞) (4)= 2∙4-6=2>0.
|
6. I henhold til konveksitet-konkavitetskriteriet er grafen til en funksjon konveks når X(-∞;3), konkav kl X (3;+ ∞).
Betydning X=3 – abscisse av bøyningspunktet. La oss beregne verdien av funksjonen ved X=3:
2. Så, punktet med koordinater (3;2) er et bøyningspunkt.
Svar: grafen til funksjonen er konveks når X (-∞;3),
konkav kl X(3;+ ∞); (3;2) – bøyningspunkt.
Eksempel 15.2. Finn intervallene for konveksitet og konkavitet, bøyningspunktene til grafen til funksjonen.
Løsning. 1. Denne funksjonen er definert i tilfelle når nevneren ikke er null: X-7≠0 .
2. Finn den første deriverte av funksjonen:
3. La oss finne den andrederiverte av funksjonen: = =
La oss sette 2∙( X-7) utenfor parentes:
= = = . (7;+∞) (8)= >0.
|
6. I henhold til konveksitet-konkavitetskriteriet er grafen til en funksjon konveks når X(-∞;7), konkav kl X (7;+ ∞).
Abscisse prikk X=7 kan ikke være et bøyningspunkt, fordi på dette tidspunktet eksisterer ikke funksjonen (den lider av en diskontinuitet).
Svar: grafen til funksjonen er konveks når X(-∞;7), konkav kl X (7;+ ∞).
Kontrollspørsmål:
 er differensierbar på intervallet (a, b). Da er det en tangent til grafen til funksjonen når som helst
er differensierbar på intervallet (a, b). Da er det en tangent til grafen til funksjonen når som helst  dette diagrammet (
dette diagrammet (  ), og tangenten er ikke parallell med OY-aksen, siden dens vinkelkoeffisient er lik
), og tangenten er ikke parallell med OY-aksen, siden dens vinkelkoeffisient er lik  , selvfølgelig.
, selvfølgelig. besluttsomhet
besluttsomhet på (a, b) har en utløsning rettet nedover (oppover) hvis den ikke er plassert under (ikke over) noen tangent til grafen til funksjonen på (a, b).
på (a, b) har en utløsning rettet nedover (oppover) hvis den ikke er plassert under (ikke over) noen tangent til grafen til funksjonen på (a, b).  (
( ) på alle punkter i dette intervallet, så er kurven som er grafen til funksjonen konveks (konkav) på dette intervallet.
) på alle punkter i dette intervallet, så er kurven som er grafen til funksjonen konveks (konkav) på dette intervallet. kalles bøyningspunktet til grafen til en funksjon hvis den er i punktet
kalles bøyningspunktet til grafen til en funksjon hvis den er i punktet  grafen har en tangent, og det er et slikt nabolag til punktet
grafen har en tangent, og det er et slikt nabolag til punktet  , der grafen til funksjonen til venstre og høyre for punktet har forskjellige retninger av konveksitet.
, der grafen til funksjonen til venstre og høyre for punktet har forskjellige retninger av konveksitet. Det er åpenbart at tangenten ved bøyningspunktet skjærer grafen til funksjonen, siden på den ene siden av dette punktet ligger grafen over tangenten, og på den andre - under den, dvs. i nærheten av bøyningspunktet grafen for funksjonen går geometrisk fra den ene siden av tangenten til den andre og "bøyer" over den. Det er her navnet "bøyepunkt" kommer fra.
Det er åpenbart at tangenten ved bøyningspunktet skjærer grafen til funksjonen, siden på den ene siden av dette punktet ligger grafen over tangenten, og på den andre - under den, dvs. i nærheten av bøyningspunktet grafen for funksjonen går geometrisk fra den ene siden av tangenten til den andre og "bøyer" over den. Det er her navnet "bøyepunkt" kommer fra. kontinuerlig andrederiverte. Deretter
kontinuerlig andrederiverte. Deretter  .
.
 har ikke et bøyningspunkt ved (0, 0), men
har ikke et bøyningspunkt ved (0, 0), men  på
på  . Derfor er likheten til null av den andre deriverte bare
. Derfor er likheten til null av den andre deriverte bare 
 har forskjellige fortegn til venstre og høyre for punktet, så har grafen en bøyning i punktet.
har forskjellige fortegn til venstre og høyre for punktet, så har grafen en bøyning i punktet.  har en andrederiverte i et eller annet område av punktet, med unntak av selve punktet, og det er en tangent til grafen til funksjonen i punktet
har en andrederiverte i et eller annet område av punktet, med unntak av selve punktet, og det er en tangent til grafen til funksjonen i punktet  . Så, hvis den innenfor det spesifiserte nabolaget har forskjellige fortegn til venstre og til høyre for punktet, så har grafen til funksjonen en bøyning i punktet.
. Så, hvis den innenfor det spesifiserte nabolaget har forskjellige fortegn til venstre og til høyre for punktet, så har grafen til funksjonen en bøyning i punktet. 
 for konveksitet, konkavitet, bøyningspunkter.
for konveksitet, konkavitet, bøyningspunkter. 
 ,
,  =
=
 eksisterer ikke når
eksisterer ikke når 

 )
)
 )
)


 eller nær diskontinuitetspunkter av 2. type, viser det seg ofte at grafen til en funksjon nærmer seg en gitt linje så nært som ønsket. Disse kalles rette linjer.
eller nær diskontinuitetspunkter av 2. type, viser det seg ofte at grafen til en funksjon nærmer seg en gitt linje så nært som ønsket. Disse kalles rette linjer. definisjon 1.
definisjon 1. kalles en asymptote av en kurve L hvis avstanden fra et punkt på kurven til denne linjen har en tendens til null når punktet beveger seg bort langs kurven til det uendelige. Det er tre typer asymptoter: vertikal, horisontal, skrå.
kalles en asymptote av en kurve L hvis avstanden fra et punkt på kurven til denne linjen har en tendens til null når punktet beveger seg bort langs kurven til det uendelige. Det er tre typer asymptoter: vertikal, horisontal, skrå.  kalles en vertikal asymptote av grafen til en funksjon hvis minst en av de ensidige grensene er lik
kalles en vertikal asymptote av grafen til en funksjon hvis minst en av de ensidige grensene er lik  , dvs. eller
, dvs. eller 
 har en vertikal asymptote
har en vertikal asymptote  , fordi
, fordi  , A
, A  .
. Hvis
Hvis  .
.
 .
. (
( ) kalles den skrå asymptoten til grafen til funksjonen ved
) kalles den skrå asymptoten til grafen til funksjonen ved  Hvis
Hvis  ;
; 
 .
.
 ; x=0 – vertikal asymptote
; x=0 – vertikal asymptote .
.
 - skrå asymptote.
- skrå asymptote.  og plotte det.
og plotte det.  funksjonen er verken partall eller oddetall
funksjonen er verken partall eller oddetall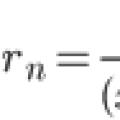 Taylor-serieutvidelse Omtrentlig løsning av Cauchy-problemet for den vanlige
Taylor-serieutvidelse Omtrentlig løsning av Cauchy-problemet for den vanlige Hva læres IKKE på skolen Hva læres ikke på skolen spør
Hva læres IKKE på skolen Hva læres ikke på skolen spør Money Thinking Formel (A
Money Thinking Formel (A