C 11 alle operasjoner med brøker. Operasjoner med brøker

496. Finne X, Hvis:

497. 1) Hvis du legger til 10 1/2 til 3/10 av et ukjent tall, får du 13 1/2. Finn det ukjente nummeret.

2) Hvis du trekker 10 1/2 fra 7/10 av et ukjent tall, får du 15 2/5. Finn det ukjente nummeret.

498 *. Hvis du trekker 10 fra 3/4 av et ukjent tall og multipliserer den resulterende forskjellen med 5, får du 100. Finn tallet.

499 *. Hvis du øker et ukjent tall med 2/3 av det, får du 60. Hvilket tall er dette?

500 *. Legger du samme beløp til det ukjente tallet, og også 20 1/3, får du 105 2/5. Finn det ukjente nummeret.

501. 1) Potetavlingen med kvadratklyngeplanting er i gjennomsnitt 150 centner per hektar, og ved konvensjonell planting er det 3/5 av denne mengden. Hvor mye mer poteter kan høstes fra et område på 15 hektar hvis poteter plantes etter kvadratklyngemetoden?

2) En erfaren arbeider produserte 18 deler på 1 time, og en uerfaren arbeider produserte 2/3 av dette beløpet. Hvor mange flere deler kan en erfaren arbeider produsere på en 7-timers dag?

502. 1) Pionerene samlet innenfor tre dager 56 kg forskjellige frø. Den første dagen ble 3/14 av den totale mengden samlet inn, den andre en og en halv gang mer, og den tredje dagen resten av kornet. Hvor mange kilo frø samlet pionerene den tredje dagen?

2) Ved maling av hveten ble resultatet: mel 4/5 av den totale mengden hvete, semulegryn - 40 ganger mindre enn mel, og resten er kli. Hvor mye mel, semulegryn og kli hver for seg ble produsert ved maling av 3 tonn hvete?

503. 1) Tre garasjer har plass til 460 biler. Antall biler som får plass i den første garasjen er 3/4 av antall biler som passer i den andre, og den tredje garasjen har 1 1/2 ganger så mange biler som den første. Hvor mange biler får plass i hver garasje?

2) En fabrikk med tre verksteder sysselsetter 6000 arbeidere. I det andre verkstedet er det 1 1/2 ganger færre arbeidere enn i det første, og antall arbeidere i det tredje verkstedet er 5/6 av antall arbeidere i det andre verkstedet. Hvor mange arbeidere er det på hvert verksted?

504. 1) Først ble 2/5, deretter 1/3 av den totale parafinen helt fra en tank med parafin, og etter det var det 8 tonn parafin igjen i tanken. Hvor mye parafin var det i tanken i utgangspunktet?

2) Syklistene kjørte i tre dager. På den første dagen dekket de 4/15 av hele reisen, på den andre - 2/5, og på den tredje dagen de resterende 100 km. Hvor langt reiste syklistene på tre dager?

505. 1) Isbryteren kjempet seg gjennom isfeltet i tre dager. Den første dagen gikk han 1/2 av hele distansen, den andre dagen 3/5 av den gjenværende distansen og den tredje dagen de resterende 24 km. Finn lengden på stien som dekkes av isbryteren på tre dager.

2) Tre grupper skoleelever plantet trær for å grønne landsbyen. Den første avdelingen plantet 7/20 av alle trærne, den andre 5/8 av de gjenværende trærne, og den tredje de resterende 195 trærne. Hvor mange trær plantet de tre lagene totalt?

506. 1) En skurtresker høstet hvete fra ett parsell på tre dager. Den første dagen høstet han fra 5/18 av hele arealet på tomten, den andre dagen fra 7/13 av det gjenværende arealet, og den tredje dagen fra det gjenværende arealet på 30 1/2 hektar. I gjennomsnitt ble det høstet 20 centners hvete fra hver hektar. Hvor mye hvete ble høstet i hele området?

2) På den første dagen dekket rallydeltakerne 3/11 av hele ruten, på den andre dagen 7/20 av den gjenværende ruten, på den tredje dagen 5/13 av den nye resten, og på den fjerde dagen de resterende 320 km. Hvor lang er ruten for rallyet?

507. 1) Den første dagen tilbakela bilen 3/8 av hele distansen, den andre dagen 15/17 av det den tilbakela den første, og den tredje dagen de resterende 200 km. Hvor mye bensin ble forbrukt hvis en bil bruker 1 3/5 kg bensin i 10 km?

2) Byen består av fire bydeler. Og 4/13 av alle innbyggerne i byen bor i det første distriktet, 5/6 av innbyggerne i det første distriktet bor i det andre, 4/11 av innbyggerne i det første bor i det tredje; to distrikter til sammen, og 18 tusen mennesker bor i det fjerde distriktet. Hvor mye brød trenger hele byens befolkning i 3 dager, hvis i gjennomsnitt én person bruker 500 g per dag?

508. 1) Turisten gikk den første dagen 31/10 av hele reisen, den andre 9/10 av det han gikk den første dagen, og den tredje resten av veien, og den tredje dagen gikk han 12 km mer enn den andre dagen. Hvor mange kilometer gikk turisten på hver av de tre dagene?

2) Bilen dekket hele ruten fra by A til by B på tre dager. Den første dagen tilbakela bilen 7/20 av hele distansen, den andre 8/13 av den gjenværende distansen, og den tredje dagen tilbakela bilen 72 km mindre enn den første dagen. Hva er avstanden mellom byer A og B?

509. 1) Forretningsutvalget tildelte jord til arbeiderne ved tre fabrikker for hageplasser. Det første anlegget ble tildelt 9/25 av det totale antall tomter, det andre anlegget 5/9 av antall tomter tildelt for det første, og det tredje - de resterende tomtene. Hvor mange tomter totalt ble tildelt arbeiderne ved tre fabrikker, dersom den første fabrikken ble tildelt 50 færre tomter enn den tredje?

2) Flyet leverte et skift med vinterarbeidere til polarstasjonen fra Moskva på tre dager. Den første dagen fløy han 2/5 av hele distansen, på den andre - 5/6 av distansen han dekket den første dagen, og den tredje dagen fløy han 500 km mindre enn den andre dagen. Hvor langt fløy flyet på tre dager?

510. 1) Anlegget hadde tre verksteder. Antall arbeidere i det første verkstedet er 2/5 av alle arbeidere i anlegget; i det andre verkstedet er det 1 1/2 ganger færre arbeidere enn i det første, og i det tredje verkstedet er det 100 flere arbeidere enn i det andre. Hvor mange arbeidere er det på fabrikken?

2) Kollektivbruket omfatter beboere i tre nabobygder. Antall familier i den første landsbyen er 3/10 av alle familier på kollektivbruket; i den andre landsbyen er antallet familier 1 1/2 ganger større enn i den første, og i den tredje landsbyen er antallet familier 420 færre enn i den andre. Hvor mange familier er det på kollektivgården?

511. 1) Artelen brukte opp 1/3 av råvarelageret den første uken, og 1/3 av resten i den andre uken. Hvor mye råstoff er det igjen i artellen hvis forbruket av råvarer den første uken var 3/5 tonn mer enn den andre uken?

2) Av det importerte kullet ble 1/6 av det brukt til oppvarming av huset den første måneden, og 3/8 av resten i den andre måneden. Hvor mye kull er det igjen for å varme opp huset hvis det ble brukt 1 3/4 mer den andre måneden enn den første måneden?

512. 3/5 av den totale jorda til kollektivbruket er avsatt til såing av korn, 13/36 av resten er okkupert av grønnsakshager og enger, resten av jorden er skog, og såarealet til kollektivbruket er 217 hektar mer område skog, 1/3 av jorda som er avsatt til kornavlinger er sådd med rug, og resten med hvete. Hvor mange hektar jord sådde kollektivbruket med hvete og hvor mange med rug?

513. 1) Trikkeveien er 14 3/8 km lang. Langs denne ruten kjører trikken 18 stopp, og bruker i gjennomsnitt opptil 1 1/6 minutt per stopp. Gjennomsnittshastigheten på trikken langs hele ruten er 12 1/2 km i timen. Hvor lang tid tar det for en trikk å fullføre én tur?

2) Bussvei 16 km. Langs denne ruten kjører bussen 36 stopp på 3/4 minutter hver. i gjennomsnitt hver. Gjennomsnittlig busshastighet er 30 km i timen. Hvor lang tid tar en buss for én rute?

514*. 1) Klokken er seks nå. kvelder. Hvilken del er den gjenværende delen av dagen fra fortiden og hvilken del av dagen er igjen?

2) En dampbåt reiser avstanden mellom to byer med strømmen på 3 dager. og tilbake samme avstand på 4 dager. Hvor mange dager vil flåtene flyte nedstrøms fra en by til en annen?

515. 1) Hvor mange plater skal brukes til å legge gulvet i et rom hvis lengde er 6 2/3 m, bredde 5 1/4 m, hvis lengden på hvert bord er 6 2/3 m og bredden er 3/ 80 av lengden?

2) En rektangulær plattform har en lengde på 45 1/2 m, og dens bredde er 5/13 av lengden. Dette området er avgrenset av en sti som er 4/5 m bred. Finn området til stien.

516. Finn gjennomsnittet aritmetiske tall:

517. 1) Det aritmetiske gjennomsnittet av to tall er 6 1/6. Et av tallene er 3 3/4. Finn et annet nummer.

2) Det aritmetiske gjennomsnittet av to tall er 14 1/4. Et av disse tallene er 15 5/6. Finn et annet nummer.

518. 1) Godstoget var på veien i tre timer. Den første timen tilbakela han 36 1/2 km, den andre 40 km og den tredje 39 3/4 km. Finn gjennomsnittshastigheten til toget.

2) Bilen kjørte 81 1/2 km de første to timene, og 95 km de neste 2 1/2 timene. Hvor mange kilometer gikk han i gjennomsnitt i timen?

519. 1) Traktorføreren fullførte oppgaven med å pløye jorden på tre dager. Den første dagen pløyde han 12 1/2 hektar, den andre dagen 15 3/4 hektar og den tredje dagen 14 1/2 hektar. Hvor mange hektar jord pløyde en traktorfører i gjennomsnitt per dag?

2) En gruppe skoleelever på en tredagers turisttur var på veien i 6 1/3 time den første dagen, 7 timer den andre. og på den tredje dagen - 4 2/3 timer. Hvor mange timer reiste skolebarn i gjennomsnitt hver dag?

520. 1) Det bor tre familier i huset. Den første familien har 3 lyspærer for å lyse opp leiligheten, den andre har 4 og den tredje har 5 lyspærer. Hvor mye skulle hver familie betale for strøm hvis alle lampene var like, og den totale strømregningen (for hele huset) var 7 1/5 rubler?

2) En polerer holdt på å polere gulvene i en leilighet der det bodde tre familier. Den første familien hadde et boareal på 36 1/2 kvadratmeter. m, den andre er 24 1/2 kvm. m, og den tredje - 43 kvm. m. For alt arbeidet ble det betalt 2 rubler. 08 kop. Hvor mye betalte hver familie?

521. 1) I hagen ble det samlet poteter fra 50 busker på 1 1/10 kg per busk, fra 70 busker på 4/5 kg per busk, fra 80 busker på 9/10 kg per busk. Hvor mange kilo poteter høstes i gjennomsnitt fra hver busk?

2) Feltmannskapet på et område på 300 hektar fikk en høst på 20 1/2 kvint høsthvete per 1 hektar, fra 80 hektar til 24 kvint per 1 ha, og fra 20 hektar - 28 1/2 kvint pr. 1 ha. Hva er gjennomsnittlig utbytte i en brigade med 1 hektar?

522. 1) Summen av to tall er 7 1/2. Det ene tallet er 4 4/5 større enn det andre. Finn disse tallene.

2) Hvis vi legger til tallene som uttrykker bredden av Tatar- og Kerchstredet sammen, får vi 11 7/10 km. Tatarstredet er 3 1/10 km bredere enn Kerchstredet. Hva er bredden på hvert sund?

523. 1) Summen av tre tall er 35 2 / 3. Det første tallet er 5 1/3 større enn det andre og 3 5/6 større enn det tredje. Finn disse tallene.

2) Øyer Ny jord, Sakhalin og Severnaya Zemlya okkuperer sammen et område på 196 7/10 tusen kvadratmeter. km. Området til Novaya Zemlya er 44 1/10 tusen kvadratmeter. km mer areal Severnaya Zemlya og 5 1/5 tusen kvm. km større enn området til Sakhalin. Hva er arealet til hver av de listede øyene?

524. 1) Leiligheten består av tre rom. Arealet til det første rommet er 24 3/8 kvm. m og er 13/36 av hele leilighetens areal. Arealet til det andre rommet er 8 1/8 kvadratmeter. m mer enn området til den tredje. Hva er arealet til det andre rommet?

2) En syklist under en tredagers konkurranse den første dagen var på veien i 3 1/4 time, som var 13/43 av den totale reisetiden. Den andre dagen syklet han 1 1/2 time mer enn den tredje dagen. Hvor mange timer reiste syklisten den andre konkurransedagen?

525. Tre jernstykker veier til sammen 17 1/4 kg. Hvis vekten av det første stykket reduseres med 1 1/2 kg, vekten av det andre med 2 1/4 kg, vil alle tre stykkene ha samme vekt. Hvor mye veide hvert jernstykke?

526. 1) Summen av to tall er 15 1/5. Hvis det første tallet reduseres med 3 1/10, og det andre økes med 3 1/10, vil disse tallene være like. Hva er hvert tall lik?

2) Det var 38 1/4 kg korn i to bokser. Heller du 4 3/4 kg frokostblanding fra en boks til en annen, vil det være like store mengder frokostblanding i begge boksene. Hvor mye frokostblanding er det i hver boks?

527 . 1) Summen av to tall er 17 17 / 30. Hvis du trekker 5 1/2 fra det første tallet og legger det til det andre, vil det første fortsatt være 2 17/30 større enn det andre. Finn begge tallene.

2) Det er 24 1/4 kg epler i to bokser. Hvis du overfører 3 1/2 kg fra den første boksen til den andre, vil det i den første fortsatt være 3/5 kg flere epler enn i den andre. Hvor mange kilo epler er det i hver boks?

528 *. 1) Summen av to tall er 8 11/14, og forskjellen deres er 2 3/7. Finn disse tallene.

2) Båten beveget seg langs elva med en hastighet på 15 1/2 km i timen, og mot strømmen med 8 1/4 km i timen. Hva er hastigheten på elvestrømmen?

529. 1) Det er 110 biler i to garasjer, og i den ene er det 1 1/5 ganger flere enn i den andre. Hvor mange biler er det i hver garasje?

2) Boarealet til en leilighet bestående av to rom er 47 1/2 kvm. m. Arealet til det ene rommet er 8/11 av arealet til det andre. Finn arealet til hvert rom.

530. 1) En legering bestående av kobber og sølv veier 330 g. Vekten av kobber i denne legeringen er 5/28 av vekten til sølv. Hvor mye sølv og hvor mye kobber er det i legeringen?

2) Summen av to tall er 6 3/4, og kvotienten er 3 1/2. Finn disse tallene.

531. Summen av tre tall er 22 1/2. Det andre tallet er 3 1/2 ganger, og det tredje er 2 1/4 ganger mer enn den første. Finn disse tallene.

532. 1) Forskjellen på to tall er 7; kvotienten for å dele et større tall med et mindre tall er 5 2/3. Finn disse tallene.

2) Forskjellen mellom to tall er 29 3/8, og deres multiplumforhold er 8 5/6. Finn disse tallene.

533. I en klasse er antall fraværende elever 3/13 av antall tilstedeværende elever. Hvor mange elever er det i klassen i følge listen hvis det er 20 flere tilstede enn fraværende?

534. 1) Forskjellen mellom to tall er 3 1/5. Ett tall er 5/7 av et annet. Finn disse tallene.

2) Faren er 24 år eldre enn sønnen. Antallet av sønnens år er lik 5/13 av farens år. Hvor gammel er faren og hvor gammel er sønnen?

535. Nevneren til en brøk er 11 enheter større enn telleren. Hva er verdien av en brøk hvis nevneren er 3 3/4 ganger telleren?

nr. 536 - 537 muntlig.

536. 1) Det første tallet er 1/2 av det andre. Hvor mange ganger er det andre tallet større enn det første?

2) Det første tallet er 3/2 av det andre. Hvilken del av det første tallet er det andre tallet?

537. 1) 1/2 av det første tallet er lik 1/3 av det andre tallet. Hvilken del av det første tallet er det andre tallet?

2) 2/3 av det første tallet er lik 3/4 av det andre tallet. Hvilken del av det første tallet er det andre tallet? Hvilken del av det andre tallet er det første?

538. 1) Summen av to tall er 16. Finn disse tallene hvis 1/3 av det andre tallet er lik 1/5 av det første.

2) Summen av to tall er 38. Finn disse tallene hvis 2/3 av det første tallet er lik 3/5 av det andre.

539 *. 1) To gutter samlet 100 sopp sammen. 3/8 av antall sopp samlet inn av den første gutten er numerisk lik 1/4 av antall sopp samlet inn av den andre gutten. Hvor mange sopp samlet hver gutt?

2) Institusjonen sysselsetter 27 personer. Hvor mange menn jobber og hvor mange kvinner jobber hvis 2/5 av alle menn er lik 3/5 av alle kvinner?

540 *. Tre gutter kjøpte en volleyball. Bestem bidraget til hver gutt, vel vitende om at 1/2 av bidraget til den første gutten er lik 1/3 av bidraget til den andre, eller 1/4 av bidraget til den tredje, og at bidraget til den tredje gutten er 64 kopek mer enn bidraget til den første.

541 *. 1) Ett tall er 6 mer enn det andre Finn disse tallene hvis 2/5 av det ene tallet er lik 2/3 av det andre.

2) Forskjellen på to tall er 35. Finn disse tallene hvis 1/3 av det første tallet er lik 3/4 av det andre tallet.

542. 1) Det første laget kan fullføre noe arbeid på 36 dager, og det andre på 45 dager. Om hvor mange dager vil begge lagene, som jobber sammen, fullføre denne jobben?

2) Et persontog dekker avstanden mellom to byer på 10 timer, og et godstog tilbakelegger denne avstanden på 15 timer. Begge togene forlot disse byene samtidig mot hverandre. Hvor mange timer vil de møtes?

543. 1) Et hurtigtog dekker avstanden mellom to byer på 6 1/4 time, og et persontog på 7 1/2 time. Hvor mange timer senere vil disse togene møtes hvis de forlater begge byene samtidig mot hverandre? (Rund svar til nærmeste 1 time.)

2) To motorsyklister dro samtidig fra to byer mot hverandre. En motorsyklist kan reise hele avstanden mellom disse byene på 6 timer, og en annen på 5 timer. Hvor mange timer etter avgang møter motorsyklistene? (Rund svar til nærmeste 1 time.)

544. 1) Tre kjøretøyer med forskjellig bærekapasitet kan transportere noe last, og arbeider separat: det første på 10 timer, det andre på 12 timer. og den tredje på 15 timer På hvor mange timer kan de frakte den samme lasten sammen?

2) To tog forlater to stasjoner samtidig mot hverandre: det første toget dekker avstanden mellom disse stasjonene på 12 1/2 time, og det andre på 18 3/4 timer. Hvor mange timer etter avgang vil togene møtes?

545. 1) To kraner er koblet til badekaret. Gjennom en av dem kan badekaret fylles på 12 minutter, gjennom den andre 1 1/2 ganger raskere. Hvor mange minutter vil det ta å fylle 5/6 av hele badekaret hvis du åpner begge kranene samtidig?

2) To maskinskrivere må skrive manuskriptet på nytt. Den første sjåføren kan fullføre dette arbeidet på 3 1/3 dager, og den andre 1 1/2 ganger raskere. Hvor mange dager vil det ta begge maskinskriverne å fullføre jobben hvis de jobber samtidig?

546. 1) Bassenget fylles med det første røret på 5 timer, og gjennom det andre røret kan det tømmes på 6 timer Etter hvor mange timer fylles hele bassenget dersom begge rørene åpnes samtidig?

Merk. I løpet av en time er bassenget fylt til (1/5 - 1/6 av kapasiteten.)

2) To traktorer pløyde åkeren på 6 timer. Den første traktoren, som jobbet alene, kunne pløye dette feltet på 15 timer Hvor mange timer ville det ta den andre traktoren, som jobbet alene, for å pløye dette feltet?

547 *. To tog går fra to stasjoner samtidig mot hverandre og møtes etter 18 timer. etter hans løslatelse. Hvor lang tid tar det andre toget å dekke avstanden mellom stasjonene hvis det første toget dekker denne avstanden på 1 dag 21 timer?

548 *. Bassenget er fylt med to rør. Først åpnet de det første røret, og så etter 3 3/4 timer, da halve bassenget var fylt, åpnet de det andre røret. Etter 2 1/2 timers arbeid sammen var bassenget fullt. Bestem kapasiteten til bassenget hvis 200 bøtter vann per time helles gjennom det andre røret.

549. 1) Et budtog forlot Leningrad til Moskva og reiser 1 km på 3/4 minutter. 1/2 time etter at dette toget forlot Moskva, forlot et hurtigtog Moskva til Leningrad, hvis hastighet var lik 3/4 av hurtigtogets hastighet. I hvilken avstand vil togene være fra hverandre 2 1/2 time etter at kurertoget går, hvis avstanden mellom Moskva og Leningrad er 650 km?

2) Fra kollektivbruket til byen 24 km. En lastebil forlater kollektivbruket og kjører 1 km på 2 1/2 minutt. Etter 15 min. Etter at denne bilen forlot byen, kjørte en syklist ut til kollektivbruket, med halvparten så høy hastighet som lastebilens hastighet. Hvor lenge etter avreise vil syklisten møte lastebilen?

550. 1) En fotgjenger kom ut fra en landsby. 4 1/2 time etter at fotgjengeren gikk, syklet en syklist i samme retning, hvis hastighet var 2 1/2 ganger farten til fotgjengeren. Hvor mange timer etter at fotgjengeren går vil syklisten forbikjøre ham?

2) Et hurtigtog kjører 187 1/2 km på 3 timer, og et godstog kjører 288 km på 6 timer. 7 1/4 time etter at godstoget går, går ambulanse i samme retning. Hvor lang tid vil det ta for hurtigtoget å komme etter godstoget?

551. 1) Fra to kollektivbruk som veien til regionsenteret går gjennom, red to kollektivbønder ut til distriktet samtidig til hest. Den første av dem reiste 8 3/4 km i timen, og den andre var 1 1/7 ganger mer enn den første. Den andre kollektivbonden tok igjen den første etter 3 4/5 timer. Bestem avstanden mellom kollektivbruk.

2) 26 1/3 time etter avgang av toget Moskva-Vladivostok, hvis gjennomsnittshastighet var 60 km i timen, lettet et TU-104-fly i samme retning, med en hastighet på 14 1/6 ganger hastigheten av toget. Hvor mange timer etter avgang vil flyet innhente toget?

552. 1) Avstanden mellom byene langs elven er 264 km. Damperen dekket denne avstanden nedstrøms på 18 timer, og brukte 1/12 av denne tiden på å stoppe. Hastigheten til elven er 1 1/2 km i timen. Hvor lang tid vil det ta et dampskip å reise 87 km uten å stoppe i stille vann?

2) En motorbåt kjørte 207 km langs elven på 13 1/2 time, og brukte 1/9 av denne tiden på stopp. Hastigheten på elven er 1 3/4 km i timen. Hvor mange kilometer kan denne båten reise i stille vann på 2 1/2 time?

553. Båten tilbakela en strekning på 52 km over reservoaret uten å stoppe på 3 timer og 15 minutter. Videre, langs elven mot strømmen, hvis hastighet er 1 3/4 km i timen, dekket denne båten 28 1/2 km på 2 1/4 time, og gjorde 3 stopp av samme varighet. Hvor mange minutter ventet båten ved hvert stopp?

554. Fra Leningrad til Kronstadt ved 12-tiden. Dampbåten dro om ettermiddagen og dekket hele avstanden mellom disse byene på 1 1/2 time. På veien møtte han et annet skip som dro fra Kronstadt til Leningrad klokken 12.18. og gå med 1 1/4 ganger hastigheten til den første. Når møttes de to skipene?

555. Toget måtte tilbakelegge en strekning på 630 km på 14 timer. Etter å ha tilbakelagt 2/3 av denne distansen ble han varetektsfengslet i 1 time og 10 minutter. Med hvilken hastighet bør han fortsette reisen for å nå målet uten forsinkelse?

556. Klokken 04:20 Om morgenen dro et godstog fra Kiev til Odessa med en gjennomsnittshastighet på 31 1/5 km i timen. Etter en tid kom et posttog ut fra Odessa for å møte ham, hvis hastighet var 1 17/39 ganger høyere enn hastigheten til et godstog, og møtte godstoget 6 1/2 time etter dets avgang. Når forlot posttoget Odessa, hvis avstanden mellom Kiev og Odessa er 663 km?

557*. Klokken viser middag. Hvor lang tid vil det ta før time- og minuttviserne faller sammen?

558. 1) Anlegget har tre verksteder. Antall arbeidere i det første verkstedet er 9/20 av alle arbeidere ved anlegget, i det andre verkstedet er det 1 1/2 ganger færre arbeidere enn i det første, og i det tredje verkstedet er det 300 færre arbeidere enn i verkstedet. sekund. Hvor mange arbeidere er det på fabrikken?

2) Det er tre ungdomsskoler i byen. Elevtallet på den første skolen er 3/10 av alle elever på disse tre skolene; på andre skole er det 1 1/2 ganger flere elever enn på første, og på tredje skole er det 420 færre elever enn på andre. Hvor mange elever er det på de tre skolene?

559. 1) To skurtreskere jobbet i samme område. Etter at den ene kombimaskinen høstet 9/16 av hele parsellen, og den andre 3/8 av samme parsell, viste det seg at den første kombimaskinen høstet 97 1/2 hektar mer enn den andre. I gjennomsnitt ble det tresket 32 1/2 kvint korn fra hver hektar. Hvor mange sentner korn tresket hver skurtresker?

2) To brødre kjøpte et kamera. Den ene hadde 5/8, og den andre 4/7 av kostnadene for kameraet, og den første hadde 2 rubler verdt. 25 kopek mer enn den andre. Alle betalte halvparten av kostnaden for enheten. Hvor mye penger har alle igjen?

560. 1) En personbil forlater by A for by B, avstanden mellom dem er 215 km, med en hastighet på 50 km i timen. Samtidig forlot en lastebil by B til by A. Hvor mange kilometer kjørte personbilen før den møtte lastebilen, hvis lastebilens hastighet i timen var 18/25 hastigheten til personbilen?

2) Mellom byer A og B 210 km. En personbil forlot by A til by B. Samtidig forlot en lastebil by B til by A. Hvor mange kilometer kjørte lastebilen før den møtte personbilen, hvis personbilen kjørte med en hastighet på 48 km i timen, og lastebilens hastighet i timen var 3/4 av personbilens hastighet?

561. Kollektivbruket høstet hvete og rug. 20 hektar mer ble sådd med hvete enn med rug. Den totale rugavlingen utgjorde 5/6 av den totale hveteavlingen med en avling på 20 c per 1 ha for både hvete og rug. Kollektivbruket solgte 7/11 av hele avlingen av hvete og rug til staten, og lot resten av kornet dekke sitt behov. Hvor mange turer måtte de to tonn tunge lastebilene kjøre for å fjerne brødet som ble solgt til staten?

562. Rug og hvetemel ble brakt til bakeriet. Vekten av hvetemel var 3/5 av vekten av rugmel, og det ble brakt 4 tonn mer rugmel enn hvetemel. Hvor mye hvete og hvor mye rugbrød vil bakeriet bake av dette melet hvis bakevarene utgjør 2/5 av det totale melet?

563. I løpet av tre dager fullførte et team av arbeidere 3/4 av hele arbeidet med å reparere motorveien mellom de to kollektivbrukene. Den første dagen ble 2 2/5 km av denne motorveien reparert, den andre dagen 1 1/2 ganger mer enn den første, og den tredje dagen 5/8 av det som ble reparert de to første dagene til sammen. Finn lengden på motorveien mellom kollektivbruk.

564. Fyll ut de tomme plassene i tabellen, der S er arealet av rektangelet, EN- bunnen av rektangelet, a h-høyde (bredde) av rektangelet.

565. 1) Lengden på en rektangulær tomt er 120 m, og tomtens bredde er 2/5 av lengden. Finn omkretsen og området til nettstedet.

2) Bredden på den rektangulære seksjonen er 250 m, og lengden er 1 1/2 ganger bredden. Finn omkretsen og området til nettstedet.

566. 1) Omkretsen av rektangelet er 6 1/2 tomme, basen er 1/4 tomme større enn høyden. Finn arealet til dette rektangelet.

2) Omkretsen av rektangelet er 18 cm, høyden er 2 1/2 cm mindre enn basen. Finn arealet av rektangelet.

567. Regn ut arealene til figurene vist i figur 30 ved å dele dem inn i rektangler og finne dimensjonene til rektangelet ved måling.

568. 1) Hvor mange ark tørr gips vil det kreves for å dekke taket i et rom med lengde 4 1/2 m og bredde 4 m, hvis dimensjonene til gipsplaten er 2 m x l 1/2 m?

2) Hvor mange plater 4 1/2 m lange og 1/4 m brede trengs for å legge et gulv som er 4 1/2 m langt og 3 1/2 m bredt?

569. 1) En rektangulær tomt 560 m lang og 3/4 av lengden bred ble sådd med bønner. Hvor mange frø var nødvendig for å så tomten hvis det ble sådd 1 centner per 1 hektar?

2) En hvetehøst på 25 kvint per hektar ble samlet inn fra en rektangulær åker. Hvor mye hvete ble høstet fra hele åkeren hvis lengden på åkeren er 800 m og bredden er 3/8 av lengden?

570 . 1) En rektangulær tomt, 78 3/4 m lang og 56 4/5 m bred, er bebygd slik at 4/5 av dens areal er belagt med bygninger. Bestem arealet av land under bygningene.

2) På et rektangulært jordstykke, hvor lengden er 9/20 km og bredden er 4/9 av lengden, planlegger kollektivbruket å anlegge hage. Hvor mange trær vil bli plantet i denne hagen hvis et gjennomsnittlig areal på 36 kvm kreves for hvert tre?

571. 1) For normal dagslysbelysning av rommet er det nødvendig at arealet av alle vinduer er minst 1/5 av gulvarealet. Finn ut om det er nok lys i et rom med lengde 5 1/2 m og bredde 4 m. Har rommet ett vindu som måler 1 1/2 m x 2 m?

2) Bruk tilstanden til forrige oppgave, finn ut om det er nok lys i klasserommet ditt.

572. 1) Fjøset har dimensjoner på 5 1/2 m x 4 1/2 m x 2 1/2 m. Hvor mye høy (i vekt) får plass i denne låven hvis den er fylt til 3/4 av høyden og hvis 1 cu . m høy veier 82 kg?

2) Vedhaugen har formen rektangulært parallellepipedum, hvis dimensjoner er 2 1/2 m x 3 1/2 m x 1 1/2 m. Hva er vekten av vedhaugen hvis 1 cu. m ved veier 600 kg?

573. 1) Et rektangulært akvarium er fylt med vann opp til 3/5 av høyden. Lengden på akvariet er 1 1/2 m, bredde 4/5 m, høyde 3/4 m. Hvor mange liter vann helles i akvariet?

2) Et basseng i form av et rektangulært parallellepiped er 6 1/2 m langt, 4 m bredt og 2 m høyt Bassenget er fylt med vann opp til 3/4 av høyden. Beregn mengden vann som helles i bassenget.

574. Et gjerde må bygges rundt et rektangulært stykke land, 75 m langt og 45 m bredt. Hvor mange kubikkmeter med plater bør gå inn i konstruksjonen hvis tykkelsen på platen er 2 1/2 cm og høyden på gjerdet skal være 2 1/4 m?

575. 1) Hvilken vinkel er minuttet og timeviser klokken 13? klokken 15? klokken 17? klokken 21? kl 23:30?

2) Hvor mange grader vil timeviseren rotere på 2 timer? klokka 5? klokka 8? 30 min.?

3) Hvor mange grader inneholder en bue lik en halv sirkel? 1/4 sirkel? 1/24 av en sirkel? 5/24 sirkler?

576. 1) Bruk en gradskive, tegn: a) en rett vinkel; b) en vinkel på 30°; c) en vinkel på 60°; d) vinkel på 150°; e) en vinkel på 55°.

2) Bruk en gradskive, mål vinklene til figuren og finn summen av alle vinklene til hver figur (fig. 31).

577. Følg disse instruksjonene:

578. 1) Halvsirkelen er delt inn i to buer, hvorav den ene er 100° større enn den andre. Finn størrelsen på hver bue.

2) Halvsirkelen er delt inn i to buer, hvorav den ene er 15° mindre enn den andre. Finn størrelsen på hver bue.

3) Halvsirkelen er delt i to buer, hvorav den ene er dobbelt så stor som den andre. Finn størrelsen på hver bue.

4) Halvsirkelen er delt inn i to buer, hvorav den ene er 5 ganger mindre enn den andre. Finn størrelsen på hver bue.

579. 1) Diagrammet «Population Literacy in the USSR» (Fig. 32) viser antall lesekyndige per hundre mennesker av befolkningen. Basert på dataene i diagrammet og dets skala, bestemme antall lesekyndige menn og kvinner for hvert av de angitte årene.

Skriv resultatene i tabellen:

2) Bruk dataene fra diagrammet "Sovjetiske utsendinger til verdensrommet" (fig. 33), lag oppgaver.

580. 1) I følge kakediagrammet «Daglig rutine for en elev i femte klasse» (Fig. 34), fyll ut tabellen og svar på spørsmålene: hvilken del av dagen er tildelt søvn? til lekser? til skolen?

2) Lag et kakediagram om din daglige rutine.

Nå som vi har lært å addere og multiplisere individuelle brøker, kan vi se på mer komplekse strukturer. For eksempel, hva om det samme problemet innebærer å legge til, subtrahere og multiplisere brøker?

Først av alt må du konvertere alle brøker til uekte. Deretter utfører vi de nødvendige handlingene sekvensielt - i samme rekkefølge som for vanlige tall. Nemlig:

Eksponentiering gjøres først - bli kvitt alle uttrykk som inneholder eksponenter;
Deretter - divisjon og multiplikasjon;
Det siste trinnet er addisjon og subtraksjon.

Selvfølgelig, hvis det er parenteser i uttrykket, endres rekkefølgen av operasjoner - alt som er innenfor parentesen må telles først. Og husk om upassende brøker: du må bare fremheve hele delen når alle andre handlinger allerede er fullført.

La oss konvertere alle brøkene fra det første uttrykket til upassende, og deretter utføre følgende trinn:

La oss nå finne verdien av det andre uttrykket. Det er ingen brøker med en heltallsdel, men det er parenteser, så først utfører vi addisjon, og først deretter divisjon. Merk at 14 = 7 · 2. Deretter:

Tenk til slutt på det tredje eksemplet. Det er parentes og en grad her - det er bedre å telle dem separat. Med tanke på at 9 = 3 3, har vi:

Vær oppmerksom på det siste eksemplet. For å heve en brøk til en potens, må du separat heve telleren til denne potensen, og separat, nevneren.

Du kan bestemme annerledes. Hvis vi husker definisjonen av en grad, vil problemet reduseres til den vanlige multiplikasjonen av brøker:

Fleretasjes brøker

Til nå har vi kun vurdert «rene» brøker, når telleren og nevneren er vanlige tall. Dette er ganske i samsvar med definisjonen av en tallbrøk gitt i den aller første leksjonen.

Men hva om du legger et mer komplekst objekt i telleren eller nevneren? For eksempel en annen numerisk brøk? Slike konstruksjoner oppstår ganske ofte, spesielt når man jobber med lange uttrykk. Her er et par eksempler:

Det er bare én regel for å jobbe med brøker med flere etasjer: du må kvitte deg med dem umiddelbart. Å fjerne "ekstra" gulv er ganske enkelt, hvis du husker at skråstreken betyr standard delingsoperasjon. Derfor kan enhver brøk skrives om som følger:

Ved å bruke dette faktum og følge prosedyren, kan vi enkelt redusere enhver brøk med flere etasjer til en vanlig. Ta en titt på eksemplene:

Oppgave. Konverter brøker med flere etasjer til vanlige:

I hvert tilfelle omskriver vi hovedbrøken, og erstatter delelinjen med et divisjonstegn. Husk også at et hvilket som helst heltall kan representeres som en brøk med nevneren 1. Det vil si 12 = 12/1; 3 = 3/1. Vi får:

I det siste eksemplet ble brøkene annullert før den endelige multiplikasjonen.

Spesifikasjoner for arbeid med brøker på flere nivåer

Det er én subtilitet i brøker på flere nivåer som alltid må huskes, ellers kan du få feil svar, selv om alle beregningene var riktige. Ta en titt:

Telleren inneholder enkelttallet 7, og nevneren inneholder brøken 12/5;
Telleren inneholder brøken 7/12, og nevneren inneholder det separate tallet 5.

Så for en innspilling fikk vi to helt forskjellige tolkninger. Hvis du teller, vil svarene også være forskjellige:

For å sikre at posten alltid leses entydig, bruk en enkel regel: delelinjen til hovedbrøken må være lengre enn linjen til den nestede brøken. Gjerne flere ganger.

Hvis du følger denne regelen, bør brøkene ovenfor skrives som følger:

Ja, det er nok skjemmende og tar for mye plass. Men du vil telle riktig. Til slutt, et par eksempler hvor brøker med flere etasjer faktisk oppstår:

Oppgave. Finn betydningen av uttrykkene:

Så la oss jobbe med det første eksemplet. La oss konvertere alle brøker til uekte, og deretter utføre addisjons- og divisjonsoperasjoner:

La oss gjøre det samme med det andre eksemplet. La oss konvertere alle brøker til upassende og utføre de nødvendige operasjonene. For ikke å kjede leseren vil jeg utelate noen åpenbare beregninger. Vi har:

På grunn av det faktum at telleren og nevneren til de grunnleggende brøkene inneholder summer, blir regelen for å skrive fleretasjes brøker observert automatisk. I det siste eksemplet la vi også med vilje 46/1 i brøkform for å utføre divisjon.

Jeg vil også legge merke til at i begge eksemplene erstatter brøklinjen faktisk parentesen: først og fremst fant vi summen, og først deretter kvotienten.

Noen vil si at overgangen til uekte brøker i det andre eksemplet var klart overflødig. Kanskje dette er sant. Men ved å gjøre dette sikrer vi oss mot feil, for neste gang kan eksemplet vise seg å være mye mer komplisert. Velg selv hva som er viktigere: hastighet eller pålitelighet.

Denne artikkelen undersøker operasjoner på brøker. Regler for addisjon, subtraksjon, multiplikasjon, divisjon eller eksponentiering av brøker av formen A B vil bli dannet og begrunnet, hvor A og B kan være tall, numeriske uttrykk eller uttrykk med variable. Avslutningsvis vil eksempler på løsninger med detaljerte beskrivelser bli vurdert.

Yandex.RTB R-A-339285-1

Regler for å utføre operasjoner med generelle numeriske brøker

Numeriske brøker generelt syn ha en teller og en nevner som inneholder naturlige tall eller numeriske uttrykk. Hvis vi tar for oss brøker som 3 5, 2, 8 4, 1 + 2 3 4 (5 - 2), 3 4 + 7 8 2, 3 - 0, 8, 1 2 2, π 1 - 2 3 + π, 2 0, 5 ln 3, så er det klart at teller og nevner ikke bare kan ha tall, men også uttrykk av ulike typer.

Definisjon 1

Det er regler for hvilke operasjoner med vanlige brøker utføres. Den er også egnet for generelle fraksjoner:

Når du trekker fra brøker fra samme nevnere bare tellerne legges til, og nevneren forblir den samme, nemlig: a d ± c d = a ± c d, verdiene a, c og d ≠ 0 er noen tall eller numeriske uttrykk.
Når du legger til eller subtraherer en brøk med forskjellige nevnere, er det nødvendig å redusere den til en fellesnevner, og deretter addere eller subtrahere de resulterende brøkene med de samme eksponentene. Bokstavelig talt ser det slik ut: a b ± c d = a · p ± c · r s, hvor verdiene a, b ≠ 0, c, d ≠ 0, p ≠ 0, r ≠ 0, s ≠ 0 er reelle tall og b · p = d · r = s . Når p = d og r = b, så er a b ± c d = a · d ± c · d b · d.
Ved multiplisering av brøker utføres handlingen med tellere, deretter med nevnere, da får vi a b · c d = a · c b · d, hvor a, b ≠ 0, c, d ≠ 0 fungerer som reelle tall.
Når vi deler en brøk med en brøk, multipliserer vi den første med den andre inversen, det vil si at vi bytter teller og nevner: a b: c d = a b · d c.

Begrunnelse for reglene

Definisjon 2

Det er følgende matematiske punkter du bør stole på når du regner:

skråstreken betyr divisjonstegnet;
divisjon med et tall behandles som multiplikasjon med dens gjensidige verdi;
anvendelse av egenskapen til operasjoner med reelle tall;
anvendelse av den grunnleggende egenskapen til brøker og numeriske ulikheter.

Med deres hjelp kan du utføre transformasjoner av skjemaet:

a d ± c d = a · d - 1 ± c · d - 1 = a ± c · d - 1 = a ± c d; a b ± c d = a · p b · p ± c · r d · r = a · p s ± c · e s = a · p ± c · r s; a b · c d = a · d b · d · b · c b · d = a · d · a · d - 1 · b · c · b · d - 1 = = a · d · b · c · b · d - 1 · b · d - 1 = a · d · b · c b · d · b · d - 1 = = (a · c) · (b · d) - 1 = a · c b · d

Eksempler

I forrige avsnitt ble det sagt om operasjoner med brøker. Det er etter dette at brøken må forenkles. Dette emnet ble diskutert i detalj i avsnittet om konvertering av brøker.

La oss først se på et eksempel på å legge til og trekke fra brøker med samme nevner.

Eksempel 1

Gitt brøkene 8 2, 7 og 1 2, 7, er det i henhold til regelen nødvendig å legge til telleren og omskrive nevneren.

Løsning

Da får vi en brøkdel av formen 8 + 1 2, 7. Etter å ha utført tillegget får vi en brøkdel av formen 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3. Så, 8 2, 7 + 1 2, 7 = 8 + 1 2, 7 = 9 2, 7 = 90 27 = 3 1 3.

Svar: 8 2 , 7 + 1 2 , 7 = 3 1 3

Det finnes en annen løsning. Til å begynne med bytter vi til formen av en vanlig brøk, hvoretter vi utfører en forenkling. Det ser slik ut:

8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3

Eksempel 2

La oss trekke fra 1 - 2 3 · log 2 3 · log 2 5 + 1 en brøkdel av formen 2 3 3 · log 2 3 · log 2 5 + 1 .

Siden like nevnere er gitt, betyr det at vi regner ut en brøk med samme nevner. Det skjønner vi

1 - 2 3 log 2 3 log 2 5 + 1 - 2 3 3 log 2 3 log 2 5 + 1 = 1 - 2 - 2 3 3 log 2 3 log 2 5 + 1

Det finnes eksempler på å regne ut brøker med ulike nevnere. Et viktig poeng er reduksjon til en fellesnevner. Uten dette vil vi ikke kunne utføre ytterligere operasjoner med brøker.

Prosessen minner vagt om reduksjon til en fellesnevner. Det vil si at den minste felles divisor i nevneren søkes etter, hvoretter de manglende faktorene legges til brøkene.

Hvis fraksjonene som tilsettes ikke har felles faktorer, kan produktet deres bli en.

Eksempel 3

La oss se på eksemplet med å legge til brøk 2 3 5 + 1 og 1 2.

Løsning

I dette tilfellet er fellesnevneren produktet av nevnerne. Da får vi 2 · 3 5 + 1. Så, når vi setter tilleggsfaktorer, har vi at for den første brøken er den lik 2, og for den andre er den 3 5 + 1. Etter multiplikasjon reduseres brøkene til formen 4 2 · 3 5 + 1. Den generelle reduksjonen på 1 2 vil være 3 5 + 1 2 · 3 5 + 1. Vi legger til de resulterende brøkuttrykkene og får det

2 3 5 + 1 + 1 2 = 2 2 2 3 5 + 1 + 1 3 5 + 1 2 3 5 + 1 = = 4 2 3 5 + 1 + 3 5 + 1 2 3 5 + 1 = 4 + 3 5 + 1 2 3 5 + 1 = 5 + 3 5 2 3 5 + 1

Svar: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 3 5 + 1

Når vi har å gjøre med generelle brøker, så snakker vi vanligvis ikke om den laveste fellesnevneren. Det er ulønnsomt å ta produktet av tellerne som nevner. Først må du sjekke om det er et tall som er mindre i verdi enn produktet deres.

Eksempel 4

La oss se på eksemplet med 1 6 · 2 1 5 og 1 4 · 2 3 5, når produktet deres er lik 6 · 2 1 5 · 4 · 2 3 5 = 24 · 2 4 5. Da tar vi 12 · 2 3 5 som fellesnevner.

La oss se på eksempler på å multiplisere generelle brøker.

Eksempel 5

For å gjøre dette må du multiplisere 2 + 1 6 og 2 · 5 3 · 2 + 1.

Løsning

Etter regelen er det nødvendig å omskrive og skrive produktet av tellerne som en nevner. Vi får at 2 + 1 6 2 5 3 2 + 1 2 + 1 2 5 6 3 2 + 1. Når en brøk er multiplisert, kan du gjøre reduksjoner for å forenkle den. Deretter 5 · 3 3 2 + 1: 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10.

Ved å bruke regelen for overgang fra divisjon til multiplikasjon med en resiprok brøk får vi en brøk som er den resiproke av den gitte. For å gjøre dette byttes teller og nevner. La oss se på et eksempel:

5 3 3 2 + 1: 10 9 3 = 5 3 3 2 + 1 9 3 10

Deretter må de multiplisere og forenkle den resulterende brøken. Bli eventuelt kvitt irrasjonalitet i nevneren. Det skjønner vi

5 3 3 2 + 1: 10 9 3 = 5 3 3 9 3 10 2 + 1 = 5 2 10 2 + 1 = 3 2 2 + 1 = 3 2 - 1 2 2 + 1 2 - 1 = 3 2 - 1 2 2 2 - 1 2 = 3 2 - 1 2

Svar: 5 3 3 2 + 1: 10 9 3 = 3 2 - 1 2

Dette avsnittet gjelder når et tall eller numerisk uttrykk kan representeres som en brøk med en nevner lik 1, da regnes operasjonen med en slik brøk som et eget avsnitt. For eksempel viser uttrykket 1 6 · 7 4 - 1 · 3 at roten av 3 kan erstattes med et annet 3 1-uttrykk. Da vil denne oppføringen se ut som å multiplisere to brøker av formen 1 6 · 7 4 - 1 · 3 = 1 6 · 7 4 - 1 · 3 1.

Utføre operasjoner på brøker som inneholder variabler

Reglene omtalt i den første artikkelen gjelder for operasjoner med brøker som inneholder variabler. Tenk på subtraksjonsregelen når nevnerne er like.

Det er nødvendig å bevise at A, C og D (D ikke lik null) kan være et hvilket som helst uttrykk, og likheten A D ± C D = A ± C D er ekvivalent med rekkevidden av tillatte verdier.

Det er nødvendig å ta et sett med ODZ-variabler. Da må A, C, D ta de tilsvarende verdiene a 0 , c 0 og d 0. Substitusjon av formen A D ± C D resulterer i en forskjell på formen a 0 d 0 ± c 0 d 0, hvor vi ved å bruke addisjonsregelen får en formel av formen a 0 ± c 0 d 0. Hvis vi erstatter uttrykket A ± C D, får vi samme brøkdel av formen a 0 ± c 0 d 0. Herfra konkluderer vi med at den valgte verdien som tilfredsstiller ODZ, A ± C D og A D ± C D anses like.

For enhver verdi av variablene vil disse uttrykkene være like, det vil si at de kalles identisk like. Dette betyr at dette uttrykket anses som en bevisbar likhet av formen A D ± C D = A ± C D .

Eksempler på å legge til og trekke fra brøker med variabler

Når du har de samme nevnerne, trenger du bare å legge til eller trekke fra tellerne. Denne brøkdelen kan forenkles. Noen ganger må du jobbe med brøker som er identisk like, men ved første øyekast er dette ikke merkbart, siden noen transformasjoner må utføres. For eksempel, x 2 3 x 1 3 + 1 og x 1 3 + 1 2 eller 1 2 sin 2 α og sin a cos a. Oftest kreves det en forenkling av det opprinnelige uttrykket for å se de samme nevnerne.

Eksempel 6

Regn ut: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) , x - 1 x - 1 + x x + 1 .

Løsning

For å gjøre utregningen må du trekke fra brøker som har samme nevner. Da får vi at x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + 1 - 5 - x x + x - 2 . Deretter kan du utvide parentesene og legge til lignende termer. Vi får at x 2 + 1 - 5 - x x + x - 2 = x 2 + 1 - 5 + x x + x - 2 = x 2 + x - 4 x + x - 2
Siden nevnerne er de samme, gjenstår det bare å legge sammen tellerne, slik at nevneren blir igjen: l g 2 x + 4 x (l g x + 2) + 4 l g x x (l g x + 2) = l g 2 x + 4 + 4 x (l g x + 2)
Tillegget er fullført. Man kan se at det er mulig å redusere brøken. Telleren kan brettes ved å bruke formelen for kvadratet av summen, så får vi (l g x + 2) 2 fra forkortede multiplikasjonsformler. Da får vi det
l g 2 x + 4 + 2 l g x x (l g x + 2) = (l g x + 2) 2 x (l g x + 2) = l g x + 2 x
Gitt brøker av formen x - 1 x - 1 + x x + 1 med forskjellige nevnere. Etter transformasjonen kan du gå videre til tillegg.

La oss vurdere en todelt løsning.

Den første metoden er at nevneren til den første brøken faktoriseres ved hjelp av kvadrater, med påfølgende reduksjon. Vi får en brøkdel av formen

x - 1 x - 1 = x - 1 (x - 1) x + 1 = 1 x + 1

Så x - 1 x - 1 + x x + 1 = 1 x + 1 + x x + 1 = 1 + x x + 1 .

I dette tilfellet er det nødvendig å kvitte seg med irrasjonalitet i nevneren.

1 + x x + 1 = 1 + x x - 1 x + 1 x - 1 = x - 1 + x x - x x - 1

Den andre metoden er å multiplisere telleren og nevneren til den andre brøken med uttrykket x - 1. Dermed blir vi kvitt irrasjonalitet og går videre til å legge til brøker med samme nevner. Deretter

x - 1 x - 1 + x x + 1 = x - 1 x - 1 + x x - 1 x + 1 x - 1 = = x - 1 x - 1 + x x - x x - 1 = x - 1 + x · x - x x - 1

Svar: 1) x 2 + 1 x + x - 2 - 5 - x x + x - 2 = x 2 + x - 4 x + x - 2, 2) l g 2 x + 4 x · (l g x + 2) + 4 · l g x x · (l g x + 2) = l g x + 2 x, 3) x - 1 x - 1 + x x + 1 = x - 1 + x · x - x x - 1 .

I det siste eksemplet fant vi at reduksjon til en fellesnevner er uunngåelig. For å gjøre dette må du forenkle brøkene. Når du legger til eller trekker fra, må du alltid se etter en fellesnevner, som ser ut som produktet av nevnerne med tilleggsfaktorer lagt til tellerne.

Eksempel 7

Regn ut verdiene til brøkene: 1) x 3 + 1 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) (2 x - 4) - sin x x 5 ln (x + 1) (2 x - 4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x

Løsning

Ingen komplekse beregninger nevneren er ikke nødvendig, så du må velge produktet deres på formen 3 x 7 + 2 · 2, og deretter velge x 7 + 2 · 2 for den første brøken som en tilleggsfaktor, og 3 for den andre. Når vi multipliserer, får vi en brøkdel av formen x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 3 x 7 + 2 2 + 3 1 3 x 7 + 2 2 = = x x 7 + 2 2 + 3 3 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2
Man kan se at nevnerne presenteres i form av et produkt, noe som betyr at ytterligere transformasjoner er unødvendige. Fellesnevneren vil anses å være et produkt av formen x 5 · ln 2 x + 1 · 2 x - 4 . Derfor x 4 er en tilleggsfaktor til den første brøken, og ln(x + 1) til den andre. Så trekker vi fra og får:
x + 1 x · ln 2 (x + 1) · 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x + 1 · x 4 x 5 · ln 2 (x + 1) ) · 2 x - 4 - sin x · ln x + 1 x 5 · ln 2 (x + 1) · (2 x - 4) = = x + 1 · x 4 - sin x · ln (x + 1) ) x 5 · ln 2 (x + 1) · (2 x - 4) = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4)
Dette eksemplet gir mening når du arbeider med brøknevnere. Det er nødvendig å bruke formlene for forskjellen av kvadrater og kvadratet av summen, siden de vil gjøre det mulig å gå videre til et uttrykk på formen 1 cos x - x · cos x + x + 1 (cos x + x) 2. Man kan se at brøkene er redusert til en fellesnevner. Vi får at cos x - x · cos x + x 2 .

Da får vi det

1 cos 2 x - x + 1 cos 2 x + 2 cos x x + x = = 1 cos x - x cos x + x + 1 cos x + x 2 = = cos x + x cos x - x cos x + x 2 + cos x - x cos x - x cos x + x 2 = = cos x + x + cos x - x cos x - x cos x + x 2 = 2 cos x cos x - x cos x + x 2

Svar:

1) x 3 + 1 x 7 + 2 2 = x x 7 + 2 2 x + 3 3 x 7 + 2 2, 2) x + 1 x ln 2 (x + 1) 2 x - 4 - sin x x 5 · ln (x + 1) · 2 x - 4 = = x · x 4 + x 4 - sin x · ln (x + 1) x 5 · ln 2 (x + 1) · ( 2 x - 4) , 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x = 2 · cos x cos x - x · cos x + x 2 .

Eksempler på å multiplisere brøker med variabler

Når du multipliserer brøker, multipliseres telleren med telleren og nevneren med nevneren. Da kan du bruke reduksjonsegenskapen.

Eksempel 8

Multipliser brøkene x + 2 · x x 2 · ln x 2 · ln x + 1 og 3 · x 2 1 3 · x + 1 - 2 sin 2 · x - x.

Løsning

Multiplikasjon må gjøres. Det skjønner vi

x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = = x - 2 x 3 x 2 1 3 x + 1 - 2 x 2 ln x 2 ln x + 1 sin (2 x - x)

Tallet 3 flyttes til første plass for å gjøre det lettere å regne ut, og du kan redusere brøken med x 2, så får vi et uttrykk for formen

3 x - 2 x x 1 3 x + 1 - 2 ln x 2 ln x + 1 sin (2 x - x)

Svar: x + 2 x x 2 ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x) = 3 x - 2 x x 1 3 x + 1 - 2 ln x 2 · ln x + 1 · sin (2 · x - x) .

Inndeling

Deling av brøker ligner på multiplikasjon, siden den første brøken multipliseres med den andre resiproke. Hvis vi for eksempel tar brøken x + 2 x x 2 ln x 2 ln x + 1 og deler på 3 x 2 1 3 x + 1 - 2 sin 2 x - x, så kan det skrives som

x + 2 · x x 2 · ln x 2 · ln x + 1: 3 · x 2 1 3 · x + 1 - 2 sin (2 · x - x) , erstatt deretter med et produkt av formen x + 2 · x x 2 · ln x 2 ln x + 1 3 x 2 1 3 x + 1 - 2 sin (2 x - x)

Eksponentiering

La oss gå videre til å vurdere operasjoner med generelle brøker med eksponentiering. Hvis du har en grad med naturlig indikator, da anses handlingen som multiplikasjon av like brøker. Men det anbefales å bruke en generell tilnærming basert på egenskapene til grader. Alle uttrykk A og C, hvor C ikke er identisk lik null, og enhver reell r på ODZ for et uttrykk på formen A C r er likheten A C r = A r C r gyldig. Resultatet er en brøkdel hevet til en potens. Vurder for eksempel:

x 0, 7 - π · ln 3 x - 2 - 5 x + 1 2, 5 = = x 0, 7 - π · ln 3 x - 2 - 5 2, 5 x + 1 2, 5

Prosedyre for å utføre operasjoner med brøker

Operasjoner på brøker utføres etter visse regler. I praksis legger vi merke til at et uttrykk kan inneholde flere brøker eller brøkuttrykk. Deretter er det nødvendig å utføre alle handlinger i streng rekkefølge: heve til en potens, multiplisere, dele, deretter legge til og subtrahere. Hvis det er parenteser, utføres den første handlingen i dem.

Eksempel 9

Regn ut 1 - x cos x - 1 c o s x · 1 + 1 x .

Løsning

Siden vi har samme nevner, så 1 - x cos x og 1 c o s x, men subtraksjoner kan ikke utføres i henhold til regelen; først utføres handlingene i parentes, deretter multiplikasjon og deretter addisjon. Så når vi regner ut, får vi det

1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x

Når du erstatter uttrykket med det opprinnelige, får vi at 1 - x cos x - 1 cos x · x + 1 x. Når vi multipliserer brøker har vi: 1 cos x · x + 1 x = x + 1 cos x · x. Etter å ha gjort alle erstatningene får vi 1 - x cos x - x + 1 cos x · x. Nå må du jobbe med brøker som har forskjellige nevnere. Vi får:

x · 1 - x cos x · x - x + 1 cos x · x = x · 1 - x - 1 + x cos x · x = = x - x - x - 1 cos x · x = - x + 1 cos x x

Svar: 1 - x cos x - 1 cos x · 1 + 1 x = - x + 1 cos x · x .

Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter

Denne delen dekker operasjoner med vanlige brøker. Hvis det er nødvendig å utføre en matematisk operasjon med blandede tall, er det nok å konvertere den blandede brøken til en ekstraordinær brøk, utføre de nødvendige operasjonene og om nødvendig presentere det endelige resultatet igjen i form av et blandet tall . Denne operasjonen vil bli beskrevet nedenfor.

Reduserer en brøkdel

Matematisk operasjon. Reduserer en brøkdel

For å redusere brøken \frac(m)(n) må du finne den største felles divisor for telleren og nevneren: gcd(m,n), og deretter dele telleren og nevneren til brøken med dette tallet. Hvis GCD(m,n)=1, kan ikke brøken reduseres. Eksempel: \frac(20)(80)=\frac(20:20)(80:20)=\frac(1)(4)

Vanligvis ser det ut til å umiddelbart finne den største felles divisoren å være en vanskelig oppgave, og i praksis reduseres en brøk i flere trinn, trinn for trinn isolere åpenbare felles faktorer fra telleren og nevneren. \frac(140)(315)=\frac(28\cdot5)(63\cdot5)=\frac(4\cdot7\cdot5)(9\cdot7\cdot5)=\frac(4)(9)

Redusere brøker til en fellesnevner

Matematisk operasjon. Redusere brøker til en fellesnevner

For å bringe to brøker \frac(a)(b) og \frac(c)(d) til en fellesnevner trenger du:

finn det minste felles multiplum av nevnerne: M=LMK(b,d);
multipliser telleren og nevneren til den første brøken med M/b (hvoretter nevneren til brøken blir lik tallet M);
multipliser telleren og nevneren til den andre brøken med M/d (hvoretter nevneren til brøken blir lik tallet M).

Dermed transformerer vi de opprinnelige brøkene til brøker med de samme nevnerne (som vil være lik tallet M).

For eksempel har brøkene \frac(5)(6) og \frac(4)(9) LCM(6,9) = 18. Da: \frac(5)(6)=\frac(5\cdot3) (6 \cdot3)=\frac(15)(18);\quad\frac(4)(9)=\frac(4\cdot2)(9\cdot2)=\frac(8)(18) . Dermed har de resulterende brøkene en fellesnevner.

I praksis er det ikke alltid en enkel oppgave å finne det minste felles multiplum (LCM) av nevnere. Derfor velges et tall som er lik produktet av nevnerne til de opprinnelige brøkene som fellesnevner. For eksempel reduseres brøkene \frac(5)(6) og \frac(4)(9) til en fellesnevner N=6\cdot9:

\frac(5)(6)=\frac(5\cdot9)(6\cdot9)=\frac(45)(54);\quad\frac(4)(9)=\frac(4\cdot6)( 9\cdot6)=\frac(24)(54)

Sammenligning av brøker

Matematisk operasjon. Sammenligning av brøker

For å sammenligne to vanlige brøker trenger du:

sammenligne tellerne til de resulterende brøkene; en brøkdel med en større teller vil være større.

For eksempel, \frac(9)(14)

Når du sammenligner brøker, er det flere spesielle tilfeller:

Fra to brøker med de samme nevnerne Brøken hvis teller er større, er større. For eksempel, \frac(3)(15)
Fra to brøker med de samme tellerne Jo større er brøken hvis nevner er mindre. For eksempel, \frac(4)(11)>\frac(4)(13)
Den brøken som samtidig større teller og mindre nevner, mer. For eksempel, \frac(11)(3)>\frac(10)(8)

Merk følgende! Regel 1 gjelder for alle brøker hvis fellesnevneren er et positivt tall. Regel 2 og 3 gjelder for positive brøker (de med både teller og nevner større enn null).

Legge til og trekke fra brøker

Matematisk operasjon. Legge til og trekke fra brøker

For å legge til to brøker trenger du:

bringe dem til en fellesnevner;
legg til tellerne og la nevneren være uendret.

Eksempel: \frac(7)(9)+\frac(4)(7)=\frac(7\cdot7)(9\cdot7)+\frac(4\cdot9)(7\cdot9)=\frac(49) )(63)+\frac(36)(63)=\frac(49+36)(63)=\frac(85)(63)

For å trekke en annen fra en brøk, trenger du:

redusere brøker til en fellesnevner;
Trekk telleren til den andre brøken fra telleren til den første brøken og la nevneren stå uendret.

Eksempel: \frac(4)(15)-\frac(3)(5)=\frac(4)(15)-\frac(3\cdot3)(5\cdot3)=\frac(4)(15) -\frac(9)(15)=\frac(4-9)(15)=\frac(-5)(15)=-\frac(5)(3\cdot5)=-\frac(1)( 3)

Hvis de opprinnelige brøkene i utgangspunktet har en fellesnevner, hoppes trinn 1 (reduksjon til en fellesnevner) over.

Konvertering av et blandet tall til en uekte brøk og omvendt

Matematisk operasjon. Konvertering av et blandet tall til en uekte brøk og omvendt

For å konvertere en blandet brøk til en uekte brøk, summerer du ganske enkelt hele delen av den blandede brøken med brøkdelen. Resultatet av en slik sum vil være en uekte brøk, hvis teller er lik summen av produktet av hele delen med nevneren til brøken med telleren til den blandede brøken, og nevneren vil forbli den samme. For eksempel, 2\frac(6)(11)=2+\frac(6)(11)=\frac(2\cdot11)(11)+\frac(6)(11)=\frac(2\cdot11+ 6)(11)=\frac(28)(11)

Slik konverterer du en uekte brøk til et blandet tall:

del telleren til en brøk med nevneren;
skriv resten av inndelingen i telleren og la nevneren være den samme;
skriv resultatet av divisjonen som en heltallsdel.

For eksempel, brøken \frac(23)(4) . Når du deler 23:4=5,75, det vil si at hele delen er 5, er resten av divisjonen 23-5*4=3. Deretter vil det blandede tallet skrives: 5\frac(3)(4) . \frac(23)(4)=\frac(5\cdot4+3)(4)=5\frac(3)(4)

Konvertering av en desimal til en brøk

Matematisk operasjon. Konvertering av en desimal til en brøk

For å konvertere en desimalbrøk til en vanlig brøk, må du:

ta n-te potens av ti som nevner (her er n antall desimaler);
som teller, ta tallet etter desimaltegnet (hvis heltallsdelen av det opprinnelige tallet ikke er lik null, ta alle de innledende nullene også);
Heltallsdelen som ikke er null er skrevet i telleren helt i begynnelsen; null heltallsdelen er utelatt.

Eksempel 1: 0.0089=\frac(89)(10000) (det er 4 desimaler, så nevneren har 10 4 =10000, siden heltallsdelen er 0, inneholder telleren tallet etter desimaltegnet uten innledende nuller)

Eksempel 2: 31.0109=\frac(310109)(10000) (i telleren skriver vi tallet etter desimaltegnet med alle nuller: "0109", og før det legger vi til hele delen av det opprinnelige tallet "31")

Hvis hele delen av en desimalbrøk ikke er null, kan den konverteres til en blandet brøk. For å gjøre dette konverterer vi tallet til vanlig brøk som om hele delen var lik null (punkt 1 og 2), og vi skriver ganske enkelt hele delen om før brøken - dette vil være hele delen av et blandet tall. Eksempel:

3.014=3\frac(14)(100)

For å konvertere en brøk til en desimal deler du bare telleren på nevneren. Noen ganger ender du opp med en uendelig desimal. I dette tilfellet er det nødvendig å avrunde til ønsket desimal. Eksempler:

\frac(401)(5)=80.2;\quad \frac(2)(3)\approx0.6667

Multiplisere og dele brøker

Matematisk operasjon. Multiplisere og dele brøker

For å multiplisere to vanlige brøker, må du multiplisere tellerne og nevnerne til brøkene.

\frac(5)(9)\cdot\frac(7)(2)=\frac(5\cdot7)(9\cdot2)=\frac(35)(18)

For å dele en vanlig brøk med en annen, må du multiplisere den første brøken med den gjensidige av den andre ( gjensidig brøk- en brøk der teller og nevner er byttet om.

\frac(5)(9):\frac(7)(2)=\frac(5)(9)\cdot\frac(2)(7)=\frac(5\cdot2)(9\cdot7)= \frac(10)(63)

Hvis en av brøkene er naturlig tall, så forblir reglene ovenfor for multiplikasjon og divisjon gjeldende. Du trenger bare å ta hensyn til at et heltall er den samme brøken, hvis nevner er lik en. For eksempel: 3:\frac(3)(7)=\frac(3)(1):\frac(3)(7)=\frac(3)(1)\cdot\frac(7)(3) = \frac(3\cdot7)(1\cdot3)=\frac(7)(1)=7

1. Regelen for å legge til brøker med de samme nevnerne:

Eksempel 1:

Eksempel 2:

Regel for å legge til brøker med forskjellige nevnere:

Eksempel 1:

Eksempel 2:

Her ble ikke nevnerne multiplisert, men den minste felles faktoren a2 ble tatt.
(Nevneren har den høyeste potensen 2.)
En tilleggsfaktor for den første brøken er 1, for den andre er det a.

2. Regel for å trekke fra brøker med like nevnere:

Regel for å trekke fra brøker med forskjellige nevnere:

3. Regel for å multiplisere vanlige brøker:

4. Regel for å dele brøker:

Eksempel:

Vanlig (enkel) brøk. Teller og nevner av en brøk.
Riktige og uekte brøker. Blandet tall.
Ufullstendig kvotient. Heltalls- og brøkdeler. Omvendte brøker. En del av en enhet eller flere deler av den kalles vanlig eller enkel brøk. Antallet like deler som enheten er delt inn i kalles nevneren, og antall deler som tas kalles telleren. Brøken skrives som:

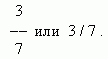
Her er 3 telleren, 7 er nevneren.

Hvis telleren er mindre enn nevneren, er brøken mindre enn 1 og kalles riktig brøk. Hvis telleren er lik nevneren, er brøken lik 1. Hvis telleren er større enn nevneren, er brøken større enn 1. I begge de sistnevnte tilfellene kalles brøken uegentlig. Hvis telleren er delt med nevneren, er denne brøken lik kvotienten til divisjonen: 63 / 7 = 9. Hvis divisjonen utføres med en rest, kan denne uekte brøken representeres blandet tall:

Her 9 – ufullstendig kvotient(heltallsdel av et blandet tall), 2 – resten (teller av brøkdelen), 7 – nevner.
Det er ofte nødvendig å løse det omvendte problemet - reversere et blandet tall til en brøkdel. For å gjøre dette, multipliser heltallsdelen av det blandede tallet med nevneren og legg til telleren til brøkdelen. Dette vil være telleren til fellesbrøken, men nevneren forblir den samme.

Resiproke fraksjoner er to fraksjoner hvis produkt er lik 1. For eksempel 3/7 og 7/3; 15/1 og 1/15 osv.

Brøkekspansjon. Reduserer en brøkdel. Sammenligning av brøker.
Reduksjon til en fellesnevner. Addisjon og subtraksjon brøker.
Multiplisere brøker. Inndeling av brøker
Brøkekspansjon.Verdien av en brøk endres ikke hvis dens teller og nevner multipliseres med det samme tallet annet enn null ved å utvide brøken. For eksempel

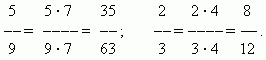
Reduserer en brøkdel. Verdien av en brøk endres ikke hvis du deler telleren og nevneren med samme tall bortsett fra null.. Denne transformasjonen kallesredusere en brøkdel. For eksempel,

Sammenligning av brøker.Av to brøker med samme tellere, er den som har mindre nevner større:

Av to brøker med samme nevner, er den hvis teller er større større:

For å sammenligne brøker som har forskjellige tellere og nevnere, må du utvide dem for å bringe dem til en fellesnevner.
EKSEMPEL Sammenlign to brøker:

Transformasjonen som brukes her kalles bringe brøker til en fellesnevner.
Legge til og trekke fra brøker.Hvis nevnerne til brøkene er de samme, må du legge til tellerne for å legge til brøkene, og for å trekke fra brøkene må du trekke fra tellerne deres (i samme rekkefølge). Den resulterende summen eller differansen vil være telleren for resultatet; nevneren vil forbli den samme. Hvis nevnerne til brøkene er forskjellige, må du først redusere brøkene til en fellesnevner. Når du legger til blandede tall, legges hele og brøkdeler til hver for seg. Når du trekker fra blandede tall, anbefaler vi først å konvertere dem til uekte brøker, deretter trekke det ene fra det andre, og deretter konvertere resultatet igjen, om nødvendig, til blandet tallform.
EKSEMPEL

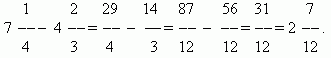
Multiplisere brøker.Å multiplisere et tall med en brøk betyr å multiplisere det med telleren og dele produktet på nevneren. Derfor har vi en generell regel for å multiplisere brøker:for å multiplisere brøker, må du multiplisere deres tellere og nevnere hver for seg og dele det første produktet på det andre.
EKSEMPEL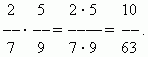
Å dele brøker. For å dele et visst tall med en brøk, er det nødvendig å multiplisere dette tallet med den gjensidige brøken Denne regelen følger av definisjonen av divisjon (se avsnittet "Aritmetiske operasjoner").
EKSEMPEL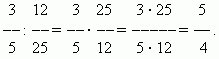

Desimal. Hele delen. Desimal tegn.
Desimaler. Egenskaper til desimalbrøker.
Periodisk desimalbrøk. Periode
Desimaler resultatet av å dele en med ti, hundre, tusen osv. deler. Disse brøkene er veldig praktiske for beregninger, siden de er basert på det samme posisjonssystemet som telling og skriving av heltall er basert på. Takket være dette er notasjonen og reglene for arbeid med desimalbrøker i hovedsak de samme som for hele tall. Når du skriver desimalbrøker, er det ikke nødvendig å markere nevneren; dette bestemmes av plassen som opptas av det tilsvarende sifferet. Først er det skrevet hele delen tall, og legg deretter til høyredesimal tegn. Det første sifferet etter desimaltegnet betyr antall tideler, det andre - antall hundredeler, det tredje - antall tusendeler osv. Tallene etter desimaltegn kallesdesimaler.
EKSEMPEL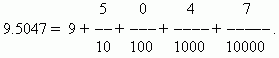
En av fordelene med desimalbrøker er at de lett reduseres til vanlige brøker: tallet etter desimaltegnet (i vårt tilfelle 5047) er telleren; nevneren er lik n -te potens av 10, hvor n - antall desimaler (i vårt tilfelle n = 4):
Hvis desimalbrøken ikke inneholder en heltallsdel, plasseres en null foran desimaltegnet:

Egenskaper til desimalbrøker.

1. Desimalen endres ikke hvis du legger til nuller til høyre:

2. Desimalbrøken endres ikke hvis du fjerner nullene som er plassert
på slutten av desimalen:

0.00123000 = 0.00123 .

OBS! Du kan ikke fjerne nuller som ikke er plassert på slutten desimal!br />

Disse egenskapene lar deg raskt multiplisere og dele desimaler med 10, 100, 1000 osv.

Periodisk desimal inneholder en uendelig repeterende gruppe tall kalt en periode. Perioden er skrevet i parentes. For eksempel, 0,12345123451234512345… = 0.(12345).

EKSEMPEL Hvis vi deler 47 på 11, får vi 4,27272727... = 4.(27).

Multiplisere desimaler.
Dele desimaler.

Legge til og trekke fra desimaler. Disse operasjonene utføres på samme måte som å legge til og trekke fra heltall. Du trenger bare å skrive ned de tilsvarende desimalene under hverandre.
EKSEMPEL

Multiplisere desimaler. På det første trinnet multipliserer vi desimalbrøker som hele tall, uten å ta hensyn til desimaltegnet. Da gjelder følgende regel: antall desimaler i produktet er lik summen av desimalene i alle faktorer.
Merk: før du setter desimaltegnet innproduktet kan ikke kasseres med etterfølgende nuller!
EKSEMPEL

Summen av tallene desimaler i faktorene er lik: 3 + 4 = 7. Summen av tallene i produktet er 6. Derfor må du legge til en null til venstre: 0197056 og sette et desimaltegn foran: 0,0197056.
Desimaldeling
Å dele en desimal på et helt tall
Hvis utbytte er mindre enn divisor, skriv en null i heltallsdelen av kvotienten og sett et desimaltegn etter den. Deretter, uten å ta hensyn til desimalpunktet til utbyttet, legger vi det neste sifferet i brøkdelen til dens heltallsdel og sammenligner igjen den resulterende heltallsdelen av utbyttet med divisoren. Hvis det nye tallet igjen er mindre enn divisoren, setter vi en ny null etter desimaltegnet i kvotienten og legger til neste siffer i brøkdelen til hele delen av utbyttet. Vi gjentar denne prosessen til det resulterende utbyttet blir større enn divisoren. Etter dette utføres divisjon som for heltall. Hvis utbyttet er større enn eller lik deleren, først deler vi hele delen, skriver resultatet av divisjonen i kvotienten og setter et desimaltegn. Etter dette fortsetter divisjonen som for heltall.
EKSEMPEL Del 1,328 med 64.
Løsning: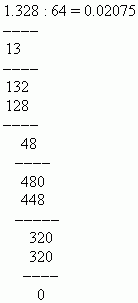
Å dele en desimalbrøk med en annen.
Først overfører vi desimalpunktene i utbyttet og divisoren til antall desimalplasser i divisoren, det vil si at vi gjør divisoren til et heltall. Nå utfører vi deling som i forrige tilfelle.
EKSEMPEL Del 0,04569 med 0,0006.
Løsning: Flytt desimaltegn 4 posisjoner til høyre og del 456,9 på 6:

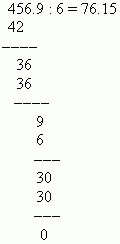
For å konvertere en desimalbrøk til en vanlig brøk, må du ta tallet etter desimaltegnet som teller, og ta n-te potens av ti som nevner (her er n antall desimaler). Heltallsdelen som ikke er null er lagret i en vanlig brøk; null heltallsdelen er utelatt. For eksempel:
For å konvertere en brøk til en desimal, må du dele telleren på nevneren i henhold til delingsreglene.
EKSEMPEL Konverter 5/8 til en desimal.
Løsning: Å dele 5 med 8 gir 0,625. (Regningen vær så snill!).
I de fleste tilfeller kan denne prosessen fortsette på ubestemt tid. Da er det umulig å nøyaktig konvertere en brøk til en desimal. Men i praksis er dette aldri nødvendig. Delingen avbrytes dersom desimalene av interesse allerede er oppnådd.
EKSEMPEL Konverter 1/3 til en desimal.
Løsning: Å dele 1 med 3 vil være uendelig: 1:3 = 0,3333... .
Sjekk det ut!