Даммигийн деривативыг шийдвэрлэх: тодорхойлолт, хэрхэн олох, шийдлийн жишээ. Деривативыг тооцох дүрэм Нарийн төвөгтэй функцийн дериватив u v
Мөн нийлмэл функцийн деривативын тухай теорем, томъёолол нь дараах байдалтай байна.
1) $u=\varphi (x)$ функц нь хэзээ нэгэн цагт $x_0$ дериватив $u_(x)"=\varphi"(x_0)$, 2) $y=f(u)$ функцтэй байг. харгалзах цэг дээр $u_0=\varphi (x_0)$ дериватив $y_(u)"=f"(u)$ байна. Дараа нь дурдсан цэг дэх $y=f\left(\varphi (x) \right)$ нийлмэл функц нь мөн $f(u)$ ба $\varphi ( функцуудын деривативын үржвэртэй тэнцүү деривативтай болно. x)$:
$$ \left(f(\varphi (x))\right)"=f_(u)"\left(\varphi (x_0) \баруун)\cdot \varphi"(x_0) $$
эсвэл богино тэмдэглэгээгээр: $y_(x)"=y_(u)"\cdot u_(x)"$.
Энэ хэсгийн жишээнүүдэд бүх функцууд нь $y=f(x)$ хэлбэртэй байна (өөрөөр хэлбэл, бид зөвхөн нэг хувьсагчийн $x$ функцийг авч үздэг). Үүний дагуу бүх жишээн дээр $y"$ деривативыг $x$ хувьсагчтай холбоотойгоор авдаг. Дериватив нь $x$ хувьсагчтай холбоотой гэдгийг онцлон тэмдэглэхийн тулд $y"_x$ гэж ихэвчлэн $y-ийн оронд бичдэг. "$.
1, 2, 3 дугаар жишээнүүд нь деривативыг олох нарийвчилсан үйл явцыг тоймлон харуулав. нарийн төвөгтэй функцууд. Жишээ №4 нь дериватив хүснэгтийг илүү бүрэн дүүрэн ойлгоход зориулагдсан бөгөөд үүнтэй танилцах нь зүйтэй юм.
1-3-р жишээн дэх материалыг судалсны дараа 5, 6, 7-р жишээнүүдийг бие даан шийдвэрлэхийг зөвлөж байна. №5, №6, 7-р жишээнүүд нь богино хэмжээний шийдлийг агуулдаг бөгөөд ингэснээр уншигч өөрийн үр дүнгийн зөв эсэхийг шалгах боломжтой болно.
Жишээ №1
$y=e^(\cos x)$ функцийн уламжлалыг ол.
Бид $y"$ нийлмэл функцийн деривативыг олох хэрэгтэй. $y=e^(\cos x)$ тул $y"=\left(e^(\cos x)\right)"$. $ \left(e^(\cos x)\right)"$ деривативыг ол. Бид деривативын хүснэгтээс 6-р томьёог ашиглана. 6-р томьёог ашиглахын тулд бидний тохиолдолд $u=\cos x$ гэдгийг анхаарч үзэх хэрэгтэй. Цаашдын шийдэл нь 6-р томьёонд $u$-ийн оронд $\cos x$ илэрхийллийг орлуулахад л оршино.
$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)" \tag (1.1)$$
Одоо бид $(\cos x)"$ илэрхийллийн утгыг олох хэрэгтэй. Бид үүнээс 10-р томьёог сонгон деривативын хүснэгт рүү дахин шилжинэ. $u=x$-г 10-р томьёонд орлуулбал бид дараах байдалтай байна. : $(\cos x)"=-\ sin x\cdot x"$. Одоо (1.1) тэгш байдлыг үргэлжлүүлж, олсон үр дүнгээр нэмэгдүүлье:
$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x") \tag (1.2) $$
$x"=1$ тул бид тэгш байдлыг үргэлжлүүлнэ (1.2):
$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x")=e^(\cos x)\cdot (-\sin x\cdot 1)=-\sin x\cdot e^(\cos x) \tag (1.3) $$
Тэгэхлээр (1.3) тэгшитгэлээс бидэнд: $y"=-\sin x\cdot e^(\cos x)$ байна. Мэдээжийн хэрэг, тайлбар болон завсрын тэгшитгэлийг ихэвчлэн алгасаж, деривативын олдворыг нэг мөрөнд бичнэ. тэгш байдлын хувьд ( 1.3) Тэгэхээр нийлмэл функцийн дериватив олдсон тул хариултыг бичих л үлдлээ.
Хариулт: $y"=-\sin x\cdot e^(\cos x)$.
Жишээ №2
$y=9\cdot \arctg^(12)(4\cdot \ln x)$ функцийн уламжлалыг ол.
Бид $y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"$ деривативыг тооцоолох хэрэгтэй. Эхлэхийн тулд тогтмолыг (жишээ нь 9-ийн тоог) дериватив тэмдгээс хасаж болно гэдгийг анхаарна уу.
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \баруун)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)" \tag (2.1) $$
Одоо $\left(\arctg^(12)(4\cdot \ln x) \right)"$ илэрхийлэл рүү шилжье. Деривативын хүснэгтээс хүссэн томьёо сонгоход хялбар болгохын тулд би илэрхийллийг танилцуулъя. Энэ хэлбэрээр асуултанд: $\left( \left(\arctg(4\cdot \ln x) \right)^(12)\right)"$. Одоо 2-р томъёог ашиглах шаардлагатай байгаа нь тодорхой байна, i.e. $\left(u^\alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Энэ томьёонд $u=\arctg(4\cdot \ln x)$ болон $\alpha=12$-г орлуулъя:

Хүлээн авсан үр дүнд тэгш байдлыг (2.1) нэмбэл бид:
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \баруун)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \баруун)"= 108\cdot\left(\arctg(4\cdot \ln x) \баруун)^(11)\cdot (\arctg(4\cdot \ln x))" \tag (2.2) $$
Ийм нөхцөлд шийдвэр гаргагч эхний алхамд томьёоны оронд $(\arctg \; u)"=\frac(1)(1+u^2)\cdot u"$ томьёог сонгоход алдаа гардаг. $\left(u^\ alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Гол нь гадаад функцийн дериватив хамгийн түрүүнд байх ёстой. $\arctg^(12)(4\cdot 5^x)$ илэрхийллийн гаднах функцийг ойлгохын тулд $\arctg^(12)(4\cdot 5^) илэрхийллийн утгыг тооцоолж байна гэж төсөөлөөд үз дээ. x)$ тодорхой хэмжээгээр $x$. Эхлээд та $5^x$-ийн утгыг тооцоолж, үр дүнг 4-өөр үржүүлж, $4\cdot 5^x$ авна. Одоо бид энэ үр дүнгээс арктангенсыг авч, $\arctg(4\cdot 5^x)$-г олж авна. Дараа нь бид гарсан тоог арван хоёр дахь зэрэглэлд хүргэж, $\arctg^(12)(4\cdot 5^x)$ авна. Сүүлийн үйлдэл, өөрөөр хэлбэл. 12-ын хүчийг нэмэгдүүлэх нь гадаад функц болно. Эндээс бид тэгш байдлын дагуу хийгдсэн деривативыг олж эхлэх ёстой (2.2).
Одоо бид $(\arctg(4\cdot \ln x))"$-г олох хэрэгтэй. Бид деривативын хүснэгтийн 19-р томьёог ашиглаж, $u=4\cdot \ln x$-г орлуулна:
$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)" $$
$(4\cdot \ln x)^2=4^2\cdot (\ln x)^2=16\cdot \ln^2 x$-г харгалзан үр дүнгийн илэрхийлэлийг бага зэрэг хялбарчилж үзье.
$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)"=\frac( 1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" $$
Тэгш байдал (2.2) одоо болно:
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \баруун)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \баруун)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" \tag (2.3) $$
$(4\cdot \ln x)"$-г олоход л үлдлээ. Дериватив тэмдгээс тогтмолыг (өөрөөр хэлбэл 4) гаргая: $(4\cdot \ln x)"=4\cdot (\ln x)" $. For $(\ln x)"$-г олохын тулд бид 8-р томьёог ашиглан $u=x$ гэж орлуулна: $(\ln x)"=\frac(1)(x)\cdot x "$. $x"=1$ тул $(\ln x)"=\frac(1)(x)\cdot x"=\frac(1)(x)\cdot 1=\frac(1)(x ) $ Хүлээн авсан үр дүнг (2.3) томъёонд орлуулснаар бид дараахь зүйлийг олж авна.
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \баруун)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \баруун)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" =\\ =108\cdot \left(\arctg(4\cdot \ln x) \баруун)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot 4\ cdot \frac(1)(x)=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x)).$ доллар
Сүүлчийн тэгшитгэлд бичсэн шиг нийлмэл функцийн дериватив нэг мөрөнд ихэвчлэн олддог гэдгийг сануулъя. Тиймээс стандарт тооцоо, хяналтын ажлыг бэлтгэхдээ шийдлийг нарийвчлан тайлбарлах шаардлагагүй болно.
Хариулт: $y"=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x))$.
Жишээ №3
$y=\sqrt(\sin^3(5\cdot9^x))$ функцийн $y"$-г ол.
Эхлээд $y$ функцийг бага зэрэг хувиргаж, радикал (үндэс)-ийг хүч болгон илэрхийлье: $y=\sqrt(\sin^3(5\cdot9^x))=\left(\sin(5\cdot 9) ^x) \right)^(\frac(3)(7))$. Одоо деривативыг хайж эхэлцгээе. $y=\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))$ тул:
$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\баруун)" \tag (3.1) $$
$u=\sin(5\cdot 9^x)$ болон $\alpha=\frac(3)(7)$-г орлуулж, деривативын хүснэгтээс 2-р томьёог ашиглая:
$$ \left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"= \frac(3)(7)\cdot \left( \sin(5\cdot 9^x)\right)^(\frac(3)(7)-1) (\sin(5\cdot 9^x))"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" $$
Хүлээн авсан үр дүнг ашиглан тэгш байдлыг (3.1) үргэлжлүүлье.
$$ y"=\left(\left(\sin(5\cdot 9^x)\баруун)^(\frac(3)(7))\баруун)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" \tag (3.2) $$
Одоо бид $(\sin(5\cdot 9^x))"$-г олох хэрэгтэй. Үүний тулд бид деривативын хүснэгтээс 9-р томьёог ашиглан $u=5\cdot 9^x$-г орлуулна.
$$ (\sin(5\cdot 9^x))"=\cos(5\cdot 9^x)\cdot(5\cdot 9^x)" $$
Хүлээн авсан үр дүнд тэгш байдлыг (3.2) нэмснээр бид дараахь зүйлийг олж авна.
$$ y"=\left(\left(\sin(5\cdot 9^x)\баруун)^(\frac(3)(7))\баруун)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9) ^x)" \tag (3.3) $$
$(5\cdot 9^x)"$-г олоход л үлдлээ. Эхлээд дериватив тэмдгийн гаднах тогтмолыг ($5$ тоо) авч үзье, өөрөөр хэлбэл $(5\cdot 9^x)"=5\cdot (9). ^x) "$. $(9^x)"$ деривативыг олохын тулд деривативын хүснэгтийн 5-р томьёог ашиглан $a=9$, $u=x$-ийг орлуулан: $(9^x) )"=9^x\cdot \ ln9\cdot x"$. $x"=1$ тул $(9^x)"=9^x\cdot \ln9\cdot x"=9^x\cdot \ln9$. Одоо бид тэгш байдлыг (3.3) үргэлжлүүлж болно:
$$ y"=\left(\left(\sin(5\cdot 9^x)\баруун)^(\frac(3)(7))\баруун)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9) ^x)"= \frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9 ^x)\cdot 5\cdot 9^x\cdot \ln9=\\ =\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\баруун) ^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x. $$
Бид $\left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))$-г $\ хэлбэрээр бичиж, хүчнээс радикалууд (жишээ нь, үндэс) рүү дахин буцаж болно. frac(1)(\left(\sin(5\cdot 9^x)\баруун)^(\frac(4)(7)))=\frac(1)(\sqrt(\sin^4(5\) cdot 9^x)))$. Дараа нь деривативыг дараах хэлбэрээр бичнэ.
$$ y"=\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x= \frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x) (\sqrt(\sin^4(5\cdot 9^x))).$$
Хариулт: $y"=\frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x)(\sqrt(\sin^4(5\) cdot 9^x)))$.
Жишээ № 4
Деривативын хүснэгтийн 3, 4-р томьёо нь энэ хүснэгтийн 2-р томьёоны онцгой тохиолдол болохыг харуул.
Деривативын хүснэгтийн 2-р томьёо нь $u^\alpha$ функцийн деривативыг агуулна. №2 томьёонд $\alpha=-1$-г орлуулснаар бид дараахыг авна.
$$(u^(-1))"=-1\cdot u^(-1-1)\cdot u"=-u^(-2)\cdot u"\tag (4.1)$$
$u^(-1)=\frac(1)(u)$ ба $u^(-2)=\frac(1)(u^2)$ тул тэгш байдлыг (4.1) дараах байдлаар дахин бичиж болно. $ \left(\frac(1)(u) \right)"=-\frac(1)(u^2)\cdot u"$. Энэ бол деривативын хүснэгтийн 3-р томъёо юм.
Деривативын хүснэгтийн 2-р томьёог дахин авч үзье. Үүнд $\alpha=\frac(1)(2)$ орлъё:
$$\left(u^(\frac(1)(2))\баруун)"=\frac(1)(2)\cdot u^(\frac(1)(2)-1)\cdot u" =\frac(1)(2)u^(-\frac(1)(2))\cdot u"\tag (4.2) $$
Учир нь $u^(\frac(1)(2))=\sqrt(u)$ ба $u^(-\frac(1)(2))=\frac(1)(u^(\frac( 1) )(2)))=\frac(1)(\sqrt(u))$, тэгш байдлыг (4.2) дараах байдлаар дахин бичиж болно.
$$ (\sqrt(u))"=\frac(1)(2)\cdot \frac(1)(\sqrt(u))\cdot u"=\frac(1)(2\sqrt(u) )\cdot u" $$
Үүссэн $(\sqrt(u))"=\frac(1)(2\sqrt(u))\cdot u"$ нь деривативын хүснэгтийн 4-р томьёо юм. Таны харж байгаагаар дериватив хүснэгтийн 3, 4-р томьёог 2-р томъёоноос харгалзах $\alpha$ утгыг орлуулах замаар олж авсан.
Математикийн физикийн асуудал эсвэл жишээг шийдвэрлэх нь дериватив, түүнийг тооцоолох аргуудын талаар мэдлэггүйгээр бүрэн боломжгүй юм. Дериватив нь математик шинжилгээний хамгийн чухал ойлголтуудын нэг юм. Бид өнөөдрийн нийтлэлийг энэ үндсэн сэдэвт зориулахаар шийдлээ. Дериватив гэж юу вэ, түүний физик, геометрийн утга нь юу вэ, функцийн деривативыг хэрхэн тооцоолох вэ? Эдгээр бүх асуултыг нэг дор нэгтгэж болно: деривативыг хэрхэн ойлгох вэ?
Деривативын геометрийн болон физикийн утга
Функц байх болтугай f(x) , тодорхой интервалд заасан (а, б) . x ба x0 цэгүүд энэ интервалд хамаарна. X өөрчлөгдөхөд функц нь өөрөө өөрчлөгддөг. Аргументыг өөрчлөх - түүний утгуудын ялгаа x-x0 . Энэ ялгааг дараах байдлаар бичнэ дельта х ба аргументийн өсөлт гэж нэрлэдэг. Функцийн өөрчлөлт эсвэл өсөлт нь хоёр цэг дэх функцийн утгуудын зөрүү юм. Деривативын тодорхойлолт:
Тухайн цэг дэх функцийн үүсмэл утга нь өгөгдсөн цэг дэх функцийн өсөлтийг аргументийн өсөлттэй харьцуулсан харьцааны хязгаар нь тэг байх хандлагатай байдаг.
Үгүй бол дараах байдлаар бичиж болно.

Ийм хязгаар олох нь ямар учиртай юм бэ? Тэгээд энэ нь юу вэ:
цэг дээрх функцийн дериватив нь OX тэнхлэг хоорондын өнцгийн тангенс ба тухайн цэг дэх функцийн графиктай шүргэгчтэй тэнцүү байна.

Деривативын физик утга: цаг хугацааны хувьд замын дериватив нь шулуун хөдөлгөөний хурдтай тэнцүү байна.
Сургуулийн наснаас хойш хүн бүр хурд бол тодорхой зам гэдгийг мэддэг x=f(t) ба цаг хугацаа т . Тодорхой хугацааны дундаж хурд:

Цаг мөчид хөдөлгөөний хурдыг олж мэдэх t0 Та хязгаарыг тооцоолох хэрэгтэй:

Нэгдүгээр дүрэм: тогтмолыг тохируулах
Тогтмолыг дериватив тэмдгээс гаргаж авч болно. Түүнээс гадна үүнийг хийх ёстой. Математикийн жишээг шийдвэрлэхдээ үүнийг дүрмээр аваарай - Хэрэв та илэрхийлэлийг хялбарчилж чадвал түүнийг хялбарчлахаа мартуузай .
Жишээ. Деривативыг тооцоолъё:

Хоёрдугаар дүрэм: функцүүдийн нийлбэрийн дериватив
Хоёр функцийн нийлбэрийн дериватив нь эдгээр функцүүдийн деривативуудын нийлбэртэй тэнцүү байна. Функцийн зөрүүний деривативын хувьд ч мөн адил.

Бид энэ теоремын баталгааг өгөхгүй, харин практик жишээг авч үзэх болно.
Функцийн деривативыг ол:


Гуравдугаар дүрэм: функцүүдийн үржвэрийн дериватив
Хоёр дифференциалагдах функцийн үржвэрийн деривативыг дараах томъёогоор тооцоолно.

Жишээ нь: функцийн деривативыг ол:

Шийдэл: 
Энд нарийн төвөгтэй функцүүдийн деривативыг тооцоолох талаар ярих нь чухал юм. Комплекс функцийн дериватив нь завсрын аргументтай харьцуулахад энэ функцийн деривативын үржвэртэй, бие даасан хувьсагчийн хувьд завсрын аргументийн деривативтай тэнцүү байна.
Дээрх жишээн дээр бид дараах илэрхийлэлтэй тулгардаг.

Энэ тохиолдолд завсрын аргумент нь тав дахь зэрэглэлд 8x байна. Ийм илэрхийллийн деривативыг тооцоолохын тулд эхлээд завсрын аргументтай холбоотойгоор гадаад функцийн деривативыг тооцож, дараа нь бие даасан хувьсагчийн хувьд завсрын аргументийн деривативаар үржүүлнэ.
Дөрөвдүгээр дүрэм: хоёр функцийн хуваалтын дериватив
Хоёр функцийн хуваалтын деривативыг тодорхойлох томъёо:



Бид даммигийн деривативын талаар эхнээс нь ярихыг хичээсэн. Энэ сэдэв нь тийм ч энгийн зүйл биш тул анхааруулах хэрэгтэй: жишээнүүдэд алдаанууд ихэвчлэн байдаг тул деривативыг тооцоолохдоо болгоомжтой байгаарай.
Энэ болон бусад сэдвээр асуух зүйл байвал оюутны үйлчилгээтэй холбогдож болно. Богино хугацаанд бид танд хамгийн хэцүү сорилтыг шийдэж, даалгавруудыг ойлгоход тань туслах болно, тэр ч байтугай та урьд өмнө хэзээ ч дериватив тооцоо хийж байгаагүй.
Хэрэв та тодорхойлолтыг дагаж мөрдвөл тухайн цэг дэх функцийн дериватив нь Δ функцийн өсөлтийн харьцааны хязгаар юм. yаргументийн өсөлт рүү Δ x:
Бүх зүйл ойлгомжтой байх шиг байна. Гэхдээ энэ томъёог ашиглан функцийн деривативыг тооцоолж үзээрэй е(x) = x 2 + (2x+ 3) · д xнүгэл x. Хэрэв та бүх зүйлийг тодорхойлолтоор хийвэл хэдэн хуудас тооцоо хийсний дараа та зүгээр л унтах болно. Тиймээс илүү энгийн бөгөөд үр дүнтэй аргууд байдаг.
Эхлэхийн тулд бид бүх төрлийн функцүүдээс энгийн функц гэж нэрлэгддэг функцүүдийг ялгаж салгаж болно гэдгийг тэмдэглэж байна. Эдгээр нь харьцангуй энгийн илэрхийллүүд бөгөөд деривативуудыг удаан хугацаанд тооцоолж, хүснэгтэд оруулав. Ийм функцууд нь тэдгээрийн деривативуудын хамт санахад хялбар байдаг.
Энгийн функцүүдийн деривативууд
Үндсэн функцууд нь доор жагсаасан бүх функцууд юм. Эдгээр функцүүдийн деривативуудыг цээжээр мэддэг байх ёстой. Түүнээс гадна тэдгээрийг цээжлэх нь тийм ч хэцүү биш - тиймээс тэд анхан шатны шинж чанартай байдаг.
Тиймээс, үндсэн функцүүдийн деривативууд:
| Нэр | Чиг үүрэг | Дериватив |
| Тогтмол | е(x) = C, C ∈ Р | 0 (тийм ээ, тэг!) |
| Рационал үзүүлэлттэй хүч | е(x) = x n | n · x n − 1 |
| Синус | е(x) = нүгэл x | cos x |
| Косинус | е(x) = cos x | - нүгэл x(хасах синус) |
| Тангенс | е(x) = тг x | 1/cos 2 x |
| Котангенс | е(x) = ctg x | − 1/нүгэл 2 x |
| Байгалийн логарифм | е(x) = бүртгэл x | 1/x |
| Дурын логарифм | е(x) = бүртгэл а x | 1/(x ln а) |
| Экспоненциал функц | е(x) = д x | д x(юу ч өөрчлөгдөөгүй) |
Хэрэв энгийн функцийг дурын тогтмол тоогоор үржүүлбэл шинэ функцийн деривативыг хялбархан тооцоолно.
(C · е)’ = C · е ’.
Ерөнхийдөө деривативын тэмдгээс тогтмолуудыг авч болно. Жишээлбэл:
(2x 3)’ = 2 · ( x 3)’ = 2 3 x 2 = 6x 2 .
Мэдээжийн хэрэг, энгийн функцуудыг бие биендээ нэмэх, үржүүлэх, хуваах гэх мэт олон зүйлийг хийх боломжтой. Ийм байдлаар шинэ функцууд гарч ирэх бөгөөд энэ нь ялангуяа энгийн байхаа больсон боловч тодорхой дүрмийн дагуу ялгаатай байх болно. Эдгээр дүрмийг доор авч үзэх болно.
Нийлбэр ба зөрүүний дериватив
Функцуудыг өгье е(x) Мөн g(x), деривативууд нь бидэнд мэдэгддэг. Жишээлбэл, та дээр дурдсан үндсэн функцуудыг авч болно. Дараа нь та эдгээр функцүүдийн нийлбэр ба ялгааны деривативыг олох боломжтой.
- (е + g)’ = е ’ + g ’
- (е − g)’ = е ’ − g ’
Тэгэхээр хоёр функцийн нийлбэр (ялгаа) нь деривативуудын нийлбэр (ялгаа)-тай тэнцүү байна. Илүү олон нэр томъёо байж болно. Жишээлбэл, ( е + g + h)’ = е ’ + g ’ + h ’.
Хатуухан хэлэхэд алгебрт "хасах" гэсэн ойлголт байдаггүй. "Сөрөг элемент" гэсэн ойлголт байдаг. Тиймээс ялгаа е − gнийлбэр болгон дахин бичиж болно е+ (−1) g, дараа нь зөвхөн нэг томъёо үлдэнэ - нийлбэрийн дериватив.
е(x) = x 2 + нүгэл х; g(x) = x 4 + 2x 2 − 3.
Чиг үүрэг е(x) нь хоёр үндсэн функцийн нийлбэр тул:
е ’(x) = (x 2 + нүгэл x)’ = (x 2)' + (нүгэл x)’ = 2x+ cos x;
Бид функцийг ижил төстэй шалтгаанаар тайлбарладаг g(x). Зөвхөн гурван нэр томъёо байдаг (алгебрийн үүднээс):
g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).
Хариулт:
е ’(x) = 2x+ cos x;
g ’(x) = 4x · ( x
2 + 1).
Бүтээгдэхүүний дериватив
Математик бол логик шинжлэх ухаан тул олон хүн нийлбэрийн дериватив нь деривативын нийлбэртэй тэнцүү бол тухайн бүтээгдэхүүний дериватив гэж олон хүн үздэг. ажил хаях"> деривативын үржвэртэй тэнцүү байна. Гэхдээ та эргэлзээрэй! Бүтээгдэхүүний деривативыг огт өөр томъёогоор тооцдог. Тухайлбал:
(е · g) ’ = е ’ · g + е · g ’
Томъёо нь энгийн боловч ихэнхдээ мартагддаг. Зөвхөн сургуулийн сурагчид төдийгүй оюутнууд ч гэсэн. Үр дүн нь буруу шийдэгдсэн асуудлууд юм.
Даалгавар. Функцийн деривативыг ол: е(x) = x 3 cos x; g(x) = (x 2 + 7x− 7) · д x .
Чиг үүрэг е(x) нь хоёр үндсэн функцын бүтээгдэхүүн тул бүх зүйл энгийн:
е ’(x) = (x 3 cos x)’ = (x 3)’ cos x + x 3 (cos x)’ = 3x 2 cos x + x 3 (− нүгэл x) = x 2 (3cos x − xнүгэл x)
Чиг үүрэг g(x) эхний үржүүлэгч нь арай илүү төвөгтэй боловч ерөнхий схем өөрчлөгддөггүй. Мэдээжийн хэрэг, функцийн эхний хүчин зүйл g(x) нь олон гишүүнт ба дериватив нь нийлбэрийн дериватив юм. Бидэнд байгаа:
g ’(x) = ((x 2 + 7x− 7) · д x)’ = (x 2 + 7x− 7)’ · д x + (x 2 + 7x− 7) · ( д x)’ = (2x+ 7) · д x + (x 2 + 7x− 7) · д x = д x· (2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · д x = x(x+ 9) · д x .
Хариулт:
е ’(x) = x 2 (3cos x − xнүгэл x);
g ’(x) = x(x+ 9) · д
x
.
Сүүлийн шатанд деривативыг хүчин зүйлээр ангилдаг болохыг анхаарна уу. Албан ёсоор үүнийг хийх шаардлагагүй, гэхдээ ихэнх деривативуудыг дангаар нь тооцдоггүй, харин функцийг шалгахын тулд хийдэг. Энэ нь цаашид деривативыг тэгтэй тэнцүүлэх, түүний тэмдгүүдийг тодорхойлох гэх мэт болно гэсэн үг юм. Ийм тохиолдолд илэрхийлэлийг хүчин зүйл болгон хуваах нь дээр.
Хэрэв хоёр функц байгаа бол е(x) Мөн g(x), болон g(x) Бидний сонирхож буй олонлог дээр ≠ 0 байвал бид шинэ функцийг тодорхойлж болно h(x) = е(x)/g(x). Ийм функцийн хувьд та деривативыг олж болно:
Сул биш, тийм үү? Хасах нь хаанаас ирсэн бэ? Яагаад g 2? Мөн үүн шиг! Энэ бол хамгийн төвөгтэй томъёонуудын нэг бөгөөд та үүнийг лонхгүйгээр олж чадахгүй. Тиймээс үүнийг тодорхой жишээн дээр судлах нь дээр.
Даалгавар. Функцийн деривативыг ол:
Бутархай тус бүрийн тоологч ба хуваагч нь энгийн функцуудыг агуулдаг тул бидэнд хэрэгтэй зүйл бол энэ хэсгийн деривативын томъёо юм.
Уламжлал ёсоор тоологчийг хүчин зүйл болгон хувацгаая - энэ нь хариултыг ихээхэн хялбаршуулах болно:
Нарийн төвөгтэй функц нь хагас километрийн урттай томьёо байх албагүй. Жишээлбэл, функцийг авахад хангалттай е(x) = нүгэл xболон хувьсагчийг солино x, дээр гэж хэлье x 2 + лн x. Энэ нь бүтэх болно е(x) = нүгэл ( x 2 + лн x) - энэ бол нарийн төвөгтэй функц юм. Энэ нь мөн деривативтай боловч дээр дурдсан дүрмийн дагуу үүнийг олох боломжгүй болно.
Би юу хийх хэрэгтэй вэ? Ийм тохиолдолд нийлмэл функцийн деривативын хувьсагч болон томъёог орлуулах нь дараахь зүйлийг хийхэд тусална.
е ’(x) = е ’(т) · т', Хэрэв x-ээр солигдоно т(x).
Дүрмээр бол, энэ томъёог ойлгох нөхцөл байдал нь квентийн деривативаас ч илүү гунигтай байдаг. Тиймээс үүнийг тодорхой жишээн дээр тайлбарлах нь дээр Дэлгэрэнгүй тодорхойлолталхам бүр.
Даалгавар. Функцийн деривативыг ол: е(x) = д 2x + 3 ; g(x) = нүгэл ( x 2 + лн x)
Хэрэв функцэд байгаа бол гэдгийг анхаарна уу е(x) илэрхийлэл 2-ын оронд x+ 3 амархан байх болно x, дараа нь бид энгийн функцийг авна е(x) = д x. Тиймээс, бид орлуулалт хийдэг: 2-ыг зөвшөөрье x + 3 = т, е(x) = е(т) = д т. Бид нийлмэл функцийн деривативыг дараах томъёогоор хайдаг.
е ’(x) = е ’(т) · т ’ = (д т)’ · т ’ = д т · т ’
Тэгээд одоо - анхаарлаа хандуулаарай! Бид урвуу орлуулалтыг гүйцэтгэдэг: т = 2x+ 3. Бид дараахыг авна:
е ’(x) = д т · т ’ = д 2x+ 3 (2 x + 3)’ = д 2x+ 3 2 = 2 д 2x + 3
Одоо функцийг харцгаая g(x). Үүнийг солих шаардлагатай нь ойлгомжтой x 2 + лн x = т. Бидэнд байгаа:
g ’(x) = g ’(т) · т' = (нүгэл т)’ · т’ = cos т · т ’
Урвуу солих: т = x 2 + лн x. Дараа нь:
g ’(x) = cos ( x 2 + лн x) · ( x 2 + лн x)’ = cos ( x 2 + лн x) · (2 x + 1/x).
Тэгээд л болоо! Сүүлийн илэрхийллээс харахад бүх асуудлыг үүсмэл нийлбэрийг тооцоолох хүртэл багасгасан.
Хариулт:
е ’(x) = 2 · д
2x + 3 ;
g ’(x) = (2x + 1/x) учир нь ( x 2 + лн x).
Хичээлдээ би "үүсмэл" гэсэн нэр томъёоны оронд "анхны" гэдэг үгийг ихэвчлэн ашигладаг. Жишээлбэл, нийлбэрийн цохилт нь цус харвалтын нийлбэртэй тэнцүү байна. Энэ нь илүү ойлгомжтой юу? За, сайн байна.
Тиймээс деривативыг тооцоолох нь дээр дурдсан дүрмийн дагуу эдгээр ижил цохилтоос ангижрахад хүргэдэг. Эцсийн жишээ болгон рационал илтгэгчтэй дериватив хүчин рүү буцъя:
(x n)’ = n · x n − 1
Цөөхөн хүн дүрд нь үүнийг мэддэг nбутархай тоо байж магадгүй. Жишээлбэл, үндэс нь x 0.5. Үндэс дор нь ямар нэгэн гоёмсог зүйл байвал яах вэ? Дахин хэлэхэд үр дүн нь нарийн төвөгтэй функц байх болно - тэд ийм барилга байгууламжийг өгөх дуртай туршилтуудболон шалгалтууд.
Даалгавар. Функцийн деривативыг ол:
Эхлээд язгуурыг рационал илтгэгчтэй зэрэглэлээр дахин бичье.
е(x) = (x 2 + 8x − 7) 0,5 .
Одоо бид орлуулалт хийж байна: зөвшөөрөх x 2 + 8x − 7 = т. Бид дараах томъёог ашиглан деривативыг олно.
е ’(x) = е ’(т) · т ’ = (т 0.5)’ · т’ = 0.5 · т−0.5 · т ’.
Урвуу орлуулалтыг хийцгээе: т = x 2 + 8x− 7. Бидэнд:
е ’(x) = 0.5 · ( x 2 + 8x− 7) −0.5 · ( x 2 + 8x− 7)’ = 0.5 · (2 x+ 8) ( x 2 + 8x − 7) −0,5 .
Эцэст нь, үндэс рүү буцах:
Санахад маш амархан.
За, хол явахгүй, шууд харцгаая урвуу функц. Аль функц нь экспоненциал функцийн урвуу функц вэ? Логарифм:
Манай тохиолдолд суурь нь дараах тоо юм.
Ийм логарифмийг (өөрөөр хэлбэл суурьтай логарифм) "байгалийн" гэж нэрлэдэг бөгөөд бид үүнд зориулж тусгай тэмдэглэгээ ашигладаг: бид оронд нь бичдэг.
Энэ нь юутай тэнцүү вэ? Мэдээжийн хэрэг, .
Байгалийн логарифмын дериватив нь маш энгийн:
Жишээ нь:
- Функцийн деривативыг ол.
- Функцийн дериватив нь юу вэ?
Хариултууд: Экспоненциал ба натурал логарифм нь дериватив талаас нь авч үзвэл маш энгийн функцууд юм. Бусад суурьтай экспоненциал болон логарифм функцууд нь өөр деривативтай байх бөгөөд бид үүнийг ялгах дүрмийн дагуу дараа нь шинжлэх болно.
Ялгах дүрэм
Юуны дүрэм? Ахиад л шинэ нэр томъёо, дахиад?!...
Ялгаварлахдеривативыг олох үйл явц юм.
Тэгээд л болоо. Энэ үйл явцыг нэг үгээр өөр юу гэж нэрлэх вэ? Дериватив биш ... Математикчид дифференциалыг функцийн ижил өсөлт гэж нэрлэдэг. Энэ нэр томъёо нь Латин дифференциас - ялгаа гэсэн үгнээс гаралтай. Энд.
Эдгээр бүх дүрмийг гаргахдаа бид хоёр функцийг ашиглана, жишээ нь, ба. Бидэнд мөн тэдгээрийн өсөлтийн томъёо хэрэгтэй болно:
Нийтдээ 5 дүрэм байдаг.
Тогтмолыг дериватив тэмдгээс хасна.
Хэрэв - зарим тогтмол тоо (тогтмол), дараа нь.
Мэдээжийн хэрэг, энэ дүрэм нь ялгааны хувьд бас ажилладаг: .
Үүнийг баталъя. Байг, эсвэл илүү энгийн.
Жишээ.
Функцийн деривативуудыг ол:
- нэг цэг дээр;
- нэг цэг дээр;
- нэг цэг дээр;
- цэг дээр.
Шийдэл:
- (Үүсвэр нь бүх цэгт ижил байна, учир нь үүнээс хойш шугаман функц, санаж байна уу?);
Бүтээгдэхүүний дериватив
Энд бүх зүйл ижил байна: шинэ функцийг нэвтрүүлж, түүний өсөлтийг олцгооё:
Дериватив:
Жишээ нь:
- Функцийн деривативыг олох ба;
- Тухайн цэг дээрх функцийн деривативыг ол.
Шийдэл:
Экспоненциал функцийн дериватив
Одоо таны мэдлэг зөвхөн экспоненциал функцийн деривативыг хэрхэн олохыг сурахад хангалттай юм (энэ нь юу болохыг та мартаагүй байна уу?).
Тэгэхээр хэдэн тоо хаана байна.
Бид функцийн деривативыг аль хэдийн мэдэж байгаа тул функцээ шинэ суурь болгон багасгахыг хичээцгээе.
Үүнийг хийхийн тулд бид энгийн дүрмийг ашиглах болно: . Дараа нь:
За, энэ ажилласан. Одоо деривативыг олохыг хичээ, энэ функц нь нарийн төвөгтэй гэдгийг мартаж болохгүй.
Болсон уу?
Энд өөрийгөө шалгаарай:
Томъёо нь экспонентийн деривативтай маш төстэй болж хувирав: энэ нь хэвээр үлдэж, зөвхөн нэг хүчин зүйл гарч ирсэн бөгөөд энэ нь зүгээр л тоо боловч хувьсагч биш юм.
Жишээ нь:
Функцийн деривативуудыг ол:
Хариултууд:
Энэ бол зүгээр л тооны машингүйгээр тооцоолох боломжгүй, өөрөөр хэлбэл үүнийг цаашид бичих боломжгүй тоо юм. энгийн хэлбэрээр. Тиймээс бид үүнийг хариултдаа энэ хэлбэрээр үлдээж байна.
Энд хоёр функцийн коэффициент байгааг анхаарна уу, тиймээс бид харгалзах ялгах дүрмийг хэрэглэнэ.
Энэ жишээнд хоёр функцийн үржвэр:
Логарифм функцийн дериватив
Үүнтэй төстэй: та байгалийн логарифмын деривативыг аль хэдийн мэддэг болсон.
Тиймээс өөр суурьтай дурын логарифмийг олохын тулд, жишээлбэл:
Бид энэ логарифмыг суурь болгон багасгах хэрэгтэй. Логарифмын суурийг хэрхэн өөрчлөх вэ? Та энэ томъёог санаж байна гэж найдаж байна:
Зөвхөн одоо бид оронд нь бичих болно:
Хуваагч нь зүгээр л тогтмол (хувьсагчгүй тогтмол тоо) юм. Деривативыг маш энгийнээр олж авдаг:
Экспоненциал ба логарифм функцийн деривативууд нь Улсын нэгдсэн шалгалтанд бараг хэзээ ч олддоггүй, гэхдээ тэдгээрийг мэдэх нь илүүц байх болно.
Нарийн төвөгтэй функцийн дериватив.
"Цогцолбор функц" гэж юу вэ? Үгүй ээ, энэ бол логарифм биш, арктангенс ч биш. Эдгээр функцийг ойлгоход хэцүү байж болох юм (хэдийгээр танд логарифм хийхэд хэцүү гэж үзвэл "Логарифм" гэсэн сэдвийг уншвал зүгээр байх болно), гэхдээ математикийн үүднээс "цогцолбор" гэдэг нь "хэцүү" гэсэн үг биш юм.
Жижиг туузан дамжуулагчийг төсөөлөөд үз дээ: хоёр хүн сууж, зарим объекттой зарим үйлдэл хийж байна. Жишээлбэл, эхнийх нь шоколадны баарыг боодол дээр боож, хоёр дахь нь туузаар холбодог. Үр дүн нь нийлмэл объект юм: шоколадны баар ороож, туузаар холбосон. Шоколадны баар идэхийн тулд урвуу дарааллаар урвуу алхмуудыг хийх хэрэгтэй.
Үүнтэй төстэй математик шугамыг бүтээцгээе: эхлээд бид тооны косинусыг олж, дараа нь гарсан тоог квадрат болгоно. Тиймээс, бидэнд тоо (шоколад) өгөгдсөн, би түүний косинусыг (боодол) олоод, дараа нь та миний авсан зүйлийг дөрвөлжин болго (туузаар уя). Юу болсон бэ? Чиг үүрэг. Энэ бол нарийн төвөгтэй функцийн жишээ юм: утгыг олохын тулд бид эхний үйлдлийг хувьсагчтай шууд хийж, дараа нь эхний үйлдлээс үүссэн хоёр дахь үйлдлийг гүйцэтгэдэг.
Өөрөөр хэлбэл, нийлмэл функц нь аргумент нь өөр функц болох функц юм: .
Бидний жишээн дээр, .
Бид урвуу дарааллаар ижил алхмуудыг хялбархан хийж чадна: эхлээд та үүнийг квадрат болго, дараа нь би гарсан тооны косинусыг хайна: . Үр дүн нь бараг үргэлж өөр байх болно гэдгийг таахад хялбар байдаг. Нарийн төвөгтэй функцүүдийн чухал шинж чанар: үйлдлийн дараалал өөрчлөгдөхөд функц өөрчлөгддөг.
Хоёр дахь жишээ: (ижил зүйл). .
Бидний хамгийн сүүлд хийх үйлдлийг дуудах болно "гадаад" функц, мөн хамгийн түрүүнд гүйцэтгэсэн үйлдэл - үүний дагуу "дотоод" функц(эдгээр нь албан бус нэрс, би зөвхөн материалыг энгийн хэлээр тайлбарлахад ашигладаг).
Аль функц нь гадаад, аль нь дотоод гэдгийг өөрөө тодорхойлохыг хичээ.
Хариултууд:Дотоод болон гадаад функцийг салгах нь хувьсагчийг өөрчлөхтэй маш төстэй: жишээлбэл, функцэд
- Бид хамгийн түрүүнд ямар үйлдэл хийх вэ? Эхлээд синусыг тооцоод дараа нь шоо болгоё. Энэ нь дотоод функц, гэхдээ гадаад функц гэсэн үг юм.
Мөн анхны функц нь тэдний найрлага юм: . - Дотоод: ; гадна: .
Шалгалт: . - Дотоод: ; гадна: .
Шалгалт: . - Дотоод: ; гадна: .
Шалгалт: . - Дотоод: ; гадна: .
Шалгалт: .
Бид хувьсагчдыг өөрчилж, функцийг авдаг.
За, одоо бид шоколадаа гаргаж аваад деривативыг хайх болно. Процедур нь үргэлж эсрэгээрээ байдаг: эхлээд бид гадаад функцийн деривативыг хайж, дараа нь үр дүнг дотоод функцийн деривативаар үржүүлнэ. Анхны жишээтэй холбоотойгоор дараах байдалтай байна.
Өөр нэг жишээ:
Ингээд эцэст нь албан ёсны дүрмийг томъёолъё:
Нарийн төвөгтэй функцийн деривативыг олох алгоритм:
Энэ нь энгийн юм шиг санагдаж байна, тийм үү?
Жишээнүүдээр шалгацгаая:
Шийдэл:
1) Дотоод: ;
Гадна: ;
2) Дотоод: ;
(Одоогоор таслах гэж бүү оролдоорой! Косинусын доороос юу ч гарахгүй, санаж байна уу?)
3) Дотоод: ;
Гадна: ;
Энэ нь гурван түвшний нарийн төвөгтэй функц болох нь шууд тодорхой байна: эцэст нь энэ нь өөрөө нарийн төвөгтэй функц бөгөөд бид үүнээс үндсийг нь гаргаж авдаг, өөрөөр хэлбэл бид гурав дахь үйлдлийг гүйцэтгэдэг (шоколадыг боодол дээр хийнэ) мөн цүнхэнд туузтай). Гэхдээ айх шалтгаан байхгүй: бид энэ функцийг ердийнх шигээ дарааллаар нь "тайлах" болно: эцсээс нь.
Өөрөөр хэлбэл, бид эхлээд үндсийг, дараа нь косинусыг, дараа нь хаалтанд байгаа илэрхийлэлийг ялгадаг. Тэгээд бид бүгдийг үржүүлнэ.
Ийм тохиолдолд үйлдлүүдийг дугаарлах нь тохиромжтой. Энэ нь юу мэддэгээ төсөөлөөд үз дээ. Энэ илэрхийллийн утгыг тооцоолох үйлдлийг бид ямар дарааллаар гүйцэтгэх вэ? Нэг жишээг харцгаая:
Үйлдлийг хожим гүйцэтгэх тусам харгалзах функц нь "гадаад" байх болно. Үйлдлүүдийн дараалал нь өмнөхтэй адил байна:
Энд үүрлэх нь ерөнхийдөө 4 түвшинтэй байдаг. Үйл ажиллагааны чиглэлийг тодорхойлъё.
1. Радикал илэрхийлэл. .
2. Үндэс. .
3. Синус. .
4. Дөрвөлжин. .
5. Бүгдийг нэгтгэх нь:
ҮҮСГЭЛ. ГОЛ ЗҮЙЛИЙН ТУХАЙ ТОВЧХОН
Функцийн дериватив- функцийн өсөлтийг аргументийн хязгааргүй бага өсөлтийн аргументийн өсөлттэй харьцуулсан харьцаа:
Үндсэн деривативууд:
Ялгах дүрэм:
Тогтмолыг дериватив тэмдгээс хасна:
Нийлбэрийн дериватив:
Бүтээгдэхүүний дериватив:
Хэсгийн дериватив:
Нарийн төвөгтэй функцийн дериватив:
Нарийн төвөгтэй функцийн деривативыг олох алгоритм:
- Бид "дотоод" функцийг тодорхойлж, түүний уламжлалыг олдог.
- Бид "гадаад" функцийг тодорхойлж, түүний уламжлалыг олдог.
- Бид эхний болон хоёр дахь цэгүүдийн үр дүнг үржүүлдэг.
Та энд ирснээс хойш сурах бичигт энэ томъёог аль хэдийн харсан байх
мөн ийм царай гарга:
Найз минь, санаа зовох хэрэггүй! Үнэн хэрэгтээ бүх зүйл зүгээр л жигшүүртэй байдаг. Та бүх зүйлийг мэдээж ойлгох болно. Зөвхөн нэг хүсэлт - нийтлэлийг уншина уу аажмаар, алхам бүрийг ойлгохыг хичээ. Би аль болох энгийн бөгөөд ойлгомжтой бичсэн боловч та санааг ойлгох хэрэгтэй. Мөн нийтлэл дэх даалгавруудыг шийдвэрлэхээ мартуузай.
Нарийн төвөгтэй функц гэж юу вэ?
Та өөр орон сууц руу нүүж, том хайрцагт юм хийж байна гэж төсөөлөөд үз дээ. Сургуулийн бичгийн хэрэглүүр гэх мэт жижиг зүйлсийг цуглуулах хэрэгтэй гэж бодъё. Хэрэв та тэдгээрийг зүгээр л том хайрцагт хийвэл тэд бусад зүйлсийн дунд алга болно. Үүнээс зайлсхийхийн тулд та эхлээд уутанд хийж, дараа нь том хайрцагт хийж, дараа нь битүүмжилнэ. Энэхүү "цогцолбор" үйл явцыг доорх диаграммд үзүүлэв.

Математик үүнд ямар хамаатай юм шиг санагдаж байна? Тийм ээ, нарийн төвөгтэй функц нь яг ИТГЭЛ байдлаар үүсдэг ч гэсэн! Гагцхүү бид дэвтэр, үзэг биш \(x\) “баглаа” байхад “багц” болон “хайрцаг” нь өөр.
Жишээлбэл, x-г аваад үүнийг функц болгон "багц" болгоё:

Үүний үр дүнд бид мэдээж \(\cosx\) авна. Энэ бол бидний "цүнх" юм. Одоо үүнийг "хайрцаг" дотор хийцгээе - жишээлбэл, куб функц болгон багцлаарай.

Эцсийн эцэст юу болох вэ? Тийм ээ, "хайрцагт юмны уут", өөрөөр хэлбэл "X кубын косинус" байх болно.

Үүссэн загвар нь нарийн төвөгтэй функц юм. Энэ нь энгийн зүйлээс ялгаатай Хэд хэдэн "нөлөөллийг" (багц) нэг X дээр дараалан хэрэглэнэЭнэ нь "функцоос функц" - "сав баглаа боодол доторх савлагаа" юм шиг харагдаж байна.
Сургуулийн курст эдгээр "багц" маш цөөхөн төрөл байдаг бөгөөд ердөө дөрөв нь:

Одоо X-ийг эхлээд 7 суурьтай экспоненциал функц, дараа нь тригонометрийн функц болгон "багцгая". Бид авах:
\(x → 7^x → tg(7^x)\)
Одоо X-г хоёр удаа "багцгааж" үзье тригонометрийн функцууд, эхлээд , дараа нь:
\(x → sinx → cotg (sinx)\)
Энгийн, тийм үү?
Одоо функцүүдийг өөрөө бичээрэй, энд x:
- эхлээд косинус, дараа нь \(3\) суурьтай экспоненциал функцэд "багагддаг";
- эхлээд тав дахь зэрэглэлд, дараа нь шүргэгч рүү;
- эхлээд суурийн логарифм хүртэл \(4\)
, дараа нь \(-2\) руу очно.
Энэ даалгаврын хариултыг өгүүллийн төгсгөлд олоорой.
Бид X-ийг хоёр биш, гурван удаа "баглаж" чадах уу? Асуудалгүй! Мөн дөрөв, тав, хорин таван удаа. Жишээлбэл, x нь \(4\) удаа "савласан" функц байна:
\(y=5^(\log_2(\sin(x^4)))\)
Гэхдээ сургуулийн практикт ийм томъёо олдохгүй (оюутнууд илүү азтай байдаг - тэднийх илүү төвөгтэй байж магадгүй юм☺).
Нарийн төвөгтэй функцийг " задлах "
Өмнөх функцийг дахин харна уу. Та "савлах" дарааллыг олж чадах уу? Эхлээд юунд X чихэв, дараа нь юу гэх мэтээр эцсээ хүртэл. Өөрөөр хэлбэл, аль функц аль дотор нь үүрлэсэн бэ? Нэг хуудас цаас аваад юу гэж бодож байгаагаа бич. Та үүнийг дээр дурдсан сумтай гинжээр эсвэл өөр аргаар хийж болно.
Одоо зөв хариулт нь: эхлээд x-ийг \(4\)-р түвшинд "савласан", дараа нь үр дүнг синус болгон багцалж, улмаар \(2\) суурийн логарифмд байрлуулсан. , эцэст нь энэ бүхэл бүтэн бүтээн байгуулалтыг хүчирхэг тав болгон дүүргэв.
Өөрөөр хэлбэл та урвуу дарааллаар дарааллыг тайлах хэрэгтэй. Үүнийг хэрхэн хялбархан хийх талаар зөвлөгөө энд байна: нэн даруй X-г хараарай - та үүнээс бүжиглэх хэрэгтэй. Хэд хэдэн жишээг харцгаая.
Жишээлбэл, дараах функц байна: \(y=tg(\log_2x)\). Бид X-г хардаг - эхлээд юу болох вэ? Түүнээс авсан. Тэгээд? Үр дүнгийн тангенсыг авна. Дараалал нь ижил байх болно:
\(x → \log_2x → tg(\log_2x)\)
Өөр нэг жишээ: \(y=\cos((x^3))\). Шинжилгээ хийцгээе - эхлээд бид X-ийг куб болгож, дараа нь үр дүнгийн косинусыг авав. Энэ нь дараалал нь: \(x → x^3 → \cos((x^3))\). Анхаарна уу, функц нь эхнийхтэй төстэй юм шиг байна (зурагтай газар). Гэхдээ энэ нь огт өөр функц юм: энд шоо дотор x (өөрөөр хэлбэл, \(\cos((x·x·x)))\), харин шоо дотор косинус \(x\) байна ( өөрөөр хэлбэл, \(\cos x·\cosx·\cosx\)). Энэ ялгаа нь янз бүрийн "савлах" дарааллаас үүсдэг.
Сүүлийн жишээ (үндсэн чухал мэдээлэлтэй): \(y=\sin((2x+5))\). Тэд энд эхлээд юу хийсэн нь ойлгомжтой арифметик үйлдлүүд x-тэй, дараа нь үр дүнгийн синусыг авсан: \(x → 2x+5 → \sin((2x+5))\). Бөгөөд энэ нь чухал цэг: Хэдийгээр арифметик үйлдлүүд нь өөрөө функц биш боловч энд тэд мөн "баглаа боодлын" үүрэг гүйцэтгэдэг. Энэ нарийн чанарыг бага зэрэг гүнзгийрүүлье.
Дээр хэлсэнчлэн энгийн функцүүдэд x нэг удаа "багагддаг", нарийн төвөгтэй функцүүдэд хоёр ба түүнээс дээш байдаг. Түүнээс гадна энгийн функцүүдийн аливаа хослол (өөрөөр хэлбэл тэдгээрийн нийлбэр, зөрүү, үржүүлэх, хуваах) нь мөн адил юм. энгийн функц. Жишээлбэл, \(x^7\) нь энгийн функц бөгөөд \(ctg x\) мөн адил. Энэ нь тэдгээрийн бүх хослолууд нь энгийн функцууд гэсэн үг юм:
\(x^7+ ctg x\) - энгийн,
\(x^7· ор х\) – энгийн,
\(\frac(x^7)(ctg x)\) – энгийн гэх мэт.
Гэсэн хэдий ч, хэрэв ийм хослолд өөр нэг функц ашиглавал энэ нь хоёр "багц" байх тул нарийн төвөгтэй функц болно. Диаграмыг үзнэ үү:

За, одоо яв. "Боох" функцүүдийн дарааллыг бичнэ үү:
\(y=cos((sinx))\)
\(y=5^(x^7)\)
\(y=arctg(11^x)\)
\(y=log_2(1+x)\)
Хариултууд нь нийтлэлийн төгсгөлд дахин байна.
Дотоод болон гадаад функцууд
Бид яагаад үүрлэх функцийг ойлгох хэрэгтэй байна вэ? Энэ нь бидэнд юу өгөх вэ? Баримт нь ийм дүн шинжилгээ хийхгүйгээр бид дээр дурдсан функцүүдийн деривативуудыг найдвартай олох боломжгүй юм.
Мөн цааш явахын тулд бидэнд дотоод болон гадаад функц гэсэн хоёр ойлголт хэрэгтэй болно. Энэ бол маш энгийн зүйл, үүнээс гадна бид эдгээрийг аль хэдийн задлан шинжилсэн: хэрэв бид өөрсдийн аналогийг эхэндээ санаж байвал дотоод функц нь "багц", гадаад функц нь "хайрцаг" юм. Тэдгээр. Юуны өмнө X нь "боож" байгаа нь дотоод функц бөгөөд дотоод функц нь аль хэдийн гадаад байна. Яагаад гэдэг нь ойлгомжтой - тэр гадаа байгаа, энэ нь гаднах гэсэн үг юм.
Энэ жишээнд: \(y=tg(log_2x)\), \(\log_2x\) функц нь дотоод бөгөөд  - гадна.
- гадна.
Үүнд: \(y=\cos((x^3+2x+1))\), \(x^3+2x+1\) дотоод, мөн  - гадна.
- гадна.
Нарийн төвөгтэй функцүүдэд дүн шинжилгээ хийх сүүлчийн дадлагаа дуусгаад эцэст нь бидний эхлүүлсэн зүйл рүү шилжье - бид нарийн төвөгтэй функцүүдийн деривативуудыг олох болно.
Хүснэгтийн хоосон зайг бөглөнө үү:
Нарийн төвөгтэй функцийн дериватив
Сайн байцгаана уу, бид эцэст нь энэ сэдвийн "дарга" -д хүрлээ - үнэндээ нарийн төвөгтэй функцийн дериватив, ялангуяа өгүүллийн эхнээс тэр маш аймшигтай томьёо.☺
\((f(g(x))"=f"(g(x))\cdot g"(x)\)
Энэ томъёог дараах байдлаар уншина.
Нийлмэл функцийн уламжлал нь тогтмол дотоод функц болон дотоод функцийн деривативын гадаад функцийн деривативын үржвэртэй тэнцүү байна.
Юу болохыг ойлгохын тулд "үгээр үгээр" задлан шинжлэх диаграмыг нэн даруй хараарай.

"Үүсмэл" болон "бүтээгдэхүүн" гэсэн нэр томъёо нь ямар ч хүндрэл учруулахгүй гэж найдаж байна. "Цогцолбор функц" - бид үүнийг аль хэдийн ангилсан. Барилт нь "тогтмол дотоод функцтэй холбоотой гадаад функцийн дериватив"-д байна. Энэ юу вэ?
Хариулт: Энэ бол зөвхөн гадаад функц өөрчлөгддөг, дотоод функц нь өөрчлөгддөг гадаад функцийн ердийн уламжлал юм. Одоо хүртэл тодорхойгүй байна уу? За, жишээ татъя.
\(y=\sin(x^3)\) функцтэй болгоё. Энд дотоод функц нь \(x^3\), гадаад функц болох нь тодорхой байна  . Одоо байнгын дотоод засалтай холбоотой гадна талын деривативыг олцгооё.
. Одоо байнгын дотоод засалтай холбоотой гадна талын деривативыг олцгооё.
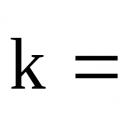 Урвалын хурдны тогтмол Лабораторийн ажлын удирдамж
Урвалын хурдны тогтмол Лабораторийн ажлын удирдамж Үхлийн дараах амьдрал бий юу?
Үхлийн дараах амьдрал бий юу? Эрдэмтэд: Дэлхий бол хүн төрөлхтний "сансрын шорон" Эрдэмтэд: Дэлхий бол сансрын шорон
Эрдэмтэд: Дэлхий бол хүн төрөлхтний "сансрын шорон" Эрдэмтэд: Дэлхий бол сансрын шорон