Шугаман тэгшитгэл гэж юу вэ. Шугаман тэгшитгэлийн системийн жишээ: шийдлийн арга
Шугаман тэгшитгэлийн систем нь тус бүр нь k хувьсагч агуулсан n шугаман тэгшитгэлийн нэгдэл юм. Үүнийг ингэж бичсэн байна.
Олон хүмүүс дээд алгебртай анх удаа таарч байхдаа тэгшитгэлийн тоо нь хувьсагчийн тоотой заавал давхцах ёстой гэж андуурдаг. Сургуулийн алгебрийн хувьд энэ нь ихэвчлэн тохиолддог боловч дээд алгебрийн хувьд энэ нь ерөнхийдөө үнэн биш юм.
Тэгшитгэлийн системийн шийдэл нь тоонуудын дараалал (k 1, k 2, ..., k n) бөгөөд энэ нь системийн тэгшитгэл бүрийн шийдэл, өөрөөр хэлбэл. Энэ тэгшитгэлд x 1, x 2, ..., x n хувьсагчдын оронд орлуулахад зөв тоон тэгшитгэлийг өгнө.
Үүний дагуу тэгшитгэлийн системийг шийдэх нь түүний бүх шийдлийн олонлогийг олох эсвэл энэ олонлог хоосон гэдгийг батлах гэсэн үг юм. Тэгшитгэлийн тоо болон үл мэдэгдэх тоо нь давхцахгүй байж болох тул гурван тохиолдол байж болно.
- Систем нь тогтворгүй, i.e. бүх шийдлийн багц хоосон байна. Системийг шийдэхийн тулд ямар арга хэрэглэж байгаагаас үл хамааран амархан илрүүлдэг нэлээд ховор тохиолдол.
- Систем нь тууштай, шийдэмгий, өөрөөр хэлбэл. яг нэг шийдэлтэй. Сургуулиас хойш сайн мэддэг сонгодог хувилбар.
- Систем нь тууштай, тодорхойгүй, i.e. хязгааргүй олон шийдэлтэй. Энэ бол хамгийн хэцүү сонголт юм. "Систем нь хязгааргүй олон шийдлүүдтэй" гэж хэлэх нь хангалтгүй бөгөөд энэ багц хэрхэн бүтэцлэгдсэнийг тайлбарлах шаардлагатай.
x i хувьсагч нь системийн зөвхөн нэг тэгшитгэлд багтсан, 1-ийн коэффициенттэй бол зөвшөөрөгдөх гэж нэрлэгддэг. Өөрөөр хэлбэл, бусад тэгшитгэлд x i хувьсагчийн коэффициент тэгтэй тэнцүү байх ёстой.
Хэрэв бид тэгшитгэл бүрт зөвшөөрөгдсөн хувьсагчийг сонговол бүхэл тэгшитгэлийн системийн зөвшөөрөгдсөн хувьсагчийн багцыг олж авна. Энэ хэлбэрээр бичигдсэн систем өөрөө шийдэгдсэн гэж нэрлэгдэх болно. Ерөнхийдөө нэг анхны системийг өөр өөр зөвшөөрөгдсөн систем болгон бууруулж болох боловч одоогоор бид үүнд санаа зовохгүй байна. Зөвшөөрөгдсөн системийн жишээ энд байна:

Хоёр систем хоёулаа x 1 , x 3 болон x 4 хувьсагчдаас хамаарч шийдэгддэг. Гэсэн хэдий ч, ижил амжилтаар хоёр дахь системийг x 1, x 3, x 5-ийн хувьд шийдсэн гэж үзэж болно. Хамгийн сүүлчийн тэгшитгэлийг x 5 = x 4 хэлбэрээр дахин бичихэд хангалттай.
Одоо илүү ерөнхий тохиолдлыг авч үзье. Нийт k хувьсагчтай байцгаая, үүнээс r нь зөвшөөрөгдөнө. Дараа нь хоёр тохиолдол боломжтой:
- Зөвшөөрөгдсөн хувьсагчийн тоо r нь нийт k хувьсагчийн тоотой тэнцүү байна: r = k. Бид r = k зөвшөөрөгдсөн хувьсагчтай k тэгшитгэлийн системийг олж авдаг. Ийм систем нь хамтарсан бөгөөд тодорхой, учир нь x 1 = b 1, x 2 = b 2, ..., x k = b k;
- Зөвшөөрөгдсөн хувьсагчийн тоо r бага байна нийт тоохувьсагч k : r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Тиймээс, дээрх системүүдэд x 2, x 5, x 6 (эхний системийн хувьд) ба x 2, x 5 (хоёр дахь системийн хувьд) хувьсагчууд үнэ төлбөргүй байдаг. Чөлөөт хувьсагч байгаа тохиолдолд теорем хэлбэрээр илүү сайн томъёолсон болно.
Анхаарна уу: энэ маш их чухал цэг! Үүссэн системийг хэрхэн бичихээс хамааран ижил хувьсагч нь зөвшөөрөгдсөн эсвэл үнэгүй байж болно. Ихэнх дээд математикийн багш нар хувьсагчдыг толь бичгийн дарааллаар бичихийг зөвлөж байна, жишээлбэл. өсөх индекс. Гэсэн хэдий ч та энэ зөвлөмжийг дагаж мөрдөх үүрэг хүлээхгүй.
Теорем. Хэрэв n тэгшитгэлийн системд x 1, x 2, ..., x r хувьсагчдыг зөвшөөрч, x r + 1, x r + 2, ..., x k хувьсагчдыг чөлөөтэй гэж үзвэл:
- Хэрэв бид чөлөөт хувьсагчдын утгуудыг (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k) тогтоож, x 1, x 2 утгуудыг олбол, ..., x r, бид шийдвэрүүдийн аль нэгийг авдаг.
- Хэрэв хоёр шийдэлд чөлөөт хувьсагчдын утгууд давхцаж байвал зөвшөөрөгдсөн хувьсагчдын утгууд давхцдаг, өөрөөр хэлбэл. шийдэл нь тэнцүү байна.
Энэ теоремын утга учир юу вэ? Шийдвэрлэсэн тэгшитгэлийн системийн бүх шийдлийг олж авахын тулд чөлөөт хувьсагчдыг тусгаарлахад хангалттай. Дараа нь чөлөөт хувьсагчдад өөр утгыг оноож өгснөөр бид олж авна бэлэн шийдлүүд. Энэ бол бүх зүйл - ийм байдлаар та системийн бүх шийдлүүдийг авах боломжтой. Өөр шийдэл байхгүй.
Дүгнэлт: Шийдвэрлэсэн тэгшитгэлийн систем нь үргэлж нийцтэй байдаг. Шийдвэрлэсэн систем дэх тэгшитгэлийн тоо хувьсагчийн тоотой тэнцүү бол систем тодорхой, бага бол тодорхойгүй байна.
Бүх зүйл сайхан байх болно, гэхдээ асуулт гарч ирнэ: анхны тэгшитгэлийн системээс шийдэгдсэнийг хэрхэн олж авах вэ? Үүний тулд бий
Бусад төрлийн тэгшитгэлүүдтэй танилцах нь логик юм. Дараагийн эгнээнд байна шугаман тэгшитгэл, зорилтот судалгаа нь 7-р ангийн алгебрийн хичээлээс эхэлдэг.
Эхлээд шугаман тэгшитгэл гэж юу болохыг тайлбарлаж, шугаман тэгшитгэлийн тодорхойлолт, түүний коэффициентийг өгч, харуулах хэрэгтэй. ерөнхий хэлбэр. Дараа нь коэффициентүүдийн утга, үндсийг хэрхэн олох зэргээс хамаарч шугаман тэгшитгэлийн хэдэн шийдэл байгааг олж мэдэх боломжтой. Энэ нь жишээнүүдийг шийдвэрлэхэд шилжих, улмаар сурсан онолоо нэгтгэх боломжийг олгоно. Энэ нийтлэлд бид үүнийг хийх болно: шугаман тэгшитгэл, тэдгээрийн шийдлүүдтэй холбоотой бүх онолын болон практик цэгүүдийг нарийвчлан авч үзэх болно.
Энд бид зөвхөн нэг хувьсагчтай шугаман тэгшитгэлийг авч үзэх болно гэж шууд хэлье, мөн тусдаа өгүүллээр бид шийдлийн зарчмуудыг судлах болно. хоёр хувьсагчтай шугаман тэгшитгэл.
Хуудасны навигаци.
Шугаман тэгшитгэл гэж юу вэ?
Шугаман тэгшитгэлийн тодорхойлолтыг бичсэн байдлаар нь өгдөг. Түүгээр ч зогсохгүй математик, алгебрийн өөр өөр сурах бичигт шугаман тэгшитгэлийн тодорхойлолтын томъёолол нь асуудлын мөн чанарт нөлөөлдөггүй зарим ялгаатай байдаг.
Жишээлбэл, Ю.Н.Макарычев нарын 7-р ангийн алгебрийн сурах бичигт шугаман тэгшитгэлийг дараах байдлаар тодорхойлсон.
Тодорхойлолт.
Маягтын тэгшитгэл a x=b, энд x нь хувьсагч, a ба b нь зарим тоонуудыг нэрлэдэг нэг хувьсагчтай шугаман тэгшитгэл.
Тодорхойлолтыг хангасан шугаман тэгшитгэлийн жишээг өгье. Жишээлбэл, 5 x = 10 нь нэг x хувьсагчтай шугаман тэгшитгэл бөгөөд энд a коэффициент 5, b тоо нь 10 байна. Өөр нэг жишээ: −2.3·y=0 нь мөн шугаман тэгшитгэл боловч y хувьсагчтай, a=−2.3 ба b=0. Шугаман тэгшитгэлд x=−2 ба −x=3.33 a нь тодорхой байхгүй бөгөөд 1 ба −1-тэй тэнцүү байх ба эхний тэгшитгэлд b=−2, хоёр дахь тэгшитгэлд b=3.33 байна.
Жилийн өмнө Н.Я.Виленкиний математикийн сурах бичигт нэг үл мэдэгдэх шугаман тэгшитгэлийг a x = b хэлбэрийн тэгшитгэлээс гадна нэг хэсгээс нэр томъёог шилжүүлэх замаар энэ хэлбэрт оруулж болох тэгшитгэлийг авч үзсэн болно. тэгшитгэлийг эсрэг тэмдэгтэй нөгөө рүү, түүнчлэн ижил төстэй нэр томъёог багасгах замаар. Энэ тодорхойлолтын дагуу 5 x = 2 x + 6 хэлбэрийн тэгшитгэлүүд гэх мэт. мөн шугаман.
Хариуд нь A. G. Mordkovich-ийн 7-р ангийн алгебрийн сурах бичигт дараахь тодорхойлолтыг өгсөн болно.
Тодорхойлолт.
Нэг x хувьсагчтай шугаман тэгшитгэл a·x+b=0 хэлбэрийн тэгшитгэл бөгөөд a ба b нь шугаман тэгшитгэлийн коэффициент гэж нэрлэгддэг зарим тоонууд юм.
Жишээлбэл, ийм төрлийн шугаман тэгшитгэлүүд нь 2 x−12=0, энд a коэффициент нь 2, b нь −12-тэй тэнцүү, a=0,2 ба b =4,6 коэффициенттэй 0,2 y+4,6=0 байна. Гэхдээ үүнтэй зэрэгцэн a·x+b=0 биш, харин a·x=b хэлбэртэй, жишээлбэл, 3·x=12 хэлбэртэй шугаман тэгшитгэлийн жишээнүүд байдаг.
Ирээдүйд ямар ч зөрүү гарахгүйн тулд нэг x хувьсагчтай, a ба b коэффициенттэй шугаман тэгшитгэлээр a x + b = 0 хэлбэрийн тэгшитгэлийг хэлье. Шугаман тэгшитгэл нь тийм учраас энэ төрлийн шугаман тэгшитгэл нь хамгийн үндэслэлтэй юм шиг санагддаг алгебрийн тэгшитгэлнэгдүгээр зэрэг. Дээр дурдсан бусад бүх тэгшитгэлүүд, түүнчлэн эквивалент хувиргалтыг ашиглан a x + b = 0 хэлбэрт буулгасан тэгшитгэлүүдийг бид дуудах болно. шугаман тэгшитгэл болгон бууруулсан тэгшитгэлүүд. Энэ хандлагаар 2 x+6=0 тэгшитгэл нь шугаман тэгшитгэл бөгөөд 2 x=−6, 4+25 y=6+24 y, 4 (x+5)=12 гэх мэт. - Эдгээр нь шугаман болж буурдаг тэгшитгэлүүд юм.
Шугаман тэгшитгэлийг хэрхэн шийдэх вэ?
Одоо a·x+b=0 шугаман тэгшитгэлүүд хэрхэн шийдэгдэж байгааг олж мэдэх цаг болжээ. Өөрөөр хэлбэл, шугаман тэгшитгэл үндэстэй эсэх, хэрэв үндэстэй бол хэд нь, яаж олох вэ гэдгийг мэдэх цаг болжээ.
Шугаман тэгшитгэлийн үндэс байгаа эсэх нь a ба b коэффициентүүдийн утгаас хамаарна. Энэ тохиолдолд a x+b=0 шугаман тэгшитгэлтэй байна
- a≠0-ийн цорын ганц үндэс,
- a=0 ба b≠0-ийн үндэс байхгүй,
- a=0 ба b=0-ийн хувьд хязгааргүй олон үндэстэй бөгөөд энэ тохиолдолд дурын тоо нь шугаман тэгшитгэлийн үндэс болно.
Эдгээр үр дүнг хэрхэн олж авсныг тайлбарлая.
Тэгшитгэлийг шийдэхийн тулд бид анхны тэгшитгэлээс эквивалент тэгшитгэл рүү, өөрөөр хэлбэл ижил язгууртай эсвэл анхных шиг үндэсгүй тэгшитгэл рүү шилжиж болно гэдгийг бид мэднэ. Үүнийг хийхийн тулд та дараахь ижил төстэй хувиргалтыг ашиглаж болно.
- тэгшитгэлийн нэг талаас нөгөө тал руу эсрэг тэмдэгтэй нэр томъёог шилжүүлэх;
- түүнчлэн тэгшитгэлийн хоёр талыг ижил тэг биш тоогоор үржүүлэх буюу хуваах.
Тэгэхээр a·x+b=0 хэлбэрийн нэг хувьсагчтай шугаман тэгшитгэлд b гишүүнийг зүүн талаас баруун тал руу нь эсрэг тэмдгээр шилжүүлж болно. Энэ тохиолдолд тэгшитгэл нь a·x=−b хэлбэртэй болно.
Дараа нь тэгшитгэлийн хоёр талыг а тоонд хуваах асуулт гарч ирнэ. Гэхдээ нэг зүйл бий: a тоо тэгтэй тэнцүү байж болох бөгөөд энэ тохиолдолд ийм хуваагдах боломжгүй юм. Энэ асуудлыг шийдэхийн тулд эхлээд а тоог тэг биш гэж үзэх ба тэгтэй тэнцүү байх тохиолдлыг хэсэг хугацааны дараа тусад нь авч үзэх болно.
Тэгэхээр, a нь тэгтэй тэнцүү биш үед a·x=−b тэгшитгэлийн хоёр талыг a-д хувааж, дараа нь x=(−b):a хэлбэрт шилжинэ. зэрэг бутархай зураасыг ашиглан бичнэ.
Иймд a≠0-ийн хувьд шугаман тэгшитгэл нь a·x+b=0 нь тэгшитгэлтэй тэнцэх бөгөөд үүнээс үндэс нь харагдаж байна.
Энэ үндэс нь өвөрмөц, өөрөөр хэлбэл шугаман тэгшитгэл нь өөр үндэсгүй гэдгийг харуулахад хялбар байдаг. Энэ нь эсрэг аргыг хийх боломжийг танд олгоно.
Үндэсийг x 1 гэж тэмдэглэе. Шугаман тэгшитгэлийн өөр язгуур байгаа гэж үзье, бид үүнийг x 2 гэж тэмдэглэж, x 2 ≠x 1 гэж тэмдэглэе. ялгаагаар тэнцүү тоог тодорхойлохнь x 1 −x 2 ≠0 нөхцөлтэй тэнцүү байна. x 1 ба x 2 нь a·x+b=0 шугаман тэгшитгэлийн үндэс учир a·x 1 +b=0, a·x 2 +b=0 тоон тэгшитгэлүүд биелнэ. Тоон тэгшитгэлийн шинж чанарууд нь үүнийг хийх боломжийг олгодог эдгээр тэгшитгэлүүдийн харгалзах хэсгүүдийг хасаж болно, бид a·x 1 +b−(a·x 2 +b)=0−0, үүнээс a·(x 1) байна. −x 2)+( b−b)=0, дараа нь a·(x 1 −x 2)=0 . Гэхдээ a≠0 ба x 1 − x 2 ≠0 хоёулаа байх тул энэ тэгш байдал боломжгүй юм. Ингээд бид a≠0-ийн хувьд a·x+b=0 шугаман тэгшитгэлийн язгуур өвөрмөц болохыг баталж буй зөрчилдөөнд хүрлээ.
Ингээд a≠0-ийн хувьд a·x+b=0 шугаман тэгшитгэлийг шийдсэн. Энэ зүйлийн эхэнд өгсөн эхний үр дүн үндэслэлтэй байна. a=0 нөхцөлийг хангасан хоёр өөр үлдлээ.
a=0 үед a·x+b=0 шугаман тэгшитгэл 0·x+b=0 хэлбэрийг авна. Энэ тэгшитгэл ба тоог тэгээр үржүүлэх шинж чанараас үзэхэд ямар ч тоог х гэж авсан бай 0 x + b=0 тэгшитгэлд орлуулахад b=0 тоон тэгшитгэл үүснэ. Энэ тэгш байдал b=0 үед үнэн, бусад тохиолдолд b≠0 үед энэ тэгшитгэл худал байна.
Иймээс a=0 ба b=0 байхад дурын тоо нь a·x+b=0 шугаман тэгшитгэлийн үндэс болно, учир нь эдгээр нөхцөлд x-ийн оронд дурын тоог орлуулснаар 0=0 зөв тоон тэгшитгэл гарч ирнэ. Мөн a=0 ба b≠0 үед a·x+b=0 шугаман тэгшитгэл нь үндэсгүй, учир нь эдгээр нөхцөлд x-ийн оронд дурын тоог орлуулах нь буруу тоон тэгшитгэл b=0 гарахад хүргэдэг.
Өгөгдсөн үндэслэлүүд нь ямар ч шугаман тэгшитгэлийг шийдвэрлэх боломжийг олгодог үйлдлийн дарааллыг боловсруулах боломжийг бидэнд олгодог. Тэгэхээр, шугаман тэгшитгэлийг шийдвэрлэх алгоритмнь:
- Нэгдүгээрт, шугаман тэгшитгэлийг бичснээр бид a ба b коэффициентүүдийн утгыг олно.
- Хэрэв a=0 ба b=0 бол энэ тэгшитгэл нь хязгааргүй олон үндэстэй, тухайлбал дурын тоо нь энэ шугаман тэгшитгэлийн үндэс болно.
- Хэрэв a тэгээс ялгаатай бол
- b коэффициентийг эсрэг тэмдгээр баруун тийш шилжүүлж, шугаман тэгшитгэлийг a·x=−b хэлбэрт шилжүүлнэ.
- Үүний дараа үүссэн тэгшитгэлийн хоёр талыг тэгээс өөр a тоонд хувааснаар анхны шугаман тэгшитгэлийн хүссэн язгуурыг өгнө.
Бичсэн алгоритм нь шугаман тэгшитгэлийг хэрхэн шийдвэрлэх вэ гэсэн асуултын цогц хариулт юм.
Энэ зүйлийг дүгнэж хэлэхэд үүнтэй төстэй алгоритмыг a·x=b хэлбэрийн тэгшитгэлийг шийдвэрлэхэд ашигладаг гэдгийг хэлэх нь зүйтэй болов уу. Үүний ялгаа нь a≠0 үед тэгшитгэлийн хоёр тал нэн даруй энэ тоонд хуваагддаг; энд b нь тэгшитгэлийн шаардлагатай хэсэгт аль хэдийн орсон бөгөөд үүнийг шилжүүлэх шаардлагагүй болно.
a x = b хэлбэрийн тэгшитгэлийг шийдвэрлэхийн тулд дараах алгоритмыг ашиглана.
- Хэрэв a=0 ба b=0 бол тэгшитгэл нь дурын тоо болох хязгааргүй олон үндэстэй байна.
- Хэрэв a=0 ба b≠0 бол анхны тэгшитгэл нь үндэсгүй болно.
- Хэрэв a нь тэг биш бол тэгшитгэлийн хоёр тал нь тэг биш a тоонд хуваагдах бөгөөд үүнээс тэгшитгэлийн цорын ганц язгуур олдох нь b/a-тай тэнцүү байна.
Шугаман тэгшитгэлийг шийдвэрлэх жишээ
Дасгал руугаа явцгаая. Шугаман тэгшитгэлийг шийдвэрлэх алгоритмыг хэрхэн ашиглаж байгааг харцгаая. Шугаман тэгшитгэлийн коэффициентүүдийн өөр өөр утгатай тохирох ердийн жишээнүүдийн шийдлийг танилцуулъя.
Жишээ.
0·x−0=0 шугаман тэгшитгэлийг шийд.
Шийдэл.
Энэ шугаман тэгшитгэлд a=0 ба b=−0 байгаа нь b=0-тэй ижил байна. Иймд энэ тэгшитгэл нь хязгааргүй олон үндэстэй бөгөөд дурын тоо нь энэ тэгшитгэлийн үндэс юм.
Хариулт:
x - дурын тоо.
Жишээ.
0 x + 2.7 = 0 шугаман тэгшитгэл нь шийдтэй юу?
Шийдэл.
Энэ тохиолдолд а коэффициент нь тэгтэй тэнцүү бөгөөд энэ шугаман тэгшитгэлийн b коэффициент нь 2.7-тэй тэнцүү, өөрөөр хэлбэл тэгээс ялгаатай байна. Тиймээс шугаман тэгшитгэл нь үндэсгүй.
Тэгшитгэл. Өөрөөр хэлбэл, бүх тэгшитгэлийн шийдэл нь эдгээр өөрчлөлтүүдээс эхэлдэг. Шугаман тэгшитгэлийг шийдвэрлэхдээ энэ нь (шийдвэр) нь таних тэмдгийн хувиргалт дээр суурилдаг бөгөөд эцсийн хариултаар төгсдөг.
Үл мэдэгдэх хувьсагчийн хувьд тэгээс ялгаатай коэффициентийн тохиолдол.
ax+b=0, a ≠ 0
Бид X-тэй нэр томъёог нэг тал руу, тоонуудыг нөгөө тал руу шилжүүлдэг. Нөхцөлүүдийг тэгшитгэлийн эсрэг тал руу шилжүүлэхдээ тэмдгийг өөрчлөх хэрэгтэй гэдгийг санаарай.
сүх:(а)=-б:(а)
Богино болгоё Ацагт Xмөн бид авах:
x=-b:(a)
Энэ бол хариулт юм. Хэрэв та дугаар байгаа эсэхийг шалгах шаардлагатай бол -б:(а)тэгшитгэлийнхээ язгуурын оронд бид анхны тэгшитгэлд орлуулах хэрэгтэй Xэнэ тоо:
a(-b:(a))+b=0 (тэдгээр. 0=0)
Учир нь тэгвэл энэ тэгш байдал зөв -б:(а)үнэн бол тэгшитгэлийн үндэс юм.
Хариулт: x=-b:(a), a ≠ 0.
Эхний жишээ:
5х+2=7х-6
Бид гишүүдийг нэг тал руу шилжүүлдэг X, нөгөө талд нь тоонууд:
5х-7х=-6-2
-2х:(-2)=-8:(-2)
Үл мэдэгдэх хүчин зүйлийн хувьд бид коэффициентийг бууруулж дараах хариултыг авсан.
Энэ бол хариулт юм. Хэрэв та 4 тоо нь бидний тэгшитгэлийн үндэс мөн эсэхийг шалгах шаардлагатай бол бид анхны тэгшитгэлийн X-ийн оронд энэ тоог орлуулна.
5*4+2=7*4-6 (тэдгээр. 22=22)
Учир нь Энэ тэгшитгэл үнэн бол 4 нь тэгшитгэлийн үндэс болно.
Хоёр дахь жишээ:
Тэгшитгэлийг шийд:
5х+14=х-49
Үл мэдэгдэх болон тоонуудыг өөр өөр чиглэлд шилжүүлснээр бид дараахь зүйлийг олж авлаа.
Тэгшитгэлийн хэсгүүдийг at коэффициентээр хуваана x(4-ээр) ба бид дараахь зүйлийг авна.
![]()
Гурав дахь жишээ:
Тэгшитгэлийг шийд:
![]()
Нэгдүгээрт, бид бүх гишүүнийг дараах байдлаар үржүүлснээр үл мэдэгдэх коэффициентийн зохисгүй байдлаас ангижрах болно.
![]()
![]()
Энэ хэлбэрийг хялбаршуулсан гэж үздэг, учир нь тоо нь хуваагч дахь тооны язгууртай байна. Тоолуур ба хуваагчийг ижил тоогоор үржүүлэх замаар хариултыг хялбарчлах шаардлагатай бол бидэнд дараах зүйл байна.
![]()
Шийдэл байхгүй тохиолдол.
Тэгшитгэлийг шийд:
2х+3=2х+7
Хүн бүрийн өмнө xбидний тэгшитгэл жинхэнэ тэгшитгэл болохгүй. Энэ нь бидний тэгшитгэлд үндэс байхгүй гэсэн үг юм.
Хариулт: шийдэл байхгүй.
Онцгой тохиолдол бол хязгааргүй тооны шийдэл юм.
Тэгшитгэлийг шийд:
2х+3=2х+3
X ба тоог өөр чиглэлд шилжүүлж, ижил төстэй нэр томъёог нэмснээр бид тэгшитгэлийг олж авна.
Энд ч гэсэн хоёр хэсгийг 0-д хуваах боломжгүй, учир нь энэ нь хориотой. Гэсэн хэдий ч, байрлуулах Xямар ч тоо, бид зөв тэгш байдлыг олж авдаг. Өөрөөр хэлбэл, тоо бүр ийм тэгшитгэлийн шийдэл юм. Тиймээс хязгааргүй олон тооны шийдэл байдаг.
Хариулт: хязгааргүй тооны шийдлүүд.
Хоёр бүрэн хэлбэрийн тэгш байдлын тохиолдол.
ax+b=cx+d
ax-cx=d-b
(a-c)x=d-b
x=(d-b):(a-c)
Хариулт: x=(d-b):(a-c), Хэрэв d≠b ба a≠c, эс бөгөөс хязгааргүй олон шийдэл байдаг, гэхдээ хэрэв a=c, А d≠b, тэгвэл ямар ч шийдэл байхгүй.
Энэ видеон дээр бид ижил алгоритмыг ашиглан шийдсэн шугаман тэгшитгэлийн бүхэл бүтэн багцыг шинжлэх болно - тиймээс тэдгээрийг хамгийн энгийн гэж нэрлэдэг.
Эхлээд тодорхойлъё: шугаман тэгшитгэл гэж юу вэ, аль нь хамгийн энгийн гэж нэрлэгддэг вэ?
Шугаман тэгшитгэл гэдэг нь зөвхөн нэг хувьсагчтай, зөвхөн нэгдүгээр зэрэгтэй тэгшитгэл юм.
Хамгийн энгийн тэгшитгэл нь бүтээцийг хэлнэ:
Бусад бүх шугаман тэгшитгэлийг алгоритмыг ашиглан хамгийн энгийн болгон бууруулна.
- Хэрэв байгаа бол хашилтыг дэлгэнэ үү;
- Хувьсагч агуулсан нэр томъёог тэнцүү тэмдгийн нэг тал руу, хувьсагчгүй нөхцөлийг нөгөө тал руу нь шилжүүлэх;
- Тэнцүү тэмдгийн зүүн ба баруун талд ижил төстэй нэр томъёог өгөх;
- Гарсан тэгшитгэлийг $x$ хувьсагчийн коэффициентэд хуваа.
Мэдээжийн хэрэг, энэ алгоритм нь үргэлж тусалдаггүй. Баримт нь заримдаа эдгээр бүх заль мэх хийсний дараа $ x $ хувьсагчийн коэффициент тэгтэй тэнцүү болж хувирдаг. Энэ тохиолдолд хоёр сонголт байж болно:
- Тэгшитгэлд шийдэл огт байхгүй. Жишээлбэл, $0\cdot x=8$ гэх мэт зүйл гарч ирэхэд, i.e. зүүн талд нь тэг, баруун талд нь тэгээс өөр тоо байна. Доорх видеон дээр бид ийм нөхцөл байдал үүсч болох хэд хэдэн шалтгааныг авч үзэх болно.
- Шийдэл нь бүх тоо юм. Тэгшитгэлийг $0\cdot x=0$ бүтэц болгон бууруулсан тохиолдолд ийм боломжтой болох цорын ганц тохиолдол юм. Бид ямар ч $x$-г орлуулахаас үл хамааран "тэг нь тэгтэй тэнцүү" болж хувирах нь маш логик юм. зөв тоон тэгшитгэл.
Одоо энэ бүхэн хэрхэн явагддагийг бодит жишээн дээр харцгаая.
Тэгшитгэлийг шийдвэрлэх жишээ
Өнөөдөр бид шугаман тэгшитгэлүүдтэй харьцаж байгаа бөгөөд зөвхөн хамгийн энгийн тэгшитгэлүүд юм. Ерөнхийдөө шугаман тэгшитгэл гэдэг нь яг нэг хувьсагчийг агуулсан аливаа тэгшитгэлийг хэлдэг бөгөөд энэ нь зөвхөн эхний зэрэгтэй байдаг.
Ийм бүтээн байгуулалтыг ойролцоогоор ижил аргаар шийддэг.
- Юуны өмнө, хэрэв байгаа бол (бидний сүүлийн жишээн дээрх шиг) хаалтуудыг өргөжүүлэх хэрэгтэй;
- Дараа нь ижил төстэй зүйлийг нэгтгэнэ
- Эцэст нь хувьсагчийг тусгаарлах, i.e. хувьсагчтай холбоотой бүх зүйлийг буюу түүнд агуулагдаж буй нэр томьёог нэг тал руу шилжүүлж, үүнгүйгээр үлдсэн бүх зүйлийг нөгөө тал руу шилжүүлнэ.
Дараа нь дүрмээр бол та үүссэн тэгш байдлын тал бүр дээр ижил төстэй зүйлийг өгөх хэрэгтэй бөгөөд үүний дараа "x" коэффициентээр хуваах л үлддэг бөгөөд бид эцсийн хариултыг авах болно.
Онолын хувьд энэ нь сайхан бөгөөд энгийн мэт харагддаг боловч практик дээр ахлах сургуулийн туршлагатай сурагчид хүртэл маш энгийн шугаман тэгшитгэл дээр доромжилсон алдаа гаргаж чаддаг. Ихэвчлэн хаалт нээх эсвэл "нэмэх", "хасах" -ыг тооцоолоход алдаа гардаг.
Нэмж дурдахад, шугаман тэгшитгэл нь огт шийдэлгүй, эсвэл шийдэл нь бүхэл тооны шугам байх тохиолдол гардаг. ямар ч тоо. Өнөөдрийн хичээл дээр бид эдгээр нарийн ширийн зүйлийг авч үзэх болно. Гэхдээ та аль хэдийн ойлгосноор бид хамгийн энгийн ажлуудаас эхлэх болно.
Энгийн шугаман тэгшитгэлийг шийдвэрлэх схем
Эхлээд хамгийн энгийн шугаман тэгшитгэлийг шийдэх бүх схемийг дахин бичье.
- Хэрэв байгаа бол хаалтуудыг өргөжүүлнэ үү.
- Бид хувьсагчдыг тусгаарладаг, өөрөөр хэлбэл. Бид "X"-ийг агуулсан бүх зүйлийг нэг тал руу, "X"-гүй бүгдийг нөгөө тал руу шилжүүлдэг.
- Бид ижил төстэй нэр томъёог танилцуулж байна.
- Бид бүгдийг "x" коэффициентээр хуваадаг.
Мэдээжийн хэрэг, энэ схем үргэлж ажилладаггүй, үүнд тодорхой нарийн мэдрэмж, заль мэх байдаг бөгөөд одоо бид тэдэнтэй танилцах болно.
Энгийн шугаман тэгшитгэлийн бодит жишээг шийдвэрлэх
Даалгавар №1
Эхний алхам нь бид хаалт нээхийг шаарддаг. Гэхдээ тэд энэ жишээнд байхгүй тул бид тэдгээрийг алгасдаг энэ үе шат. Хоёр дахь шатанд бид хувьсагчдыг тусгаарлах хэрэгтэй. Анхаарна уу: бид зөвхөн хувь хүний нэр томъёоны тухай ярьж байна. Үүнийг бичье:
Бид зүүн болон баруун талд ижил төстэй нэр томъёог танилцуулж байна, гэхдээ үүнийг энд аль хэдийн хийсэн. Тиймээс бид дөрөв дэх алхам руу шилжиж байна: коэффициентээр хуваана:
\[\frac(6x)(6)=-\frac(72)(6)\]
Тиймээс бид хариултаа авлаа.
Даалгавар №2
Бид энэ асуудлын хаалтуудыг харж байгаа тул тэдгээрийг өргөжүүлье:
Зүүн ба баруун талд хоёулаа бид ойролцоогоор ижил загварыг харж байна, гэхдээ алгоритмын дагуу ажиллацгаая, өөрөөр хэлбэл. хувьсагчдыг ялгах:
Энд зарим ижил төстэй зүйлс байна:
Энэ нь ямар үндэс дээр ажилладаг вэ? Хариулт: аль ч тохиолдолд. Тиймээс бид $x$ нь дурын тоо гэж бичиж болно.
Даалгавар №3
Гурав дахь шугаман тэгшитгэл нь илүү сонирхолтой юм:
\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]
Хэд хэдэн хаалт байгаа боловч тэдгээрийг юугаар ч үржүүлдэггүй, зүгээр л өмнө нь бичдэг янз бүрийн шинж тэмдэг. Тэдгээрийг задалж үзье:
Бид аль хэдийн мэдэгдэж байсан хоёр дахь алхамыг гүйцэтгэдэг:
\[-x+x+2x=15-6-12+3\]
Тооцоогоо хийцгээе:
Бид сүүлчийн алхамыг хийдэг - бүгдийг "x" коэффициентээр хуваана.
\[\frac(2x)(x)=\frac(0)(2)\]
Шугаман тэгшитгэлийг шийдвэрлэхэд анхаарах зүйлс
Хэрэв бид хэтэрхий энгийн ажлуудыг үл тоомсорловол би дараахь зүйлийг хэлмээр байна.
- Дээр хэлсэнчлэн шугаман тэгшитгэл бүр шийдэлтэй байдаггүй - заримдаа үндэс байдаггүй;
- Хэдийгээр үндэс байгаа ч гэсэн тэдний дунд тэг байж болно - үүнд буруу зүйл байхгүй.
Тэг гэдэг нь бусадтай ижил тоо тул та үүнийг ямар нэгэн байдлаар ялгаварлан гадуурхах ёсгүй, тэгвэл та буруу зүйл хийсэн гэж бодож болохгүй.
Өөр нэг онцлог нь хаалт нээхтэй холбоотой юм. Анхаарна уу: тэдний өмнө "хасах" тэмдэг байгаа бол бид үүнийг арилгадаг боловч хаалтанд тэмдэглэгээг өөрчилдөг. эсрэг. Дараа нь бид үүнийг стандарт алгоритмуудыг ашиглан нээж болно: бид дээрх тооцоололд үзсэн зүйлээ авах болно.
Энэ энгийн баримтыг ойлгох нь ахлах сургуульд байхдаа ийм зүйл хийх нь энгийн зүйл мэт санагдвал тэнэг, хор хөнөөлтэй алдаа гаргахаас зайлсхийхэд тусална.
Нарийн төвөгтэй шугаман тэгшитгэлийг шийдвэрлэх
Илүү төвөгтэй тэгшитгэл рүү шилжье. Одоо бүтэц нь илүү төвөгтэй болж, янз бүрийн хувиргалт хийх үед квадрат функц гарч ирнэ. Гэсэн хэдий ч бид үүнээс айх ёсгүй, учир нь хэрэв зохиогчийн төлөвлөгөөний дагуу шугаман тэгшитгэлийг шийдэж байгаа бол хувиргах явцад квадрат функц агуулсан бүх мономиалууд цуцлагдах болно.
Жишээ №1
Мэдээжийн хэрэг, эхний алхам бол хаалтыг нээх явдал юм. Үүнийг маш болгоомжтой хийцгээе:
Одоо нууцлалыг харцгаая:
\[-x+6((x)^(2))-6((x)^(2))+x=-12\]
Энд зарим ижил төстэй зүйлс байна:
Мэдээжийн хэрэг, энэ тэгшитгэлд шийдэл байхгүй тул бид үүнийг хариултанд бичнэ:
\[\varnothing\]
эсвэл үндэс байхгүй.
Жишээ №2
Бид ижил үйлдлийг гүйцэтгэдэг. Эхний алхам:
Хувьсагчтай бүх зүйлийг зүүн тийш, үүнгүйгээр баруун тийш шилжүүлье:
Энд зарим ижил төстэй зүйлс байна:
Мэдээжийн хэрэг, энэ шугаман тэгшитгэлд шийдэл байхгүй тул бид үүнийг дараах байдлаар бичнэ.
\[\varnothing\],
эсвэл үндэс байхгүй.
Шийдлийн нюансууд
Хоёр тэгшитгэл хоёулаа бүрэн шийдэгдсэн. Эдгээр хоёр илэрхийлэлийг жишээ болгон ашигласнаар бид хамгийн энгийн шугаман тэгшитгэлд ч гэсэн бүх зүйл тийм ч энгийн биш байж болох юм: нэг эсвэл аль нь ч биш, эсвэл хязгааргүй олон үндэс байж болно гэдгийг бид дахин батлав. Манай тохиолдолд бид хоёр тэгшитгэлийг авч үзсэн бөгөөд хоёулаа үндэсгүй.
Гэхдээ би та бүхний анхаарлыг өөр нэг баримтад хандуулахыг хүсч байна: хаалттай хэрхэн ажиллах, өмнө нь хасах тэмдэг байвал тэдгээрийг хэрхэн нээх вэ. Энэ илэрхийлэлийг анхаарч үзээрэй:
Нээхээсээ өмнө бүх зүйлийг "X" -ээр үржүүлэх хэрэгтэй. Анхаарна уу: үрждэг бие даасан нэр томъёо бүр. Дотор нь хоёр нэр томъёо байдаг - тус тус хоёр нэр томъёо ба үржүүлсэн.
Эдгээр энгийн мэт боловч маш чухал, аюултай өөрчлөлтүүд дууссаны дараа л хаалтанд хасах тэмдэг байгаа гэсэн үүднээс нээж болно. Тийм ээ, тийм: зөвхөн одоо, өөрчлөлтүүд дуусмагц бид хаалтны өмнө хасах тэмдэг байгааг санаж байгаа бөгөөд энэ нь доорх бүх зүйл тэмдгүүдийг өөрчилдөг гэсэн үг юм. Үүний зэрэгцээ хаалт нь өөрөө алга болж, хамгийн чухал нь урд талын "хасах" нь алга болно.
Бид хоёр дахь тэгшитгэлтэй ижил зүйлийг хийнэ:
Би эдгээр өчүүхэн, өчүүхэн мэт санагдах баримтуудад анхаарал хандуулж байгаа нь санамсаргүй хэрэг биш юм. Тэгшитгэлийг шийдвэрлэх нь үргэлж энгийн хувиргалтуудын дараалал байдаг тул энгийн үйлдлүүдийг тодорхой, чадварлаг хийж чадахгүй байгаа нь ахлах сургуулийн сурагчид над дээр ирж, ийм энгийн тэгшитгэлийг шийдэж сурахад хүргэдэг.
Мэдээжийн хэрэг, та эдгээр ур чадвараа автоматаар эзэмшүүлэх өдөр ирэх болно. Та дахин маш олон хувиргалт хийх шаардлагагүй болно, та бүгдийг нэг мөрөнд бичих болно. Гэхдээ та дөнгөж сурч байхдаа үйлдэл бүрийг тусад нь бичих хэрэгтэй.
Бүр илүү төвөгтэй шугаман тэгшитгэлийг шийдвэрлэх
Одоо бидний шийдэх гэж байгаа зүйлийг хамгийн энгийн ажил гэж нэрлэх аргагүй ч утга нь хэвээрээ л байна.
Даалгавар №1
\[\зүүн(7х+1 \баруун)\зүүн(3х-1 \баруун)-21((x)^(2))=3\]
Эхний хэсгийн бүх элементүүдийг үржүүлье.
Зарим нууцлалыг хийцгээе:
Энд зарим ижил төстэй зүйлс байна:
Сүүлийн алхамыг дуусгая:
\[\frac(-4x)(4)=\frac(4)(-4)\]
Энд бидний эцсийн хариулт байна. Шийдвэрлэх явцад бид квадрат функцтэй коэффициентүүдтэй байсан ч тэдгээр нь бие биенээ цуцалсан нь тэгшитгэлийг квадрат биш шугаман болгодог.
Даалгавар №2
\[\зүүн(1-4х \баруун)\зүүн(1-3х \баруун)=6х\зүүн(2х-1 \баруун)\]
Эхний алхамыг анхааралтай хийцгээе: эхний хаалтанд байгаа элемент бүрийг хоёр дахь элемент бүрээр үржүүлнэ. Өөрчлөлтийн дараа нийт дөрвөн шинэ нэр томъёо байх ёстой:
Одоо үржүүлэлтийг гишүүн бүрт анхааралтай хийцгээе:
"X"-тэй нэр томъёог зүүн тийш, байхгүй бол баруун тийш шилжүүлье.
\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]
Энд ижил төстэй нэр томъёо байна:
Дахин нэг удаа бид эцсийн хариултыг хүлээн авлаа.
Шийдлийн нюансууд
Эдгээр хоёр тэгшитгэлийн талаархи хамгийн чухал тэмдэглэл бол дараахь зүйл юм: бид нэгээс олон гишүүнтэй хаалтуудыг үржүүлж эхэлмэгц энэ нь дараах дүрмийн дагуу хийгддэг: эхний гишүүнийг эхнийхээс авч, элемент бүрээр үржүүлнэ. Хоёрдугаарт; Дараа нь бид эхнийхээс хоёр дахь элементийг авч, хоёр дахь элемент бүрээр ижил төстэй байдлаар үржүүлнэ. Үүний үр дүнд бид дөрвөн хугацаатай болно.
Алгебрийн нийлбэрийн тухай
Энэ сүүлчийн жишээгээр би оюутнуудад алгебрийн нийлбэр гэж юу болохыг сануулмаар байна. Сонгодог математикийн хувьд 1-7 доллар гэдэг нь энгийн бүтээн байгуулалтыг хэлдэг: нэгээс долоог хас. Алгебрийн хувьд бид дараахь зүйлийг хэлнэ: "нэг" тоонд бид "хасах долоо" гэсэн өөр тоог нэмнэ. Алгебрийн нийлбэр нь энгийн арифметикийн нийлбэрээс ингэж ялгаатай байдаг.
Бүх хувиргалт, нэмэх, үржүүлэх бүрийг хийхдээ дээр дурдсантай ижил төстэй бүтээцүүдийг харж эхэлмэгц олон гишүүнт ба тэгшитгэлтэй ажиллахад алгебрт ямар ч асуудал гарахгүй.
Эцэст нь, бидний саяхан үзсэнээс ч илүү төвөгтэй байх хэд хэдэн жишээг харцгаая, тэдгээрийг шийдэхийн тулд бид стандарт алгоритмаа бага зэрэг өргөжүүлэх хэрэгтэй болно.
Бутархайтай тэгшитгэлийг шийдвэрлэх
Ийм даалгавруудыг шийдвэрлэхийн тулд бид алгоритмдаа нэг алхам нэмэх шаардлагатай болно. Гэхдээ эхлээд алгоритмаа сануулъя:
- Хаалтуудыг нээ.
- Тусдаа хувьсагч.
- Ижил төстэйг нь авчир.
- Харьцаагаар хуваана.
Харамсалтай нь, энэ гайхамшигтай алгоритм нь бүх үр дүнтэй боловч бидний өмнө бутархай байх үед тийм ч тохиромжтой биш юм. Мөн доороос харах зүйлд бид хоёр тэгшитгэлийн зүүн ба баруун талд хоёуланд нь бутархай байна.
Энэ тохиолдолд яаж ажиллах вэ? Тийм ээ, энэ нь маш энгийн! Үүнийг хийхийн тулд та алгоритмд дахин нэг алхам нэмэх хэрэгтэй бөгөөд үүнийг эхний үйлдлээс өмнө болон дараа нь хийж болно, тухайлбал бутархай хэсгүүдээс ангижрах. Тиймээс алгоритм дараах байдалтай байна.
- Бутархай хэсгүүдээс сал.
- Хаалтуудыг нээ.
- Тусдаа хувьсагч.
- Ижил төстэйг нь авчир.
- Харьцаагаар хуваана.
"Бутархайг арилгах" гэдэг нь юу гэсэн үг вэ? Үүнийг яагаад эхний стандарт алхамын дараа болон өмнө хийж болох вэ? Үнэн хэрэгтээ манай тохиолдолд бүх бутархай нь хуваагчдаа тоон шинж чанартай байдаг, i.e. Хаа сайгүй хуваагч нь зүгээр л тоо юм. Иймд тэгшитгэлийн хоёр талыг энэ тоогоор үржүүлбэл бутархай хэсгүүдээс ангижирна.
Жишээ №1
\[\frac(\left(2x+1 \баруун)\left(2x-3 \right))(4)=((x)^(2))-1\]
Энэ тэгшитгэлийн бутархай хэсгүүдээс салцгаая.
\[\frac(\left(2x+1 \баруун)\left(2x-3 \баруун)\cdot 4)(4)=\left(((x)^(2))-1 \баруун)\cdot 4\]
Анхаарна уу: бүгдийг нэг удаа "дөрөв"-өөр үржүүлнэ, өөрөөр хэлбэл. Та хоёр хаалттай байна гэдэг нь тус бүрийг "дөрөв"-өөр үржүүлэх ёстой гэсэн үг биш юм. Ингээд бичье:
\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \баруун)\cdot 4\]
Одоо өргөжүүлье:
Бид хувьсагчийг хасдаг:
Бид ижил төстэй нэр томъёоны бууралтыг гүйцэтгэдэг:
\[-4x=-1\left| :\left(-4 \баруун) \баруун.\]
\[\frac(-4x)(-4)=\frac(-1)(-4)\]
Бид эцсийн шийдлийг хүлээн авлаа, хоёр дахь тэгшитгэл рүү шилжье.
Жишээ №2
\[\frac(\left(1-x \баруун)\зүүн(1+5x \баруун))(5)+(x)^(2))=1\]
Энд бид бүх ижил үйлдлийг гүйцэтгэдэг:
\[\frac(\left(1-x \баруун)\left(1+5x \баруун)\cdot 5)(5)+((x)^(2))\cdot 5=5\]
\[\frac(4x)(4)=\frac(4)(4)\]
Асуудал шийдэгдсэн.
Үнэндээ би өнөөдөр танд хэлэхийг хүссэн зүйл минь энэ.
Гол оноо
Гол дүгнэлтүүд нь:
- Шугаман тэгшитгэлийг шийдвэрлэх алгоритмыг мэдэх.
- Хаалт нээх чадвар.
- Хэрэв та харвал санаа зовох хэрэггүй квадрат функцууд, магадгүй цаашдын өөрчлөлтийн явцад тэдгээр нь буурах болно.
- Шугаман тэгшитгэлд хамгийн энгийн нь ч гэсэн гурван төрлийн язгуур байдаг: нэг язгуур, бүх тооны шугам нь үндэс, огт үндэсгүй.
Энэ хичээл нь бүх математикийг илүү сайн ойлгоход хялбар боловч маш чухал сэдвийг эзэмшихэд тань тусална гэж найдаж байна. Хэрэв ямар нэг зүйл тодорхойгүй байвал сайт руу орж, тэнд үзүүлсэн жишээнүүдийг шийдээрэй. Хамтдаа байгаарай, өөр олон сонирхолтой зүйл таныг хүлээж байна!
 Их Тартар - Оросын эзэнт гүрэн Хүн төрөлхтний эртний түүхийн тухай
Их Тартар - Оросын эзэнт гүрэн Хүн төрөлхтний эртний түүхийн тухай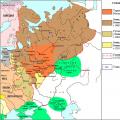 Ханхүү Иван Васильевич 1472 он
Ханхүү Иван Васильевич 1472 он "А.П. Платоновын "Үл мэдэгдэх цэцэг" түүх (бяцхан тойм). Андрей Платоновын "Үл мэдэгдэх цэцэг" өгүүллэгийн тухай "Үл мэдэгдэх цэцэг" жинхэнэ үлгэр надад юу зааж өгсөн бэ?
"А.П. Платоновын "Үл мэдэгдэх цэцэг" түүх (бяцхан тойм). Андрей Платоновын "Үл мэдэгдэх цэцэг" өгүүллэгийн тухай "Үл мэдэгдэх цэцэг" жинхэнэ үлгэр надад юу зааж өгсөн бэ?