Интеграцийн хамгийн чухал шинж чанарууд. Тодорхой бус интегралын үндсэн шинж чанарууд
Функцийг зөвшөөр y = е(x) нь [ интервал дээр тодорхойлогддог. а, б ], а < б. Дараах үйлдлүүдийг хийцгээе.
1) салцгаая [ а, б] цэгүүд а = x 0 < x 1 < ... < x би- 1 < x би < ... < x n = б дээр nхэсэгчилсэн сегментүүд [ x 0 , x 1 ], [x 1 , x 2 ], ..., [x би- 1 , x би ], ..., [x n- 1 , x n ];
2) хэсэгчилсэн сегмент бүрт [ x би- 1 , x би ], би = 1, 2, ... n, дурын цэгийг сонгоод, энэ цэг дэх функцийн утгыг тооцоолно: е(z i ) ;
3) бүтээлүүдийг олох е(z i ) · Δ x би , хэсэгчилсэн сегментийн урт хаана байна [ x би- 1 , x би ], би = 1, 2, ... n;
4) эвлэрье интеграл нийлбэрфункцууд y = е(x) сегмент дээр [ а, б ]:
Геометрийн үүднээс авч үзвэл энэ σ нийлбэр нь суурь нь хэсэгчилсэн сегмент болох тэгш өнцөгтүүдийн талбайн нийлбэр юм. x 0 , x 1 ], [x 1 , x 2 ], ..., [x би- 1 , x би ], ..., [x n- 1 , x n ] ба өндөр нь тэнцүү байна е(z 1 ) , е(z 2 ), ..., е(z n) дагуу (Зураг 1). -ээр тэмдэглэе λ хамгийн урт хэсэгчилсэн сегментийн урт:
5) үед интеграл нийлбэрийн хязгаарыг ол λ → 0.
Тодорхойлолт.Хэрэв интеграл нийлбэрийн (1) хязгаарлагдмал хязгаар байгаа бөгөөд энэ нь сегментийг хуваах аргаас хамаарахгүй бол [ а, б] хэсэгчилсэн сегмент рүү, эсвэл цэгийн сонголтоос z iтэдгээрийн дотор, дараа нь энэ хязгаар гэж нэрлэдэг тодорхой интегралфункцээс y = е(x) сегмент дээр [ а, б] ба тэмдэглэгдсэн байна
Тиймээс,
Энэ тохиолдолд функц е(x) гэж нэрлэдэг нэгтгэх боломжтойдээр [ а, б]. Тоонууд аТэгээд бинтеграцийн доод ба дээд хязгаар гэж нэрлэдэг, е(x) - интеграл функц, е(x ) dx- интеграл илэрхийлэл, x – интеграцийн хувьсагч; шугамын хэсэг [ а, б]-г интеграцийн интервал гэнэ.
Теорем 1.Хэрэв функц бол y = е(x) [ интервал дээр тасралтгүй байна а, б], тэгвэл энэ интервал дээр интегралдах боломжтой.
Интегралын ижил хязгаартай тодорхой интеграл нь тэгтэй тэнцүү байна.
Хэрэв а > б, дараа нь тодорхойлолтоор бид таамаглаж байна
2. Тодорхой интегралын геометрийн утга
Сегмент дээр тавь [ а, б] тасралтгүй сөрөг бус функцийг зааж өгсөн y = е(x ) . Муруй шугаман трапецнь функцийн графикаар хязгаарлагдсан зураг юм y = е(x), доороос - Үхрийн тэнхлэгийн дагуу, зүүн ба баруун тийш - шулуун шугамууд x = aТэгээд x = b(Зураг 2).
Сөрөг бус функцийн тодорхой интеграл y = е(x) геометрийн үүднээс авч үзвэл талбайтай тэнцүүДээрх функцийн графикаар хязгаарлагдсан муруйн трапец y = е(x), зүүн ба баруун - шугамын сегментүүд x = aТэгээд x = b, доороос - Үхрийн тэнхлэгийн сегмент.
3. Тодорхой интегралын үндсэн шинж чанарууд
1. Тодорхой интегралын утга нь интеграцийн хувьсагчийн зориулалтаас хамаарахгүй.
2. Тогтмол коэффициентийг тодорхой интегралын тэмдгээс гаргаж болно.
3. Хоёр функцийн алгебрийн нийлбэрийн тодорхой интеграл нь эдгээр функцүүдийн тодорхой интегралуудын алгебрийн нийлбэртэй тэнцүү байна.
4.If функц y = е(x) нь [ дээр интегралцах боломжтой а, б] Мөн а < б < в, Тэр
5. (дундаж утгын теорем). Хэрэв функц бол y = е(x) [ интервал дээр тасралтгүй байна а, б], тэгвэл энэ сегмент дээр ийм цэг байна
4. Ньютон-Лейбницийн томъёо
Теорем 2.Хэрэв функц бол y = е(x) [ интервал дээр тасралтгүй байна а, б] Мөн Ф(x) нь энэ сегмент дэх түүний эсрэг деривативуудын аль нэг нь байвал дараах томъёо хүчинтэй байна.
гэж нэрлэдэг Ньютон-Лейбницийн томъёо.Ялгаа Ф(б) - Ф(а) нь ихэвчлэн дараах байдлаар бичигддэг.
Энд тэмдгийг давхар орлуулагч тэмдэг гэж нэрлэдэг.
Тиймээс (2) томъёог дараах байдлаар бичиж болно.
Жишээ 1.Интегралыг тооцоолох
Шийдэл. Интегралын хувьд е(x ) = x 2 дурын эсрэг дериватив нь хэлбэртэй байна
Ньютон-Лейбницийн томъёонд аливаа эсрэг деривативыг ашиглаж болох тул интегралыг тооцоолохдоо бид хамгийн энгийн хэлбэртэй эсрэг деривативыг авна.
5. Тодорхой интеграл дахь хувьсагчийн өөрчлөлт
Теорем 3.Функцийг зөвшөөр y = е(x) [ интервал дээр тасралтгүй байна а, б]. Хэрэв:
1) функц x = φ ( т) ба түүний дериватив φ "( т) нь тасралтгүй байна;
2) функцийн утгуудын багц x = φ ( т) нь сегмент нь [ а, б ];
3) φ ( а) = а, φ ( б) = б, тэгвэл томъёо хүчинтэй байна
гэж нэрлэдэг тодорхой интеграл дахь хувьсагчийг өөрчлөх томъёо .
Дургүй тодорхойгүй интеграл, энэ тохиолдолд хэрэгцээгүйанхны интеграцийн хувьсагч руу буцахын тулд α ба β интеграцийн шинэ хязгаарыг олоход л хангалттай (үүнд та хувьсагчийг шийдэх хэрэгтэй. ттэгшитгэл φ ( т) = аба φ ( т) = б).
Орлуулахын оронд x = φ ( т) та орлуулалтыг ашиглаж болно т = g(x). Энэ тохиолдолд хувьсагчийн интеграцийн шинэ хязгаарыг олох болно тхялбарчилна: α = g(а) , β = g(б) .
Жишээ 2. Интегралыг тооцоолох
Шийдэл. Томьёог ашиглан шинэ хувьсагчийг танилцуулъя. Тэгш байдлын хоёр талыг квадрат болгосноор бид 1 + авна x = т 2 , хаана x = т 2 - 1, dx = (т 2 - 1)"dt= 2tdt. Бид интеграцийн шинэ хязгаарыг олж байна. Үүнийг хийхийн тулд хуучин хязгаарыг томъёонд орлъё x = 3 ба x = 8. Бид: , хаанаас авдаг т= 2 ба α = 2; , хаана т= 3 ба β = 3. Тэгэхээр,
Жишээ 3.Тооцоол
Шийдэл. Болъё у= бүртгэл x, Дараа нь, v = x. Томъёоны дагуу (4)
Интегралыг шийдэх нь хялбар ажил боловч зөвхөн сонгогдсон цөөхөн хүмүүст зориулагдсан. Энэ нийтлэл нь интегралуудыг ойлгож сурахыг хүсдэг боловч тэдгээрийн талаар юу ч мэдэхгүй эсвэл бараг юу ч мэдэхгүй хүмүүст зориулагдсан болно. Интеграл... Яагаад хэрэгтэй байна вэ? Үүнийг хэрхэн тооцоолох вэ? Тодорхой ба тодорхойгүй интеграл гэж юу вэ?
Хэрэв интегралын хувьд таны мэддэг цорын ганц хэрэглээ бол хүрэхэд хэцүү газраас хэрэгтэй зүйл авахын тулд салшгүй дүрс хэлбэртэй зүүгээр дэгээ ашиглах явдал юм бол тавтай морилно уу! Математикийн хувьд хамгийн энгийн болон бусад интегралуудыг хэрхэн шийдвэрлэх, яагаад үүнгүйгээр хийж чадахгүй байгааг олж мэдээрэй.
Бид үзэл баримтлалыг судалж байна « интеграл »
Интеграци нь эргээд мэдэгдэж байсан Эртний Египет. Мэдээж орохгүй орчин үеийн хэлбэр, Гэхдээ одоо ч. Түүнээс хойш математикчид энэ сэдвээр олон ном бичсэн. Ялангуяа өөрсдийгөө онцолсон Ньютон Тэгээд Лейбниц , гэхдээ юмсын мөн чанар өөрчлөгдөөгүй.
Интегралыг эхнээс нь хэрхэн ойлгох вэ? Арга ч үгүй! Энэ сэдвийг ойлгохын тулд танд математик анализын үндсэн суурь мэдлэг хэрэгтэй хэвээр байх болно. Манай блог дээр интегралыг ойлгоход шаардлагатай -ын тухай мэдээлэл аль хэдийн бий.
Тодорхой бус интеграл
Бидэнд ямар нэгэн функцтэй байцгаая f(x) .
Тодорхой бус интеграл функц f(x) энэ функцийг дууддаг F(x) , түүний дериватив нь функцтэй тэнцүү байна f(x) .
Өөрөөр хэлбэл интеграл нь урвуу дериватив эсвэл эсрэг дериватив юм. Дашрамд хэлэхэд, хэрхэн яаж хийх талаар манай нийтлэлээс уншина уу.

Бүх тасралтгүй функцүүдэд эсрэг дериватив байдаг. Мөн тогтмол тэмдэгтээр ялгаатай функцүүдийн деривативууд давхцдаг тул эсрэг дериватив дээр тогтмол тэмдэг нэмж өгдөг. Интегралыг олох үйл явцыг интеграл гэж нэрлэдэг.
Энгийн жишээ:

Энгийн функцүүдийн эсрэг деривативуудыг байнга тооцоолохгүйн тулд тэдгээрийг хүснэгтэд оруулж, бэлэн утгыг ашиглах нь тохиромжтой.
Оюутнуудад зориулсан интегралын бүрэн хүснэгт

Тодорхой интеграл
Интеграл гэдэг ойлголттой харьцахдаа бид хязгааргүй жижиг хэмжигдэхүүнтэй харьцаж байна. Интеграл нь зургийн талбай, жигд бус биеийн масс, жигд бус хөдөлгөөний үед туулсан зай болон бусад олон зүйлийг тооцоолоход тусална. Интеграл бол хязгааргүй нийлбэр гэдгийг санах нь зүйтэй их хэмжээнийхязгааргүй жижиг нэр томъёо.
Жишээ болгон зарим функцийн графикийг төсөөлөөд үз дээ.

Функцийн графикаар хязгаарлагдсан дүрсийн талбайг хэрхэн олох вэ? Интеграл ашиглах! Координатын тэнхлэгүүд болон функцийн графикаар хязгаарлагдсан муруй шугаман трапецийг хязгааргүй жижиг хэрчмүүдэд хуваацгаая. Ингэснээр зургийг нимгэн багана болгон хуваах болно. Баганын талбайн нийлбэр нь трапецын талбай болно. Гэхдээ ийм тооцоолол нь ойролцоогоор үр дүнг өгөх болно гэдгийг санаарай. Гэсэн хэдий ч сегментүүд нь жижиг, нарийхан байх тусам тооцоолол илүү нарийвчлалтай болно. Хэрэв бид тэдгээрийг урт нь тэг рүү чиглүүлэх хэмжээгээр багасгах юм бол сегментүүдийн талбайн нийлбэр нь зургийн талбай руу чиглэх болно. Энэ бол тодорхой интеграл бөгөөд үүнийг дараах байдлаар бичсэн болно.

a ба b цэгүүдийг интегралын хязгаар гэж нэрлэдэг.

« Интеграл »
Дашрамд хэлэхэд! Уншигчиддаа зориулж 10% хямдралтай байгаа
Даммигийн интегралыг тооцоолох дүрэм
Тодорхойгүй интегралын шинж чанарууд
Тодорхойгүй интегралыг хэрхэн шийдэх вэ? Энд бид тодорхойгүй интегралын шинж чанаруудыг авч үзэх бөгөөд энэ нь жишээг шийдвэрлэхэд хэрэг болно.
- Интегралын дериватив нь интегралтай тэнцүү байна:

- Тогтмолыг интеграл тэмдгийн доороос гаргаж болно.

- Нийлбэрийн интеграл нь интегралын нийлбэртэй тэнцүү байна. Энэ нь мөн ялгааны хувьд үнэн юм:
Тодорхой интегралын шинж чанарууд
- Шугаман чанар:

- Интегралын хязгаарыг сольсон тохиолдолд интегралын тэмдэг өөрчлөгдөнө.

- At ямар чоноо а, бТэгээд -тай:

Тодорхой интеграл нь нийлбэрийн хязгаар гэдгийг бид аль хэдийн олж мэдсэн. Гэхдээ жишээг шийдэхдээ тодорхой утгыг хэрхэн авах вэ? Үүний тулд Ньютон-Лейбницийн томъёо байдаг:

Интегралыг шийдвэрлэх жишээ
Доор бид тодорхойгүй интеграл болон шийдлийн жишээг авч үзэх болно. Бид танд шийдлийн нарийн ширийнийг өөрөө олж мэдэхийг санал болгож байна, хэрэв ямар нэг зүйл тодорхойгүй байвал сэтгэгдэл дээр асуулт асуугаарай.

Материалыг бататгахын тулд интегралыг практикт хэрхэн шийддэг тухай видеог үзээрэй. Хэрэв интегралыг шууд өгөхгүй бол цөхрөл бүү зов. Оюутнуудад зориулсан мэргэжлийн үйлчилгээтэй холбоо бариарай, битүү гадаргуу дээрх гурвалсан эсвэл муруй интеграл нь таны хүчин чадалд багтах болно.
Эдгээр шинж чанарууд нь интегралыг энгийн интегралуудын аль нэгэнд нь буулгах, цаашдын тооцоололд шилжүүлэхэд ашиглагддаг.
1. Тодорхой бус интегралын дериватив нь интегралтай тэнцүү байна.
2. Тодорхой бус интегралын дифференциал нь интегралтай тэнцүү байна.
3. Тодорхой функцийн дифференциалын тодорхойгүй интеграл нь энэ функц ба дурын тогтмолын нийлбэртэй тэнцүү байна.
4. Тогтмол коэффициентийг интеграл тэмдэгээс гаргаж болно.
Үүнээс гадна, a ≠ 0
5. Нийлбэрийн интеграл (ялгаа) нь интегралуудын нийлбэртэй (ялгаатай) тэнцүү байна.
6. Үл хөдлөх хөрөнгө нь 4 ба 5-р шинж чанаруудын нэгдэл юм:
Түүнчлэн, a ≠ 0 ˄ b ≠ 0
7. Тодорхой бус интегралын хувьсах шинж чанар:
Хэрэв бол
8. Эд хөрөнгө:
Хэрэв бол
Үнэн хэрэгтээ энэ өмч нь хувьсагчийг өөрчлөх аргыг ашиглан интеграцийн онцгой тохиолдол бөгөөд дараагийн хэсэгт илүү дэлгэрэнгүй авч үзэх болно.
Нэг жишээг харцгаая:
Эхлээд бид шинж чанар 5, дараа нь шинж чанар 4, дараа нь бид эсрэг деривативын хүснэгтийг ашиглаж, үр дүнг авсан.
Манай онлайн интеграл тооцоолуурын алгоритм нь дээр дурдсан бүх шинж чанарыг дэмждэг бөгөөд таны интегралын нарийвчилсан шийдлийг хялбархан олох болно.
Энэ нийтлэлд тодорхой интегралын үндсэн шинж чанаруудын талаар дэлгэрэнгүй ярих болно. Тэдгээрийг Риманн ба Дарбоусын интегралын үзэл баримтлалыг ашиглан нотолсон. Тодорхой интегралыг тооцоолох нь 5 шинж чанарын ачаар явагддаг. Үлдсэнийг нь янз бүрийн илэрхийллийг үнэлэхэд ашигладаг.
Тодорхой интегралын үндсэн шинж чанарууд руу шилжихийн өмнө a-аас b-ээс хэтрэхгүй эсэхийг шалгах шаардлагатай.
Тодорхой интегралын үндсэн шинж чанарууд
Тодорхойлолт 1x = a дээр тодорхойлсон y = f (x) функц нь шударга тэгш байдал ∫ a a f (x) d x = 0-тэй төстэй.
Нотлох баримт 1
Эндээс бид хязгаартай давхцах интегралын утга тэгтэй тэнцүү болохыг харж байна. Энэ нь Риманы интегралын үр дагавар бөгөөд учир нь [ a ; a ] ба ζ i цэгүүдийн дурын сонголт тэгтэй тэнцүү, учир нь x i - x i - 1 = 0 , i = 1 , 2 , . . . , n , энэ нь бид интеграл функцүүдийн хязгаар тэг болохыг олж мэдсэн гэсэн үг юм.
Тодорхойлолт 2
[a; интервал дээр интегралдах функцийн хувьд; b ] , ∫ a b f (x) d x = - ∫ b a f (x) d x нөхцөл биелэгдэнэ.
Нотлох баримт 2
Өөрөөр хэлбэл интегралын дээд доод хязгаарыг сольвол интегралын утга эсрэг утгатай болж өөрчлөгдөнө. Энэ өмчРиманы интегралаас авсан. Гэхдээ сегментийн хуваалтыг дугаарлах нь x = b цэгээс эхэлдэг.
Тодорхойлолт 3
∫ a b f x ± g (x) d x = ∫ a b f (x) d x ± ∫ a b g (x) d x нь [ a интервал дээр тодорхойлогдсон y = f (x) ба y = g (x) төрлийн интегралдах функцүүдэд хамаарна; b ].
Нотлох баримт 3
Өгөгдсөн ζ i цэгийн сонголттой сегментүүдэд хуваахад y = f (x) ± g (x) функцийн интеграл нийлбэрийг бичнэ үү: σ = ∑ i = 1 n f ζ i ± g ζ i · x i - x i - 1 = = ∑ i = 1 n f (ζ i) · x i - x i - 1 ± ∑ i = 1 n g ζ i · x i - x i - 1 = σ f ± σ g
Энд σ f ба σ g нь сегментийг хуваахад y = f (x) ба y = g (x) функцүүдийн салшгүй нийлбэр юм. λ = m a x i = 1, 2, үед хязгаарт хүрсэний дараа. . . , n (x i - x i - 1) → 0 нь lim λ → 0 σ = lim λ → 0 σ f ± σ g = lim λ → 0 σ g ± lim λ → 0 σ g болохыг олж авна.
Риманы тодорхойлолтоос харахад энэ илэрхийлэл тэнцүү байна.
Тодорхойлолт 4
Тогтмол хүчин зүйлийг тодорхой интегралын тэмдгээс цааш сунгах. интервалаас нэгдсэн функц [a; b ] дурын утгатай k нь ∫ a b k · f (x) d x = k · ∫ a b f (x) d x хэлбэрийн шударга тэгш бус байдалтай байна.
Баталгаа 4
Тодорхой салшгүй өмчийн нотолгоо нь өмнөхтэй төстэй байна.
σ = ∑ i = 1 n k · f ζ i · (x i - x i - 1) = = k · ∑ i = 1 n f ζ i · (x i - x i - 1) = k · σ f ⇒ lim λ → 0 σ = lim λ → 0 (k · σ f) = k · lim λ → 0 σ f ⇒ ∫ a b k · f (x) d x = k · ∫ a b f (x) d x
Тодорхойлолт 5
Хэрэв y = f (x) хэлбэрийн функц нь ∈ x, b ∈ x интервал дээр интегралдах боломжтой бол ∫ a b f (x) d x = ∫ a c f (x) d x + ∫ c b f (x) d болохыг олж авна. x.
Нотлох баримт 5
Энэ үл хөдлөх хөрөнгийг c ∈ a-д хүчинтэй гэж үзнэ; b, c ≤ a ба c ≥ b-ийн хувьд. Нотолгоо нь өмнөх шинж чанаруудтай төстэй юм.
Тодорхойлолт 6
Функцийг сегментээс интегралдах боломжтой үед [a; b ], тэгвэл энэ нь ямар ч дотоод сегментэд боломжтой c; d ∈ a ; б.
Баталгаа 6
Нотолгоо нь Darboux шинж чанар дээр суурилдаг: хэрвээ сегментийн одоо байгаа хэсэг дээр цэг нэмбэл доод Darboux нийлбэр буурахгүй, дээд хэсэг нь нэмэгдэхгүй.
Тодорхойлолт 7
Функц нь [a; b ] -аас f (x) ≥ 0 f (x) ≤ 0 дурын утгын х ∈ a ; b , тэгвэл бид ∫ a b f (x) d x ≥ 0 ∫ a b f (x) ≤ 0 болно.
Энэ шинж чанарыг Риманы интегралын тодорхойлолтыг ашиглан баталж болно: f (x) ≥ 0 f (x) ≤ 0 нь сөрөг биш байх нөхцөлтэй сегментийн хуваах цэг ба ζ i цэгүүдийн дурын интеграл нийлбэр. .
Нотлох баримт 7
Хэрэв y = f (x) ба y = g (x) функцууд нь [ a ; b ] байвал дараах тэгш бус байдлыг хүчинтэй гэж үзнэ.
∫ a b f (x) d x ≤ ∫ a b g (x) d x , f (x) ≤ g (x) ∀ x ∈ a ; b ∫ a b f (x) d x ≥ ∫ a b g (x) d x , f (x) ≥ g (x) ∀ x ∈ a ; б
Мэдэгдэлийн ачаар интеграцчлалыг зөвшөөрч болохыг бид мэднэ. Энэ үр дүнг бусад шинж чанарыг нотлоход ашиглана.
Тодорхойлолт 8
Интегралдах функцийн хувьд y = f (x) интервалаас [ a ; b ] бидэнд ∫ a b f (x) d x ≤ ∫ a b f (x) d x хэлбэрийн тэгш бус байдал байна.
Баталгаа 8
Бидэнд байгаа - f (x) ≤ f (x) ≤ f (x) . Өмнөх шинж чанараас бид тэгш бус байдлыг гишүүнээр нь нэгтгэж болох бөгөөд энэ нь - ∫ a b f (x) d x ≤ ∫ a b f (x) d x ≤ ∫ a b f (x) d x хэлбэрийн тэгш бус байдалд тохирч байгааг олж мэдсэн. Энэ давхар тэгш бус байдлыг өөр хэлбэрээр бичиж болно: ∫ a b f (x) d x ≤ ∫ a b f (x) d x .
Тодорхойлолт 9
y = f (x) ба y = g (x) функцууд [ a ; b ] ямар ч x ∈ a хувьд g (x) ≥ 0; b , бид m · ∫ a b g (x) d x ≤ ∫ a b f (x) · g (x) d x ≤ M · ∫ a b g (x) d x хэлбэрийн тэгш бус байдлыг олж авна, энд m = m i n x ∈ a ; b f (x) ба M = m a x x ∈ a ; b f (x) .
Нотлох баримт 9
Нотолгоо нь ижил төстэй байдлаар хийгддэг. M ба m нь [a сегментээс тодорхойлсон y = f (x) функцийн хамгийн том ба хамгийн бага утгууд гэж тооцогддог; b ] , дараа нь m ≤ f (x) ≤ M . Давхар тэгш бус байдлыг y = g (x) функцээр үржүүлэх шаардлагатай бөгөөд энэ нь m g (x) ≤ f (x) g (x) ≤ M g (x) хэлбэрийн давхар тэгш бус байдлын утгыг өгнө. Үүнийг интервал дээр нэгтгэх шаардлагатай [a; b ] , тэгвэл бид нотлох мэдэгдлийг авна.
Үр дагавар: g (x) = 1-ийн хувьд тэгш бус байдал нь m · b - a ≤ ∫ a b f (x) d x ≤ M · (b - a) хэлбэртэй байна.
Эхний дундаж томъёо
Тодорхойлолт 10y = f (x) интервал дээр интегралдах [ a ; b ] -тэй m = m i n x ∈ a ; b f (x) ба M = m a x x ∈ a ; b f (x) μ ∈ m тоо байна; ∫ a b f (x) d x = μ · b - a -д тохирох M .
Үр дагавар: y = f (x) функц нь [ a интервалаас тасралтгүй байх үед ; b ], тэгвэл c ∈ a тоо байна; b, тэгш байдлыг хангасан ∫ a b f (x) d x = f (c) b - a.
Эхний дундаж томьёо ерөнхий хэлбэрээр
Тодорхойлолт 11y = f (x) ба y = g (x) функцууд нь [ a ; b ] -тэй m = m i n x ∈ a ; b f (x) ба M = m a x x ∈ a ; b f (x) , ба ямар ч утгын хувьд g (x) > 0 x ∈ a ; б. Эндээс бид μ ∈ m гэсэн тоо байна; ∫ a b f (x) · g (x) d x = μ · ∫ a b g (x) d x тэгшитгэлийг хангасан M .
Хоёр дахь дундаж томъёо
Тодорхойлолт 12y = f (x) функц нь [ a ; b ] ба y = g (x) нь монотон, тэгвэл c ∈ a гэсэн тоо байна; b , энд ∫ a b f (x) · g (x) d x = g (a) · ∫ a c f (x) d x + g (b) · ∫ c b f (x) d x хэлбэрийн шударга тэгш байдлыг олж авна.
Хэрэв та текстэнд алдаа байгааг анзаарсан бол үүнийг тодруулаад Ctrl+Enter дарна уу
Эсрэг дериватив функц ба тодорхойгүй интеграл
Баримт 1. Интеграл гэдэг нь дифференциалын урвуу үйлдэл, тухайлбал, энэ функцийн мэдэгдэж буй деривативаас функцийг сэргээх явдал юм. Ингэснээр функц сэргээгдсэн Ф(x) гэж нэрлэдэг эсрэг деривативфункцийн хувьд е(x).
Тодорхойлолт 1. Чиг үүрэг Ф(x е(x) тодорхой интервалаар X, хэрэв бүх утгын хувьд xЭнэ интервалаас тэгш байдал хадгалагдана Ф "(x)=е(x), өөрөөр хэлбэл энэ функц е(x) нь эсрэг дериватив функцийн дериватив юм Ф(x). .
Жишээлбэл, функц Ф(x) = нүгэл x функцийн эсрэг дериватив юм е(x) = cos x бүх тооны шулуун дээр, учир нь x-ийн дурын утгын хувьд (нүгэл x)" = (cos x) .
Тодорхойлолт 2. Функцийн тодорхойгүй интеграл е(x) нь түүний бүх эсрэг деривативуудын багц юм. Энэ тохиолдолд тэмдэглэгээг ашиглана
∫
е(x)dx
,тэмдэг хаана байна ∫ интеграл тэмдэг, функц гэж нэрлэдэг е(x) – интеграл функц, ба е(x)dx - интеграл илэрхийлэл.
Тиймээс, хэрэв Ф(x) – зарим эсрэг дериватив е(x), Тэр
∫
е(x)dx = Ф(x) +C
Хаана C - дурын тогтмол (тогтмол).
Функцийн эсрэг деривативуудын багцын утгыг тодорхойгүй интеграл гэж ойлгохын тулд дараах зүйрлэл тохиромжтой. Хаалга (уламжлалт модон хаалга) байг. Үүний үүрэг бол "хаалга байх" юм. Хаалга юугаар хийгдсэн бэ? Модоор хийгдсэн. Энэ нь "хаалга байх" функцийн интегралын эсрэг деривативуудын олонлог, өөрөөр хэлбэл түүний тодорхойгүй интеграл нь "мод байх + C" функц байна гэсэн үг бөгөөд C нь тогтмол бөгөөд энэ нөхцөлд үүнийг хийж болно. жишээлбэл, модны төрлийг заана. Хаалгыг зарим багаж ашиглан модоор хийдэгтэй адил функцийн деривативыг ашиглан эсрэг дериватив функцээс "бүтээдэг". деривативыг судалж байхдаа бидний сурсан томъёо .
Дараа нь нийтлэг объектуудын функцын хүснэгт ба тэдгээрийн харгалзах эсрэг деривативууд ("хаалга байх" - "мод байх", "халбага байх" - "төмөр байх" гэх мэт) нь үндсэн хүснэгттэй төстэй байна. тодорхойгүй интегралуудыг доор өгөв. Тодорхой бус интегралын хүснэгтэд эдгээр функцийг "хийсэн" эсрэг деривативуудыг харуулсан нийтлэг функцуудыг жагсаав. Тодорхой бус интегралыг олох асуудлын нэг хэсэгт маш их хүчин чармайлтгүйгээр шууд интегралд оруулах боломжтой, өөрөөр хэлбэл тодорхойгүй интегралын хүснэгтийг ашиглан интегралуудыг өгдөг. Илүү төвөгтэй бодлогод хүснэгтийн интегралыг ашиглахын тулд эхлээд интегралыг хувиргах ёстой.
Баримт 2. Функцийг эсрэг дериватив болгон сэргээхдээ бид дурын тогтмол (тогтмол)-ыг харгалзан үзэх ёстой. C, мөн 1-ээс хязгааргүй хүртэлх янз бүрийн тогтмолтой эсрэг деривативуудын жагсаалтыг бичихгүйн тулд дурын тогтмолтой эсрэг деривативуудын багц бичих хэрэгтэй. C, жишээ нь: 5 x³+C. Тиймээс эсрэг дериватив нь функц байж болох тул дурын тогтмол (тогтмол) нь эсрэг деривативын илэрхийлэлд багтсан болно, жишээлбэл, 5. x³+4 эсвэл 5 x³+3, ялгах үед 4 эсвэл 3 эсвэл бусад тогтмол нь тэг болно.
Энэ функцийн хувьд интеграцийн асуудлыг тавьцгаая е(x) ийм функцийг ол Ф(x), хэний деривативтэнцүү е(x).
Жишээ 1.Функцийн эсрэг деривативуудын олонлогийг ол
Шийдэл. Энэ функцийн хувьд эсрэг дериватив нь функц юм
Чиг үүрэг Ф(x) функцийн эсрэг дериватив гэж нэрлэдэг е(x), хэрэв дериватив бол Ф(x) тэнцүү байна е(x), эсвэл ижил зүйл болох дифференциал Ф(x) тэнцүү байна е(x) dx, өөрөөр хэлбэл
![]() (2)
(2)
Тиймээс функц нь функцийн эсрэг дериватив юм. Гэсэн хэдий ч энэ нь цорын ганц эсрэг дериватив биш юм. Тэд бас үүрэг гүйцэтгэдэг
Хаана ХАМТ- дурын тогтмол. Үүнийг ялгах замаар баталгаажуулж болно.
Тиймээс, хэрэв функцэд нэг эсрэг дериватив байвал түүний хувьд тогтмол гишүүнээр ялгаатай хязгааргүй тооны эсрэг дериватив байдаг. Функцийн бүх эсрэг деривативуудыг дээрх хэлбэрээр бичнэ. Энэ нь дараах теоремоос үүдэлтэй.
Теорем (баримт 2-ын албан ёсны мэдэгдэл).Хэрэв Ф(x) – функцийн эсрэг дериватив е(x) тодорхой интервалаар X, дараа нь бусад ямар ч эсрэг дериватив е(x) ижил интервал дээр хэлбэрээр илэрхийлж болно Ф(x) + C, Хаана ХАМТ- дурын тогтмол.
Дараагийн жишээнд бид тодорхойгүй интегралын шинж чанаруудын дараа 3-р зүйлд өгөгдсөн интегралын хүснэгт рүү шилждэг. Дээрх зүйлийн мөн чанар тодорхой байхын тулд бид хүснэгтийг бүхэлд нь уншихаас өмнө үүнийг хийдэг. Хүснэгт болон шинж чанаруудын дараа бид нэгтгэх явцад тэдгээрийг бүхэлд нь ашиглах болно.
Жишээ 2.Эсрэг дериватив функцүүдийн багцыг ол:
Шийдэл. Бид эдгээр функцийг "хийсэн" эсрэг дериватив функцүүдийн багцыг олдог. Интегралын хүснэгтээс томъёог дурдахдаа одоохондоо ийм томьёо байдаг гэдгийг хүлээн зөвшөөрч, тодорхой бус интегралын хүснэгтийг өөрөө бага зэрэг судлах болно.
1) Интегралын хүснэгтээс (7) томъёог ашиглана n= 3, бид олж авна
![]()
2) Интегралын хүснэгтээс (10) томъёог ашиглана n= 1/3, бидэнд байна
3) Түүнээс хойш
дараа нь (7) томъёоны дагуу n= -1/4 бид олдог
![]()
Энэ нь интеграл тэмдгийн доор бичигдсэн функц өөрөө биш юм. е, мөн түүний бүтээгдэхүүн нь дифференциалаар dx. Энэ нь үндсэндээ эсрэг деривативыг аль хувьсагчаар хайж байгааг харуулахын тулд хийгддэг. Жишээлбэл,
![]() ,
,
![]() ;
;
Энд хоёр тохиолдолд интеграл нь -тэй тэнцүү боловч авч үзсэн тохиолдолд түүний тодорхойгүй интегралууд өөр байна. Эхний тохиолдолд энэ функцийг хувьсагчийн функц гэж үзнэ x, хоёрдугаарт - функцээр z .
Функцийн тодорхойгүй интегралыг олох үйл явцыг тухайн функцийг интегралдах гэж нэрлэдэг.
Тодорхой бус интегралын геометрийн утга
Бид муруй олох хэрэгтэй гэж бодъё y=F(x)Мөн түүний цэг тус бүрийн шүргэгч өнцгийн тангенс нь өгөгдсөн функц гэдгийг бид аль хэдийн мэдсэн f(x)энэ цэгийн абсцисса.
Деривативын геометрийн утгын дагуу муруйн өгөгдсөн цэг дэх шүргэгчийн налуу өнцгийн тангенс y=F(x)деривативын утгатай тэнцүү байна F"(x). Тиймээс бид ийм функцийг олох хэрэгтэй F(x), Үүний төлөө F"(x)=f(x). Даалгаварт шаардлагатай функц F(x)-ийн эсрэг дериватив юм f(x). Асуудлын нөхцлийг нэг муруй биш, харин муруйн гэр бүл хангадаг. y=F(x)- эдгээр муруйнуудын аль нэгийг, мөн өөр ямар ч муруйг тэнхлэгийн дагуу параллель хөрвүүлэх замаар олж авч болно Өө.
-ийн эсрэг дериватив функцийн графикийг нэрлэе f(x)интеграл муруй. Хэрэв F"(x)=f(x), дараа нь функцийн график y=F(x)интеграл муруй байна.
Баримт 3. Тодорхой бус интеграл нь геометрийн хувьд бүх интеграл муруйн бүлгээр илэрхийлэгдэнэ. , доорх зурган дээрх шиг. Муруй бүрийн координатын гарал үүслийн зайг дурын интеграцийн тогтмолоор тодорхойлно C.

Тодорхойгүй интегралын шинж чанарууд
Баримт 4. Теорем 1. Тодорхой бус интегралын дериватив нь интегралтай, дифференциал нь интегралтай тэнцүү.
Баримт 5. Теорем 2. Функцийн дифференциалын тодорхойгүй интеграл е(x) функцтэй тэнцүү байна е(x) тогтмол хугацаа хүртэл , өөрөөр хэлбэл
![]() (3)
(3)
1 ба 2-р теоремууд нь дифференциал ба интеграл нь харилцан урвуу үйлдлүүд гэдгийг харуулж байна.
Баримт 6. Теорем 3. Интеграл дахь тогтмол хүчин зүйлийг тодорхойгүй интегралын тэмдгээс гаргаж авч болно. , өөрөөр хэлбэл
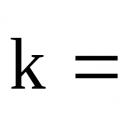 Урвалын хурдны тогтмол Лабораторийн ажлын удирдамж
Урвалын хурдны тогтмол Лабораторийн ажлын удирдамж Үхлийн дараах амьдрал бий юу?
Үхлийн дараах амьдрал бий юу? Эрдэмтэд: Дэлхий бол хүн төрөлхтний "сансрын шорон" Эрдэмтэд: Дэлхий бол сансрын шорон
Эрдэмтэд: Дэлхий бол хүн төрөлхтний "сансрын шорон" Эрдэмтэд: Дэлхий бол сансрын шорон