Қалыпты таралу және оның параметрлері. Ықтималдық үлестірудің қалыпты заңы Қалыпты үлестіруді қандай параметрлер сипаттайды
Қалыпты таралған кездейсоқ шамаларға байланысты көптеген есептер кезінде -ден -ге дейінгі кесіндіге түсетін, параметрлері бар қалыпты заңға бағынатын кездейсоқ шаманың ықтималдығын анықтау қажет. Бұл ықтималдықты есептеу үшін біз жалпы формуланы қолданамыз
мұндағы шаманың үлестіру функциясы.
Параметрлері бар қалыпты заң бойынша бөлінген кездейсоқ шаманың таралу функциясын табайық. Мәннің таралу тығыздығы мынаған тең:
Осыдан таралу функциясын табамыз
 . (6.3.3)
. (6.3.3)
(6.3.3) интегралда айнымалыға өзгеріс енгізейік.
және оны мына пішінге келтірейік:
 (6.3.4)
(6.3.4)
Интеграл (6.3.4) элементар функциялар арқылы өрнектелмейді, бірақ оны өрнектейтін арнайы функция арқылы есептеуге болады. анықталған интегралкестелер құрастырылған өрнектен немесе (ықтималдық интегралы деп аталады). Мұндай функциялардың көптеген түрлері бар, мысалы:
 ;
;

және т.б. Осы функциялардың қайсысын пайдалану талғамға байланысты. Біз осындай функция ретінде таңдаймыз
 . (6.3.5)
. (6.3.5)
Бұл функцияның параметрлері бар қалыпты таралған кездейсоқ шама үшін тарату функциясынан басқа ештеңе емес екенін түсіну оңай.
Функцияны қалыпты таралу функциясы деп атауға келейік. Қосымшада (1-кесте) функция мәндерінің кестелері бар.
Шаманың таралу функциясын (6.3.3) параметрлермен және қалыпты таралу функциясы арқылы өрнектейік. Әлбетте,
Енді -ден -ге дейінгі кесіндіге кездейсоқ шаманың түсу ықтималдығын табайық. (6.3.1) формулаға сәйкес
Осылайша, кез келген параметрлері 0,1 параметрлері бар қарапайым қалыпты заңға сәйкес келетін стандартты үлестіру функциясы арқылы бөлімге түсетін қалыпты заң бойынша бөлінген кездейсоқ шаманың ықтималдығын өрнектедік. (6.3.7) формуладағы функция аргументтері өте қарапайым мағынаға ие екенін ескеріңіз: бөлімнің оң жақ шетінен шашырау центріне дейінгі қашықтық стандартты ауытқулармен көрсетілген; - қиманың сол жақ шеті үшін бірдей қашықтық және бұл қашықтық егер ұшы дисперсия центрінің оң жағында орналасса оң, ал сол жақта болса теріс болып саналады.
Кез келген тарату функциясы сияқты функцияның келесі қасиеттері бар:
3. - кемімейтін функция.
Сонымен қатар, басына қатысты параметрлері бар қалыпты таралудың симметриясынан мынандай нәтиже шығады
Бұл сипатты пайдалану, нақты айтқанда, функционалдық кестелерді тек оң аргумент мәндерімен шектеуге болады, бірақ қажетсіз операцияны болдырмау үшін (бірден алу) 1-кестеде оң және теріс аргументтердің мәндері берілген.

Тәжірибеде біз қалыпты таралған кездейсоқ шаманың шашырау центріне қатысты симметриялы аймаққа түсу ықтималдығын есептеу мәселесімен жиі кездесеміз. Ұзындықтың мұндай қимасын қарастырайық (6.3.1-сурет). (6.3.7) формула арқылы осы аймаққа соғу ықтималдығын есептейік:
Функцияның (6.3.8) қасиетін ескере отырып және (6.3.9) формуланың сол жағын неғұрлым ықшам түр бере отырып, қалыпты заң бойынша бөлінген кездейсоқ шама ықтималдығының формуласын аламыз. шашырау центріне қатысты симметриялы аудан:
![]() .
(6.3.10)
.
(6.3.10)
Келесі есепті шешейік. Дисперсиялық центрден ұзындықтың дәйекті кесінділерін салайық (6.3.2-сурет) және олардың әрқайсысына кездейсоқ шаманың түсу ықтималдығын есептейік. Қалыпты қисық симметриялы болғандықтан, мұндай кесінділерді тек бір бағытта салу жеткілікті.

Формула (6.3.7) арқылы табамыз:
 (6.3.11)
(6.3.11)
Осы мәліметтерден көрініп тұрғандай, 0,001 дәлдікпен келесі сегменттердің (бесінші, алтыншы және т.б.) әрқайсысына соғу ықтималдығы нөлге тең.
Сегменттерге кіру ықтималдығын 0,01-ге (1% дейін) дөңгелектесек, біз есте сақтау оңай үш сан аламыз:
0,34; 0,14; 0,02.
Осы үш мәннің қосындысы 0,5-ке тең. Бұл қалыпты үлестірілген кездейсоқ шама үшін барлық дисперсия (пайыз үлестерінің дәлдігімен) ауданға сәйкес келетінін білдіреді.
Бұл кездейсоқ шаманың стандартты ауытқуы мен математикалық күтуін біле отырып, оның іс жүзінде мүмкін болатын мәндерінің ауқымын шамамен көрсетуге мүмкіндік береді. Кездейсоқ шаманың мүмкін мәндерінің ауқымын бағалаудың бұл әдісі белгілі математикалық статистика«үш сигма ережесі» деп аталады. Үш сигма ережесі кездейсоқ шаманың стандартты ауытқуын анықтаудың жуық әдісін де білдіреді: орташа мәннен іс жүзінде мүмкін болатын максималды ауытқуды алыңыз және оны үшке бөліңіз. Әрине, бұл өрескел әдісті анықтаудың басқа, дәлірек әдістері болмаса ғана ұсынуға болады.
Мысал 1. Қалыпты заң бойынша бөлінген кездейсоқ шама белгілі бір қашықтықты өлшеудегі қатені білдіреді. Өлшеу кезінде 1,2 (м) артық бағалау бағытында жүйелі қателікке жол беріледі; Өлшеу қателігінің стандартты ауытқуы 0,8 (м) құрайды. Өлшенетін шаманың ақиқат мәннен ауытқуы абсолютті шамада 1,6 (м) аспау ықтималдығын табыңыз.
Шешім. Өлшеу қатесі - және параметрлері бар қалыпты заңға бағынатын кездейсоқ шама. Бұл шаманың -ден -ге дейінгі кесіндіге түсу ықтималдығын табу керек. (6.3.7) формулаға сәйкес бізде:
Функционалдық кестелерді (Қосымша, 1-кесте) пайдалана отырып, біз табамыз:
![]() ;
,
;
,
Мысал 2. Алдыңғы мысалдағыдай ықтималдықты табыңыз, бірақ жүйелі қате болмаса.
Шешім. (6.3.10) формуласын қолданып, деп алсақ, мынаны табамыз:
Мысал 3. Ені 20 м болатын жолақ (автомобиль жолы) тәрізді нысана тас жолға перпендикуляр бағытта атылады. Мақсаттау тас жолдың орталық сызығы бойынша жүзеге асырылады. Түсіру бағытында стандартты ауытқу м-ге тең.Ату бағытында жүйелі қателік бар: астыңғы қашу 3 м.Бір оқпен тас жолға соғу ықтималдығын табыңыз.
Ықтималдықтар теориясында ең танымал және жиі қолданылатын заң қалыпты таралу заңы немесе Гаусс заңы .
негізгі ерекшелігіқалыпты таралу заңы - бұл түпкілікті заңбасқа тарату заңдары үшін.
Қалыпты үлестіру үшін интегралдық функция келесідей болатынын ескеріңіз:
 .
.
Енді көрсетейікпараметрлердің ықтималдық мәні келесідей: А математикалық күту, - қалыпты үлестірімнің стандартты ауытқуы (яғни):
а) үздіксіз кездейсоқ шаманың математикалық күтуінің анықтамасы бойынша бізде бар

Шынымен
 ,
,
өйткені интегралдық таңбаның астында бар тақ функция, ал интегралдау шекаралары координаттар басына қатысты симметриялы;
 - Пуассон интегралы .
- Пуассон интегралы .
Сонымен, қалыпты үлестірудің математикалық күтуі параметрге тең А .
б) үзіліссіз кездейсоқ шаманың дисперсиясын анықтау арқылы және мынаны ескере отырып, жаза аламыз
 .
.
Бөлшектері бойынша біріктіру, қою  , табайық
, табайық

Демек ![]() .
.
Сонымен, қалыпты таралудың стандартты ауытқуы параметрге тең.
 |
Жағдайда және қалыпты таралунормаланған (немесе стандартты қалыпты) таралу деп аталады. Сонда, анық, нормаланған тығыздық (дифференциалдық) және нормаланған интегралдық үлестіру функциясы сәйкесінше келесі түрде жазылады:

(Функция, өздеріңіз білетіндей, Лаплас функциясы (5 ДӘРІСТІ қараңыз) немесе ықтималдық интегралы деп аталады. Екі функция да, яғни ![]() , кестеленген және олардың мәндері сәйкес кестелерде жазылған).
, кестеленген және олардың мәндері сәйкес кестелерде жазылған).
Қалыпты таралу қасиеттері (қалыпты қисықтың қасиеттері):
1. Бүкіл сан түзуіндегі функция екені анық.
2. ![]() , яғни қалыпты қисық осьтің үстінде орналасқан О
.
, яғни қалыпты қисық осьтің үстінде орналасқан О
.
3. ![]() , яғни ось О
графиктің көлденең асимптотасы қызметін атқарады.
, яғни ось О
графиктің көлденең асимптотасы қызметін атқарады.
4. Қалыпты қисық түзуге қатысты симметриялы x = a (сәйкесінше, функцияның графигі оське қатысты симметриялы OU ).
Сондықтан біз жаза аламыз: .
5.  .
.
6. Ұпайларды көрсету оңай  Және
Және  қалыпты қисықтың иілу нүктелері болып табылады (оны өзіңіз дәлелдеңіз).
қалыпты қисықтың иілу нүктелері болып табылады (оны өзіңіз дәлелдеңіз).
7.Ол анық

бірақ бері  , Бұл
, Бұл ![]() . Сонымен қатар
. Сонымен қатар ![]() , демек, барлық тақ моменттері нөлге тең.
, демек, барлық тақ моменттері нөлге тең.
Бір сәтке біз жаза аламыз:

8.  .
.
9.  .
.
10. ![]() , Қайда.
, Қайда.
11. Кездейсоқ шаманың теріс мәндері үшін: , мұндағы .
13. Кездейсоқ шаманың таралу центріне қатысты симметриялы қимаға түсу ықтималдығы мынаған тең:

МЫСАЛ 3. Қалыпты таралған кездейсоқ шама екенін көрсетіңіз X математикалық күтуден ауытқиды М(X) артық емес.
Шешім. Қалыпты таралу үшін: ![]() .
.

Басқаша айтқанда, ауытқудың абсолютті мәнінің ықтималдығы асып түседіүш еселенген стандартты ауытқу өте аз, атап айтқанда 0,0027-ге тең.Бұл тек 0,27% жағдайда ғана болуы мүмкін дегенді білдіреді. Болмайтын оқиғалардың мүмкін еместігі принципіне негізделген мұндай оқиғаларды іс жүзінде мүмкін емес деп санауға болады.
Сонымен, 0,9973 ықтималдығы бар оқиғаны іс жүзінде сенімді деп санауға болады, яғни кездейсоқ шама математикалық күтуден -ден көп емес ауытқиды.
МЫСАЛ 4. Кездейсоқ шаманың қалыпты таралу сипаттамаларын білу X - болаттың созылу беріктігі: кг/мм2 және кг/мм2, созылу беріктігі 31кг/мм2-ден 35кг/мм2-ге дейінгі болат алу ықтималдығын табыңыз.
Шешім.
3. Көрсеткіштік үлестірім (көрсеткіштік үлестірім заңы)
 |
Экспоненциалды – үздіксіз кездейсоқ шаманың ықтималдық үлестірімі. X , ол дифференциалдық функциямен сипатталады (тарату тығыздығы)

мұндағы тұрақты оң мән.
Көрсеткіштік үлестірім анықталған бірпараметр. Экспоненциалды үлестірімнің бұл ерекшелігі оның параметрдің көп санына тәуелді үлестіріммен салыстырғанда артықшылығын көрсетеді. Әдетте параметрлер белгісіз және олардың бағалауын (шамамен мәндерін) табуға тура келеді; Әрине, екі, үш және т.б. қарағанда бір параметрді бағалау оңайырақ.
 |
Интегралды экспоненциалды үлестіру функциясын жазу оңай:

Дифференциалдық функцияның көмегімен көрсеткіштік үлестіруді анықтадық; интегралдық функция арқылы анықтауға болатыны анық.
Түсініктеме: Үздіксіз кездейсоқ шаманы қарастырыңыз Т
- бұйымның ақаусыз жұмыс істеу уақытының ұзақтығы. Оның қабылданған мәндері арқылы белгіленеді т
, . Кумулятивтік таралу функциясы ![]() анықтайды сәтсіздік ықтималдығыбелгілі бір уақыт аралығындағы өнімдер т
. Демек, бір уақытта, ұзақтықта ақаусыз жұмыс істеу ықтималдығы т
, яғни қарама-қарсы оқиғаның ықтималдығы тең
анықтайды сәтсіздік ықтималдығыбелгілі бір уақыт аралығындағы өнімдер т
. Демек, бір уақытта, ұзақтықта ақаусыз жұмыс істеу ықтималдығы т
, яғни қарама-қарсы оқиғаның ықтималдығы тең
Қалыпты таралу ( қалыпты таралу) - деректерді талдауда маңызды рөл атқарады.
Кейде терминнің орнына қалыпты таратутерминін қолданыңыз Гаусс таралуК.Гаусс құрметіне (қазіргі уақытта іс жүзінде қолданылмайтын ескі терминдер: Гаусс заңы, Гаусс-Лапластың таралуы).
Бір айнымалы қалыпты таралу
Қалыпты таралудың тығыздығы бар:
Бұл формулада тіркелген параметрлер орташа, - стандартты ауытқу.
Әртүрлі параметрлер үшін тығыздық графиктері берілген.
Қалыпты таралудың сипаттамалық функциясы келесі түрде болады:
![]()
Сипаттама функциясы мен параметрін саралау t = 0, біз кез келген тапсырыстың сәттерін аламыз.
Қалыпты таралу тығыздығы қисығы симметриялы және осы нүктеде бір максимумға тең,
Стандартты ауытқу параметрі 0-ден ∞ аралығында өзгереді.
Орташа -∞ мен +∞ аралығында өзгереді.
Параметр өскен сайын қисық ось бойымен таралады X, 0-ге жақындаған сайын ол орташа мәннің айналасында кішірейеді (параметр таралуды, шашырауды сипаттайды).
Ол өзгерген кезде қисық ось бойымен жылжиды X(графиктерді қараңыз).
Параметрлерді өзгерту және , біз әртүрлі үлгілерді аламыз кездейсоқ айнымалылар, телефонияда пайда болады.
Мысалы, телекоммуникациялық деректерді талдауда қалыпты заңның әдеттегі қолданылуы шу, кедергі, қателер және трафикті сипаттайтын сигналдарды модельдеу болып табылады.
Бір айнымалы қалыпты таралу графиктері

Сурет 1. Қалыпты таралу тығыздық графигі: орташа 0, стандартты ауытқу 1

Сурет 2. Барлық бақылаулардың 68% және 95% құрайтын аймақтармен стандартты қалыпты таралудың тығыздық графигі

Сурет 3. Орташа нөлдік және әртүрлі ауытқулары бар қалыпты таралулардың тығыздық графиктері (=0,5, =1, =2)

4-сурет N(-2,2) және N(3,2) екі қалыпты таралу графиктері.
Параметрді өзгерткен кезде үлестірім орталығы ауысқанына назар аударыңыз.
Түсініктеме
Бағдарламада СТАТИСТИКА N(3,2) белгілеу параметрлері бар қалыпты немесе Гаусс заңын білдіреді: орташа = 3 және стандартты ауытқу =2.
Әдебиетте кейде екінші параметр ретінде түсіндіріледі дисперсия, яғни. шаршыстандартты ауытқу.
Ықтималдық калькуляторы арқылы қалыпты үлестіру пайыздық нүктелерін есептеу СТАТИСТИКА
Ықтималдық калькуляторын қолдану СТАТИСТИКАСіз ескі кітаптарда қолданылған қиын кестелерге жүгінбей-ақ таралулардың әртүрлі сипаттамаларын есептей аласыз.
1-қадам.Іске кірісейік Талдау / Ықтималдық калькуляторы / Бөлулер.
Тарату бөлімінде таңдаңыз қалыпты.

Сурет 5. Ықтималдылықты бөлу калькуляторын іске қосу
2-қадам.Бізді қызықтыратын параметрлерді көрсетеміз.
Мысалы, орташа 0 және стандартты ауытқуы 1 болатын қалыпты үлестірімнің 95% квантилін есептегіміз келеді.
Калькулятордың өрістерінде осы параметрлерді көрсетейік (орташа және стандартты ауытқу калькулятор өрістерін қараңыз).
p=0,95 параметрін енгізейік.
«Кері қайтару» құсбелгісін қойыңыз. автоматты түрде пайда болады. «Кесте» құсбелгісін қойыңыз.
Жоғарғы оң жақ бұрыштағы «Есептеу» түймесін басыңыз.

Сурет 6. Параметрлерді орнату
3-қадам. Z өрісінде біз нәтиже аламыз: квантилдік мән 1,64 (келесі терезені қараңыз).

Сурет 7. Калькулятордың нәтижесін қарау

Сурет 8. Тығыздық графиктері және таралу функциялары. Түзу сызық x=1,644485




Сурет 9. Қалыпты таралу функциясының графиктері. Тік нүктелі сызықтар - x=-1,5, x=-1, x=-0,5, x=0


Сурет 10. Қалыпты таралу функциясының графиктері. Тік нүктелі сызықтар - x=0,5, x=1, x=1,5, x=2
Қалыпты таралу параметрлерін бағалау
Қалыпты таралу мәндерін пайдалану арқылы есептеуге болады интерактивті калькулятор.
Екі айнымалы қалыпты таралу
Бірөлшемді қалыпты таралу табиғи түрде жалпыланады екі өлшемдіқалыпты таралу.
Мысалы, егер сіз сигналды тек бір нүктеде қарастырсаңыз, онда сіз үшін бір өлшемді бөлу жеткілікті, екі нүктеде - екі өлшемді, үш нүктеде - үш өлшемді және т.б.
Екі айнымалы қалыпты таралудың жалпы формуласы:

арасындағы жұптық корреляция қайда X 1Және X 2;
X 1тиісінше;
Айнымалының орташа және стандартты ауытқуы X 2тиісінше.
Кездейсоқ айнымалылар болса X 1Және X 2тәуелсіз болса, онда корреляция сәйкесінше 0, = 0 болады, дәрежедегі ортаңғы мүше жойылады және бізде:
f(x 1 ,x 2) = f(x 1)*f(x 2)
Тәуелсіз шамалар үшін екі өлшемді тығыздық екі бір өлшемді тығыздықтың көбейтіндісіне ыдырайды.
Екі айнымалы қалыпты таралулардың тығыздық графиктері

Сурет 11. Екі айнымалы қалыпты үлестірімнің тығыздық графигі (орталардың нөлдік векторы, бірлік коварианттық матрица)

Сурет 12. z=0,05 жазықтығымен екі өлшемді қалыпты үлестірімнің тығыздық графигінің қимасы.

Сурет 13. Екі өлшемді қалыпты үлестірімнің тығыздық графигі (күтілетін мәннің нөлдік векторы, негізгі диагоналында 1 және бүйір диагоналында 0,5 болатын коварианттық матрица)

14-сурет. Екі өлшемді қалыпты үлестірімнің тығыздық графигінің (математикалық күтудің нөлдік векторы, негізгі диагоналында 1 және бүйір диагоналында 0,5 болатын коварианттық матрица) z= 0,05 жазықтығы бойынша кесіндісі.

Сурет 15. Екі өлшемді қалыпты үлестірімнің тығыздық графигі (күтілетін мәннің нөлдік векторы, негізгі диагоналында 1 және бүйір диагоналында -0,5 болатын коварианттық матрица)

Сурет 16. Екі өлшемді қалыпты үлестірімнің тығыздық графигінің (математикалық күтудің нөлдік векторы, негізгі диагоналында 1 және бүйір диагоналында -0,5 болатын коварианттық матрица) z=0,05 жазықтықтағы қимасы.

Сурет 17. z=0,05 жазықтығымен екі өлшемді қалыпты үлестірімнің тығыздық графиктерінің кесінділері.
Екі айнымалы қалыпты үлестіруді жақсырақ түсіну үшін келесі есепті шешіп көріңіз.
Тапсырма. Екі айнымалы қалыпты таралу графигін қараңыз. Ойлап көріңізші, оны бір өлшемді қалыпты таралу графигінің айналуы ретінде көрсетуге бола ма? Деформация техникасын қашан қолдану керек?
Іс жүзінде кездейсоқ шамалардың көпшілігі әсер етеді көп саныкездейсоқ факторлар қалыпты ықтималдық таралу заңына бағынады. Сондықтан ықтималдықтар теориясының әртүрлі қолданбаларында бұл заң ерекше маңызға ие.
Кездейсоқ шама $X$ қалыпты ықтималдық таралу заңына бағынады, егер оның ықтималдығының таралу тығыздығы келесі түрде болса
$$f\left(x\right)=((1)\over (\sigma \sqrt(2\pi )))e^(-(((\left(x-a\оң))^2)\үстінде 2(\sigma )^2)))$$
$f\left(x\right)$ функциясының графигі суретте схемалық түрде көрсетілген және «Гаусс қисығы» деп аталады. Бұл графиктің оң жағында еуро айналымға енгізілгенге дейін қолданылған неміс 10 маркалы банкнота орналасқан. Мұқият қарасаңыз, бұл банкнотадан Гаусс қисығын және оны ашқан ұлы математик Карл Фридрих Гауссты көре аласыз.
$f\left(x\right)$ тығыздық функциямызға оралайық және $a,\ (\sigma )^2$ таралу параметрлеріне қатысты кейбір түсініктемелер берейік. $a$ параметрі кездейсоқ шама мәндерінің дисперсия центрін сипаттайды, яғни ол математикалық күту мәніне ие. $a$ параметрі өзгерген кезде және $(\sigma )^2$ параметрі өзгеріссіз қалғанда, біз $f\left(x\right)$ функциясының графигінің абсцисса бойымен ығысуын байқауға болады, ал тығыздық графигі өзі пішінін өзгертпейді.

$(\sigma )^2$ параметрі дисперсия болып табылады және $f\left(x\right)$ тығыздық графигі қисығының пішінін сипаттайды. $(\sigma )^2$ параметрін $a$ параметрімен өзгерткен кезде абсцисса осі бойымен қозғалмай-ақ, тығыздық графигі оның пішінін қалай өзгертетінін, қысу немесе созылуды байқауға болады.

Қалыпты таралған кездейсоқ шаманың берілген интервалға түсу ықтималдығы
Белгілі болғандай, $X$ кездейсоқ шамасының $\left(\alpha ;\ \beta \right)$ интервалына түсу ықтималдығын $P\left(\alpha) есептеуге болады.< X < \beta \right)=\int^{\beta }_{\alpha }{f\left(x\right)dx}$. Для нормального распределения случайной величины $X$ с параметрами $a,\ \sigma $ справедлива следующая формула:
$$P\сол(\альфа< X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right)$$
Мұндағы $\Phi \left(x\right)=((1)\over (\sqrt(2\pi )))\int^x_0(e^(-t^2/2)dt)$ функциясы Лаплас функциясы. Бұл функцияның мәндері -ден алынады. $\Phi \left(x\right)$ функциясының келесі қасиеттерін атап өтуге болады.

1 . $\Phi \left(-x\right)=-\Phi \left(x\right)$, яғни $\Phi \left(x\right)$ функциясы тақ.
2 . $\Phi \left(x\right)$ - монотонды өсетін функция.
3 . $(\mathop(lim)_(x\to +\infty ) \Phi \left(x\right)\ )=0,5$, $(\mathop(lim)_(x\to -\infty ) \ Phi \ сол жақ(x\оң)\ )=-0,5$.
$\Phi \left(x\right)$ функциясының мәндерін есептеу үшін Excel бағдарламасындағы $f_x$ шеберін де пайдалануға болады: $\Phi \left(x\right)=NORMDIST\left(x) ;0;1;1\оң жақ )-0,5$. Мысалы, $x=2$ үшін $\Phi \left(x\right)$ функциясының мәндерін есептейік.

$X\in N\left(a;\ (\sigma )^2\right)$ қалыпты таралған кездейсоқ шамасының $a$ математикалық күтуге қатысты симметриялы интервалға түсу ықтималдығын формула арқылы есептеуге болады.
$$P\left(\left|X-a\right|< \delta \right)=2\Phi \left({{\delta }\over {\sigma }}\right).$$
Үш сигма ережесі. Қалыпты таралған кездейсоқ шама $X$ $\left(a-3\sigma ;a+3\sigma \right)$ интервалына түсетіні анық.
1-мысал . $X$ кездейсоқ шама $a=2,\ \sigma =3$ параметрлері бар қалыпты ықтималдық таралу заңына бағынады. $X$ $\left(0.5;1\right)$ интервалына түсу ықтималдығын және $\left|X-a\right| теңсіздігін қанағаттандыру ықтималдығын табыңыз.< 0,2$.
Формула қолдану
$$P\сол(\альфа< X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right),$$
$P\left(0,5;1\right)=\Phi \left(((1-2)\over(3))\right)-\Phi \left(((0,5-2)\(3) үстінде табамыз. ))\оң)=\Phi \left(-0,33\оң)-\Phi \left(-0,5\right)=\Phi \left(0,5\оң)-\Phi \ left(0,33\оң)=0,191- 0,129=0,062 доллар.
$$P\left(\left|X-a\right|< 0,2\right)=2\Phi \left({{\delta }\over {\sigma }}\right)=2\Phi \left({{0,2}\over {3}}\right)=2\Phi \left(0,07\right)=2\cdot 0,028=0,056.$$
2-мысал . Бір жыл ішінде белгілі бір компанияның акцияларының бағасы 50 шартты ақша бірлігіне тең математикалық күтумен және 10-ға тең стандартты ауытқумен қалыпты заң бойынша бөлінген кездейсоқ шама болсын делік. Кездейсоқ таңдалған акцияның ықтималдығы қандай талқыланатын кезеңнің күні науқанның бағасы:
а) 70-тен астам шартты ақша бірлігі?
б) акцияға 50-ден төмен ме?
в) акцияға 45 пен 58 шартты ақша бірлігі арасында?
Кездейсоқ шама $X$ қандай да бір компанияның акцияларының бағасы болсын. Шарт бойынша $X$ $a=50$ - математикалық күту, $\сигма =10$ - стандартты ауытқу параметрлері бар қалыпты үлестірімге бағынады. Ықтималдық $P\left(\альфа< X < \beta \right)$ попадания $X$ в интервал $\left(\alpha ,\ \beta \right)$ будем находить по формуле:
$$P\сол(\альфа< X < \beta \right)=\Phi \left({{\beta -a}\over {\sigma }}\right)-\Phi \left({{\alpha -a}\over {\sigma }}\right).$$
$$а)\ P\left(X>70\оң)=\Phi \left(((\infty -50)\(10))\оң жақта)-\Phi \left(((70-50)\ жоғары (10))\оң)=0,5-\Phi \сол(2\оң)=0,5-0,4772=0,0228.$$
$$b)\P\сол(X< 50\right)=\Phi \left({{50-50}\over {10}}\right)-\Phi \left({{-\infty -50}\over {10}}\right)=\Phi \left(0\right)+0,5=0+0,5=0,5.$$
$$in)\ P\left(45< X < 58\right)=\Phi \left({{58-50}\over {10}}\right)-\Phi \left({{45-50}\over {10}}\right)=\Phi \left(0,8\right)-\Phi \left(-0,5\right)=\Phi \left(0,8\right)+\Phi \left(0,5\right)=$$
Қалыпты ықтималдықтардың таралу заңы
Оны әсірелеусіз философиялық заңдылық деп атауға болады. Бізді қоршаған дүниедегі әртүрлі нысандар мен процестерді бақылай отырып, біз жиі бірдеңе жеткіліксіз екенін және норма бар екеніне тап боламыз: 
Міне, негізгі көрініс тығыздық функцияларықалыпты ықтималдық үлестірімі және мен сізді осы қызықты сабаққа қош келдіңіз.
Қандай мысалдар келтіре аласыз? Олардың жай ғана қараңғылығы бар. Бұл, мысалы, адамдардың бойы, салмағы (тек қана емес), олардың физикалық күші, ақыл-ой қабілеттері және т.б. «Негізгі масса» бар (бір себептермен немесе басқа)және екі бағытта да ауытқулар бар.
Бұл жансыз заттардың әртүрлі сипаттамалары (бірдей өлшем, салмақ). Бұл процестердің кездейсоқ ұзақтығы, мысалы, жүз метрлік жарыс уақыты немесе шайырдың кәріптасқа айналуы. Физикадан мен ауа молекулаларын есіме түсірдім: олардың кейбіреулері баяу, кейбіреулері жылдам, бірақ көпшілігі «стандартты» жылдамдықпен қозғалады.
Содан кейін біз орталықтан тағы бір стандартты ауытқуға ауытқып, биіктікті есептейміз: 
Сызбадағы нүктелерді белгілеу (жасыл түс)және бұл жеткілікті екенін көріп отырмыз.
Соңғы кезеңде біз графикті мұқият сызамыз және әсіресе мұқиятоны бейнелеңіз дөңес/ойыс! Сіз x осі екенін әлдеқашан түсінген шығарсыз көлденең асимптота, және оның артына «көтерілуге» мүлдем тыйым салынады!
Шешімді электронды түрде тапсырған кезде Excel бағдарламасында график құру оңай, мен күтпеген жерден мен тіпті осы тақырып бойынша қысқа бейне түсірдім. Бірақ алдымен қалыпты қисық пішіні және мәндеріне байланысты қалай өзгеретіні туралы сөйлесейік.
«a» көбейту немесе азайту кезінде (тұрақты «сигмамен»)график өзінің пішінін сақтайды және оңға/солға жылжидытиісінше. Мысалы, функция пішінді қабылдағанда ![]() және біздің график 3 бірлік солға – дәл координаталар басына «жылжытады»:
және біздің график 3 бірлік солға – дәл координаталар басына «жылжытады»: 
Нөлдік математикалық күтумен қалыпты бөлінген шама толығымен табиғи атау алды - орталықтандырылған; оның тығыздық функциясы тіпті, ал график ординатаға қатысты симметриялы.
«Сигма» өзгерген жағдайда («а» тұрақтысымен), график «бірдей қалады», бірақ пішінін өзгертеді. Ұлғайған кезде ол сегізаяқтың шандырларын созып тұрғандай төменірек және ұзартылған болады. Және, керісінше, графикті азайтқанда тар және биік болады- бұл «таң қалған сегізаяқ» болып шығады. Иә, қашан төмендеуі«сигма» екі рет: алдыңғы график екі рет тарылып, ұзарады: 
Барлығы толығымен сәйкес келеді графиктердің геометриялық түрлендірулері.
Бірлік сигма мәні бар қалыпты үлестірім деп аталады нормаланған, және егер ол да болса орталықтандырылған(біздің жағдайымыз), онда мұндай бөлу шақырылады стандартты. Ол одан да көп қарапайым функциябұрын кездескен тығыздық Лапластың жергілікті теоремасы: ![]() . Стандартты дистрибуция тәжірибеде кең қолданыс тапты және жақын арада біз оның мақсатын түсінеміз.
. Стандартты дистрибуция тәжірибеде кең қолданыс тапты және жақын арада біз оның мақсатын түсінеміз.
Ал енді фильмді көрейік:
Иә, мүлдем дұрыс - әйтеуір ол көлеңкеде қалды ықтималдықты бөлу функциясы. Оны еске алайық анықтамасы:
– кездейсоқ шаманың барлық нақты мәндерден «плюс» шексіздікке дейін «өтетін» айнымалыдан КІШІ мән қабылдау ықтималдығы.
Интегралдың ішінде әдетте басқа әріп қолданылады, сондықтан белгілермен «қабаттасулар» болмайды, өйткені мұнда әрбір мән байланыстырылады. дұрыс емес интеграл, бұл кейбіреулеріне тең саныаралықтан.
Барлық дерлік мәндерді дәл есептеу мүмкін емес, бірақ біз жаңа көргеніміздей, қазіргі заманғы есептеуіш қуатпен бұл қиын емес. Осылайша, стандартты тарату функциясы үшін сәйкес Excel функциясы әдетте бір аргументті қамтиды:
=NORMSDIST(z)
Бір, екі - және сіз аяқтадыңыз: 
Сызбада барлығының орындалуы анық көрсетілген бөлу функциясының қасиеттері, және мұнда техникалық нюанстарға назар аудару керек көлденең асимптоталаржәне иілу нүктесі.
Енді тақырыптың негізгі тапсырмаларының бірін еске түсірейік, атап айтқанда, қалыпты кездейсоқ шаманың ықтималдығын қалай табуға болатынын білейік. мәнді интервалдан алады. Геометриялық тұрғыдан бұл ықтималдық тең аумақСәйкес бөлімдегі қалыпты қисық пен x осі арасындағы: 
бірақ мен шамамен мән алуға тырысамын  негізсіз, сондықтан оны пайдалану ұтымдырақ «жеңіл» формула:
негізсіз, сондықтан оны пайдалану ұтымдырақ «жеңіл» формула:
.
! Сондай-ақ еске түсіреді , Не
Мұнда сіз Excel бағдарламасын қайтадан пайдалана аласыз, бірақ бірнеше маңызды «бірақ» бар: біріншіден, ол әрқашан қолында емес, екіншіден, «дайын» мәндер мұғалімнің сұрақтарын тудыруы мүмкін. Неліктен?
Мен бұл туралы бұрын бірнеше рет айтқанмын: бір кездері (және жақын арада) кәдімгі калькулятор сән-салтанат болды, ал оқу әдебиетіҚарастырылып отырған мәселені шешудің «қолмен» әдісі әлі күнге дейін сақталған. Оның мәні мынада стандарттау«альфа» және «бета» мәндері, яғни шешімді стандартты таратуға дейін азайтады: ![]()
Ескерту
: функцияны жалпы жағдайдан алу оңай сызықтық қолдану ауыстырулар. Сонымен қатар:
сызықтық қолдану ауыстырулар. Сонымен қатар:
және орындалған ауыстырудан ерікті таралу мәндерінен стандартты үлестірімнің сәйкес мәндеріне көшу формуласы дәл келеді.
Бұл не үшін қажет? Өйткені, құндылықтарды ата-бабаларымыз мұқият есептеп, тервердегі көптеген кітаптарда бар арнайы кестеге жинаған. Бірақ біз қазірдің өзінде қарастырған құндылықтар кестесі жиі кездеседі Лапластың интегралдық теоремасы:
Егер біздің қолымызда Лаплас функциясының мәндер кестесі болса  , содан кейін біз оны шешеміз:
, содан кейін біз оны шешеміз:
Бөлшек мәндер әдеттегі кестеде көрсетілгендей, 4 ондық таңбаға дейін дөңгелектенеді. Ал бақылау үшін бар 5-тармақ макет.
Мен бұл туралы еске саламын және шатастырмау үшін әрқашан бақылау, сіздің көз алдыңызда НЕ функциясының кестесі.
Жауаппайызбен берілуі қажет, сондықтан есептелген ықтималдық 100-ге көбейтіліп, нәтиже мағыналы түсініктемемен қамтамасыз етілуі керек:
– 5-тен 70 м-ге дейін ұшу кезінде снарядтардың шамамен 15,87% түседі.
Біз өз бетімізше жаттығамыз:
3-мысал
Зауытта жасалған мойынтіректердің диаметрі кездейсоқ шама, математикалық болжамы 1,5 см және стандартты ауытқуы 0,04 см қалыпты үлестіріледі.Кездейсоқ таңдалған подшипниктің өлшемі 1,4-тен 1,6 см-ге дейін болуы ықтималдығын табыңыз.
Үлгі шешімде және төменде мен Лаплас функциясын ең көп таралған опция ретінде қолданамын. Айтпақшы, тұжырымға сәйкес интервалдың ұштарын мұнда қарастыруға қосуға болатынын ескеріңіз. Дегенмен, бұл сыни емес.
Бұл мысалда біз ерекше жағдайды кездестірдік - интервал математикалық күтуге қатысты симметриялы болғанда. Мұндай жағдайда оны келесі түрде жазуға болады және Лаплас функциясының тақтығын пайдаланып, жұмыс формуласын жеңілдетеді:

Delta параметрі шақырылады ауытқуматематикалық күтуден және қосарланған теңсіздікті «орауға» болады модуль:
– кездейсоқ шама мәнінің математикалық күтуден кем ауытқу ықтималдығы.
Шешім бір жолға сәйкес келетіні жақсы :)
– кездейсоқ алынған мойынтіректің диаметрі 1,5 см-ден 0,1 см-ден аспайтындай ықтималдығы.
Бұл тапсырманың нәтижесі бірлікке жақын болды, бірақ мен одан да жоғары сенімділікті қалаймын - дәлірек айтқанда, диаметрі орналасқан шекараларды анықтау барлығы дерлікподшипниктер. Бұл үшін қандай да бір критерий бар ма? Бар! Қойылған сұраққа деп аталатын жауап береді
үш сигма ережесі
Оның мәні мынада іс жүзінде сенімді
қалыпты үлестірілген кездейсоқ шама интервалдан мән алатын факті болып табылады ![]() .
.
Шынында да, күтілетін мәннен ауытқу ықтималдығы мынадан аз:
немесе 99,73%
Мойынтіректерге келетін болсақ, бұл диаметрі 1,38-ден 1,62 см-ге дейінгі 9973 дана және тек 27 «стандартты емес» көшірмелер.
IN практикалық зерттеулерҮш сигма ережесі әдетте қарама-қарсы бағытта қолданылады: егер статистикалықБарлық дерлік құндылықтар екені анықталды зерттелетін кездейсоқ шама 6 стандартты ауытқу интервалына түссе, онда бұл мән қалыпты заңға сәйкес таратылады деп есептейтін сенімді себептер бар. Тексеру теорияның көмегімен жүзеге асырылады статистикалық гипотезалар.
Біз кеңестік қиын мәселелерді шешуді жалғастырамыз:
4-мысал
Өлшеу қателігінің кездейсоқ мәні нөлдік математикалық күтумен және 3 грамм стандартты ауытқумен қалыпты заң бойынша бөлінеді. Абсолюттік мәнде 5 грамнан аспайтын қателікпен келесі таразылаудың орындалу ықтималдығын табыңыз.
Шешімөте қарапайым. Шарт бойынша біз келесі таразыда бірден байқаймыз (бірдеңе немесе біреу)біз 9 грамм дәлдікпен нәтижені 100% дерлік аламыз. Бірақ мәселе неғұрлым тар ауытқуды қамтиды және формулаға сәйкес:
![]() – келесі салмақ өлшеудің 5 граммнан аспайтын қателікпен орындалу ықтималдығы.
– келесі салмақ өлшеудің 5 граммнан аспайтын қателікпен орындалу ықтималдығы.
Жауап:
Шешілген мәселе ұқсас болып көрінетін мәселеден түбегейлі ерекшеленеді. 3-мысалтуралы сабақ біркелкі бөлу. Қате болды дөңгелектеуөлшеу нәтижелері, мұнда біз өлшеулердің кездейсоқ қателігі туралы айтып отырмыз. Мұндай қателер құрылғының өзінің техникалық сипаттамаларына байланысты туындайды. (жол берілетін қателер ауқымы әдетте оның төлқұжатында көрсетіледі), сонымен қатар экспериментатордың кінәсінен - біз, мысалы, «көзбен» бірдей таразының инесінен көрсеткіштерді алған кезде.
Басқалардың арасында деп аталатындар да бар жүйеліөлшеу қателері. Қазірдің өзінде кездейсоқ емесқұрылғының дұрыс орнатылмауына немесе жұмыс істеуіне байланысты туындайтын қателер. Мысалы, реттелмейтін еден таразылары килограммдарды тұрақты түрде «қосу» мүмкін, ал сатушы тұтынушыларды жүйелі түрде салмақтайды. Немесе оны жүйелі емес есептеуге болады. Дегенмен, кез келген жағдайда мұндай қате кездейсоқ болмайды және оның күтуі нөлден ерекшеленеді.
…Мен шұғыл түрде сату бойынша оқыту курсын әзірлеп жатырмын =)
Кері есепті өзіміз шешейік:
5-мысал
Роликтің диаметрі кездейсоқ қалыпты таралған кездейсоқ шама, оның стандартты ауытқуы мм-ге тең. Математикалық күтуге қатысты симметриялы аралық ұзындығын табыңыз, оған ролик диаметрінің ұзындығы түсуі мүмкін.
5-нүкте* дизайн макетикөмекке. Бұл жерде математикалық күту белгісіз екенін ескеріңіз, бірақ бұл мәселені шешуге кедергі жасамайды.
ЖӘНЕ емтихан тапсырмасы, мен оны материалды біріктіру үшін өте ұсынамын:
6-мысал
Қалыпты таралған кездейсоқ шама оның параметрлері (математикалық күту) және (стандартты ауытқу) арқылы көрсетіледі. Міндетті:
а) ықтималдық тығыздығын жазып, оның графигін схемалық түрде бейнелеу;
б) интервалдан мән алу ықтималдығын табыңыз ![]() ;
;
в) абсолютті шаманың -нен артық емес ауытқу ықтималдығын табыңыз;
г) «үш сигма» ережесін пайдаланып, кездейсоқ шаманың мәндерін табыңыз.
Мұндай мәселелер барлық жерде ұсынылады, мен көптеген жылдар бойы тәжірибе жүзінде олардың жүздегенін және жүздегенін шештім. Міндетті түрде қолмен сурет салуды және қағаз кестелерді пайдалануды үйреніңіз;)
Ал, мен күрделіліктің жоғарылау мысалын қарастырамын:
7-мысал
Кездейсоқ шаманың ықтималдылық таралу тығыздығы пішінге ие ![]() . Табу, математикалық күту, дисперсия, үлестіру функциясы, тығыздық графиктері мен таралу функцияларын құру, табу.
. Табу, математикалық күту, дисперсия, үлестіру функциясы, тығыздық графиктері мен таралу функцияларын құру, табу.
Шешім: Ең алдымен, шарт кездейсоқ шаманың табиғаты туралы ештеңе айтпайтынын атап өтейік. Көрсеткіштің болуы өздігінен ештеңені білдірмейді: ол, мысалы, болуы мүмкін индикативтінемесе тіпті ерікті үздіксіз тарату. Сондықтан бөлудің «қалыптылығын» әлі де негіздеу керек:
Функциядан бері ![]() бойынша анықталады кез келгеннақты мән , және оны түрге келтіруге болады, содан кейін кездейсоқ шама қалыпты заңға сәйкес таратылады.
бойынша анықталады кез келгеннақты мән , және оны түрге келтіруге болады, содан кейін кездейсоқ шама қалыпты заңға сәйкес таратылады.
Мінеки біз. Осыған толық шаршыны таңдаңызжәне ұйымдастыру үш қабатты бөлшек:
Көрсеткішті бастапқы пішініне қайтара отырып, тексеруді орындаңыз:
, бұл біз көргіміз келген.
Осылайша:  - бойынша өкілеттіктері бар операциялар ережесі«шымшу» Мұнда сіз бірден анық сандық сипаттамаларды жаза аласыз:
- бойынша өкілеттіктері бар операциялар ережесі«шымшу» Мұнда сіз бірден анық сандық сипаттамаларды жаза аласыз:
Енді параметрдің мәнін табайық. Қалыпты таралу көбейткіші және пішініне ие болғандықтан, онда:  , бұл жерден біз функциямызды білдіреміз және ауыстырамыз:
, бұл жерден біз функциямызды білдіреміз және ауыстырамыз:  , содан кейін біз жазбаны тағы да өз көзімізбен қарап шығамыз және алынған функцияның пішіні бар екеніне көз жеткіземіз
, содан кейін біз жазбаны тағы да өз көзімізбен қарап шығамыз және алынған функцияның пішіні бар екеніне көз жеткіземіз  .
.
Тығыздық графигін құрайық: 
және таралу функциясының графигі  :
:
Егер сізде Excel бағдарламасы немесе тіпті қарапайым калькулятор болмаса, соңғы графикті қолмен оңай жасауға болады! Бір нүктеде үлестірім функциясы мән қабылдайды және осы жерден табылады
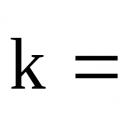 Реакция жылдамдығының тұрақтысы Зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар
Реакция жылдамдығының тұрақтысы Зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар Өлгеннен кейін өмір бар ма?
Өлгеннен кейін өмір бар ма? Ғалымдар: Жер – адамзат ғалымдары үшін «ғарыштық түрме»: Жер – ғаламдағы ғарыш түрмесі
Ғалымдар: Жер – адамзат ғалымдары үшін «ғарыштық түрме»: Жер – ғаламдағы ғарыш түрмесі