Сызықтық теңдеу дегеніміз не. Сызықтық теңдеулер жүйесіне мысалдар: шешу әдісі
Сызықтық теңдеулер жүйесі — әрқайсысында k айнымалысы бар n сызықтық теңдеулердің бірігуі. Ол былай жазылған:
Көптеген адамдар жоғары алгебрамен алғаш рет кездескенде, теңдеулер саны міндетті түрде айнымалылар санымен сәйкес келуі керек деп қателеседі. Мектеп алгебрасында бұл әдетте орын алады, бірақ жоғары алгебра үшін бұл әдетте дұрыс емес.
Теңдеулер жүйесінің шешімі - бұл жүйенің әрбір теңдеуінің шешімі болып табылатын сандар тізбегі (k 1, k 2, ..., k n), яғни. осы теңдеуге x 1, x 2, ..., x n айнымалыларының орнына қойғанда дұрыс сандық теңдікті береді.
Осыған сәйкес теңдеулер жүйесін шешу оның барлық шешімдерінің жиынын табу немесе бұл жиынның бос екенін дәлелдеу дегенді білдіреді. Теңдеулер саны мен белгісіздердің саны сәйкес келмеуі мүмкін болғандықтан, үш жағдай болуы мүмкін:
- Жүйе сәйкес емес, яғни. барлық шешімдер жиынтығы бос. Жүйені шешу үшін қандай әдіс қолданылса да оңай анықталатын өте сирек жағдай.
- Жүйе дәйекті және анықталған, яғни. дәл бір шешімі бар. Мектептен бері белгілі классикалық нұсқасы.
- Жүйе дәйекті және анықталмаған, яғни. шексіз көп шешімдері бар. Бұл ең қиын нұсқа. «Жүйеде шешімдердің шексіз жиынтығы бар» деп көрсету жеткіліксіз - бұл жиынтық қалай құрылымдалғанын сипаттау қажет.
x i айнымалысы рұқсат етілген деп аталады, егер ол жүйенің тек бір теңдеуіне қосылса және коэффициенті 1. Басқаша айтқанда, басқа теңдеулерде x i айнымалысының коэффициенті нөлге тең болуы керек.
Әрбір теңдеуде бір рұқсат етілген айнымалыны таңдасақ, барлық теңдеулер жүйесі үшін рұқсат етілген айнымалылар жиынын аламыз. Бұл пішінде жазылған жүйенің өзі де шешілген деп аталады. Жалпы алғанда, бір және бір түпнұсқа жүйені әртүрлі рұқсат етілгенге дейін азайтуға болады, бірақ әзірге бұл бізді алаңдатпайды. Мұнда рұқсат етілген жүйелердің мысалдары берілген:

Екі жүйе де x 1 , x 3 және x 4 айнымалыларына қатысты шешіледі. Дегенмен, дәл осындай жетістікпен екінші жүйе x 1, x 3 және x 5-ке қатысты шешілген деп айтуға болады. Ең соңғы теңдеуді x 5 = x 4 түрінде қайта жазу жеткілікті.
Енді жалпы жағдайды қарастырайық. Барлығында k айнымалы болсын, олардың ішінде r рұқсат етілген. Сонда екі жағдай болуы мүмкін:
- Рұқсат етілген айнымалылар саны k айнымалылардың жалпы санына тең r: r = k. r = k рұқсат етілген айнымалылар болатын k теңдеулер жүйесін аламыз. Мұндай жүйе бірлескен және белгілі, өйткені x 1 = b 1, x 2 = b 2, ..., x k = b k;
- Рұқсат етілген айнымалылар саны r аз жалпы саныайнымалылар k : r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Сонымен, жоғарыда аталған жүйелерде x 2, x 5, x 6 (бірінші жүйе үшін) және x 2, x 5 (екінші үшін) айнымалылар бос. Бос айнымалылар болған жағдай теорема ретінде жақсы тұжырымдалған:
Назар аударыңыз: бұл өте маңызды нүкте! Нәтижелік жүйені қалай жазуыңызға байланысты бірдей айнымалы рұқсат етілген немесе бос болуы мүмкін. Көптеген жоғары математика мұғалімдері айнымалы мәндерді лексикографиялық тәртіпте жазуды ұсынады, яғни. өсу индексі. Дегенмен, сіз бұл кеңесті орындауға міндетті емессіз.
Теорема. Егер n теңдеулер жүйесінде x 1, x 2, ..., x r айнымалыларына рұқсат етілсе, ал x r + 1, x r + 2, ..., x k бос болса, онда:
- Егер бос айнымалылардың мәндерін орнатсақ (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k), содан кейін x 1, x 2 мәндерін табамыз, ..., x r, біз шешімдердің бірін аламыз.
- Егер екі шешімде бос айнымалылардың мәндері сәйкес келсе, рұқсат етілген айнымалылардың мәндері де сәйкес келеді, яғни. шешімдері тең.
Бұл теореманың мәні неде? Шешілген теңдеулер жүйесінің барлық шешімдерін алу үшін бос айнымалыларды оқшаулау жеткілікті. Содан кейін бос айнымалыларға әртүрлі мәндерді тағайындай отырып, біз аламыз дайын шешімдер. Мұның бәрі - осылайша жүйенің барлық шешімдерін алуға болады. Басқа шешімдер жоқ.
Қорытынды: шешілген теңдеулер жүйесі әрқашан сәйкес келеді. Шешілген жүйедегі теңдеулер саны айнымалылар санына тең болса, жүйе анықталған, аз болса, ол белгісіз болады.
Және бәрі жақсы болар еді, бірақ сұрақ туындайды: бастапқы теңдеулер жүйесінен шешілгенін қалай алуға болады? Бұл үшін бар
т.б., басқа түрдегі теңдеулермен танысу қисынды. Келесі кезекте сызықтық теңдеулер, оны мақсатты түрде оқыту 7-сыныпта алгебра сабақтарында басталады.
Алдымен сызықтық теңдеудің не екенін түсіндіру, сызықтық теңдеуге анықтама беру, оның коэффициенттерін көрсету, көрсету керек екені түсінікті. жалпы формасы. Содан кейін коэффициенттердің мәндеріне және түбірлері қалай табылғанына байланысты сызықтық теңдеудің қанша шешімі бар екенін анықтауға болады. Бұл мысалдарды шешуге көшуге және сол арқылы үйренген теорияны бекітуге мүмкіндік береді. Бұл мақалада біз мұны істейміз: сызықтық теңдеулер мен олардың шешімдеріне қатысты барлық теориялық және практикалық мәселелерге егжей-тегжейлі тоқталамыз.
Бірден айталық, мұнда біз бір айнымалысы бар сызықтық теңдеулерді ғана қарастырамыз, ал жеке мақалада шешу принциптерін зерттейміз. екі айнымалысы бар сызықтық теңдеулер.
Бетті шарлау.
Сызықтық теңдеу дегеніміз не?
Сызықтық теңдеудің анықтамасы оның жазылу тәсілімен беріледі. Оның үстіне әртүрлі математика және алгебра оқулықтарында сызықтық теңдеулердің анықтамаларының тұжырымдары мәселенің мәніне әсер етпейтін кейбір айырмашылықтарға ие.
Мысалы, Ю.Н.Макарычев және т.б.-ның 7-сыныпқа арналған алгебра оқулығында сызықтық теңдеу келесідей анықталады:
Анықтама.
Пішіннің теңдеуі a x=b, мұндағы х айнымалы, a және b кейбір сандар деп аталады бір айнымалысы бар сызықтық теңдеу.
Берілген анықтамаға сәйкес келетін сызықтық теңдеулерге мысалдар келтірейік. Мысалы, 5 х = 10 – бір х айнымалысы бар сызықтық теңдеу, мұндағы а коэффициенті 5, b саны 10. Басқа мысал: −2,3·y=0 да сызықтық теңдеу, бірақ y айнымалысы бар, онда a=−2,3 және b=0. Ал сызықтық теңдеулерде x=−2 және −x=3,33 a анық жоқ және сәйкесінше 1 және −1-ге тең, ал бірінші теңдеуде b=−2, ал екіншісінде b=3,33.
Ал осыдан бір жыл бұрын Н.Я.Виленкиннің математика оқулығында бір белгісізі бар сызықтық теңдеулер, а х = b түріндегі теңдеулерден басқа, бір бөліктен мүшелерді тасымалдау арқылы осы пішінге келтіруге болатын теңдеулер де қарастырылған. теңдеудің қарама-қарсы таңбалы екіншісіне, сондай-ақ ұқсас мүшелерін азайту арқылы. Бұл анықтамаға сәйкес 5 х = 2 х + 6 түріндегі теңдеулер, т.б. сонымен қатар сызықтық.
Өз кезегінде А.Г.Мордковичтің 7-сыныпқа арналған алгебра оқулығында мынадай анықтама берілген:
Анықтама.
Бір x айнымалысы бар сызықтық теңдеу a·x+b=0 түріндегі теңдеу, мұндағы a және b сызықтық теңдеудің коэффициенттері деп аталатын кейбір сандар.
Мысалы, бұл түрдегі сызықтық теңдеулер 2 x−12=0, мұндағы а коэффициенті 2, ал b −12-ге тең, ал a=0,2 және b =4,6 коэффициенттерімен 0,2 y+4,6=0. Бірақ сонымен бірге, a·x+b=0 емес, a·x=b, мысалы, 3·x=12 түріндегі сызықтық теңдеулердің мысалдары бар.
Келешекте алшақтық болмас үшін, бір х айнымалысы және a және b коэффициенттері бар сызықтық теңдеу арқылы a x + b = 0 түріндегі теңдеуді айтамыз. Сызықтық теңдеулердің бұл түрі ең негізделген болып көрінеді, өйткені сызықтық теңдеулер алгебралық теңдеулербірінші дәрежелі. Жоғарыда көрсетілген барлық басқа теңдеулерді, сондай-ақ эквивалентті түрлендірулерді қолдана отырып, a x + b = 0 түріне келтірілетін теңдеулерді біз шақырамыз. сызықтық теңдеулерге келтіретін теңдеулер. Бұл тәсілмен 2 x+6=0 теңдеуі сызықтық теңдеу, ал 2 x=−6, 4+25 y=6+24 y, 4 (x+5)=12, т.б. - Бұл сызықтыққа келтірілетін теңдеулер.
Сызықтық теңдеулерді қалай шешуге болады?
Енді a·x+b=0 сызықтық теңдеулері қалай шешілетінін анықтайтын кез келді. Басқаша айтқанда, сызықтық теңдеудің түбірі бар ма, бар болса, олардың қаншасы және оларды қалай табуға болатынын анықтаудың уақыты келді.
Сызықтық теңдеудің түбірлерінің болуы a және b коэффициенттерінің мәндеріне байланысты. Бұл жағдайда а x+b=0 сызықтық теңдеуі бар
- a≠0 үшін жалғыз түбір,
- a=0 және b≠0 үшін түбірлері жоқ,
- a=0 және b=0 үшін шексіз көп түбірлері бар, бұл жағдайда кез келген сан сызықтық теңдеудің түбірі болады.
Бұл нәтижелердің қалай алынғанын түсіндірейік.
Теңдеулерді шешу үшін бастапқы теңдеуден эквивалентті теңдеулерге, яғни түбірлері бірдей немесе бастапқы теңдеу сияқты түбірлері жоқ теңдеулерге көшуге болатынын білеміз. Ол үшін келесі эквивалентті түрлендірулерді қолдануға болады:
- теңдеудің бір жағынан екінші жағына қарама-қарсы таңбалы мүшені ауыстыру,
- сондай-ақ теңдеудің екі жағын бірдей нөлдік емес санға көбейту немесе бөлу.
Сонымен, a·x+b=0 түріндегі бір айнымалысы бар сызықтық теңдеуде b мүшесін сол жақтан оң жаққа қарама-қарсы таңбамен жылжытуға болады. Бұл жағдайда теңдеу a·x=−b түрінде болады.
Содан кейін теңдеудің екі жағын а санына бөлу туралы сұрақ туындайды. Бірақ бір нәрсе бар: а саны нөлге тең болуы мүмкін, бұл жағдайда мұндай бөлу мүмкін емес. Бұл мәселені шешу үшін алдымен а саны нөл емес деп есептейміз, ал нөлге тең болу жағдайын сәл кейінірек бөлек қарастырамыз.
Сонымен, егер а нөлге тең болмаса, онда a·x=−b теңдеуінің екі жағын а-ға бөлуге болады, содан кейін ол x=(−b):a түріне түрленеді, бұл нәтиже болуы мүмкін. сияқты бөлшектік қиғаш сызық арқылы жазылады.
Сонымен, a≠0 үшін a·x+b=0 сызықтық теңдеуі оның түбірі көрінетін теңдеуге эквивалентті.
Бұл түбір бірегей, яғни сызықтық теңдеудің басқа түбірі жоқ екенін көрсету оңай. Бұл сізге қарсы әдісті орындауға мүмкіндік береді.
Түбірді x 1 деп белгілейік. Біз x 2 деп белгілейтін сызықтық теңдеудің тағы бір түбірі бар деп алайық, және x 2 ≠x 1, ол мынаған байланысты айырымы арқылы тең сандарды анықтау x 1 −x 2 ≠0 шартына эквивалент. x 1 және x 2 a·x+b=0 сызықтық теңдеуінің түбірлері болғандықтан, a·x 1 +b=0 және a·x 2 +b=0 сандық теңдіктері орындалады. Бұл теңдіктердің сәйкес бөліктерін алып тастай аламыз, бұл сандық теңдіктердің қасиеттері бізге мүмкіндік береді, бізде a·x 1 +b−(a·x 2 +b)=0−0, одан a·(x 1) −x 2)+( b−b)=0, содан кейін a·(x 1 −x 2)=0 . Бірақ бұл теңдік мүмкін емес, өйткені a≠0 және x 1 − x 2 ≠0. Сонымен a≠0 үшін a·x+b=0 сызықтық теңдеуінің түбірінің бірегейлігін дәлелдейтін қайшылыққа келдік.
Сонымен a≠0 үшін a·x+b=0 сызықтық теңдеуін шештік. Осы тармақтың басында келтірілген бірінші нәтиже негізделген. a=0 шартын қанағаттандыратын тағы екі қалды.
a=0 болғанда, a·x+b=0 сызықтық теңдеуі 0·x+b=0 түрін алады. Осы теңдеуден және сандарды нөлге көбейту қасиетінен шығатыны, қандай санды х деп алсақ та, оны 0 x + b=0 теңдеуіне ауыстырғанда b=0 сандық теңдігі шығады. Бұл теңдік b=0 болғанда дұрыс, ал басқа жағдайларда b≠0 болғанда бұл теңдік жалған болады.
Демек, a=0 және b=0 кезінде кез келген сан a·x+b=0 сызықтық теңдеуінің түбірі болады, өйткені бұл шарттарда х орнына кез келген санды қою 0=0 дұрыс сандық теңдікті береді. Ал a=0 және b≠0 болғанда, a·x+b=0 сызықтық теңдеуінің түбірі болмайды, өйткені бұл шарттарда х орнына кез келген санды қою дұрыс емес b=0 сандық теңдігіне әкеледі.
Келтірілген негіздемелер кез келген сызықтық теңдеуді шешуге мүмкіндік беретін әрекеттер тізбегін тұжырымдауға мүмкіндік береді. Сонымен, сызықтық теңдеуді шешу алгоритмібұл:
- Біріншіден, сызықтық теңдеуді жазу арқылы a және b коэффициенттерінің мәндерін табамыз.
- Егер a=0 және b=0 болса, онда бұл теңдеудің шексіз көп түбірі болады, атап айтқанда, кез келген сан осы сызықтық теңдеудің түбірі болады.
- Егер а нөлге тең болса, онда
- b коэффициенті қарама-қарсы таңбамен оң жаққа ауыстырылады, ал сызықтық теңдеу a·x=−b түріне түрленеді,
- содан кейін алынған теңдеудің екі жағы да нөлдік емес а санына бөлінеді, бұл бастапқы сызықтық теңдеудің қажетті түбірін береді.
Жазбаша алгоритм сызықтық теңдеулерді шешу жолы туралы сұраққа жан-жақты жауап береді.
Осы тармақты қорытындылай келе, a·x=b түріндегі теңдеулерді шешу үшін осыған ұқсас алгоритм қолданылатынын айта кеткен жөн. Оның айырмашылығы мынада: a≠0 кезінде теңдеудің екі жағы да бірден осы санға бөлінеді; мұнда b теңдеудің қажетті бөлігінде болды және оны тасымалдаудың қажеті жоқ.
a x = b түріндегі теңдеулерді шешу үшін келесі алгоритм қолданылады:
- Егер a=0 және b=0 болса, онда теңдеудің шексіз көп түбірі болады, олар кез келген сандар.
- Егер a=0 және b≠0 болса, онда бастапқы теңдеудің түбірі болмайды.
- Егер а нөл емес болса, онда теңдеудің екі жағы да нөлдік емес а санына бөлінеді, одан теңдеудің жалғыз түбірі табылады, b/a-ға тең.
Сызықтық теңдеулерді шешу мысалдары
Жаттығуға көшейік. Сызықтық теңдеулерді шешу алгоритмі қалай қолданылатынын қарастырайық. Сызықтық теңдеулердің коэффициенттерінің әртүрлі мәндеріне сәйкес келетін типтік мысалдардың шешімдерін ұсынайық.
Мысал.
0·x−0=0 сызықтық теңдеуін шешіңіз.
Шешім.
Бұл сызықтық теңдеуде a=0 және b=−0 , ол b=0 сияқты. Демек, бұл теңдеудің шексіз көп түбірі бар; кез келген сан осы теңдеудің түбірі болады.
Жауап:
x – кез келген сан.
Мысал.
0 x + 2,7 = 0 сызықтық теңдеуінің шешімдері бар ма?
Шешім.
Бұл жағдайда а коэффициенті нөлге тең, ал бұл сызықтық теңдеудің b коэффициенті 2,7-ге тең, яғни нөлден өзгеше. Демек, сызықтық теңдеудің түбірі болмайды.
Теңдеулер. Басқаша айтқанда, барлық теңдеулерді шешу осы түрлендірулерден басталады. Сызықтық теңдеулерді шешу кезінде ол (шешім) сәйкестендіру түрлендірулеріне негізделеді және соңғы жауаппен аяқталады.
Белгісіз айнымалы үшін нөлдік емес коэффициент жағдайы.
ax+b=0, a ≠ 0
X бар мүшелерді бір жаққа, ал сандарды екінші жаққа жылжытамыз. Терминдерді теңдеудің қарама-қарсы жағына жылжытқанда таңбаны өзгерту керек екенін есте сақтаңыз:
ax:(a)=-b:(a)
Қысқартып көрейік Асағ Xжәне біз аламыз:
x=-b:(a)
Бұл жауап. Санның бар-жоғын тексеру қажет болса -b:(a)теңдеуіміздің түбірі болса, оның орнына бастапқы теңдеуде ауыстыру керек Xбұл сан:
a(-b:(a))+b=0 (анау. 0=0)
Өйткені онда бұл теңдік дұрыс -b:(a)ал ақиқат – теңдеудің түбірі.
Жауап: x=-b:(a), a ≠ 0.
Бірінші мысал:
5x+2=7x-6
Біз мүшелерді бір жаққа жылжытамыз X, ал екінші жағында сандар:
5х-7х=-6-2
-2x:(-2)=-8:(-2)
Белгісіз фактор үшін біз коэффициентті азайтып, жауап алдық:
Бұл жауап. Егер 4 саны шынымен теңдеудің түбірі екенін тексеру қажет болса, бастапқы теңдеудегі X орнына осы санды қоямыз:
5*4+2=7*4-6 (анау. 22=22)
Өйткені бұл теңдік ақиқат, онда 4 теңдеудің түбірі болады.
Екінші мысал:
Теңдеуді шеш:
5x+14=x-49
Белгісіз сандар мен сандарды әртүрлі бағытта жылжыту арқылы біз мыналарды алдық:
Теңдеудің бөліктерін at коэффициентіне бөліңіз x(4 бойынша) және біз аламыз:
![]()
Үшінші мысал:
Теңдеуді шеш:
![]()
Біріншіден, біз барлық мүшелерді келесіге көбейту арқылы белгісіздік коэффициентіндегі иррационалдықтан құтыламыз:
![]()
![]()
Бұл пішін жеңілдетілген болып саналады, өйткені санның бөлгіштегі санның түбірі болады. Біз алым мен бөлгішті бірдей санға көбейту арқылы жауапты жеңілдетуіміз керек, бізде мыналар бар:
![]()
Шешімдердің жоқтығы.
Теңдеуді шеш:
2x+3=2x+7
Барлығының алдында xтеңдеуіміз шынайы теңдікке айналмайды. Яғни, біздің теңдеуіміздің түбірі жоқ.
Жауап: шешімдер жоқ.
Ерекше жағдай - шешімдердің шексіз саны.
Теңдеуді шеш:
2x+3=2x+3
Х пен сандарды әртүрлі бағытта жылжытып, ұқсас мүшелерді қоссақ, теңдеуді аламыз:
Мұнда да екі бөлікті де 0-ге бөлу мүмкін емес, өйткені тыйым салынған. Дегенмен, орнына қою Xкез келген сан, дұрыс теңдікті аламыз. Яғни, әрбір сан осындай теңдеудің шешімі болып табылады. Осылайша, шешімдердің шексіз саны бар.
Жауабы: шешімдердің шексіз саны.
Екі толық форманың теңдігі жағдайы.
ax+b=cx+d
ax-cx=d-b
(a-c)x=d-b
x=(d-b):(a-c)
Жауап: x=(d-b):(a-c), Егер d≠b және a≠c, әйтпесе шексіз көп шешімдер бар, бірақ егер a=c, А d≠b, онда шешімдер жоқ.
Бұл бейнеде біз бір алгоритм арқылы шешілетін сызықтық теңдеулердің тұтас жиынтығын талдаймыз - сондықтан олар ең қарапайым деп аталады.
Алдымен анықтап алайық: сызықтық теңдеу дегеніміз не және қайсысы қарапайым деп аталады?
Сызықтық теңдеу - тек бір ғана айнымалысы бар және тек бірінші дәрежелі теңдеу.
Ең қарапайым теңдеу мынаны білдіреді:
Барлық басқа сызықтық теңдеулер алгоритмді пайдаланып ең қарапайымға дейін қысқартылады:
- Бар болса, жақшаларды кеңейтіңіз;
- Айнымалысы бар мүшелерді теңдік белгісінің бір жағына, ал айнымалысы жоқ мүшелерді екінші жағына жылжытыңыз;
- Теңдік белгісінің сол және оң жағына ұқсас мүшелерді беріңіз;
- Алынған теңдеуді $x$ айнымалысының коэффициентіне бөліңіз.
Әрине, бұл алгоритм әрқашан көмектесе бермейді. Өйткені, кейде барлық осы айла-шарғылардан кейін $x$ айнымалысының коэффициенті нөлге тең болып шығады. Бұл жағдайда екі нұсқа болуы мүмкін:
- Теңдеудің шешімі мүлдем жоқ. Мысалы, $0\cdot x=8$ сияқты нәрсе шыққанда, яғни. сол жақта нөл, ал оң жақта нөлден басқа сан. Төмендегі бейнеде біз бұл жағдайдың мүмкін болуының бірнеше себептерін қарастырамыз.
- Шешім - барлық сандар. Бұл мүмкін болатын жалғыз жағдай теңдеу $0\cdot x=0$ конструкциясына келтірілгенде болады. Қандай $x$ ауыстырсақ та, ол бәрібір «нөл нөлге тең» болып шығатыны әбден қисынды, яғни. дұрыс сандық теңдік.
Енді өмірден алынған мысалдар арқылы мұның бәрі қалай жұмыс істейтінін көрейік.
Теңдеулерді шешуге мысалдар
Бүгін біз сызықтық теңдеулермен айналысамыз, тек ең қарапайымдары. Жалпы алғанда, сызықтық теңдеу құрамында бір айнымалы бар кез келген теңдікті білдіреді және ол тек бірінші дәрежеге жетеді.
Мұндай конструкциялар шамамен бірдей жолмен шешіледі:
- Ең алдымен, егер бар болса, жақшаларды кеңейту керек (біздің соңғы мысалдағыдай);
- Содан кейін ұқсас біріктіріңіз
- Соңында, айнымалыны оқшаулаңыз, яғни. айнымалыға байланысты барлық нәрсені - ол қамтылған терминдерді - бір жаққа жылжытыңыз, ал онсыз қалғанның барлығын екінші жағына жылжытыңыз.
Содан кейін, әдетте, алынған теңдіктің әр жағында ұқсастарды беру керек, содан кейін «x» коэффициентіне бөлу ғана қалады, біз түпкілікті жауапты аламыз.
Теориялық тұрғыдан бұл жақсы және қарапайым көрінеді, бірақ іс жүзінде тіпті тәжірибелі орта мектеп оқушылары өте қарапайым сызықтық теңдеулерде қорлайтын қателіктер жібере алады. Әдетте, қателер жақшаларды ашу кезінде немесе «плюс» және «минустарды» есептеу кезінде жасалады.
Сонымен қатар, сызықтық теңдеудің шешімдері мүлдем жоқ немесе шешімі бүкіл сандар сызығы болып табылады, яғни. кез келген сан. Біз бүгінгі сабақта осы нәзіктіктерді қарастырамыз. Бірақ біз, сіз түсінгеніңіздей, ең қарапайым тапсырмалардан бастаймыз.
Қарапайым сызықтық теңдеулерді шешу схемасы
Алдымен, қарапайым сызықтық теңдеулерді шешудің барлық схемасын тағы бір рет жазуға рұқсат етіңіз:
- Бар болса, жақшаларды кеңейтіңіз.
- Біз айнымалыларды оқшаулаймыз, яғни. Біз құрамында «Х» бар барлық нәрсені бір жағына, ал «Х» жоқ нәрсені екінші жағына жылжытамыз.
- Біз ұқсас терминдерді ұсынамыз.
- Біз бәрін «х» коэффициентіне бөлеміз.
Әрине, бұл схема әрқашан жұмыс істемейді, онда белгілі бір нәзіктіктер мен трюктар бар, енді біз олармен танысамыз.
Қарапайым сызықтық теңдеулердің нақты мысалдарын шешу
№1 тапсырма
Бірінші қадам бізден жақшаларды ашуды талап етеді. Бірақ олар бұл мысалда жоқ, сондықтан біз оларды өткізіп жібереміз осы кезең. Екінші қадамда айнымалыларды оқшаулау керек. Назар аударыңыз: біз тек жеке шарттар туралы айтып отырмыз. Оны жазып алайық:
Біз сол және оң жақта ұқсас шарттарды ұсынамыз, бірақ бұл жерде бұрыннан жасалған. Сондықтан біз төртінші қадамға көшеміз: коэффициентке бөлеміз:
\[\frac(6x)(6)=-\frac(72)(6)\]
Сонымен, біз жауап алдық.
№2 тапсырма
Біз бұл мәселеде жақшаларды көре аламыз, сондықтан оларды кеңейтейік:
Сол жақта да, оң жақта да біз шамамен бірдей дизайнды көреміз, бірақ алгоритмге сәйкес әрекет етейік, яғни. айнымалыларды ажырату:
Міне, кейбір ұқсастары:
Бұл қай тамырда жұмыс істейді? Жауап: кез келген үшін. Сондықтан $x$ кез келген сан деп жаза аламыз.
№3 тапсырма
Үшінші сызықтық теңдеу қызықтырақ:
\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]
Бірнеше жақша бар, бірақ олар ештеңеге көбейтілмейді, олардың алдында жай ғана жазылады әртүрлі белгілер. Оларды бөлшектеп көрейік:
Біз өзімізге белгілі екінші қадамды орындаймыз:
\[-x+x+2x=15-6-12+3\]
Есеп шығарайық:
Біз соңғы қадамды орындаймыз - бәрін «x» коэффициентіне бөлеміз:
\[\frac(2x)(x)=\frac(0)(2)\]
Сызықтық теңдеулерді шешу кезінде есте сақтау керек нәрселер
Тым қарапайым тапсырмаларды елемейтін болсақ, мен мынаны айтқым келеді:
- Жоғарыда айтқанымдай, кез келген сызықтық теңдеудің шешімі бола бермейді – кейде түбірлері болмайды;
- Тамырлар болса да, олардың арасында нөл болуы мүмкін - бұл жерде ешқандай қате жоқ.
Нөл басқалармен бірдей сан; сіз оны ешқандай түрде кемсітпеуіңіз керек немесе егер сіз нөлге ие болсаңыз, онда сіз дұрыс емес нәрсе жасадыңыз деп ойламаңыз.
Тағы бір ерекшелігі жақшалардың ашылуына қатысты. Назар аударыңыз: олардың алдында «минус» болса, біз оны алып тастаймыз, бірақ жақшадағы белгілерді өзгертеміз қарама-қарсы. Содан кейін біз оны стандартты алгоритмдер арқылы аша аламыз: біз жоғарыдағы есептеулерде көргенімізді аламыз.
Осы қарапайым фактіні түсіну сізге орта мектепте ақымақ және ауыр қателіктер жібермеуге көмектеседі, өйткені мұндай әрекеттер әдеттегідей қабылданады.
Күрделі сызықтық теңдеулерді шешу
Күрделі теңдеулерге көшейік. Енді конструкциялар күрделене түседі және әртүрлі түрлендірулерді орындағанда квадраттық функция пайда болады. Дегенмен, біз бұдан қорықпауымыз керек, өйткені егер автордың жоспары бойынша біз сызықтық теңдеуді шешетін болсақ, онда түрлендіру процесінде квадраттық функциясы бар барлық мономалдар жойылады.
№1 мысал
Бірінші қадам жақшаларды ашу екені анық. Мұны өте мұқият жасайық:
Енді құпиялылықты қарастырайық:
\[-x+6((x)^(2))-6((x)^(2))+x=-12\]
Міне, кейбір ұқсастары:
Әлбетте, бұл теңдеудің шешімі жоқ, сондықтан біз оны жауапқа жазамыз:
\[\ештеңе\]
немесе тамыры жоқ.
№2 мысал
Біз бірдей әрекеттерді орындаймыз. Алғашқы қадам:
Айнымалысы бар барлығын солға, ал онсыз оңға жылжытайық:
Міне, кейбір ұқсастары:
Әлбетте, бұл сызықтық теңдеудің шешімі жоқ, сондықтан оны былай жазамыз:
\[\ештеңе\],
немесе тамыры жоқ.
Шешімнің нюанстары
Екі теңдеу де толық шешілген. Мысал ретінде осы екі өрнекті пайдалана отырып, біз ең қарапайым сызықтық теңдеулердің өзінде бәрі соншалықты қарапайым болмауы мүмкін екеніне тағы бір рет көз жеткіздік: не біреу, не ешқайсысы, не шексіз көп түбір болуы мүмкін. Біздің жағдайда біз екі теңдеуді қарастырдық, екеуінің де түбірі жоқ.
Бірақ мен сіздердің назарларыңызды тағы бір фактіге аударғым келеді: жақшалармен қалай жұмыс істеу керек және олардың алдында минус таңбасы болса, оларды қалай ашу керек. Мына өрнекті қарастырыңыз:
Ашпас бұрын барлығын «X»-ке көбейту керек. Назар аударыңыз: көбейтеді әрбір жеке термин. Ішінде екі термин бар - сәйкесінше екі мүше және көбейтілген.
Осы қарапайым болып көрінетін, бірақ өте маңызды және қауіпті түрлендірулер аяқталғаннан кейін ғана жақшаны одан кейін минус белгісі бар деген көзқараспен ашуға болады. Иә, иә: қазір ғана, түрлендірулер аяқталған кезде, жақшалардың алдында минус таңбасы бар екенін есте ұстаймыз, бұл төмендегі барлық жай ғана белгілерді өзгертетінін білдіреді. Сонымен қатар, жақшалардың өзі жоғалады, ең бастысы, алдыңғы «минус» да жоғалады.
Екінші теңдеумен де солай істейміз:
Менің бұл шағын, елеусіз болып көрінетін фактілерге назар аударуым кездейсоқ емес. Өйткені теңдеулерді шешу әрқашан қарапайым әрекеттерді анық және сауатты орындай алмау жоғары сынып оқушыларының маған келіп, осындай қарапайым теңдеулерді шешуді қайтадан үйренуіне әкелетін қарапайым түрлендірулердің тізбегі болып табылады.
Әрине, сіз бұл дағдыларды автоматты түрде шыңдайтын күн келеді. Енді әр жолы сонша түрлендіруді орындаудың қажеті болмайды, барлығын бір жолға жазасыз. Бірақ сіз жаңа ғана үйреніп жатқанда, әр әрекетті бөлек жазуыңыз керек.
Одан да күрделі сызықтық теңдеулерді шешу
Біз қазір шешетін нәрсені ең қарапайым тапсырма деп атауға болмайды, бірақ мағынасы өзгеріссіз қалады.
№1 тапсырма
\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]
Бірінші бөліктегі барлық элементтерді көбейтейік:
Біраз құпиялылық жасайық:
Міне, кейбір ұқсастары:
Соңғы қадамды аяқтаймыз:
\[\frac(-4x)(4)=\frac(4)(-4)\]
Міне, біздің соңғы жауабымыз. Шешу процесінде бізде квадраттық функциясы бар коэффициенттер болғанына қарамастан, олар бір-бірін жойды, бұл теңдеуді квадраттық емес, сызықтық етеді.
№2 тапсырма
\[\сол(1-4х \оң)\сол(1-3х \оң)=6x\сол(2x-1 \оң)\]
Бірінші қадамды мұқият орындап көрейік: бірінші жақшадағы әрбір элементті екіншісінің әрбір элементіне көбейтіңіз. Трансформациядан кейін барлығы төрт жаңа термин болуы керек:
Енді әр мүшедегі көбейтуді мұқият орындайық:
«Х» бар терминдерді солға, ал жоқтарды оңға жылжытайық:
\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]
Міне, ұқсас терминдер:
Біз тағы да түпкілікті жауап алдық.
Шешімнің нюанстары
Бұл екі теңдеу туралы ең маңызды ескертпе мынада: біз бірнеше мүшесі бар жақшаларды көбейте бастағанда, бұл келесі ережеге сәйкес орындалады: біріншіден бірінші мүшені аламыз және әрбір элементпен көбейтеміз екінші; онда бірінші элементтен екінші элементті аламыз да, екіншісінің әрбір элементіне сол сияқты көбейтеміз. Нәтижесінде бізде төрт термин болады.
Алгебралық қосынды туралы
Осы соңғы мысал арқылы мен студенттерге алгебралық қосындының не екенін еске салғым келеді. Классикалық математикада $1-7$ деп қарапайым құрылысты айтамыз: біреуден жетіні шегеріңіз. Алгебрада біз мынаны айтамыз: «бір» санына тағы бір санды, атап айтқанда «минус жеті» санын қосамыз. Алгебралық қосындының қарапайым арифметикалық қосындыдан айырмашылығы осылай.
Барлық түрлендірулерді, әрбір қосу мен көбейтуді орындаған кезде жоғарыда сипатталғанға ұқсас конструкцияларды көре бастайсыз, көпмүшелермен және теңдеулермен жұмыс істеу кезінде сізде алгебрадан қиындықтар болмайды.
Соңында, біз қарастырғандардан да күрделірек болатын тағы бірнеше мысалды қарастырайық және оларды шешу үшін стандартты алгоритмімізді сәл кеңейтуге тура келеді.
Бөлшектері бар теңдеулерді шешу
Мұндай тапсырмаларды шешу үшін біз алгоритмімізге тағы бір қадам қосуымыз керек. Бірақ алдымен алгоритмімізді еске түсіруге рұқсат етіңіз:
- Жақшаларды ашыңыз.
- Бөлек айнымалылар.
- Ұқсастарын әкеліңіз.
- Пропорцияға бөліңіз.
Өкінішке орай, бұл керемет алгоритм, оның барлық тиімділігіне қарамастан, алдымызда фракциялар болған кезде мүлдем сәйкес келмейді. Төменде көретінімізде екі теңдеуде де сол жақта да, оң жақта да бөлшек бар.
Бұл жағдайда қалай жұмыс істеу керек? Иә, бұл өте қарапайым! Мұны істеу үшін алгоритмге тағы бір қадам қосу керек, оны бірінші әрекетке дейін де, кейін де жасауға болады, атап айтқанда, фракциялардан құтылу. Сонымен, алгоритм келесідей болады:
- Бөлшектерден арылыңыз.
- Жақшаларды ашыңыз.
- Бөлек айнымалылар.
- Ұқсастарын әкеліңіз.
- Пропорцияға бөліңіз.
«Бөлшектерден құтылу» деген нені білдіреді? Неліктен мұны бірінші стандартты қадамнан кейін де, оған дейін де жасауға болады? Шын мәнінде, біздің жағдайда, барлық бөлшектер олардың бөлгішінде сандық болып табылады, яғни. Барлық жерде деноминатор жай ғана сан. Сондықтан теңдеудің екі жағын да осы санға көбейтсек, бөлшектерден құтыламыз.
№1 мысал
\[\frac(\left(2x+1 \оң)\сол(2x-3 \оң))(4)=((x)^(2))-1\]
Осы теңдеудегі бөлшектерден құтылайық:
\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \оң)\cdot 4\]
Назар аударыңыз: бәрі бір рет «төртке» көбейтіледі, яғни. Сізде екі жақша бар болғандықтан, әрқайсысын «төртке» көбейту керек дегенді білдірмейді. Жазып көрейік:
\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]
Енді кеңейтейік:
Біз айнымалыны ажыратамыз:
Біз ұқсас терминдерді қысқартуды орындаймыз:
\[-4x=-1\сол| :\сол(-4 \оң) \оң.\]
\[\frac(-4x)(-4)=\frac(-1)(-4)\]
Біз соңғы шешімді алдық, екінші теңдеуге көшейік.
№2 мысал
\[\frac(\left(1-x \right)\left(1+5x \right))(5)+(x)^(2))=1\]
Мұнда біз бірдей әрекеттерді орындаймыз:
\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]
\[\frac(4x)(4)=\frac(4)(4)\]
Мәселе шешілді.
Шын мәнінде, мен бүгін сізге айтқым келгені осы болды.
Негізгі нүктелер
Негізгі қорытындылар:
- Сызықтық теңдеулерді шешу алгоритмін білу.
- Жақшаларды ашу мүмкіндігі.
- Көрсеңіз, уайымдамаңыз квадраттық функциялар, ең алдымен, одан әрі қайта құру процесінде олар азаяды.
- Сызықтық теңдеулерде түбірлердің үш түрі бар, тіпті ең қарапайымдары да бар: бір түбір, бүкіл сан сызығы түбір, түбірі мүлде болмайды.
Бұл сабақ қарапайым, бірақ барлық математиканы одан әрі түсіну үшін өте маңызды тақырыпты меңгеруге көмектеседі деп үміттенемін. Егер бірдеңе түсініксіз болса, сайтқа өтіп, онда келтірілген мысалдарды шешіңіз. Бізде болыңыз, сізді әлі көптеген қызықты нәрселер күтеді!
 Ұлы Тартария - Ресей империясы Адамзаттың ежелгі тарихы туралы
Ұлы Тартария - Ресей империясы Адамзаттың ежелгі тарихы туралы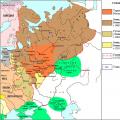 Князь Иван Васильевич 1472 ж
Князь Иван Васильевич 1472 ж «А.П.Платоновтың «Белгісіз гүл» әңгімесі (шағын шолу). Андрей Платоновтың «Белгісіз гүл» әңгімесі туралы «Белгісіз гүл» маған нағыз ертегі нені үйретті
«А.П.Платоновтың «Белгісіз гүл» әңгімесі (шағын шолу). Андрей Платоновтың «Белгісіз гүл» әңгімесі туралы «Белгісіз гүл» маған нағыз ертегі нені үйретті