Тұрақты шамалардың вариациясы. ODE
Дәріс 44. Екінші ретті сызықтық біртекті емес теңдеулер. Еркін константаларды вариациялау әдісі. Тұрақты коэффициенттері бар екінші ретті сызықтық біртекті емес теңдеулер. (арнайы оң жақ).
Әлеуметтік трансформациялар. Мемлекет және шіркеу.
Әлеуметтік саясатБольшевиктер негізінен олардың таптық көзқарастарымен болды. 1917 жылғы 10 қарашадағы жарлықпен таптық жүйе жойылды, революцияға дейінгі шен, атақ, марапаттар жойылды. Судьяларды сайлау белгіленді; азаматтық мемлекеттерді секуляризациялау жүргізілді. Тегін білім беру және медициналық көмек белгіленді (1918 ж. 31 қазандағы жарлық). Әйелдерге ерлермен тең құқықтар берілді (1917 ж. 16 және 18 желтоқсандағы жарлықтар). Неке туралы Жарлық азаматтық неке институтын енгізді.
Халық Комиссарлар Кеңесінің 1918 жылғы 20 қаңтардағы қаулысымен шіркеу мемлекеттен және оқу жүйесінен бөлініп шықты. Шіркеу мүлкінің көп бөлігі тәркіленді. Мәскеу және Бүкіл Русь Патриархы Тихон (1917 жылы 5 қарашада сайланды) 1918 жылы 19 қаңтарда Кеңес өкіметін анатематизациялап, большевиктерге қарсы күреске шақырды.
Сызықтық біртекті емес екінші ретті теңдеуді қарастырайық
Мұндай теңдеудің жалпы шешімінің құрылымы келесі теоремамен анықталады:
Теорема 1.Біртекті емес теңдеудің жалпы шешімі (1) осы теңдеудің кейбір нақты шешімі мен сәйкес біртекті теңдеудің жалпы шешімінің қосындысы ретінде берілген.
Дәлелдеу. соманы дәлелдеу қажет
Сонда бар ортақ шешімтеңдеу (1). Алдымен (3) функциясының (1) теңдеуінің шешімі екенін дәлелдеейік.
(1) теңдеуінің орнына қосындыны қою сағ, бар болады
(2) теңдеудің шешімі бар болғандықтан, бірінші жақшадағы өрнек бірдей нөлге тең. (1) теңдеудің шешімі болғандықтан, екінші жақшадағы өрнек тең f(x). Демек, теңдік (4) сәйкестік болып табылады. Осылайша, теореманың бірінші бөлімі дәлелденді.
Екінші тұжырымды дәлелдеп көрейік: (3) өрнек жалпы(1) теңдеудің шешімі. Бұл өрнекке енгізілген ерікті тұрақтыларды бастапқы шарттар орындалатындай етіп таңдауға болатынын дәлелдеу керек:
сандар қандай болса да x 0 , y 0және (егер ғана x 0функциялары орындалатын аумақтан алынды а 1, а 2Және f(x)үздіксіз).
түрінде ұсынылуы мүмкін екенін байқап. Содан кейін (5) шарттарға сүйене отырып, бізде болады
Осы жүйені шешіп, анықтайық C 1Және C 2. Жүйені келесі түрде қайта жазайық:
Бұл жүйенің анықтаушысы функциялар үшін Вронски анықтаушысы екенін ескеріңіз 1-деЖәне 2-денүктесінде x=x 0. Бұл функциялар шарт бойынша сызықты тәуелсіз болғандықтан, Вронски анықтауышы нөлге тең емес; сондықтан (6) жүйенің белгілі шешімі бар C 1Және C 2, яғни. мұндай мағыналар бар C 1Және C 2, бұл формула бойынша (3) берілген бастапқы шарттарды қанағаттандыратын (1) теңдеудің шешімін анықтайды. Q.E.D.
Біртекті емес теңдеудің жеке шешімдерін табудың жалпы әдісіне көшейік.
Біртекті (2) теңдеудің жалпы шешімін жазайық.
Біртекті емес теңдеудің (1) нақты шешімін (7) түрінде іздейміз. C 1Және C 2кейбір әлі белгісіз функциялар сияқты X.
Теңдікті ажыратайық (7):
Сіз іздеген функцияларды таңдайық C 1Және C 2теңдік сақталады
Егер осы қосымша шартты ескерсек, онда бірінші туынды пішінді қабылдайды
Енді осы өрнекті ажырата отырып, біз мынаны табамыз:
(1) теңдеуге қойып, аламыз
Алғашқы екі жақшадағы өрнектер нөлге айналады, өйткені ж 1Және ж 2– біртекті теңдеудің шешімдері. Демек, соңғы теңдік пішінді қабылдайды
Осылайша, (7) функциясы біртекті емес теңдеудің (1) шешімі болады, егер функциялары болса C 1Және C 2(8) және (9) теңдеулерін орындаңыз. (8) және (9) теңдеулерінен теңдеулер жүйесін құрайық.
Бұл жүйенің детерминанты сызықты тәуелсіз шешімдер үшін Вронски анықтаушысы болғандықтан ж 1Және ж 2теңдеу (2), онда ол нөлге тең емес. Сондықтан жүйені шеше отырып, біз белгілі бір функциялардың екеуін де табамыз X:
Бұл жүйені шеше отырып, интегралдау нәтижесінде -ті қайдан аламыз. Әрі қарай табылған функцияларды формулаға ауыстырамыз, біртекті емес теңдеудің жалпы шешімін аламыз, мұндағы ерікті тұрақтылар.
Біртекті емес дифференциалдық теңдеулерді шешу үшін ерікті тұрақтыларды вариациялау әдісі қолданылады. Бұл сабақ тақырыпты азды-көпті меңгерген студенттерге арналған. Егер сіз қашықтан басқару құралымен танысуды енді бастасаңыз, яғни. Егер сіз шәйнек болсаңыз, мен бірінші сабақтан бастауды ұсынамын: Бірінші ретті дифференциалдық теңдеулер. Шешімдердің мысалдары. Ал егер сіз қазірдің өзінде аяқтап жатсаңыз, әдіс қиын деген болжамды алып тастаңыз. Өйткені бұл қарапайым.
Ерікті константаларды вариациялау әдісі қандай жағдайларда қолданылады?
1) Шешу үшін ерікті тұрақты шаманы өзгерту әдісін қолдануға болады 1-ші ретті сызықтық біртекті емес ДЭ. Теңдеу бірінші ретті болғандықтан, тұрақты да бір болады.
2) Кейбіреулерді шешу үшін ерікті тұрақтылардың вариация әдісі қолданылады сызықты біртекті емес екінші ретті теңдеулер. Мұнда екі тұрақты өзгереді.
Сабақ екі абзацтан тұрады деп есептеу қисынды... Сондықтан мен бұл сөйлемді жаздым және шамамен 10 минут бойы мен практикалық мысалдарға бірқалыпты өту үшін тағы қандай ақылды ақымақтық қосуға болатынын ойладым. Бірақ қандай да бір себептермен менде демалыстан кейін ешқандай ой жоқ, бірақ мен ештеңені теріс пайдаланбаған сияқтымын. Сондықтан бірінші абзацқа көшейік.
Ерікті тұрақты шаманы өзгерту әдісі
бірінші ретті сызықтық біртекті емес теңдеу үшін
Ерікті тұрақты шаманың өзгеру әдісін қарастырмас бұрын мақаламен танысқан жөн. Бірінші ретті сызықтық дифференциалдық теңдеулер. Сол сабақта біз жаттығу жасадық бірінші шешімбіртекті емес 1-ші ретті DE. Бұл бірінші шешім, еске саламын, деп аталады ауыстыру әдісінемесе Бернулли әдісі(шатастыруға болмайды Бернулли теңдеуі!!!)
Енді қараймыз екінші шешім– ерікті тұрақты шаманы өзгерту әдісі. Мен үш-ақ мысал келтіремін, жоғарыда аталған сабақтан алайын. Неге сонша аз? Өйткені шын мәнінде екінші жолдағы шешім бірінші жолдағы шешімге өте ұқсас болады. Сонымен қатар, менің бақылауларым бойынша, ерікті тұрақтыларды вариациялау әдісі ауыстыру әдісіне қарағанда сирек қолданылады.
1-мысал
![]()
(Сабақтың №2 мысалынан айырмашылығы 1-ші ретті сызықтық біртекті емес дифференциалдық теңдеулер)
Шешімі:Бұл теңдеу сызықты біртекті емес және таныс түрі бар: ![]()
Бірінші кезеңде қарапайым теңдеуді шешу қажет: ![]()
Яғни, біз ақымақтықпен оң жағын қалпына келтіреміз және оның орнына нөлді жазамыз.
теңдеу ![]() Мен қоңырау шаламын көмекші теңдеу.
Мен қоңырау шаламын көмекші теңдеу.
Бұл мысалда келесі көмекші теңдеуді шешу керек:
Біздің алдымызда бөлінетін теңдеу, оның шешімі (мен сенемін) енді сіз үшін қиын емес: 
Осылайша: ![]() – көмекші теңдеудің жалпы шешімі.
– көмекші теңдеудің жалпы шешімі.
Екінші қадамда ауыстырамызкейбір тұрақты әзірше«x»-қа тәуелді белгісіз функция:
Осыдан әдістің атауы - тұрақтыны өзгертеміз. Немесе тұрақты мән қазір табуымыз керек функция болуы мүмкін.
IN түпнұсқабіртекті емес теңдеу ![]() ауыстыру жасайық:
ауыстыру жасайық:
және ауыстырайық ![]() теңдеуге
теңдеуге ![]() :
:
Басқару нүктесі – сол жақтағы екі термин күшін жояды. Егер бұл орын алмаса, жоғарыдағы қатені іздеу керек.
Ауыстыру нәтижесінде ажыратылатын айнымалылары бар теңдеу алынды. Біз айнымалыларды бөліп, біріктіреміз.
Қандай жақсылық, көрсеткішті де жояды:
Табылған функцияға «қалыпты» тұрақтыны қосамыз:
Қосулы соңғы кезеңБіздің ауыстыруымызды еске түсірейік:
Функция жаңа ғана табылды!
Сонымен, жалпы шешім: 
Жауап:ортақ шешім: ![]()
Егер сіз екі шешімді басып шығарсаңыз, екі жағдайда да бірдей интегралдарды тапқанымызды оңай байқайсыз. Жалғыз айырмашылық шешім алгоритмінде.
Енді күрделірек нәрсе үшін мен екінші мысалға да түсініктеме беремін:
2-мысал
Дифференциалдық теңдеудің жалпы шешімін табыңыз ![]()
(Сабақтың №8 мысалынан айырмашылығы 1-ші ретті сызықтық біртекті емес дифференциалдық теңдеулер)
Шешімі:Теңдеуді пішінге келтірейік ![]() :
:
Оң жағын қалпына келтіріп, көмекші теңдеуді шешейік:
Көмекші теңдеудің жалпы шешімі:
Біртекті емес теңдеуде ауыстыруды жасаймыз:
Өнімді саралау ережесіне сәйкес: ![]()
және ауыстырайық ![]() бастапқы біртекті емес теңдеуге:
бастапқы біртекті емес теңдеуге:
Сол жақтағы екі термин жойылады, бұл біз дұрыс жолда екенімізді білдіреді: 
Бөлімшелер бойынша біріктірейік. Бөлшектер формуласы бойынша интеграцияның дәмді әріпі шешімге қосылған, сондықтан біз, мысалы, «a» және «be» әріптерін қолданамыз:
![]()
Енді ауыстыруды еске түсірейік:
Жауап:ортақ шешім:
Және бір мысал тәуелсіз шешім:
3-мысал
Берілген бастапқы шартқа сәйкес дифференциалдық теңдеудің нақты шешімін табыңыз.
,
(Сабақтың №4 мысалынан айырмашылығы 1-ші ретті сызықтық біртекті емес дифференциалдық теңдеулер)
Шешімі:
Бұл DE сызықтық біртекті емес. Біз ерікті тұрақтылардың вариация әдісін қолданамыз. Көмекші теңдеуді шешейік:
Біз айнымалыларды бөліп, біріктіреміз: 
Ортақ шешім: ![]()
Біртекті емес теңдеуде ауыстыруды жасаймыз: ![]()
Ауыстыруды орындайық: 
Сонымен, жалпы шешім: ![]()
Берілген бастапқы шартқа сәйкес нақты шешімді табайық: ![]()
Жауап:жеке шешім:
Сабақтың соңындағы шешім тапсырманы орындауға мысал бола алады.
Еркін константаларды вариациялау әдісі
сызықты біртекті емес екінші ретті теңдеу үшін
тұрақты коэффициенттері бар
Екінші ретті теңдеу үшін ерікті тұрақтыларды өзгерту әдісі оңай емес деген пікірді жиі естідім. Бірақ мен мынаны болжаймын: бұл әдіс көбіне қиын болып көрінеді, өйткені ол жиі бола бермейді. Бірақ іс жүзінде ешқандай ерекше қиындықтар жоқ - шешімнің барысы анық, ашық және түсінікті. Және әдемі.
Әдістемені меңгеру үшін біртекті емес екінші ретті теңдеулерді оң жақтың пішініне негізделген белгілі бір шешімді таңдау арқылы шеше білу қажет. Бұл әдіс мақалада егжей-тегжейлі талқыланады. Біртекті емес 2-ші ретті ДС. Тұрақты коэффициенттері бар екінші ретті сызықтық біртекті емес теңдеудің келесі түрі бар екенін еске түсіреміз:
Жоғарыдағы сабақта талқыланған таңдау әдісі оң жағында көпмүшеліктер, экспоненциалдар, синустар және косинустар болған жағдайда ғана жұмыс істейді. Бірақ оң жақта, мысалы, бөлшек, логарифм, тангенс болған кезде не істеу керек? Мұндай жағдайда тұрақты шамаларды өзгерту әдісі көмекке келеді.
4-мысал
Екінші ретті дифференциалдық теңдеудің жалпы шешімін табыңыз ![]()
Шешімі:Бұл теңдеудің оң жағында бөлшек бар, сондықтан белгілі бір шешімді таңдау әдісі жұмыс істемейді деп бірден айта аламыз. Біз ерікті тұрақтылардың вариация әдісін қолданамыз.
Найзағайдың белгілері жоқ, шешімнің басталуы әдеттегідей:
Біз табамыз ортақ шешімқолайлы біртектітеңдеулер: ![]()
Сипаттамалық теңдеуді құрайық және шешейік: ![]()
![]() – конъюгаттық күрделі түбірлер алынады, сондықтан жалпы шешім:
– конъюгаттық күрделі түбірлер алынады, сондықтан жалпы шешім:
Жалпы шешімнің жазбасына назар аударыңыз - егер жақшалар болса, оларды ашыңыз.
Енді біз бірінші ретті теңдеудегідей трюк жасаймыз: тұрақты мәндерді белгісіз функциялармен ауыстырамыз. Яғни, біртекті еместердің жалпы ерітіндісімына түрдегі теңдеулерді іздейміз:
Қайда - әзіршебелгісіз функциялар.

Бұл тұрмыстық қоқыс үйіндісіне ұқсайды, бірақ қазір бәрін реттейміз.
Белгісіздер функциялардың туындылары болып табылады. Біздің мақсатымыз – туындыларды табу, ал табылған туындылар жүйенің бірінші және екінші теңдеулерін де қанағаттандыруы керек.
«Гректер» қайдан шыққан? Лейлек оларды әкеледі. Біз бұрын алынған жалпы шешімді қарастырамыз және жазамыз:
Туындыларды табайық:
Сол жақ бөліктер қарастырылды. Оң жақта не бар?
бастапқы теңдеудің оң жағы, бұл жағдайда:
Коэффицент – екінші туындының коэффициенті:
Іс жүзінде, әрқашан дерлік, және біздің мысал ерекшелік емес.
Барлығы түсінікті, енді сіз жүйені жасай аласыз: 
Жүйе әдетте шешіледі Крамер формулалары бойыншастандартты алгоритмді қолдану. Жалғыз айырмашылығы, бізде сандардың орнына функциялар бар.
Жүйенің негізгі анықтауышын табайық: 
Егер сіз екі-екі анықтауыштың қалай ашылатынын ұмытып қалсаңыз, сабақты қараңыз Анықтаушыны қалай есептеу керек?Сілтеме ұят тақтасына апарады =)
Сонымен: бұл жүйенің бірегей шешімі бар екенін білдіреді.
Туындыны табу: 
Бірақ бұл бәрі емес, әзірге біз тек туындыны таптық.
Функцияның өзі интеграция арқылы қалпына келтіріледі:
Екінші функцияны қарастырайық: 
![]()
![]()
Мұнда біз «қалыпты» тұрақтыны қосамыз
Шешімнің соңғы кезеңінде біртекті емес теңдеудің жалпы шешімін қандай формада іздегеніміз есімізде? Мұндайда:
Сізге қажет функциялар енді ғана табылды! ![]()
Бар болғаны ауыстыруды орындау және жауапты жазу:
Жауап:ортақ шешім:
Негізінде, жауап жақшаларды кеңейте алар еді.
Жауапты толық тексеру сабақта талқыланған типтік схема бойынша жүзеге асырылады. Біртекті емес 2-ші ретті ДС. Бірақ тексеру оңай болмайды, өйткені өте ауыр туындыларды тауып, ауыр ауыстыруды жүзеге асыру қажет. Мұндай диффузорларды шешкен кезде бұл жағымсыз қасиет.
5-мысал
Ерікті тұрақтыларды өзгерту арқылы дифференциалдық теңдеуді шешіңіз
![]()
Бұл өз бетіңізше шешуге болатын мысал. Шындығында, оң жағында да бөлшек бар. Еске алайық тригонометриялық формула, айтпақшы, оны шешу кезінде қолдану қажет болады.
Ерікті константаларды вариациялау әдісі ең әмбебап әдіс болып табылады. Ол шешуге болатын кез келген теңдеуді шеше алады оң жақтың пішініне негізделген белгілі бір шешімді таңдау әдісі. Сұрақ туындайды: неге онда да ерікті тұрақтыларды өзгерту әдісін қолданбасқа? Жауап анық: сыныпта талқыланған белгілі бір шешімді таңдау Біртекті емес екінші ретті теңдеулер, шешімді айтарлықтай жылдамдатады және жазбаны қысқартады - детерминанттар мен интегралдармен әбігерге түсуге болмайды.
көмегімен екі мысалды қарастырайық Коши мәселесі.
6-мысал
Берілген бастапқы шарттарға сәйкес дифференциалдық теңдеудің нақты шешімін табыңыз
![]() ,
, ![]()
Шешімі:Қайтадан бөлшек және көрсеткіш қызықты жер.
Біз ерікті тұрақтылардың вариация әдісін қолданамыз.
Біз табамыз ортақ шешімқолайлы біртектітеңдеулер: ![]()
![]() – әртүрлі нақты түбірлер алынады, сондықтан жалпы шешім:
– әртүрлі нақты түбірлер алынады, сондықтан жалпы шешім:
Біртекті еместердің жалпы ерітіндісітеңдеулерді мына түрде іздейміз: , мұндағы – әзіршебелгісіз функциялар.
Жүйені құрайық: 
Бұл жағдайда:
,
Туындыларды табу: ![]() ,
, ![]()
![]()
Осылайша: 
Крамер формулалары арқылы жүйені шешейік:
, бұл жүйеде бірегей шешім бар дегенді білдіреді.


Функцияны біріктіру арқылы қалпына келтіреміз:
Мұнда қолданылған функцияны дифференциалдық таңбаға қосу әдісі.


Екінші функцияны интеграция арқылы қалпына келтіреміз: ![]()
Бұл интеграл шешілді ауыспалы ауыстыру әдісі:
Ауыстырудың өзінен біз мынаны білдіреміз:
Осылайша: ![]()
![]()
Бұл интегралды табуға болады толық квадратты алу әдісі, бірақ диффузорлары бар мысалдарда мен фракцияны кеңейтуді қалаймын әдіс белгісіз коэффициенттер
:
Екі функция да табылды:
Нәтижесінде біртекті емес теңдеудің жалпы шешімі:
Бастапқы шарттарды қанағаттандыратын нақты шешімді табайық ![]() .
.
Техникалық тұрғыдан алғанда, шешімді іздеу мақалада талқыланған стандартты түрде жүзеге асырылады Екінші ретті біртекті емес дифференциалдық теңдеулер.
Күте тұрыңыз, енді біз жалпы шешімнің туындысын табамыз:
Бұл сондай масқара. Оны оңайлатудың қажеті жоқ, теңдеулер жүйесін бірден құру оңайырақ. Бастапқы шарттарға сәйкес ![]() :
:

Тұрақтылардың табылған мәндерін ауыстырайық ![]() жалпы шешімге:
жалпы шешімге:
Жауапта логарифмдерді аздап толтыруға болады.
Жауап:жеке шешім: ![]()
Көріп отырғаныңыздай, интегралдар мен туындыларда қиындықтар туындауы мүмкін, бірақ ерікті тұрақтылардың вариация әдісінің алгоритмінде емес. Сізді қорқытқан мен емес, бәрі Кузнецовтың жинағы!
Релаксация үшін оны өзіңіз шешудің соңғы, қарапайым мысалы:
7-мысал
Коши есебін шешу
![]() ,
, ![]()
Мысал қарапайым, бірақ креативті, жүйені жасаған кезде шешім қабылдамас бұрын оны мұқият қараңыз ;-),
![]()


![]()
Нәтижесінде, жалпы шешім:
Бастапқы шарттарға сәйкес келетін нақты шешімді табайық ![]() .
.
![]()

Тұрақтылардың табылған мәндерін жалпы шешімге ауыстырайық:
Жауап:жеке шешім:
Бірінші ретті сызықтық дифференциалдық теңдеулер мен Бернулли теңдеуін шешудің тағы бір жолы еркін тұрақты шаманы өзгерту әдісі немесе Лагранж әдісі болып табылады.
Бірінші ретті сызықтық дифференциалдық теңдеулер y’+p(x)y=q(x) түріндегі теңдеулер. Оң жағында нөл болса: y’+p(x)y=0, онда бұл сызықтық біртекті 1-ші ретті теңдеу. Сәйкесінше, оң жағы нөлге тең емес теңдеу, y’+p(x)y=q(x), гетерогенді 1-ші ретті сызықтық теңдеу.
Ерікті тұрақты шаманы өзгерту әдісі (Лагранж әдісі) келесідей:
1) y’+p(x)y=0: y=y* біртекті теңдеуінің жалпы шешімін іздейміз.
2) Жалпы шешімде С-ны тұрақты емес, х-тің функциясы деп қарастырамыз: С = С (х). Жалпы шешімнің туындысын (y*)’ тауып, алынған өрнекті y* және (y*)’ орнына бастапқы шартқа қоямыз. Алынған теңдеуден C(x) функциясын табамыз.
3) Біртекті теңдеудің жалпы шешімінде С орнына табылған С(х) өрнегін қоямыз.
Ерікті тұрақты шаманы өзгерту әдісінің мысалдарын қарастырайық. Төмендегідей тапсырмаларды қабылдап, шешімнің орындалу барысын салыстырып, алынған жауаптардың сәйкес келетініне көз жеткізейік.
1) y’=3x-y/x
Теңдеуді стандартты түрде қайта жазайық (Бернулли әдісінен айырмашылығы, мұнда теңдеудің сызықтық екенін көру үшін ғана белгілеу формасы қажет болды).
y’+y/x=3x (I). Енді біз жоспар бойынша жүреміз.
1) y’+y/x=0 біртекті теңдеуін шешіңіз. Бұл бөлінетін айнымалылары бар теңдеу. y’=dy/dx деп елестетіңіз, ауыстырыңыз: dy/dx+y/x=0, dy/dx=-y/x. Теңдеудің екі жағын да dx-ке көбейтіп, xy≠0-ге бөлеміз: dy/y=-dx/x. Біріктірейік:
2) Біртекті теңдеудің нәтижесінде алынған жалпы шешімде С тұрақты емес, х-тің функциясын қарастырамыз: C=C(x). Осы жерден
Алынған өрнектерді шартқа (I) ауыстырамыз:
Теңдеудің екі жағын да интегралдаймыз:
мұнда C қазірдің өзінде жаңа тұрақты болып табылады.
3) y=C/x біртекті теңдеуінің жалпы шешімінде C=C(x), яғни y=C(x)/x деп қабылдағанбыз, C(x) орнына табылған x³ өрнегін қоямыз. +C: y=(x³ +C)/x немесе y=x²+C/x. Бернулли әдісімен шешу кезіндегідей жауап алдық.
Жауабы: y=x²+C/x.
2) y’+y=cosx.
Мұнда теңдеу стандартты түрде жазылған, оны түрлендірудің қажеті жоқ.
1) y’+y=0 біртекті сызықтық теңдеуді шешіңіз: dy/dx=-y; dy/y=-dx. Біріктірейік:
Белгілеудің ыңғайлы түрін алу үшін біз С дәрежесінің көрсеткішін жаңа С ретінде аламыз:
Бұл түрлендіру туындыны табу ыңғайлы болу үшін жасалды.
2) Сызықты біртекті теңдеудің нәтижесінде алынған жалпы шешімде С тұрақты емес, х-тің функциясы деп есептейміз: C=C(x). Осы шарт бойынша
![]()
Алынған у және у’ өрнектерін шартқа ауыстырамыз:
Теңдеудің екі жағын көбейтіңіз
Бөлшектері бойынша интегралдау формуласын пайдаланып теңдеудің екі жағын да интегралдаймыз, мынаны аламыз:
Мұндағы С енді функция емес, кәдімгі тұрақты.
3) Біртекті теңдеудің жалпы шешімінде
табылған C(x) функциясын ауыстырыңыз:
Бернулли әдісімен шешу кезіндегідей жауап алдық.
Шешу үшін ерікті тұрақты шаманы өзгерту әдісі де қолданылады.
y'x+y=-xy².
Теңдеуді стандартты түрге келтіреміз: y’+y/x=-y² (II).
1) y’+y/x=0 біртекті теңдеуін шешіңіз. dy/dx=-y/x. Теңдеудің екі жағын да dx-ке көбейтіп, у-ға бөлеміз: dy/y=-dx/x. Енді біріктірейік:
Алынған өрнектерді шартқа (II) ауыстырамыз:
Жеңілдетейік:
![]()
Біз C және x үшін бөлінетін айнымалылары бар теңдеу алдық:
![]()
![]()
Мұндағы C қазірдің өзінде кәдімгі тұрақты. Интегралдау процесі кезінде біз белгілерді шамадан тыс жүктемеу үшін C(x) орнына жай ғана C деп жаздық. Соңында біз C(x)-ті жаңа С-мен шатастырмау үшін С(x)-ға оралдық.
3) y=C(x)/x біртекті теңдеуінің жалпы шешімінде табылған C(x) функциясын ауыстырамыз:
![]()
Бернулли әдісімен шешу кезіндегідей жауап алдық.
![]()
Өзін-өзі тексеру мысалдары:
1. Теңдеуді стандартты түрде қайта жазайық: y’-2y=x.
1) y’-2y=0 біртекті теңдеуін шешіңіз. y’=dy/dx, демек dy/dx=2y, теңдеудің екі жағын да dx-ке көбейтіп, у-ға бөліп, интегралдаймыз:
Осы жерден y табамыз:
Шартқа y және y’ өрнектерін қоямыз (қысқалық үшін C(x) орнына C және C"(x) орнына C' қолданамыз):
Оң жақтағы интегралды табу үшін бөліктер бойынша интегралдау формуласын қолданамыз:
![]()
Енді формулаға u, du және v ауыстырамыз:
Мұнда C =const.
3) Енді ерітіндіге біртектіні ауыстырамыз
Лагранж тұрақтыларының вариация әдісімен коэффициенттері тұрақты жоғары ретті сызықтық біртекті емес дифференциалдық теңдеулерді шешу әдісі қарастырылған. Лагранж әдісі кез келген сызықты біртекті емес теңдеулерді шешуге де қолданылады, егер біртекті теңдеуді шешудің негізгі жүйесі белгілі болса.
МазмұныСондай-ақ қараңыз:
Лагранж әдісі (тұрақтылардың өзгеруі)
Ерікті n-ші ретті тұрақты коэффициенттері бар сызықтық біртекті емес дифференциалдық теңдеуді қарастырайық:
(1)
.
Бірінші ретті теңдеу үшін қарастырған тұрақты шаманы өзгерту әдісі жоғары дәрежелі теңдеулер үшін де қолданылады.
Шешім екі кезеңде жүзеге асырылады. Бірінші қадамда біз оң жақ бөлігін алып тастап, біртекті теңдеуді шешеміз. Нәтижесінде n ерікті тұрақтыдан тұратын шешімді аламыз. Екінші кезеңде біз тұрақтыларды өзгертеміз. Яғни, бұл тұрақтылар х тәуелсіз айнымалысының функциялары деп есептейміз және осы функциялардың түрін табамыз.
Бұл жерде тұрақты коэффициенттері бар теңдеулерді қарастырғанымызбен, бірақ Лагранж әдісі кез келген сызықты біртекті емес теңдеулерді шешуге де қолданылады. Бұл үшін біртекті теңдеуді шешудің негізгі жүйесі белгілі болуы керек.
1-қадам. Біртекті теңдеуді шешу
Бірінші ретті теңдеулердегі сияқты, біз алдымен біртекті теңдеудің оң жақ біртекті емес жағын нөлге теңестіріп, жалпы шешімін іздейміз:
(2)
.
Бұл теңдеудің жалпы шешімі:
(3)
.
Мұнда ерікті тұрақтылар берілген; - осы теңдеудің шешімдерінің іргелі жүйесін құрайтын біртекті (2) теңдеудің n сызықты тәуелсіз шешімдері.
Қадам 2. Тұрақтыларды өзгерту – тұрақтыларды функциялармен ауыстыру
Екінші кезеңде біз тұрақты шамалардың вариациясымен айналысамыз. Басқаша айтқанда, тұрақтыларды х тәуелсіз айнымалысының функцияларымен ауыстырамыз:
.
Яғни, бастапқы (1) теңдеудің келесі түрдегі шешімін іздейміз:
(4)
.
Егер (4) мәнін (1) орнына қойсақ, n функция үшін бір дифференциалдық теңдеу аламыз. Бұл жағдайда бұл функцияларды қосымша теңдеулермен байланыстыра аламыз. Сонда сіз n функцияны анықтауға болатын n теңдеу аласыз. Қосымша теңдеулерді жазуға болады әртүрлі жолдар. Бірақ біз мұны шешімнің қарапайым пішіні болуы үшін жасаймыз. Ол үшін дифференциалдау кезінде функциялардың туындылары бар мүшелерді нөлге теңестіру керек. Осыны көрсетейік.
Ұсынылған шешімді (4) бастапқы (1) теңдеуіне ауыстыру үшін (4) түрінде жазылған функцияның бірінші n ретті туындыларын табу керек. Қосынды мен көбейтіндіні дифференциалдау ережелерін пайдаланып (4) ажыратамыз:
.
Қане, мүшелерді топтастырайық. Алдымен туындылары бар мүшелерді, содан кейін туындылары бар мүшелерді жазамыз:
.
Функцияларға бірінші шартты қояйық:
(5.1)
.
Сонда бірінші туындыға қатысты өрнек қарапайымырақ пішінге ие болады:
(6.1)
.
Сол әдісті қолданып, біз екінші туындыны табамыз:
.
Функцияларға екінші шарт қояйық:
(5.2)
.
Содан кейін
(6.2)
.
Тағыда басқа. IN қосымша шарттар, функциясының туындылары бар мүшелерді нөлге теңейміз.
Сонымен, функциялар үшін келесі қосымша теңдеулерді таңдасақ:
(5,к) ,
онда бірінші туындылар ең қарапайым пішінге ие болады:
(6,к) .
Мұнда .
n-ші туындыны табыңыз:
(6.n)
.
Бастапқы теңдеуді (1) ауыстырыңыз:
(1)
;
.
Барлық функциялар (2) теңдеуді қанағаттандыратынын ескерейік:
.
Сонда құрамында нөл бар мүшелердің қосындысы нөлді береді. Нәтижесінде біз аламыз:
(7)
.
Нәтижесінде жүйеге қол жеткіздік сызықтық теңдеулертуындылар үшін:
(5.1)
;
(5.2)
;
(5.3)
;
. . . . . . .
(5.n-1) ;
(7′) .
Бұл жүйені шеше отырып, х-тің функциясы ретінде туындылар үшін өрнектерді табамыз. Интеграциялау арқылы біз мыналарды аламыз:
.
Мұнда x-ке тәуелді емес тұрақтылар берілген. (4) орнына қойып, бастапқы теңдеудің жалпы шешімін аламыз.
Туындылардың мәндерін анықтау үшін біз ешқашан a i коэффициенттерінің тұрақты екендігін пайдаланбағанымызды ескеріңіз. Сондықтан Кез келген сызықты біртекті емес теңдеулерді шешу үшін Лагранж әдісі қолданылады, егер біртекті (2) теңдеудің шешімдерінің іргелі жүйесі белгілі болса.
Мысалдар
Тұрақты шамаларды вариациялау әдісімен (Лагранж) теңдеулерді шешу.
Мысалдар шешімі > > >
Бернулли әдісі арқылы жоғары ретті теңдеулерді шешу
Тұрақты коэффициенттері бар жоғары ретті сызықтық біртекті емес дифференциалдық теңдеулерді сызықтық алмастыру арқылы шешу
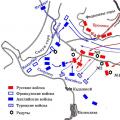 Балаклава шайқасы Балаклава шайқасы
Балаклава шайқасы Балаклава шайқасы Император Павел I және оның сүйікті Иван Павлович Кутаисов
Император Павел I және оның сүйікті Иван Павлович Кутаисов Князь Всеволод III Новгородпен үлкен ұя қатынасы
Князь Всеволод III Новгородпен үлкен ұя қатынасы