R(sin x, cos x) түріндегі рационал функцияларды интегралдау үшін әмбебап тригонометриялық алмастыру деп аталатын алмастыру қолданылады. Содан кейін. Әмбебап тригонометриялық ауыстыру көбінесе үлкен есептеулерге әкеледі. Сондықтан мүмкіндігінше келесі ауыстыруларды пайдаланыңыз.

Тригонометриялық функцияларға рационалды тәуелді функцияларды интегралдау

1. ∫ sin n xdx , ∫ cos n xdx , түріндегі интегралдар n>0
а) Егер n тақ болса, дифференциал таңбасының астына sinx (немесе cosx) бір дәрежесін енгізу керек, ал қалған жұп дәрежеден қарама-қарсы функцияға өту керек.
б) Егер n жұп болса, онда дәрежені азайту үшін формулаларды қолданамыз
2. ∫ tg n xdx , ∫ ctg n xdx түріндегі интегралдар, мұндағы n – бүтін сан.
Формулаларды қолдану керек

3. ∫ sin n x cos m x dx түріндегі интегралдар
а) m және n әр түрлі паритеттік болсын. Егер n тақ болса, t=sin x, m тақ болса, t=cos x алмастыруды қолданамыз.
б) Егер m және n жұп болса, онда дәрежені азайту үшін формулаларды қолданамыз
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Пішіннің интегралдары
Егер m және n сандары бірдей паритет болса, онда t=tg x алмастыруды қолданамыз. Көбінесе тригонометриялық бірлік техникасын қолдану ыңғайлы.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Өнімді түрлендіру формулаларын қолданайық тригонометриялық функцияларолардың мөлшерінде:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Мысалдар
1. ∫ cos 4 x·sin 3 xdx интегралын есептеңдер.
cos(x)=t ауыстыруды жасаймыз. Сонда ∫ cos 4 x sin 3 xdx =
2. Интегралды есептеңдер.
Ауыстыру sin x=t жасай отырып, аламыз

3. Интегралды табыңыз.
tg(x)=t ауыстыруды жасаймыз. Ауыстыру, біз аламыз

R(sinx, cosx) түріндегі интегралдық өрнектер

№1 мысал. Интегралды есептеңіз:

Шешім.
а) R(sinx, cosx) түріндегі өрнектерді интегралдау, мұндағы R - sin x және cos x рационал функциясы, tg(x/2) = t әмбебап тригонометриялық алмастыру арқылы рационал функциялардың интегралдарына түрлендіріледі.
Сонда бізде

Әмбебап тригонометриялық алмастыру ∫ R(sinx, cosx) dx түріндегі интегралдан келесі интегралға көшуге мүмкіндік береді. бөлшек рационал функция, бірақ көбінесе мұндай ауыстыру қолайсыз өрнектерге әкеледі. Белгілі бір жағдайларда қарапайым ауыстырулар тиімді:

• Егер R(-sin x, cos x) = -R(sin x, cos x)dx теңдігі орындалса, онда cos x = t ауыстыру қолданылады.
• Егер R(sin x, -cos x) = -R(sin x, cos x)dx теңдігі орындалса, онда sin x = t алмастыру.
• Егер R(-sin x, -cos x) = R(sin x, cos x)dx теңдігі орындалса, онда алмастыру tgx = t немесе ctg x = t.

Бұл жағдайда интегралды табу керек
tg(x/2) = t әмбебап тригонометриялық алмастыруды қолданайық.
Сонда Жауап:

Антитуындылар кестесі («интегралдар»). Интегралдар кестесі. Кестелік емес анықталған интегралдар. (Ең қарапайым интегралдар және параметрі бар интегралдар). Бөлшектер бойынша интегралдау формулалары. Ньютон-Лейбниц формуласы.

Антитуындылар кестесі («интегралдар»).
Кестелік анықталмаған интегралдар.	Кестелік анықталмаған интегралдар.
(Ең қарапайым интегралдар және параметрі бар интегралдар).
	Дәрежелік функцияның интегралы.
Дифференциалдық таңбаның астына x жүргізілсе, дәрежелік функцияның интегралына келтіретін интеграл.	Көрсеткіштің интегралы, мұндағы a тұрақты сан.
Күрделі көрсеткіштік функцияның интегралы.	Көрсеткіштік функцияның интегралы.
	Көрсеткіштік функцияның интегралы.
Натурал логарифмге тең интеграл.	Интегралдық: «Ұзын логарифм».
Натурал логарифмге тең интеграл.
Интеграл: «Жоғары логарифм».	Алымдағы x дифференциалдық таңбаның астына орналастырылған интеграл (белгі астындағы тұрақтыны қосуға немесе азайтуға болады) ең соңында натурал логарифмге тең интегралға ұқсас.
Косинус интегралы.	Синус интегралы.
Интеграл жанамаға тең.
Котангенске тең интеграл.	Арксинус пен арккосинға тең интеграл
Арксинусқа да, арксинусқа да тең интеграл.	Арктангенс пен арккотангенске тең интеграл.
Косекантқа тең интеграл.	Бөлімге тең интеграл.
Косекантқа тең интеграл.	Косекантқа тең интеграл.
Арксекантқа тең интеграл.	Арккосекантқа тең интеграл.
Гиперболалық синусына тең интеграл.	Гиперболалық косинусқа тең интеграл.
Интеграл гиперболалық синусқа тең, мұндағы sinhx ағылшын тіліндегі нұсқадағы гиперболалық синус.	Интеграл гиперболалық косинусқа тең, мұндағы sinhx ағылшын тіліндегі нұсқадағы гиперболалық синус.
Гиперболалық тангенске тең интеграл.	Гиперболалық котангенске тең интеграл.

Гиперболалық секантқа тең интеграл.

Гиперболалық косекантқа тең интеграл.
Бөлшектер бойынша интегралдау формулалары. Интеграция ережелері.
Функциялар қосындысын интегралдау:
анықталмаған интегралдар:
Бөлшектері бойынша интегралдау формуласы Анықталған интегралдар:
Ньютон-Лейбниц формуласы Анықталған интегралдар:	Мұндағы F(a),F(b) сәйкесінше b және a нүктелеріндегі қарсы туындылардың мәндері.

Туындылар кестесі. Кестелік туындылар. Өнімнің туындысы. Бөлімшенің туындысы. Күрделі функцияның туындысы.

Егер x тәуелсіз айнымалы болса, онда:

Туындылар кестесі. Кестелік туындылар."кесте туындысы" - иә, өкінішке орай, оларды Интернетте дәл осылай іздейді.
	Дәрежелік функцияның туындысы
	Көрсеткіштің туындысы
Күрделі көрсеткіштік функцияның туындысы	Көрсеткіштік функцияның туындысы
Логарифмдік функцияның туындысы	Туынды табиғи логарифм
	Функцияның натурал логарифмінің туындысы
Синустың туындысы	Косинустың туындысы
Косеканттың туындысы	Секанттың туындысы
Арксинус туындысы	Косинус доғасының туындысы
Арксинус туындысы	Косинус доғасының туындысы
Тангенс туындысы	Котангенс туындысы
Арктангенс туындысы	Доға котангенсінің туындысы
Арктангенс туындысы	Доға котангенсінің туындысы
Арксеканттың туындысы	Арккосеканттың туындысы
Арксеканттың туындысы	Арккосеканттың туындысы
Гиперболалық синустың туындысы Ағылшын тіліндегі нұсқадағы гиперболалық синустың туындысы	Гиперболалық косинустың туындысы Ағылшын тіліндегі гиперболалық косинустың туындысы
Гиперболалық тангенстің туындысы	Гиперболалық котангенстің туындысы
Гиперболалық секанттың туындысы	Гиперболалық косеканттың туындысы

Дифференциация ережелері. Өнімнің туындысы. Бөлімшенің туындысы.
Күрделі функцияның туындысы.
Тұрақты шама арқылы туындының (функцияның) туындысы:
Қосындының туындысы (функция):
Өнімнің туындысы (функциялары):
Бөлімнің (функциялардың) туындысы:

Күрделі функцияның туындысы:

Логарифмдердің қасиеттері. Логарифмдердің негізгі формулалары. Ондық (lg) және натурал логарифмдер (ln).
Негізгі логарифмдік сәйкестік
a b түріндегі кез келген функцияның экспоненциалды қалай жасауға болатынын көрсетейік. e x түріндегі функция көрсеткіштік деп аталатындықтан, онда

a b түріндегі кез келген функция онның дәрежесі ретінде көрсетілуі мүмкін

Натурал логарифм ln (негізгі логарифм e = 2,718281828459045...) ln(e)=1; ln(1)=0

Тейлор сериясы. Функцияның Тейлор қатарын кеңейту. Көпшілік екені белгілі болдыіс жүзінде кездесті

математикалық функцияларды белгілі бір нүктеге жақын жерде айнымалының дәрежелерін өсу ретімен қамтитын дәрежелік қатарлар түрінде кез келген дәлдікпен беруге болады. Мысалы, x=1 нүктесіне жақын жерде: Серияларды пайдаланған кезде шақырыладыҚұрамында алгебралық, тригонометриялық және көрсеткіштік функциялар бар аралас функцияларды таза алгебралық функциялар ретінде көрсетуге болады. Серияларды пайдалана отырып, жиі дифференциация мен интеграцияны жылдам орындауға болады.

a нүктесінің маңайындағы Тейлор қатары келесі пішінге ие:

1) , мұндағы f(x) – x = a кезіндегі барлық ретті туындылары бар функция. R n – Тейлор қатарындағы қалдық мүшесі өрнек арқылы анықталады

2)

Қатардың k-ші коэффициенті (x k кезінде) формуламен анықталады

3) Тейлор сериясының ерекше жағдайы Маклаурин (=McLaren) сериясы болып табылады (кеңейу a=0 нүктесінің айналасында жүреді)

a=0 кезінде

қатардың мүшелері формула бойынша анықталады

Тейлор қатарын қолдану шарттары.

1. f(x) функциясының (-R;R) интервалында Тейлор қатарына кеңеюі үшін бұл үшін Тейлор (Маклаурин (=Мкларен)) формуласындағы қалған мүшесі қажет және жеткілікті. функция көрсетілген интервалда (-R;R) k →∞ ретінде нөлге ұмтылады.

2. Тейлор қатарын тұрғызғалы жатқан жақын нүктеде берілген функция үшін туындылар болуы қажет.

Тейлор қатарының қасиеттері.

Егер f аналитикалық функция болса, онда оның Тейлор қатары f анықтау облысындағы кез келген а нүктесіндегі a-ның кейбір маңайында f-қа жиналады.

Шексіз дифференциалданатын функциялар бар, олардың Тейлор қатарлары жинақталады, бірақ сонымен бірге а-ның кез келген маңындағы функциядан ерекшеленеді. Мысалы:

Тейлор қатарлары жуықтауда қолданылады (апроксимация - ғылыми әдіс, ол кейбір объектілерді басқаларымен ауыстырудан тұрады, бір мағынада немесе басқада бастапқыға жақын, бірақ қарапайым) функцияларды көпмүшелер арқылы. Атап айтқанда, сызықтық жүйені зерттеу сызықтық жүйені талдаумен ауыстырылатын, қандай да бір мағынада бастапқыға тең келетін тұйық сызықты емес жүйелерді жуықтап көрсету әдістерінің бірі - linearization ((linearis - сызықтық) .) теңдеулер Тейлор қатарын кеңейту және бірінші реттегі барлық мүшелерді кесу арқылы пайда болады.

Осылайша, кез келген дерлік функцияны берілген дәлдікпен көпмүше ретінде көрсетуге болады.

Маклаурин қатарындағы (=Макларен, Тейлор 0 нүктесінің маңында) және 1-ші нүктенің маңындағы Тейлордағы қуат функцияларының кейбір жалпы кеңеюлерінің мысалдары. Тейлор және Макларен қатарларындағы негізгі функциялардың кеңеюінің алғашқы мүшелері.

Маклаурин қатарындағы қуат функцияларының кейбір кеңеюлерінің мысалдары (= McLaren, Taylor 0 нүктесінің маңында)

1-тармаққа жақын кейбір кең тараған Тейлор қатарының кеңеюінің мысалдары

Тригонометриялық функциялардың интегралдары.
Шешімдердің мысалдары

Бұл сабақта біз тригонометриялық функциялардың интегралдарын қарастырамыз, яғни интегралдарды толтыру әр түрлі комбинациялардағы синустар, косинустар, тангенстер және котангенстер болады. Барлық мысалдар егжей-тегжейлі, қол жетімді және тіпті шәйнек үшін түсінікті болады.

Тригонометриялық функциялардың интегралдарын табысты зерттеу үшін қарапайым интегралдарды жақсы түсіну керек, сонымен қатар кейбір интегралдау әдістерін меңгеру керек. Сіз бұл материалдармен дәрістерде таныса аласыз Анықталмаған интеграл. Шешімдердің мысалдарыЖәне .

Ал енді бізге қажет: Интегралдар кестесі, Туындылар кестесіЖәне Тригонометриялық формулалар анықтамалығы. Барлығы әдістемелік құралдарбетінде табуға болады Математикалық формулалар мен кестелер. Мен бәрін басып шығаруды ұсынамын. Мен әсіресе тригонометриялық формулаларға назар аударамын, олар сіздің көз алдыңызда болуы керек– онсыз жұмыс тиімділігі айтарлықтай төмендейді.

Бірақ алдымен, бұл мақалада қандай интегралдар туралы Жоқ. Пішіннің интегралдары жоқ, - косинус, синус, кейбір көпмүшеге көбейтілген (тангенсі немесе котангенсі азырақ нәрсе). Мұндай интегралдар бөліктер арқылы интегралданады, ал әдісті үйрену үшін Бөлімшелер бойынша интегралдау сабағына барыңыз. Шешімдердің мысалдары мұнда «доғалары» бар интегралдар жоқ - арктангенс, арксинус және т.б., олар көбінесе бөліктермен біріктірілген.

Тригонометриялық функциялардың интегралдарын табу кезінде бірқатар әдістер қолданылады:

(4) Біз кестелік формуланы қолданамыз , жалғыз айырмашылығы «X» орнына бізде күрделі өрнек бар.

2-мысал

3-мысал

Табу анықталмаған интеграл.

Байқауда батып бара жатқандар үшін жанрдың классикасы. Сіз байқаған боларсыз, интегралдар кестесінде тангенс пен котангенстің интегралы жоқ, бірақ соған қарамастан мұндай интегралдарды табуға болады.

(1) Біз тригонометриялық формуланы қолданамыз

(2) Функцияны дифференциалдық таңбаның астына келтіреміз.

(3) Біз кесте интегралын қолданамыз .

4-мысал

Анықталмаған интегралды табыңыз.

Бұл үшін мысал тәуелсіз шешім, толық шешімі мен жауабы сабақтың соңында.

5-мысал

Анықталмаған интегралды табыңыз.

Біздің дәрежелеріміз біртіндеп көтеріледі =).
Алдымен шешім:

(1) Біз формуланы қолданамыз

(2) Біз негізгі тригонометриялық сәйкестікті қолданамыз , бұдан былай шығады .

(3) Алымды бөлшекті мүшеге бөл.

(4) Анықталмаған интегралдың сызықтық қасиетін қолданамыз.

(5) Кестені пайдаланып біріктіреміз.

6-мысал

Анықталмаған интегралды табыңыз.

Бұл тәуелсіз шешімге мысал, толық шешім мен жауап сабақтың соңында.

Сондай-ақ тангенс пен котангенстің интегралдары бар, олар жоғары дәрежеде болады. Сабақта жанама кубтың интегралы талқыланады Жазық фигураның ауданын қалай есептеуге болады?Төртінші және бесінші дәрежелерге жанама (котангенс) интегралдарын бетте алуға болады. Күрделі интегралдар.

Интегралдың дәрежесін азайту

Бұл әдіс интегралдық функциялар синустар мен косинустармен толтырылған кезде жұмыс істейді тіптіградус. Дәрежені азайту үшін тригонометриялық формулаларды қолданыңыз , және , және соңғы формула көбінесе қарама-қарсы бағытта қолданылады: .

7-мысал

Анықталмаған интегралды табыңыз.

Шешімі:

Негізінде, біз формуланы қолданғанымыздан басқа, мұнда жаңа ештеңе жоқ (интегралдың дәрежесін төмендету). Мен шешімді қысқартқанымды ескеріңіз. Тәжірибе жинақтаған сайын, интегралды ауызша табуға болады, бұл уақытты үнемдейді және тапсырмаларды орындау кезінде қолайлы. Бұл жағдайда ережені сипаттамау ұсынылады , алдымен ауызша 1-дің, содан кейін -ның интегралын аламыз.

8-мысал

Анықталмаған интегралды табыңыз.

Бұл тәуелсіз шешімге мысал, толық шешім мен жауап сабақтың соңында.

Бұл уәде етілген дәрежені арттыру:

9-мысал

Анықталмаған интегралды табыңыз.

Алдымен шешім, содан кейін түсініктемелер:

(1) Формуланы қолдану үшін интегралды дайындаңыз .

(2) Біз формуланы қолданамыз.

(3) Бөлінгішті квадраттап, интегралдық таңбадан тұрақтыны аламыз. Мұны сәл басқаша жасауға болар еді, бірақ, менің ойымша, бұл ыңғайлырақ болды.

(4) Біз формуланы қолданамыз

(5) Үшінші тоқсанда біз қайтадан дәрежені азайтамыз, бірақ формуланы қолдана отырып .

(6) Біз ұсынамыз ұқсас терминдер(мұнда мен бөлдім және толықтыруды жасады).

(7) Біз интегралды, сызықтық ережесін аламыз ал функцияны дифференциалдық таңбаға қосу әдісі ауызша орындалады.

(8) Жауапты біріктіру.

! Анықталмаған интегралда жауапты жиі бірнеше жолмен жазуға болады

Жаңа ғана қарастырылған мысалда соңғы жауап басқаша жазылуы мүмкін еді - жақшаларды ашып, тіпті өрнекті біріктіру алдында мұны істеу, яғни мысалдың келесі аяқталуы өте қолайлы:

Бұл опция одан да ыңғайлы болуы мүмкін, мен оны өзім шешуге дағдыланған жолмен түсіндірдім). Тәуелсіз шешімнің тағы бір типтік мысалы:

10-мысал

Анықталмаған интегралды табыңыз.

Бұл мысалды екі жолмен шешуге болады және сіз табысқа жетуіңіз мүмкін екі мүлдем басқа жауап(дәлірек айтқанда, олар мүлдем басқаша көрінеді, бірақ математикалық тұрғыдан олар эквивалентті болады). Сірә, сіз ең ұтымды әдісті көрмейсіз және жақшаларды ашу және басқа тригонометриялық формулаларды пайдалану арқылы зардап шегесіз. Ең тиімді шешім сабақ соңында беріледі.

Параграфты қорытындылау үшін біз қорытынды жасаймыз: пішіннің кез келген интегралы , қайда және – тіптісандар, интегралдың дәрежесін азайту әдісімен шешіледі.
Тәжірибеде мен 8 және 10 градустары бар интегралдарды кездестірдім, мен олардың қорқынышты тәртіпсіздіктерін градусты бірнеше рет төмендету арқылы шешуге тура келді, нәтижесінде ұзақ, ұзақ жауаптар болды.

Айнымалыларды ауыстыру әдісі

Мақалада айтылғандай Анықталмаған интегралдағы айнымалыны өзгерту әдісі, ауыстыру әдісін қолданудың негізгі алғышарты интегралда белгілі бір функцияның және оның туындысының болуы:
(функциялардың өнімде болуы міндетті емес)

11-мысал

Анықталмаған интегралды табыңыз.

Туындылар кестесіне қарап, формулаларды байқаймыз, , яғни біздің интегралда функция және оның туындысы бар. Алайда дифференциалдау кезінде косинус пен синус өзара бір-біріне айналатынын көреміз де, сұрақ туындайды: айнымалының өзгеруі қалай орындалады және синус немесе косинус дегенді қалай түсінеміз?! Сұрақты ғылыми ізденіс арқылы шешуге болады: егер ауыстыруды қате орындасақ, одан жақсы ештеңе шықпайды.

Жалпы нұсқаулық: ұқсас жағдайларда сіз бөлгіштегі функцияны белгілеуіңіз керек.

Біз шешімді үзіп, ауыстыруды жасаймыз

Бөлгіште бәрі жақсы, бәрі тек -ге байланысты, енді оның не болатынын білу қалады.
Ол үшін дифференциалды табамыз:

Немесе қысқаша айтқанда:
Алынған теңдіктен пропорция ережесін пайдаланып, қажетті өрнекті өрнектейміз:

Сонымен:

Енді біздің бүкіл интегралымыз тек тәуелді және біз шешуді жалғастыра аламыз

Дайын. Еске сала кетейін, ауыстырудың мақсаты интегралды жеңілдету болып табылады, бұл жағдайда бәрі кестеге сәйкес қуат функциясын біріктіруге келді;

Бұл мысалды осылайша егжей-тегжейлі сипаттағаным кездейсоқ емес, бұл сабақ материалдарын қайталау және бекіту мақсатында жасалды Анықталмаған интегралдағы айнымалыны өзгерту әдісі.

Ал енді өз шешіміңізге екі мысал:

12-мысал

Анықталмаған интегралды табыңыз.

13-мысал

Анықталмаған интегралды табыңыз.

Сабақ соңында шешімдер мен жауаптарды аяқтаңыз.

14-мысал

Анықталмаған интегралды табыңыз.

Мұнда тағы да интегралда синус пен косинус (туындысы бар функция) бар, бірақ туындыда дилемма туындайды - синус немесе косинус дегенді қалай түсінеміз?

Сіз ғылыми покинг арқылы ауыстыруды жүзеге асыруға болады, егер ештеңе жұмыс істемесе, оны басқа функция ретінде белгілеңіз, бірақ бар:

Жалпы нұсқаулық: бейнелеп айтқанда, «ыңғайсыз жағдайда» болатын функцияны белгілеу керек..

Бұл мысалда студенттік косинус дәрежеден «зардап шегетінін», ал синус еркін, өздігінен отыратынын көреміз.

Сондықтан ауыстыруды жасайық:

Егер кімде-кім айнымалыны ауыстыру және дифференциалды табу алгоритмінде әлі де қиындықтар болса, онда сіз сабаққа оралуыңыз керек. Анықталмаған интегралдағы айнымалыны өзгерту әдісі.

15-мысал

Анықталмаған интегралды табыңыз.

Интегралды талдап көрейік, немен белгілеу керек?
Нұсқауларымызды еске түсірейік:
1) функциясы азайғышта болуы ықтимал;
2) Функция "ыңғайсыз күйде".

Айтпақшы, бұл нұсқаулар тек тригонометриялық функциялар үшін ғана емес.

Синус екі критерийге де сәйкес келеді (әсіресе екінші), сондықтан ауыстыру өзін ұсынады. Негізінде, ауыстыру қазірдің өзінде жүзеге асырылуы мүмкін, бірақ алдымен не істеу керектігін анықтаған дұрыс болар еді? Алдымен біз бір косинусты «шымшып аламыз»:

Біз «болашақ» дифференциалымызды сақтаймыз

Ал біз оны синус арқылы негізгі тригонометриялық сәйкестендіру арқылы өрнектейміз:

Енді міне, ауыстыру:

Жалпы ереже: Егер интегралда тригонометриялық функциялардың бірі (синус немесе косинус) болса тақдәрежесі болса, бір функцияны тақ дәрежеден «шағып», оның артында басқа функцияны белгілеу керек.Біз тек косинустар мен синустар болатын интегралдар туралы айтып отырмыз.

Қарастырылған мысалда бізде тақ қуаттағы косинус болды, сондықтан біз қуаттан бір косинусты алып, оны синус ретінде белгіледік.

16-мысал

Анықталмаған интегралды табыңыз.

Дәрежелер көтеріліп жатыр =).
Бұл өз бетіңізше шешуге болатын мысал. Толық шешім және сабақ соңында жауап беру.

Әмбебап тригонометриялық алмастыру

Әмбебап тригонометриялық алмастыру айнымалыларды ауыстыру әдісінің кең таралған жағдайы болып табылады. Сіз оны «не істеу керектігін білмеген кезде» қолдануға болады. Бірақ іс жүзінде оны қолданудың кейбір нұсқаулары бар. Әмбебап тригонометриялық алмастыруды қолдану қажет типтік интегралдар келесі интегралдар болып табылады: , , , т.б.

17-мысал

Анықталмаған интегралды табыңыз.

Бұл жағдайда әмбебап тригонометриялық ауыстыру келесі жолмен жүзеге асырылады. ауыстырайық: . Мен әріпті пайдаланбаймын, бірақ әріп, бұл қандай да бір ереже емес, бұл жай ғана, мен қайталап айтамын, мен заттарды осылай шешуге үйрендім.

Бұл үшін теңдіктен дифференциалды табу ыңғайлырақ:
Мен екі бөлікке де арктангенс қосамын:

Арктангенс пен тангенс бірін-бірі жоққа шығарады:

Осылайша:

Іс жүзінде оны егжей-тегжейлі сипаттаудың қажеті жоқ, тек дайын нәтижені пайдаланыңыз:

! Өрнек синустар мен косинустардың астында интеграл үшін жай ғана «X» болса ғана жарамды болады. (бұл туралы кейінірек айтатын боламыз) бәрі сәл басқаша болады!

Ауыстыру кезінде синустар мен косинустар келесі бөлшектерге айналады:
, , бұл теңдіктер белгілі тригонометриялық формулаларға негізделген: ,

Сонымен, соңғы дизайн келесідей болуы мүмкін:

Әмбебап тригонометриялық ауыстыруды орындаймыз:

Сондай-ақ өз бетінше шешуге болатын тапсырмалар болады, олардың жауаптарын көруге болады.

Интегралды тригонометриялық функциялардың туындысынан қосындыға түрлендіруге болады

Интегралды х-тің бірінші дәрежелі синусы мен косинусының әр түрлі көбейткіштерге көбейтіндісі болатын интегралды, яғни түрдегі интегралды қарастырайық.

Белгілі мүмкіндіктерді пайдалану тригонометриялық формулалар

(2)
(3)
(4)
(31) түріндегі интегралдардағы туындылардың әрқайсысын алгебралық қосындыға түрлендіруге және формулалар бойынша интегралдауға болады.

(5)

(6)

1-мысал.Табу

Шешім. (2) формула бойынша сағ

2-мысал.Табу тригонометриялық функцияның интегралы

Шешім. (3) формула бойынша сағ

3-мысал.Табу тригонометриялық функцияның интегралы

Шешім. (4) формула бойынша сағ интегралдың келесі түрлендіруін аламыз:

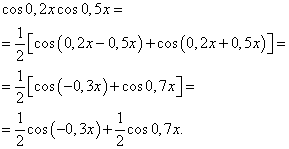
(6) формуланы қолданып, аламыз

Бір аргументтің синус пен косинус дәрежелерінің көбейтіндісінің интегралы

Енді сол аргументтің синус пен косинус дәрежелерінің туындысы болатын функциялардың интегралдарын қарастырайық, яғни.

(7)

Ерекше жағдайларда көрсеткіштердің бірі ( мнемесе n) нөл болуы мүмкін.

Мұндай функцияларды интегралдағанда косинустың жұп дәрежесін синус арқылы өрнектеуге болады, ал синус дифференциалы cos-ке тең болады. x dx(немесе тіпті синустың күшін косинус арқылы көрсетуге болады, ал косинустың дифференциалы - sinге тең x dx ) .

Екі жағдайды бөліп көрсету керек: 1) көрсеткіштердің кем дегенде біреуі мЖәне nтақ; 2) екі көрсеткіш те жұп.

Бірінші жағдай орын алсын, атап айтқанда көрсеткіш n = 2к+ 1 - тақ. Сосын, оны ескере отырып

Интеграл оның бір бөлігі тек синустың функциясы, ал екіншісі синустың дифференциалы болатындай етіп берілген. Енді айнымалы ауыстыруды пайдалану т= күнә xшешімі көпмүшені интегралдауға келтіреді т. Тек дәреже болса мтақ болса, онда олар күнә факторын оқшаулай отырып, дәл солай жасайды x, интегралдың қалған бөлігін cos арқылы өрнектейді xжәне сену т=cos x. Бұл әдісті қашан да қолдануға болады синус пен косинустың үлестік дәрежелерін біріктіру , Қашан көрсеткіштердің кем дегенде біреуі тақ . Мәселе мынада синус пен косинустың дәрежелерінің бөлімі олардың көбейтіндісінің ерекше жағдайы болып табылады : Тригонометриялық функция интегралдың бөлгішінде болғанда, оның дәрежесі теріс болады. Бірақ жартылай тригонометриялық функциялардың, олардың қуаттары тек жұп болған жағдайлары да бар. Олар туралы - келесі абзацта.

Екі көрсеткіш болса мЖәне n– жұп болса, тригонометриялық формулаларды қолдана отырып

синус пен косинустың дәрежелерін азайтыңыз, содан кейін жоғарыдағыдай типті интеграл алынады. Сондықтан интеграцияны сол схема бойынша жалғастыру керек. Егер жұп дәрежелердің бірі теріс болса, яғни синус пен косинустың жұп дәрежелерінің бөлімі қарастырылса, онда бұл схема жарамайды. . Содан кейін интегралды түрлендіруге байланысты айнымалының өзгеруі қолданылады. Мұндай жағдай келесі тармақта қарастырылады.

4-мысал.Табу тригонометриялық функцияның интегралы

Шешім. Косинус көрсеткіші тақ. Сондықтан, елестетіп көрейік

т= күнә x(Содан кейін дт=cos x dx ). Сосын аламыз

Ескі айнымалыға оралсақ, біз ақырында табамыз

5-мысал.Табу тригонометриялық функцияның интегралы

.

Шешім. Алдыңғы мысалдағыдай косинус көрсеткіші тақ, бірақ үлкенірек. Елестетіп көрейік

және айнымалыны өзгерту т= күнә x(Содан кейін дт=cos x dx ). Сосын аламыз

Жақшаларды ашайық

және аламыз

Ескі айнымалыға оралсақ, шешімді аламыз

6-мысал.Табу тригонометриялық функцияның интегралы

Шешім. Синус пен косинустың дәрежелері жұп. Сондықтан интегралдық функцияны келесідей түрлендіреміз:

Сосын аламыз

Екінші интегралда айнымалыға, параметрге өзгеріс енгіземіз т= күнә2 x. Содан кейін (1/2)дт= cos2 x dx . Демек,

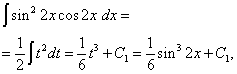
Ақыры аламыз

Айнымалыларды ауыстыру әдісін қолдану

Айнымалыларды ауыстыру әдісітригонометриялық функцияларды интегралдау кезінде оны интегралда тек синус немесе тек косинус, синусы мен косинустың көбейтіндісі болатын жағдайларда қолдануға болады, онда синус немесе косинус бірінші дәрежеде, тангенс немесе котангенс, сондай-ақ коэффициент бір аргументтің синусы мен косинусының тіпті дәрежелері. Бұл жағдайда тек күнә емес, ауыстыруды орындауға болады x = тжәне күнә x = т, сонымен қатар тг x = тжәне ctg x = т .

8-мысал.Табу тригонометриялық функцияның интегралы

.

Шешім. Айнымалыны өзгертейік: , онда . Алынған интегралды интегралдар кестесін пайдаланып оңай интегралдауға болады:

.

9-мысал.Табу тригонометриялық функцияның интегралы

Шешім. Тангенсті синус пен косинустың қатынасына түрлендірейік:

Айнымалыны өзгертейік: , онда . Алынған интеграл кесте интегралыминус белгісімен:

.

Бастапқы айнымалыға оралсақ, біз ақырында мынаны аламыз:

.

10-мысал.Табу тригонометриялық функцияның интегралы

Шешім. Айнымалыны өзгертейік: , онда .

Тригонометриялық сәйкестікті қолдану үшін интегралды түрлендірейік :

Біз интегралдың алдына минус белгісін қоюды ұмытпай, айнымалыны өзгертеміз (жоғарыдан қараңыз, неге тең дт). Содан кейін біз интегралды көбейткіштерге бөліп, кестеге сәйкес интегралдаймыз:

Бастапқы айнымалыға оралсақ, біз ақырында мынаны аламыз:

.

Тригонометриялық функцияның интегралын өзіңіз табыңыз, содан кейін шешімін қараңыз

Әмбебап тригонометриялық алмастыру

Әмбебап тригонометриялық алмастыру интеграл алдыңғы тармақтарда қарастырылған жағдайларға жатпайтын жағдайларда қолданылуы мүмкін. Негізінен, синус немесе косинус (немесе екеуі де) бөлшектің бөлгішінде болғанда. Синус пен косинусты бастапқы бұрыштың жартысының тангенсі бар басқа өрнекпен келесідей ауыстыруға болатыны дәлелденді:

Бірақ әмбебап тригонометриялық алмастыру көбінесе өте күрделі алгебралық түрлендірулерді қажет ететінін ескеріңіз, сондықтан оны басқа әдіс жұмыс істемегенде қолданған дұрыс. Әмбебап тригонометриялық алмастырумен бірге дифференциалдық таңбамен алмастыру және анықталмаған коэффициенттер әдісі қолданылатын мысалдарды қарастырайық.

12-мысал.Табу тригонометриялық функцияның интегралы

.

Шешім. Шешім. Пайдаланайық әмбебап тригонометриялық алмастыру. Содан кейін
.

Алымы мен бөлгішіндегі бөлшектерді көбейтеміз де, екеуін шығарып, бүтін таңбаның алдына қоямыз. Содан кейін

Тәжірибеде көбінесе тригонометриялық функцияларды қамтитын трансценденттік функциялардың интегралдарын есептеу қажет. Бұл материалдың бір бөлігі ретінде біз интегралдық функциялардың негізгі түрлерін сипаттаймыз және оларды біріктіру үшін қандай әдістерді қолдануға болатынын көрсетеміз.

Синус, косинус, тангенс және котангенсті интегралдау

Негізгі тригонометриялық функцияларды - sin, cos, t g, c t g интегралдау әдістерінен бастайық. Антитуындылар кестесін пайдаланып, бірден ∫ sin x d x = - cos x + C, ал ∫ cos x d x = sin x + C екенін жазамыз.

t g және c t g функцияларының анықталмаған интегралдарын есептеу үшін дифференциалдық таңбаны қолдануға болады:

∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C

Антитуындылар кестесінен алынған ∫ d x sin x = ln 1 - cos x sin x + C және ∫ d x cos x = ln 1 + sin x cos x + C формулаларын қалай алдық? Бір ғана жағдайды түсіндірейік, өйткені екіншісі ұқсастық арқылы анық болады.

Ауыстыру әдісін қолданып, жазамыз:

∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Мұнда иррационал функцияны интегралдау керек. Біз бірдей ауыстыру әдісін қолданамыз:

∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 1 - z 2 = = 1 - z ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

Енді z = 1 - t 2 және t = sin x кері ауыстыруды жасаймыз:

∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x сияқты тригонометриялық функциялардың дәрежелері бар интегралдары бар жағдайларды бөлек талдаймыз.

Оларды қалай дұрыс есептеу керектігі туралы қайталану формулаларын пайдаланып интеграция туралы мақалада оқи аласыз. Бұл формулалардың қалай шығарылатынын білсеңіз, натурал m және n болатын ∫ sin n x · cos m x d x сияқты интегралдарды оңай алуға болады.

Егер бізде тригонометриялық функциялардың көпмүшелермен немесе экспоненциалды функциялармен тіркесімі болса, онда оларды бөліктермен интегралдауға тура келеді. ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a интегралдарын табу әдістеріне арналған мақаланы оқуды ұсынамыз. · x · cos (a x) d x .

Ең қиын есептер - интегралда әртүрлі аргументтері бар тригонометриялық функцияларды қамтитын есептер. Ол үшін негізгі тригонометрия формулаларын пайдалану керек, сондықтан оларды есте сақтау немесе оларды қолмен жазып алған жөн.

1-мысал

y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) функциясының қарсы туындылар жиынын табыңыз.

Шешім

Дәрежені азайту формулаларын қолданып, cos 2 x 2 = 1 + cos x 2, cos 2 2 x = 1 + cos 4 x 2 болатынын жазайық. білдіреді,

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x · cos (3 x) + 2 · 1 + cos x 2 - 1 · sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x sin (3 x)

Бөлгіште қосындының синусының формуласы бар. Содан кейін сіз оны келесідей жаза аласыз:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)

Біз 3 интегралдың қосындысын алдық.

∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

Кейбір жағдайларда интеграл астындағы тригонометриялық функцияларды стандартты алмастыру әдісі арқылы бөлшек рационал өрнектерге келтіруге болады. Алдымен, жартылай аргументтің тангенсі арқылы sin, cos және t g мәндерін өрнектейтін формулаларды алайық:

sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2

Сонымен қатар d x дифференциалын жарты бұрыштың тангенсі арқылы өрнектеуіміз керек:

d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2 болғандықтан,

d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

Сонымен, sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x = 2 d z 1 + z 2 кезінде z = t g x 2.

2-мысал

∫ d x 2 sin x + cos x + 2 анықталмаған интегралды табыңыз.

Шешім

Біз стандартты тригонометриялық ауыстыру әдісін қолданамыз.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3

∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 болатынын аламыз.

Енді біз интегралды жай бөлшектерге кеңейтіп, екі интегралдың қосындысын аламыз:

∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = l z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Жауабы: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

Функцияларды жарты аргументтің тангенсі арқылы өрнектейтін формулалар сәйкестіктер емес екенін ескеру маңызды, сондықтан ln t g x 2 + 1 t g x 2 + 3 + C өрнек y = 1 2 функциясының қарсы туындыларының жиыны болып табылады. sin x + cos x + 2 тек анықтау облысында.

Есептердің басқа түрлерін шешу үшін негізгі интеграциялық әдістерді қолдануға болады.

Мәтінде қатені байқасаңыз, оны бөлектеп, Ctrl+Enter пернелерін басыңыз