Интеграцияның ең маңызды қасиеттері. Анықталмаған интегралдың негізгі қасиеттері
Функция болсын ж = f(x) [ интервалында анықталады а, б ], а < б. Келесі операцияларды орындайық:
1) бөлейік [ а, б] нүктелер а = x 0 < x 1 < ... < x мен- 1 < x мен < ... < x n = б қосулы nішінара сегменттер [ x 0 , x 1 ], [x 1 , x 2 ], ..., [x мен- 1 , x мен ], ..., [x n- 1 , x n ];
2) ішінара сегменттердің әрқайсысында [ x мен- 1 , x мен ], мен = 1, 2, ... n, ерікті нүктені таңдап, осы нүктедегі функцияның мәнін есептеңіз: f(z i ) ;
3) шығармаларды табыңыз f(z i ) · Δ x мен , мұндағы жартылай кесіндінің ұзындығы [ x мен- 1 , x мен ], мен = 1, 2, ... n;
4) жарасайық интегралдық қосындыфункциялары ж = f(x) сегментінде [ а, б ]:
Геометриялық тұрғыдан алғанда бұл σ қосындысы табандары жартылай кесінділер болатын тіктөртбұрыштардың аудандарының қосындысы болып табылады [ x 0 , x 1 ], [x 1 , x 2 ], ..., [x мен- 1 , x мен ], ..., [x n- 1 , x n ] және биіктіктері тең f(z 1 ) , f(z 2 ), ..., f(z n) сәйкес (Cурет 1). арқылы белгілейік λ ең ұзын жартылай сегменттің ұзындығы:
5) болғанда интегралдық қосындының шегін табыңыз λ → 0.
Анықтама.Егер интегралдық қосындының шекті шегі болса (1) және ол кесіндіні бөлу әдісіне тәуелді болмаса [ а, б] ішінара кесінділерге немесе нүктелерді таңдаудан z iоларда, онда бұл шек деп аталады анықталған интегралфункциясынан ж = f(x) сегментінде [ а, б] және белгіленеді
Осылайша,
Бұл жағдайда функция f(x) аталады интегралдықкүні [ а, б]. Сандар аЖәне бсәйкесінше интеграцияның төменгі және жоғарғы шегі деп аталады, f(x) – интегралдық функция, f(x ) dx– интегралды өрнек, x – интеграциялық айнымалы; сызық сегменті [ а, б] интегралдау интервалы деп аталады.
Теорема 1.Егер функция ж = f(x) [ интервалында үздіксіз а, б] болса, ол осы интервалда интегралданады.
Интегралдау шектері бірдей анықталған интеграл нөлге тең:
Егер а > б, содан кейін, анықтау бойынша, біз болжаймыз
2. Анықталған интегралдың геометриялық мағынасы
Сегментте болсын [ а, б] үздіксіз теріс емес функция көрсетілген ж = f(x ) . Қисық сызықты трапецияжоғарыда функцияның графигімен шектелген фигура ж = f(x), төменнен – Ox осі бойымен, солға және оңға – түзу сызықтар x = aЖәне x = b(Cурет 2).
Теріс емес функцияның анықталған интегралы ж = f(x) геометриялық тұрғыдан ауданына теңфункцияның графигімен жоғарыда шектелген қисық сызықты трапеция ж = f(x), сол және оң – сызық сегменттері x = aЖәне x = b, төменнен - Ox осінің сегменті.
3. Анықталған интегралдың негізгі қасиеттері
1. Анықталған интегралдың мәні интегралдау айнымалысының тағайындалуына тәуелді емес:
2. Анықталған интегралдың таңбасынан тұрақты көбейткішті шығаруға болады:
3. Екі функцияның алгебралық қосындысының анықталған интегралы осы функциялардың анықталған интегралдарының алгебралық қосындысына тең:
4.Егер функциясы ж = f(x) интегралданады [ а, б] Және а < б < в, Бұл
5. (орташа мән теоремасы). Егер функция ж = f(x) [ интервалында үздіксіз а, б] болса, онда бұл сегментте осындай нүкте бар
4. Ньютон-Лейбниц формуласы
2-теорема.Егер функция ж = f(x) [ интервалында үздіксіз а, б] Және Ф(x) осы сегменттегі оның антитуындыларының кез келгені болса, келесі формула жарамды:
деп аталады Ньютон-Лейбниц формуласы.Айырмашылық Ф(б) - Ф(а) әдетте келесідей жазылады:
мұндағы таңба қос қойылмалы таңба деп аталады.
Сонымен, (2) формуланы былай жазуға болады:
1-мысал.Интегралды есепте
Шешім. Интеграл үшін f(x ) = x 2 ерікті антитуындының пішіні бар
Ньютон-Лейбниц формуласында кез келген антитуындыны қолдануға болатындықтан, интегралды есептеу үшін ең қарапайым түрі бар қарсы туындыны аламыз:
5. Анықталған интегралдағы айнымалының өзгеруі
Теорема 3.Функция болсын ж = f(x) [ интервалында үздіксіз а, б]. Егер:
1) функция x = φ ( т) және оның туындысы φ "( т) үшін үздіксіз;
2) функция мәндерінің жиыны x = φ ( т) үшін бұл сегмент [ а, б ];
3) φ ( а) = а, φ ( б) = б, онда формула жарамды болады
деп аталады анықталған интегралдағы айнымалыны өзгерту формуласы .
Ұнайды анықталмаған интеграл, бұл жағдайда қажет емесбастапқы интеграциялық айнымалыға оралу үшін - α және β интеграциясының жаңа шектерін табу жеткілікті (ол үшін айнымалыны шешу керек ттеңдеулер φ ( т) = ажәне φ ( т) = б).
Ауыстырудың орнына x = φ ( т) ауыстыруды қолдануға болады т = g(x). Бұл жағдайда айнымалы бойынша интеграцияның жаңа шектерін табу тжеңілдетеді: α = g(а) , β = g(б) .
2-мысал. Интегралды есепте
Шешім. Формула арқылы жаңа айнымалы енгізейік. Теңдіктің екі жағын квадраттау арқылы 1+ аламыз x = т 2 , қайда x = т 2 - 1, dx = (т 2 - 1)"дт= 2тдт. Біз интеграцияның жаңа шегін табамыз. Ол үшін ескі шектеулерді формулаға ауыстырайық x = 3 және x = 8. Біз аламыз: , қайдан т= 2 және α = 2; , қайда т= 3 және β = 3. Сонымен,
3-мысал.Есептеңіз
Шешім. Болсын u= журнал x, Содан кейін, v = x. (4) формула бойынша
Интегралды шешу оңай тапсырма, бірақ тек таңдаулылар үшін. Бұл мақала интегралды түсінуді үйренгісі келетін, бірақ олар туралы ештеңе білмейтін немесе ештеңе білмейтіндерге арналған. Интегралдық... Ол не үшін қажет? Оны қалай есептеу керек? Анықталған және анықталмаған интегралдар дегеніміз не?
Егер сіз интеграл үшін білетін жалғыз пайдалану - жету қиын жерлерден пайдалы нәрсе алу үшін интегралды белгіше тәрізді ілмекпен тоқылған ілгекті пайдалану болса, қош келдіңіз! Ең қарапайым және басқа интегралдарды қалай шешуге болатынын және неге онсыз математикада жасай алмайтыныңызды біліңіз.
Біз тұжырымдаманы зерттейміз « ажырамас »
Интеграция бұрыннан белгілі болды Ежелгі Египет. Әрине жоқ заманауи формасы, Сонда да. Содан бері математиктер бұл тақырыпта көптеген кітаптар жазды. Әсіресе, ерекшеленді Ньютон Және Лейбниц , бірақ заттардың мәні өзгерген жоқ.
Интегралды нөлден қалай түсінуге болады? Мүмкін емес! Бұл тақырыпты түсіну үшін сізге әлі де математикалық талдау негіздері туралы негізгі білім қажет. Біздің блогта интегралды түсіну үшін қажетті ақпарат бар.
Анықталмаған интеграл
Бір функцияны алайық f(x) .
Анықталмаған интегралдық функция f(x) бұл функция деп аталады F(x) , туындысы функцияға тең f(x) .
Басқаша айтқанда, интеграл кері туынды немесе қарсы туынды болып табылады. Айтпақшы, бұл туралы біздің мақалада оқыңыз.

Антитуынды барлық үздіксіз функциялар үшін бар. Сондай-ақ антитуындыға тұрақты белгі жиі қосылады, өйткені тұрақты шамамен ерекшеленетін функциялардың туындылары сәйкес келеді. Интегралды табу процесі интегралдау деп аталады.
Қарапайым мысал:

Элементар функциялардың антитуындыларын үнемі есептемеу үшін оларды кестеге қойып, дайын мәндерді қолданған ыңғайлы.
Оқушыларға арналған интегралдардың толық кестесі

Анықталған интеграл
Интеграл түсінігімен айналысқанда біз шексіз аз шамалармен айналысамыз. Интеграл фигураның ауданын, біркелкі емес дененің массасын, біркелкі емес қозғалыс кезінде жүріп өткен қашықтықты және т.б. есептеуге көмектеседі. Интеграл шексіз қосынды екенін есте ұстаған жөн үлкен мөлшершексіз аз мүшелер.
Мысал ретінде қандай да бір функцияның графигін елестетіңіз.

Функция графигімен шектелген фигураның ауданын қалай табуға болады? Интегралды қолдану! Координаталық осьтермен және функцияның графигімен шектелген қисық сызықты трапецияны шексіз аз кесінділерге бөлейік. Осылайша фигура жұқа бағандарға бөлінеді. Бағандардың аудандарының қосындысы трапецияның ауданы болады. Бірақ мұндай есептеу шамамен нәтиже беретінін есте сақтаңыз. Дегенмен, сегменттер неғұрлым аз және тар болса, соғұрлым есептеу дәлірек болады. Егер біз оларды ұзындығы нөлге бейім болатындай дәрежеде азайтсақ, онда сегменттер аудандарының қосындысы фигураның ауданына бейім болады. Бұл белгілі бір интеграл, ол былай жазылады:

a және b нүктелері интегралдау шегі деп аталады.

« Ажырамас »
Айтпақшы! Біздің оқырмандар үшін қазір 10% жеңілдік бар
Манекендер үшін интегралды есептеу ережелері
Анықталмаған интегралдың қасиеттері
Анықталмаған интеграл қалай шешіледі? Мұнда мысалдарды шешу кезінде пайдалы болатын анықталмаған интегралдың қасиеттерін қарастырамыз.
- Интегралдың туындысы интегралға тең:

- Тұрақтыны интегралдық таңбаның астынан шығаруға болады:

- Қосындының интегралы интегралдардың қосындысына тең. Бұл айырмашылыққа да қатысты:
Анықталған интегралдың қасиеттері
- Сызықтық:

- Интегралдың таңбасы өзгереді, егер интегралдау шегі ауыстырылса:

- Сағат кез келгенұпай а, бЖәне бірге:

Анықталған интеграл қосындының шегі екенін біз бұрыннан анықтадық. Бірақ мысалды шешу кезінде нақты мәнді қалай алуға болады? Бұл үшін Ньютон-Лейбниц формуласы бар:

Интегралды шешу мысалдары
Төменде анықталмаған интегралды және шешімдері бар мысалдарды қарастырамыз. Біз сізге шешімнің қыр-сырын өзіңіз анықтауды ұсынамыз, егер бірдеңе түсініксіз болса, түсініктемелерде сұрақтар қойыңыз.

Материалды бекіту үшін интегралдар тәжірибеде қалай шешілетіні туралы бейнероликті қараңыз. Егер интеграл бірден берілмесе, үмітіңізді үзбеңіз. Студенттерге арналған кәсіби қызметке хабарласыңыз және жабық беттегі кез келген үштік немесе қисық интеграл сіздің күшіңізде болады.
Бұл қасиеттер интегралды элементар интегралдардың біріне келтіру және одан әрі есептеу мақсатында түрлендірулерді жүзеге асыру үшін қолданылады.
1. Анықталмаған интегралдың туындысы интегралға тең:
2. Анықталмаған интегралдың дифференциалы интегралға тең:
3. Белгілі бір функцияның дифференциалының анықталмаған интегралы осы функция мен ерікті тұрақтының қосындысына тең:
4. Тұрақты коэффициентті интегралдық таңбадан шығаруға болады:
Сонымен қатар, a ≠ 0
5. Қосындының (айырымның) интегралы интегралдардың қосындысына (айырымы) тең:
6. Меншік 4 және 5 қасиеттердің қосындысы:
Сонымен қатар, a ≠ 0 ˄ b ≠ 0
7. Анықталмаған интегралдың инварианттық қасиеті:
Егер болса, онда
8. Мүлік:
Егер болса, онда
Шын мәнінде, бұл қасиет келесі бөлімде толығырақ қарастырылатын айнымалыны өзгерту әдісін қолданатын интеграцияның ерекше жағдайы болып табылады.
Мысал қарастырайық:
Алдымен 5-қасиетті, содан кейін 4-қасиетті қолдандық, содан кейін антитуындылар кестесін қолданып, нәтиже алдық.
Біздің онлайн интегралдық калькулятордың алгоритмі жоғарыда аталған барлық қасиеттерді қолдайды және сіздің интегралыңыздың егжей-тегжейлі шешімін оңай табады.
Бұл мақалада анықталған интегралдың негізгі қасиеттері туралы егжей-тегжейлі айтылады. Олар Риман және Дарбу интегралы тұжырымдамасы арқылы дәлелденді. Анықталған интегралды есептеу 5 қасиетінің арқасында жүзеге асады. Қалғандары әртүрлі өрнектерді бағалау үшін қолданылады.
Анықталған интегралдың негізгі қасиеттеріне көшпес бұрын, а-дан b аспайтынына көз жеткізу керек.
Анықталған интегралдың негізгі қасиеттері
Анықтама 1x = a нүктесінде анықталған y = f (x) функциясы ∫ a a f (x) d x = 0 әділ теңдігіне ұқсас.
Дәлел 1
Бұдан шекаралары сәйкес келетін интегралдың мәні нөлге тең екенін көреміз. Бұл Риман интегралының салдары, өйткені [ a аралықтағы кез келген бөлім үшін әрбір интегралдық қосынды σ; a ] және ζ i нүктелерінің кез келген таңдауы нөлге тең, өйткені x i - x i - 1 = 0 , i = 1 , 2 , . . . , n , яғни интегралдық функциялардың шегі нөлге тең екенін табамыз.
Анықтама 2
[a интервалында интегралданатын функция үшін; b ] , ∫ a b f (x) d x = - ∫ b a f (x) d x шарты орындалады.
Дәлел 2
Басқаша айтқанда, егер интеграцияның жоғарғы және төменгі шекараларын ауыстырсаңыз, интегралдың мәні қарама-қарсы мәнге өзгереді. Бұл мүлікРиман интегралынан алынған. Дегенмен, кесіндінің бөлімін нөмірлеу x = b нүктесінен басталады.
Анықтама 3
∫ a b f x ± g (x) d x = ∫ a b f (x) d x ± ∫ a b g (x) d x [ a аралықта анықталған y = f (x) және y = g (x) типті интегралданатын функцияларға қолданылады; b].
Дәлел 3
ζ i нүктелерінің берілген таңдауы бар кесінділерге бөлу үшін y = f (x) ± g (x) функциясының интегралдық қосындысын жазыңыз: σ = ∑ i = 1 n f ζ i ± g ζ i · x i - x i - 1 = = ∑ i = 1 n f (ζ i) · x i - x i - 1 ± ∑ i = 1 n g ζ i · x i - x i - 1 = σ f ± σ g
Мұндағы σ f және σ g - сегментті бөлуге арналған y = f (x) және y = g (x) функцияларының интегралдық қосындылары. λ = m a x i = 1, 2, кезіндегі шекке өткеннен кейін. . . , n (x i - x i - 1) → 0 lim λ → 0 σ = lim λ → 0 σ f ± σ g = lim λ → 0 σ g ± lim λ → 0 σ g болатынын аламыз.
Риманның анықтамасынан бұл өрнек эквивалентті.
Анықтама 4
Тұрақты көбейткішті анықталған интеграл таңбасынан тыс кеңейту. [a] аралығынан интегралды функция; b ] ерікті мәнімен k ∫ a b k · f (x) d x = k · ∫ a b f (x) d x түріндегі әділ теңсіздікке ие.
Дәлелдеу 4
Белгілі бір интегралдық меншіктің дәлелі алдыңғыға ұқсас:
σ = ∑ i = 1 n k · f ζ i · (x i - x i - 1) = = k · ∑ i = 1 n f ζ i · (x i - x i - 1) = k · σ f ⇒ lim λ → 0 σ = lim λ → 0 (k · σ f) = k · lim λ → 0 σ f ⇒ ∫ a b k · f (x) d x = k · ∫ a b f (x) d x
Анықтама 5
Егер y = f (x) түріндегі функция ∈ x, b ∈ x интервалында интегралданатын болса, ∫ a b f (x) d x = ∫ a c f (x) d x + ∫ c b f (x) d болатынын аламыз. x.
Дәлел 5
Мүлік c ∈ a үшін жарамды болып саналады; b, c ≤ a және c ≥ b үшін. Дәлелдеу алдыңғы қасиеттерге ұқсас.
Анықтама 6
Функция сегментінен интегралдауға болатын кезде [a; b ], онда бұл кез келген ішкі c сегменті үшін мүмкін болады; d ∈ a ; б.
Дәлелдеу 6
Дәлелдеу Darboux қасиетіне негізделген: егер нүктелер сегменттің бар бөліміне қосылса, онда төменгі Darboux қосындысы азаймайды, ал жоғарғысы өспейді.
Анықтама 7
Функция [a; b ] бастап f (x) ≥ 0 f (x) ≤ 0 кез келген x ∈ a мәні үшін; b , онда ∫ a b f (x) d x ≥ 0 ∫ a b f (x) ≤ 0 болатынын аламыз.
Қасиетті Риман интегралының анықтамасы арқылы дәлелдеуге болады: f (x) ≥ 0 f (x) ≤ 0 теріс емес деген шартпен кесіндінің бөліну нүктелерінің және ζ i нүктелерінің кез келген таңдауы үшін кез келген интегралдық қосынды. .
Дәлелдер 7
Егер y = f (x) және y = g (x) функциялары [ a аралықта интегралданатын болса; b ] болса, келесі теңсіздіктер дұрыс деп саналады:
∫ a b f (x) d x ≤ ∫ a b g (x) d x , f (x) ≤ g (x) ∀ x ∈ a ; b ∫ a b f (x) d x ≥ ∫ a b g (x) d x , f (x) ≥ g (x) ∀ x ∈ a ; б
Мәлімдеменің арқасында біз интеграцияның рұқсат етілгенін білеміз. Бұл қорытынды басқа қасиеттерді дәлелдеу үшін пайдаланылады.
Анықтама 8
Интегралданатын функция үшін y = f (x) аралығынан [ a ; b ] бізде ∫ a b f (x) d x ≤ ∫ a b f (x) d x түріндегі әділ теңсіздік бар.
Дәлелдеу 8
Бізде бұл - f (x) ≤ f (x) ≤ f (x) . Алдыңғы қасиеттен біз теңсіздікті мүшелер бойынша интегралдауға болатынын анықтадық және ол - ∫ a b f (x) d x ≤ ∫ a b f (x) d x ≤ ∫ a b f (x) d x түріндегі теңсіздікке сәйкес келеді. Бұл қос теңсіздікті басқа түрде жазуға болады: ∫ a b f (x) d x ≤ ∫ a b f (x) d x .
Анықтама 9
y = f (x) және y = g (x) функциялары [ a интервалынан интегралдағанда; b ] кез келген x ∈ a үшін g (x) ≥ 0 ; b , m · ∫ a b g (x) d x ≤ ∫ a b f (x) · g (x) d x ≤ M · ∫ a b g (x) d x түріндегі теңсіздікті аламыз, мұндағы m = m i n x ∈ a ; b f (x) және M = m a x x ∈ a ; b f (x) .
Дәлел 9
Дәлелдеу дәл осылай жүзеге асырылады. M және m [a кесіндісінен анықталған y = f (x) функциясының ең үлкен және ең кіші мәндері болып саналады; b ] , содан кейін m ≤ f (x) ≤ M . Қос теңсіздікті y = g (x) функциясына көбейту керек, ол m g (x) ≤ f (x) g (x) ≤ M g (x) түріндегі қос теңсіздіктің мәнін береді. Оны [a интервалына біріктіру керек; b ] болса, онда дәлелденетін тұжырымды аламыз.
Салдары: g (x) = 1 үшін теңсіздік m · b - a ≤ ∫ a b f (x) d x ≤ M · (b - a) түрін алады.
Бірінші орташа формула
Анықтама 10y = f (x) үшін [ a интервалында интегралданатын ; b ] m = m i n x ∈ a болғанда; b f (x) және M = m a x x ∈ a ; b f (x) μ ∈ m саны бар; M , ол ∫ a b f (x) d x = μ · b - a сәйкес келеді.
Салдары: y = f (x) функциясы [ a интервалынан үзіліссіз болғанда ; b ] болса, онда c ∈ a саны болады; b, теңдігін қанағаттандыратын ∫ a b f (x) d x = f (c) b - a.
Жалпылама түрдегі бірінші орташа формула
Анықтама 11y = f (x) және y = g (x) функциялары [ a интервалынан интегралданатын болғанда; b ] m = m i n x ∈ a болғанда; b f (x) және M = m a x x ∈ a ; b f (x) , және кез келген x ∈ a мәні үшін g (x) > 0 ; б. Осыдан μ ∈ m саны бар екенін аламыз; ∫ a b f (x) · g (x) d x = μ · ∫ a b g (x) d x теңдігін қанағаттандыратын M .
Екінші орташа формула
Анықтама 12y = f (x) функциясы [ a интервалынан интегралданатын болғанда; b ], ал y = g (x) монотонды болса, онда c ∈ a болатын сан бар; b , мұнда ∫ a b f (x) · g (x) d x = g (a) · ∫ a c f (x) d x + g (b) · ∫ c b f (x) d x түріндегі әділ теңдікті аламыз.
Мәтінде қатені байқасаңыз, оны бөлектеп, Ctrl+Enter пернелерін басыңыз
Антитуынды функция және анықталмаған интеграл
1-факт. Интеграция - дифференциалдаудың кері әрекеті, атап айтқанда, функцияны осы функцияның белгілі туындысынан қалпына келтіру. Осылайша функция қалпына келтірілді Ф(x) аталады антитуындыфункциясы үшін f(x).
Анықтама 1. Функция Ф(x f(x) белгілі бір аралықта X, егер барлық мәндер үшін xосы аралықтан бастап теңдік сақталады Ф "(x)=f(x), яғни бұл функция f(x) антитуынды функцияның туындысы болып табылады Ф(x). .
Мысалы, функция Ф(x) = күнә x функцияның антитуындысы болып табылады f(x) = cos x бүкіл сандар жолында, өйткені кез келген х мәні үшін (күнә x)" = (кос x) .
Анықтама 2. Функцияның анықталмаған интегралы f(x) оның барлық антитуындыларының жиынтығы. Бұл жағдайда белгі қолданылады
∫
f(x)dx
,белгісі қайда ∫ интегралдық таңба, функция деп аталады f(x) – интегралдық функция, және f(x)dx – интегралды өрнек.
Осылайша, егер Ф(x) – кейбір антитуынды f(x), Бұл
∫
f(x)dx = Ф(x) +C
Қайда C - ерікті тұрақты (тұрақты).
Анықталмаған интеграл ретіндегі функцияның антитуындылар жиынының мағынасын түсіну үшін келесі ұқсастық орынды болады. Есік болсын (дәстүрлі ағаш есік). Оның қызметі – «есік болу». Есік неден жасалған? Ағаштан жасалған. Бұл «есік болу» функциясының интегралының антитуындыларының жиыны, яғни оның анықталмаған интегралы «ағаш болу + С» функциясы екенін білдіреді, мұндағы С тұрақты, осы контексте мүмкін болатын мысалы, ағаштың түрін білдіреді. Есік кейбір құралдарды пайдаланып ағаштан жасалғаны сияқты, функцияның туындысы антитуынды функциядан «жасалады». туындыны оқу барысында біз үйренген формулалар .
Сонда жалпы объектілердің және оларға сәйкес келетін антитуындылардың функцияларының кестесі («есік болу» - «ағаш», «қасық болу» - «металл болу» т.б.) негізгі кестеге ұқсас. анықталмаған интегралдар, олар төменде келтіріледі. Анықталмаған интегралдар кестесі осы функциялар «жасалатын» антитуындыларды көрсете отырып, жалпы функцияларды тізімдейді. Анықталмаған интегралды табуға берілген есептердің бір бөлігінде көп күш жұмсамай тікелей интегралдауға болатын, яғни анықталмаған интегралдар кестесін пайдалана отырып, интегралдар берілген. Күрделі есептерде кесте интегралдарын қолдануға болатындай етіп алдымен интегралды түрлендіру керек.
2-факт. Антитуынды ретінде функцияны қалпына келтіргенде ерікті тұрақтыны (тұрақты) ескеру керек. C, ал 1-ден шексіздікке дейінгі әртүрлі тұрақтылары бар антитуындылар тізімін жазбау үшін ерікті тұрақтысы бар антитуындылар жиынын жазу керек. C, мысалы, келесідей: 5 x³+C. Сонымен, антитуынды өрнекке ерікті тұрақты (тұрақты) кіреді, өйткені антитуынды функция бола алады, мысалы, 5 x³+4 немесе 5 x³+3 және дифференциалданғанда 4 немесе 3 немесе кез келген басқа тұрақты нөлге айналады.
Интегралдау мәселесін қояйық: бұл функция үшін f(x) мұндай функцияны табыңыз Ф(x), кімнің туындысытең f(x).
1-мысал.Функцияның антитуындылар жиынын табыңыз
Шешім. Бұл функция үшін антитуынды функция болып табылады
Функция Ф(x) функциясына қарсы туынды деп аталады f(x), туынды болса Ф(x) тең f(x), немесе, бұл бірдей нәрсе, дифференциал Ф(x) тең f(x) dx, яғни.
![]() (2)
(2)
Демек, функция функцияның антитуындысы болып табылады. Дегенмен, ол үшін жалғыз антидериватив емес. Олар сондай-ақ функция қызметін атқарады
Қайда МЕН– ерікті тұрақты. Мұны дифференциация арқылы тексеруге болады.
Сонымен, егер функция үшін бір антитуынды болса, онда ол үшін тұрақты мүшемен ерекшеленетін антитуындылардың шексіз саны болады. Функцияның барлық қарсы туындылары жоғарыда келтірілген түрде жазылған. Бұл келесі теоремадан туындайды.
Теорема (2 фактінің ресми мәлімдемесі).Егер Ф(x) – функцияға қарсы туынды f(x) белгілі бір аралықта X, содан кейін кез келген басқа антитуынды f(x) бірдей интервалда түрінде ұсынылуы мүмкін Ф(x) + C, Қайда МЕН– ерікті тұрақты.
Келесі мысалда анықталмаған интегралдың қасиеттерінен кейін 3-тармақта берілетін интегралдар кестесіне жүгінеміз. Жоғарыда айтылғандардың мәні түсінікті болу үшін біз мұны бүкіл кестені оқымас бұрын жасаймыз. Ал кесте мен қасиеттерден кейін интеграция кезінде оларды толықтай қолданамыз.
2-мысал.Антитуынды функциялардың жиынын табыңыз:
Шешім. Біз бұл функциялар «жасалатын» антитуынды функциялардың жиынын табамыз. Интегралдар кестесіндегі формулаларды айтқан кезде, әзірге ондай формулалар бар екенін қабылдаңыз, біз анықталмаған интегралдар кестесінің өзін одан әрі зерттейміз.
1) үшін интегралдар кестесінен (7) формуланы қолдану n= 3, аламыз
![]()
2) үшін интегралдар кестесіндегі (10) формуланы қолдану n= 1/3, бізде бар
3) бері
содан кейін (7) формулаға сәйкес n= -1/4 табамыз
![]()
Интегралдық таңбаның астында жазылатын функцияның өзі емес. f, және оның дифференциал бойынша туындысы dx. Бұл, ең алдымен, антитуынды қай айнымалы арқылы ізделетінін көрсету үшін жасалады. Мысалы,
![]() ,
,
![]() ;
;
мұнда екі жағдайда да интеграл тең, бірақ қарастырылған жағдайларда оның анықталмаған интегралдары басқа болып шығады. Бірінші жағдайда бұл функция айнымалының функциясы ретінде қарастырылады x, ал екіншісінде - функциясы ретінде z .
Функцияның анықталмаған интегралын табу процесі сол функцияны интегралдау деп аталады.
Анықталмаған интегралдың геометриялық мағынасы
Бізге қисық сызықты табу керек делік y=F(x)және оның әрбір нүктесіндегі жанама бұрыштың тангенсі берілген функция екенін біз бұрыннан білеміз f(x)осы нүктенің абсциссасы.
Туындының геометриялық мағынасына сәйкес қисық сызықтың берілген нүктесіндегі жанаманың көлбеу бұрышының тангенсі y=F(x)туындының мәніне тең F"(x). Сондықтан мұндай функцияны табу керек F(x), ол үшін F"(x)=f(x). Тапсырмада қажет функция F(x)-ның антитуындысы болып табылады f(x). Есептің шарттарын бір қисық емес, қисықтардың тобы қанағаттандырады. y=F(x)- осы қисықтардың біреуін, ал кез келген басқа қисықты одан ось бойымен параллель аудару арқылы алуға болады Ой.
-ның антитуынды функциясының графигін шақырайық f(x)интегралдық қисық. Егер F"(x)=f(x), содан кейін функцияның графигі y=F(x)интегралдық қисық бар.
3-факт. Анықталмаған интеграл геометриялық түрде барлық интегралдық қисықтардың тобымен берілген , төмендегі суреттегідей. Әрбір қисықтың координаталар басынан қашықтығы ерікті интегралдау константасы арқылы анықталады C.

Анықталмаған интегралдың қасиеттері
4-факт. Теорема 1. Анықталмаған интегралдың туындысы интегралға тең, ал дифференциалы интегралға тең.
5-факт. Теорема 2. Функция дифференциалының анықталмаған интегралы f(x) функциясына тең f(x) тұрақты мерзімге дейін , яғни.
![]() (3)
(3)
1 және 2 теоремалар дифференциалдау мен интегралдау өзара кері амалдар екенін көрсетеді.
6-факт. Теорема 3. Интегралдағы тұрақты факторды анықталмаған интегралдың таңбасынан шығаруға болады. , яғни.
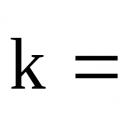 Реакция жылдамдығының тұрақтысы Зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар
Реакция жылдамдығының тұрақтысы Зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар Өлгеннен кейін өмір бар ма?
Өлгеннен кейін өмір бар ма? Ғалымдар: Жер – адамзат ғалымдары үшін «ғарыштық түрме»: Жер – ғаламдағы ғарыш түрмесі
Ғалымдар: Жер – адамзат ғалымдары үшін «ғарыштық түрме»: Жер – ғаламдағы ғарыш түрмесі