احتمال سقوط یک متغیر تصادفی در یک بازه آنلاین. قانون توزیع عادی
بیایید تابع توزیع را پیدا کنیم متغیر تصادفی ایکس، تابع قانون عادیتوزیع ها:
بیایید تغییری در انتگرال ایجاد کنیم و آن را به شکل بیاوریم:
 .
.
انتگرال  از طریق توابع ابتدایی بیان نمی شود، اما می توان آن را از طریق یک تابع خاص محاسبه کرد انتگرال معیناز بیان یا . بیایید تابع را بیان کنیم
از طریق توابع ابتدایی بیان نمی شود، اما می توان آن را از طریق یک تابع خاص محاسبه کرد انتگرال معیناز بیان یا . بیایید تابع را بیان کنیم  از طریق تابع لاپلاس Ф(х):
از طریق تابع لاپلاس Ф(х):
 .
.
احتمال سقوط یک متغیر تصادفی X در ناحیه (α، β) با فرمول بیان می شود:
 .
.
با استفاده از آخرین فرمول می توان احتمال انحراف یک متغیر تصادفی نرمال از آن را تخمین زد انتظارات ریاضیبه یک مقدار مثبت دلخواه کوچک ε از پیش تعیین شده:
 .
.
بگذار پس و . در تی=3 دریافت می کنیم، یعنی. این رویداد که انحراف یک متغیر تصادفی توزیع شده نرمال از انتظارات ریاضی کمتر باشد عملاً قطعی است.
این هست قانون سه سیگما: اگر یک متغیر تصادفی به طور نرمال توزیع شود، قدر مطلق انحراف مقادیر آن از انتظارات ریاضی از سه برابر انحراف استاندارد تجاوز نمی کند.
وظیفه.اجازه دهید قطر قطعه تولید شده توسط کارگاه یک متغیر تصادفی باشد که به طور معمول توزیع شده است. m = 4.5 سانتیمتر، سانتیمتر احتمال اینکه قطر قطعهای که بهطور تصادفی گرفته شده است با انتظارات ریاضی آن بیش از 1 میلیمتر تفاوت نداشته باشد را بیابید.
راه حل. این مشکل با مقادیر زیر پارامترهایی که احتمال مورد نظر را تعیین می کنند مشخص می شود:  ، F(0.2)=0.0793،
، F(0.2)=0.0793،
کنترل سوالات
1. کدام توزیع احتمال یکنواخت نامیده می شود؟
2. تابع توزیع یک متغیر تصادفی که به طور یکنواخت در بازه [ آ؛ ب]?
3. چگونه می توان احتمال مقادیر یک متغیر تصادفی توزیع شده یکنواخت در یک بازه معین را محاسبه کرد؟
4- توزیع نمایی یک متغیر تصادفی چگونه تعیین می شود؟
5. تابع توزیع یک متغیر تصادفی که طبق قانون نمایی توزیع شده است چه شکلی دارد؟
6. به کدام توزیع احتمال نرمال می گویند؟
7. چگالی توزیع نرمال چه ویژگی هایی دارد؟ چگونه پارامترهای توزیع نرمال بر ظاهر نمودار چگالی توزیع نرمال تأثیر می گذارد؟
8. چگونه می توان احتمال مقادیر یک متغیر تصادفی توزیع شده معمولی در یک بازه معین را محاسبه کرد؟
9. چگونه می توان احتمال انحراف مقادیر یک متغیر تصادفی با توزیع نرمال را از انتظارات ریاضی آن محاسبه کرد؟
10. قانون «سه سیگما» را فرموله کنید؟
11. انتظارات ریاضی، پراکندگی و انحراف معیار یک متغیر تصادفی توزیع شده بر اساس قانون یکنواخت در بخش [ آ؛ ب]?
12. انتظارات ریاضی، واریانس و انحراف معیار یک متغیر تصادفی توزیع شده بر اساس قانون نمایی با پارامتر λ چیست؟
13. انتظارات ریاضی، واریانس و انحراف معیار یک متغیر تصادفی توزیع شده بر اساس یک قانون نرمال با پارامترها چیست؟ مترو
1. متغیر تصادفی ایکسبه طور یکنواخت در بازه [-3، 5] توزیع شده است. چگالی توزیع و تابع توزیع را پیدا کنید ایکس. نمودارهای هر دو تابع را بسازید. احتمالات و . مقدار مورد انتظار، واریانس و انحراف معیار را محاسبه کنید ایکس.
2. اتوبوس های مسیر شماره 21 به طور منظم در فواصل 10 دقیقه حرکت می کنند. مسافری در یک توقف در زمان تصادفی پیاده می شود. یک متغیر تصادفی را در نظر بگیرید ایکس- زمان انتظار مسافر برای اتوبوس (در چند دقیقه). چگالی توزیع و تابع توزیع را پیدا کنید ایکس. نمودارهای هر دو تابع را بسازید. این احتمال را پیدا کنید که یک مسافر نباید بیش از پنج دقیقه منتظر اتوبوس بماند. میانگین زمان انتظار اتوبوس و واریانس زمان انتظار اتوبوس را بیابید.
3. ثابت شده است که زمان تعمیر برای یک VCR (به روز) یک متغیر تصادفی است ایکس، بر اساس قانون نمایی توزیع شده است. میانگین زمان تعمیر یک VCR 10 روز است. چگالی توزیع و تابع توزیع را پیدا کنید ایکس. نمودارهای هر دو تابع را بسازید. احتمال اینکه تعمیر VCR حداقل 11 روز طول بکشد را پیدا کنید.
4. نمودارهای چگالی و توابع توزیع یک متغیر تصادفی را رسم کنید ایکس، طبق قانون عادی با پارامترها توزیع می شود متر= = - 2 و = 0.2.
فرم های مشخص کردن قانون توزیع برای متغیرهای تصادفی پیوسته
اشکال تنظیم قانون توزیع متغیرهای تصادفی گسسته
1). جدول توزیع (ردیف) - ساده ترین شکل تعیین قانون توزیع متغیرهای تصادفی گسسته.
از آنجایی که جدول تمام مقادیر ممکن متغیر تصادفی را فهرست می کند.
2). چند ضلعی توزیع . در نمایش گرافیکیسری های توزیع در یک سیستم مختصات مستطیلی، تمام مقادیر ممکن متغیر تصادفی در امتداد محور آبسیسا و احتمالات مربوط به آنها در امتداد محور مختصات رسم می شوند. سپس نقاط ترسیم شده و با قطعات مستقیم به هم متصل می شوند. شکل حاصل - یک چند ضلعی توزیع - نیز شکلی از تعیین قانون توزیع یک متغیر تصادفی گسسته است.
3). تابع توزیع - احتمال اینکه یک متغیر تصادفی X مقداری کمتر از مقدار x داده شده را بگیرد، یعنی
| . |
از نظر هندسی می توان آن را احتمال برخورد با یک نقطه تصادفی در نظر گرفت ایکسبه بخشی از محور اعداد که در سمت چپ یک نقطه ثابت قرار دارد ایکس.
2) ; ;
وظیفه 2.1.مقدار تصادفی ایکس- تعداد ضربه به هدف با 3 شلیک (مشکل 1.5 را ببینید). یک سری توزیع، یک چندضلعی توزیع بسازید، مقادیر تابع توزیع را محاسبه کنید و نمودار آن را بسازید.
راه حل:
1) سری توزیع یک متغیر تصادفی ایکسدر جدول ارائه شده است
| در | , |
| در | , |
| در | , |
| در | |
| در | . |
رسم مقادیر روی محور آبسیسا ایکس،و در امتداد محور ارتین - مقادیر و با انتخاب یک مقیاس معین، نموداری از تابع توزیع به دست می آوریم (شکل 2.2). تابع توزیع یک متغیر تصادفی گسسته دارای جهش (ناپیوستگی) در نقاطی است که در آن متغیر تصادفی ایکسمقادیر خاص مشخص شده در جدول توزیع را می گیرد. مجموع تمام جهش ها در تابع توزیع برابر با یک است.
برنج. 2.2 - تابع توزیع یک مقدار گسسته
1). تابع توزیع .
برای یک متغیر تصادفی پیوسته، نمودار تابع توزیع (شکل 2.3) شکل یک منحنی صاف دارد.
ویژگی های تابع توزیع:
ج) اگر .
برنج. 2.3 - تابع توزیع مقدار پیوسته
2). چگالی توزیع که تعریف میشود مشتق تابع توزیع، یعنی.
| . |
منحنی که چگالی توزیع یک متغیر تصادفی را نشان می دهد، تماس گرفت منحنی توزیع (شکل 2.4).
خواص چگالی:
و آنها. چگالی یک تابع غیر منفی است.
ب) یعنی منطقه محدود منحنی توزیع و محور x همیشه برابر با 1 است.
اگر تمام مقادیر ممکن یک متغیر تصادفی باشد ایکسمحدوده از آقبل از ب، سپس خاصیت دوم چگالی به شکل زیر در می آید:
برنج. 2.4 - منحنی توزیع
در عمل، اغلب لازم است که احتمال یک متغیر تصادفی را بدانیم ایکسمقداری را در محدوده ای، به عنوان مثال، از a تا b می گیرد. احتمال لازم برای متغیر تصادفی گسسته ایکسبا فرمول تعیین می شود
از آنجایی که احتمال هر مقدار فردی یک متغیر تصادفی پیوسته صفر است: .
احتمال ضربه زدن به یک متغیر تصادفی پیوسته ایکسبه فاصله (a,b) نیز با عبارت:
مشکل 2.3.مقدار تصادفی ایکستوسط تابع توزیع داده می شود
چگالی و همچنین احتمال اینکه نتیجه آزمون یک متغیر تصادفی باشد را بیابید ایکسمقدار موجود در بازه را می گیرد.
راه حل:
2. احتمال ضربه زدن به یک متغیر تصادفی ایکسدر فاصله با فرمول تعیین می شود. گرفتن و، پیدا می کنیم
در بسیاری از مسائل مربوط به متغیرهای تصادفی با توزیع نرمال، لازم است که احتمال سقوط یک متغیر تصادفی، تابع یک قانون نرمال با پارامترها، بر روی بخش از تا تعیین شود. برای محاسبه این احتمال از فرمول کلی استفاده می کنیم
تابع توزیع کمیت کجاست.
بیایید تابع توزیع یک متغیر تصادفی را که طبق یک قانون عادی با پارامترها توزیع شده است، پیدا کنیم. چگالی توزیع مقدار برابر است با:
 .
(6.3.2)
.
(6.3.2)
از اینجا تابع توزیع را پیدا می کنیم
 . (6.3.3)
. (6.3.3)
اجازه دهید تغییری در متغیر در انتگرال ایجاد کنیم (6.3.3)
و بیایید آن را به این شکل قرار دهیم:
 (6.3.4)
(6.3.4)
انتگرال (6.3.4) از طریق توابع ابتدایی بیان نمی شود، اما می توان آن را از طریق یک تابع خاص که انتگرال معینی از عبارت را بیان می کند یا (به اصطلاح انتگرال احتمال) محاسبه کرد که جداول برای آن جمع آوری شده است. انواع مختلفی از این توابع وجود دارد، به عنوان مثال:
 ;
;

و غیره. استفاده از کدام یک از این عملکردها سلیقه ای است. ما به عنوان چنین تابعی را انتخاب خواهیم کرد
 . (6.3.5)
. (6.3.5)
به راحتی می توان فهمید که این تابع چیزی بیش از یک تابع توزیع برای یک متغیر تصادفی توزیع شده معمولی با پارامترها نیست.
اجازه دهید موافقت کنیم که تابع را تابع توزیع عادی بنامیم. پیوست (جدول 1) شامل جداول مقادیر تابع است.
اجازه دهید تابع توزیع (6.3.3) کمیت را با پارامترها و از طریق تابع توزیع نرمال بیان کنیم. به طور مشخص،
![]() .
(6.3.6)
.
(6.3.6)
حالا بیایید احتمال سقوط یک متغیر تصادفی در بخش از تا را پیدا کنیم. طبق فرمول (6.3.1)
بنابراین، ما احتمال توزیع یک متغیر تصادفی بر اساس یک قانون نرمال را با هر پارامتری از طریق تابع توزیع استاندارد مربوط به ساده ترین قانون نرمال با پارامترهای 0.1 به یک بخش بیان کردیم. توجه داشته باشید که آرگومان های تابع در فرمول (6.3.7) معنای بسیار ساده ای دارند: فاصله انتهای سمت راست بخش تا مرکز پراکندگی وجود دارد که در انحرافات استاندارد بیان می شود. - همان فاصله برای انتهای سمت چپ مقطع، و اگر انتهای آن در سمت راست مرکز پراکندگی قرار گیرد، این فاصله مثبت و اگر به سمت چپ باشد منفی در نظر گرفته می شود.
مانند هر تابع توزیع، تابع دارای ویژگی های زیر است:
3. - عملکرد غیر کاهشی.
علاوه بر این، از تقارن توزیع نرمال با پارامترهای نسبت به مبدا، نتیجه میشود که
با استفاده از این ویژگی، به بیان دقیق، می توان جداول تابع را فقط به مقادیر آرگومان مثبت محدود کرد، اما برای جلوگیری از عملیات غیر ضروری (تفریق از یک)، جدول ضمیمه 1 مقادیری را برای آرگومان های مثبت و منفی ارائه می دهد.

در عمل، ما اغلب با مشکل محاسبه احتمال سقوط یک متغیر تصادفی با توزیع نرمال در ناحیه ای مواجه می شویم که نسبت به مرکز پراکندگی متقارن است. بیایید چنین مقطعی از طول را در نظر بگیریم (شکل 6.3.1). بیایید با استفاده از فرمول (6.3.7) احتمال برخورد با این ناحیه را محاسبه کنیم:
با در نظر گرفتن خاصیت (6.3.8) تابع و دادن فرم فشرده تر به سمت چپ فرمول (6.3.9)، فرمولی برای احتمال یک متغیر تصادفی توزیع شده بر اساس قانون عادی به دست می آوریم. مساحت متقارن با توجه به مرکز پراکندگی:
![]() .
(6.3.10)
.
(6.3.10)
بیایید مشکل زیر را حل کنیم. اجازه دهید قطعات متوالی طول را از مرکز پراکندگی رسم کنیم (شکل 6.3.2) و احتمال سقوط یک متغیر تصادفی در هر یک از آنها را محاسبه کنیم. از آنجایی که منحنی نرمال متقارن است، کافی است چنین قطعاتی را فقط در یک جهت رسم کنیم.

با استفاده از فرمول (6.3.7) متوجه می شویم:
 (6.3.11)
(6.3.11)
همانطور که از این داده ها مشخص است، احتمال برخورد هر یک از سگمنت های زیر (پنجم، ششم و...) با دقت 001/0 برابر با صفر است.
با گرد کردن احتمالات وارد شدن به بخش ها به 0.01 (به 1٪)، سه عدد به دست می آوریم که به راحتی قابل یادآوری است:
0,34; 0,14; 0,02.
مجموع این سه مقدار 0.5 است. این به این معنی است که برای یک متغیر تصادفی با توزیع نرمال، تمام پراکندگی (با دقت کسری از درصد) در منطقه قرار می گیرد.
این اجازه می دهد تا با دانستن انحراف معیار و انتظارات ریاضی یک متغیر تصادفی، به طور تقریبی محدوده مقادیر عملا ممکن آن را نشان دهیم. این روش برای تخمین محدوده مقادیر ممکن یک متغیر تصادفی در شناخته شده است آمار ریاضی"قانون سه سیگما" نامیده می شود. قانون سه سیگما همچنین متضمن روش تقریبی برای تعیین انحراف استاندارد یک متغیر تصادفی است: حداکثر انحراف عملی ممکن را از میانگین گرفته و آن را بر سه تقسیم کنید. البته این روش خشن را تنها در صورتی می توان توصیه کرد که روش های دقیق تری برای تعیین وجود نداشته باشد.
مثال 1. یک متغیر تصادفی که بر اساس یک قانون عادی توزیع شده است نشان دهنده خطا در اندازه گیری فاصله معین است. هنگام اندازه گیری، یک خطای سیستماتیک در جهت تخمین بیش از حد 1.2 (m) مجاز است. انحراف استاندارد خطای اندازه گیری 0.8 (m) است. این احتمال را پیدا کنید که انحراف مقدار اندازه گیری شده از مقدار واقعی از 1.6 (m) در مقدار مطلق تجاوز نکند.
راه حل. خطای اندازه گیری یک متغیر تصادفی است که تابع قانون عادی با پارامترها و . باید احتمال افتادن این کمیت روی بخش از تا را پیدا کنیم. طبق فرمول (6.3.7) داریم:
با استفاده از جداول تابع (ضمیمه، جدول 1)، متوجه می شویم:
![]() ;
,
;
,
مثال 2. احتمال مشابهی را که در مثال قبل وجود داشت، بیابید، اما به شرطی که خطای سیستماتیک وجود نداشته باشد.
راه حل. با استفاده از فرمول (6.3.10)، با فرض، در می یابیم:
![]() .
.
مثال 3. هدفی که شبیه یک نوار (بزرگراه) است که عرض آن 20 متر است در جهت عمود بر بزرگراه شلیک می شود. هدف گیری در امتداد خط مرکزی بزرگراه انجام می شود. انحراف معیار در جهت تیراندازی برابر با m است. یک خطای سیستماتیک در جهت تیراندازی وجود دارد: زیر شلیک 3 متر است. احتمال برخورد به بزرگراه را با یک شلیک پیدا کنید.
صفحه 1
تست 7
قانون توزیع عادی احتمال افتادن یک متغیر تصادفی توزیع شده معمولی (NDSV) در یک بازه معین.
اطلاعات اولیه از نظریه.
توزیع احتمال یک متغیر تصادفی (RV) نرمال نامیده می شود. ایکس، اگر چگالی توزیع با معادله تعیین شود:
جایی که آ- انتظارات ریاضی SV ایکس;  - انحراف معیار.
- انحراف معیار.
برنامه  متقارن در مورد یک خط عمودی
متقارن در مورد یک خط عمودی  . هرچه بیشتر باشد، دامنه منحنی بیشتر است
. هرچه بیشتر باشد، دامنه منحنی بیشتر است  . مقادیر تابع
. مقادیر تابع  در جداول موجود است.
در جداول موجود است.
احتمال اینکه CB X مقداری متعلق به بازه را بگیرد  :
:  ، جایی که
، جایی که  - تابع لاپلاس. تابع
- تابع لاپلاس. تابع  از جداول تعیین می شود
از جداول تعیین می شود
در  منحنی =0
منحنی =0  متقارن نسبت به محور op-amp
متقارن نسبت به محور op-amp  توزیع نرمال استاندارد (یا استاندارد شده) است.
توزیع نرمال استاندارد (یا استاندارد شده) است.
از آنجایی که تابع چگالی احتمال NRSV با توجه به انتظارات ریاضی متقارن است، می توان به اصطلاح مقیاس پراکندگی را ساخت:

مشاهده می شود که با احتمال 0.9973 می توان بیان کرد که NRSV مقادیری را در بازه دریافت می کند.  . این عبارت در نظریه احتمال "قانون سه سیگما" نامیده می شود.
. این عبارت در نظریه احتمال "قانون سه سیگما" نامیده می شود.
1. مقادیر را با هم مقایسه کنید

 برای دو منحنی NRSV.
برای دو منحنی NRSV. 
1) 
 2)
2) 
2. متغیر تصادفی پیوسته X با چگالی توزیع احتمال مشخص می شود

 . سپس انتظار ریاضی از این متغیر تصادفی توزیع شده عادی برابر است با:
. سپس انتظار ریاضی از این متغیر تصادفی توزیع شده عادی برابر است با: 1) 3 2) 18 3) 4 4) 
3. NRSV X با چگالی توزیع داده می شود:  .
.
ارزش مورد انتظار  و پراکندگی این SV برابر است با:
و پراکندگی این SV برابر است با:
1)  =1 2)
=1 2)  =5 3)
=5 3)  =5
=5
 =25
=25  =1
=1  =25
=25
4. قانون سه سیگما به این معنی است که:
1) احتمال ضربه SV به فاصله  یعنی نزدیک به وحدت;
یعنی نزدیک به وحدت;
2) NRSV نمی تواند فراتر رود  ;
;
3) نمودار چگالی NRSV با توجه به انتظارات ریاضی متقارن است
5. SV X به طور معمول با انتظار ریاضی برابر با 5 و انحراف معیار برابر با 2 واحد توزیع می شود. عبارت چگالی توزیع این NRSV به شکل زیر است:
1) 
2) 
3) 
6. انتظارات ریاضی و انحراف معیار NRSV X برابر با 10 و 2 است. احتمال اینکه در نتیجه آزمون، SV X مقدار موجود در بازه را بگیرد:
1) 0,1915 2) 0,3830 3) 0,6211
7. اگر انحراف X اندازه واقعی از اندازه در نقشه در مقدار مطلق کمتر از 0.7 میلی متر باشد، قطعه مناسب در نظر گرفته می شود. انحراف X از اندازه در نقاشی NRSV با مقدار است
 = 0.4 میلی متر 100 قطعه تولید شده; از این میان موارد زیر مناسب خواهند بود:
= 0.4 میلی متر 100 قطعه تولید شده; از این میان موارد زیر مناسب خواهند بود: 1) 92 2) 64 3) 71
8. انتظارات ریاضی و انحراف معیار NRSV X برابر با 10 و 2 است. احتمال اینکه در نتیجه آزمون، SV X مقدار موجود در بازه را بگیرد این است:
1) 0,1359 2) 0,8641 3) 0,432
9. خطای X ساخت قطعه NRSV با مقدار است آ=10 و =0.1. سپس با احتمال 0.9973، فاصله اندازه قطعات متقارن با توجه به آ=10 خواهد بود:
1) 9,7; 10,3 2) 9,8; 10,2 3) 9,9; 10,1
10. همه محصولات را بدون خطاهای سیستماتیک وزن کنید. خطاهای تصادفی اندازه گیری X مشمول قانون عادی با مقدار هستند  = 10 گرم احتمال اینکه توزین با خطای بیش از 15 گرم در قدر مطلق انجام شود:
= 10 گرم احتمال اینکه توزین با خطای بیش از 15 گرم در قدر مطلق انجام شود:
1) 0,8664 2) 0,1336 3) 0,4332
11. NRSV X یک انتظار ریاضی دارد آ=10 و انحراف معیار =5. با احتمال 0.9973، مقدار X در بازه زیر قرار می گیرد:
1) (5; 15) 2) (0; 20) 3) (-5; 25)
12. NRSV X یک انتظار ریاضی دارد آ=10. مشخص است که احتمال سقوط X به بازه 0.3 است. سپس احتمال سقوط CB X در بازه برابر با:
1) 0,1 2) 0,2 3) 0,3
13. NRSV X یک انتظار ریاضی دارد آ=25. احتمال سقوط X به بازه 0.2 است. سپس احتمال سقوط X در بازه برابر خواهد بود با:
1) 0,1 2) 0,2 3) 0,3
14. دمای اتاق توسط بخاری حفظ می شود و دارای توزیع نرمال با
 و
و  . احتمال اینکه دمای این اتاق بین باشد
. احتمال اینکه دمای این اتاق بین باشد  قبل از
قبل از  است:
است: 1) 0,95 2) 0,83 3) 0,67
15. برای توزیع نرمال استاندارد شده، مقدار:
1) 1 2) 2 3) 
16. توزیع نرمال تجربی زمانی تشکیل می شود که:
1) تعداد زیادی علل تصادفی مستقل وجود دارد که وزن آماری تقریباً یکسانی دارند.
2) تعداد زیادی متغیر تصادفی وجود دارد که به شدت به یکدیگر وابسته هستند.
3) حجم نمونه کوچک است.
|
1 |
معنی  محدوده منحنی چگالی توزیع را نسبت به انتظارات ریاضی تعیین می کند. برای منحنی 2 محدوده بزرگتر است، یعنی محدوده منحنی چگالی توزیع را نسبت به انتظارات ریاضی تعیین می کند. برای منحنی 2 محدوده بزرگتر است، یعنی  |
(2) |
|
2 |
مطابق با معادله چگالی NRSV، انتظارات ریاضی آ=4. |
(3) |
|
3 |
مطابق با معادله چگالی NRSV داریم:  =1; =1;  = 5، یعنی = 5، یعنی  . .
|
(1) |
|
4 |
پاسخ (1) صحیح است. |
(1) |
|
5 |
عبارت چگالی توزیع NRSV به شکل زیر است:  . بر اساس شرط: =2; آ
=5، یعنی پاسخ (1) صحیح است. . بر اساس شرط: =2; آ
=5، یعنی پاسخ (1) صحیح است. |
(1) |
|
6 |
با شرط  =10; =10;  =2. فاصله است. سپس: =2. فاصله است. سپس:  ; ;  . .
طبق جداول تابع لاپلاس: |
(2) |
|
7 |
با شرط:  =0; =0;  ; ; =0.4. این به این معنی است که فاصله [-0.7; 0.7]. =0.4. این به این معنی است که فاصله [-0.7; 0.7].
یعنی از 100 قسمت، 92 قطعه به احتمال زیاد مناسب است. |
(1) |


|
8 |
با شرط:  =10 و =10 و  =2. فاصله است. سپس: =2. فاصله است. سپس:  ; ;  . طبق جداول تابع لاپلاس: . طبق جداول تابع لاپلاس:  ; ;  ; ;
|
(1) |
|
9 |
در یک بازه متقارن با توجه به انتظارات ریاضی آ =10 با احتمال 0.9973 همه قطعات با ابعاد برابر  ، به این معنا که ؛ . بدین ترتیب: ، به این معنا که ؛ . بدین ترتیب:   |
(1) |
|
10 |
با شرط  ،به این معنا که ،به این معنا که  = 0، و بازه زمانی [-15;15] خواهد بود. = 0، و بازه زمانی [-15;15] خواهد بود. سپس: |
واریانس یک متغیر تصادفی عادی
پراکندگیمتغیر تصادفی انتظار ریاضی مربع متغیر تصادفی متمرکز مربوطه است.
درجه پراکندگی مقادیر یک متغیر تصادفی را نسبت به انتظارات ریاضی آن مشخص می کند، به عنوان مثال. عرض محدوده مقدار
فرمول های محاسبه:
واریانس را می توان از طریق دومین لحظه اولیه محاسبه کرد:
 (6.10)
(6.10)
پراکندگی یک متغیر تصادفی، درجه پراکندگی (پراکندگی) مقادیر یک متغیر تصادفی را نسبت به انتظارات ریاضی آن مشخص می کند. واریانس SV (هم گسسته و هم پیوسته) یک کمیت غیر تصادفی (ثابت) است.
واریانس متغیر تصادفی دارای بعد مربع متغیر تصادفی است. برای وضوح، ویژگی های پراکندگی با مقداری استفاده می شود که ابعاد آن با بعد SV منطبق است.
انحراف معیار (RMS) NE ایکسمشخصه نامیده می شود
![]() . (6.11)
. (6.11)
RMSD در واحدهای فیزیکی مشابه SV اندازه گیری می شود و عرض محدوده مقادیر SV را مشخص می کند.
خواص پراکندگی
پراکندگی مقدار ثابت بابرابر با صفر
اثبات: با تعریف واریانس
هنگامی که به یک متغیر تصادفی اضافه می شود ایکسمقدار غیر تصادفی باپراکندگی آن تغییر نمی کند.
D[ایکس+ج] = D[ایکس].
اثبات: با تعریف واریانس
 (6.12)
(6.12)
3. هنگام ضرب یک متغیر تصادفی ایکسبا مقدار غیر تصادفی باواریانس آن ضرب می شود از 2.
اثبات: با تعریف واریانس
 . (6.13)
. (6.13)
برای انحراف استاندارد، این ویژگی به شکل زیر است:
![]() (6.14)
(6.14)
در واقع، برای ½С½>1 مقدار cX دارای مقادیر ممکن (در قدر مطلق) بزرگتر از مقدار X است. در نتیجه، این مقادیر در اطراف انتظارات ریاضی پراکنده می شوند. م[cX] بیشتر از مقادیر ممکن ایکسدور و بر م[ایکس]، یعنی ![]() . اگر 0<½с½<1, то
. اگر 0<½с½<1, то ![]() .
.
قانون 3.برای اکثر مقادیر یک متغیر تصادفی، مقدار مطلق انحراف آن از انتظارات ریاضی از سه برابر انحراف استاندارد تجاوز نمی کند، یا به عبارت دیگر، تقریباً تمام مقادیر SV در بازه زمانی قرار دارند:
[ متر - 3س; متر + 3 s; ].(6.15)
احتمال سقوط به یک بازه معین از یک متغیر تصادفی نرمال
همانطور که قبلاً مشخص شد، احتمال اینکه یک متغیر تصادفی پیوسته مقداری متعلق به بازه را بگیرد برابر با انتگرال معینی از چگالی توزیع است که در محدوده های مناسب گرفته شده است:  .
.
برای یک متغیر تصادفی معمولی توزیع شده به ترتیب به دست می آوریم:  .
.
بیایید آخرین عبارت را با معرفی یک متغیر جدید تبدیل کنیم  . بنابراین، توان عبارت زیر انتگرال به صورت زیر تبدیل می شود:
. بنابراین، توان عبارت زیر انتگرال به صورت زیر تبدیل می شود:  .
.
برای جایگزینی یک متغیر در یک انتگرال معین، هنوز باید دیفرانسیل و حدود انتگرال را جایگزین کرد، زیرا قبلاً متغیر را از فرمول جایگزینی بیان کرده بودیم:  ;
;
;
- حد پایین ادغام؛
- حد بالای ادغام؛
(برای یافتن حدود ادغام بر روی متغیر جدید، حدود ادغام بر متغیر قدیمی به فرمول جایگزینی متغیر جایگزین شد).
بیایید همه چیز را با آخرین فرمول جایگزین کنیم تا احتمال را پیدا کنیم: 
جایی که  – تابع لاپلاس.
– تابع لاپلاس.
نتیجه گیری: احتمال اینکه یک متغیر تصادفی با توزیع نرمال مقداری متعلق به بازه را بگیرد برابر است با:  ,
,
انتظار ریاضی کجاست و انحراف معیار یک متغیر تصادفی معین است.
23. توزیع های Chi-square، Student و Fisher
با استفاده از توزیع نرمال، سه توزیع تعریف شده است که در حال حاضر اغلب در پردازش داده های آماری استفاده می شود. این توزیعها بارها در بخشهای بعدی کتاب ظاهر میشوند.
توزیع پیرسون (کی - مربع) - توزیع یک متغیر تصادفی
متغیرهای تصادفی کجا هستند X 1، X 2،…، X nمستقل و دارای توزیع یکسانی هستند ن(0،1). در این مورد، تعداد اصطلاحات، یعنی. n، "تعداد درجات آزادی" توزیع کای اسکوئر نامیده می شود.
توزیع کای اسکوئر هنگام تخمین واریانس (با استفاده از فاصله اطمینان)، هنگام آزمایش فرضیه های توافق، همگنی، استقلال، عمدتاً برای متغیرهای کیفی (دسته بندی شده) که تعداد محدودی از مقادیر را می گیرند، و در بسیاری از وظایف دیگر داده های آماری استفاده می شود. تحلیل و بررسی.
توزیع تی t Student توزیع یک متغیر تصادفی است
متغیرهای تصادفی کجا هستند Uو ایکسمستقل، Uدارای توزیع نرمال استاندارد است ن(0.1) و ایکس– توزیع چی – مربع c nدرجه آزادی. که در آن n"تعداد درجات آزادی" توزیع دانشجو نامیده می شود.
توزیع دانشجو در سال 1908 توسط آماردان انگلیسی W. Gosset که در یک کارخانه آبجو کار می کرد، معرفی شد. برای تصمیم گیری های اقتصادی و فنی در این کارخانه از روش های احتمالی و آماری استفاده می شد، بنابراین مدیریت آن V. Gosset را از انتشار مقالات علمی به نام خود منع کرد. به این ترتیب، اسرار تجاری و "دانش" در قالب روش های احتمالی و آماری توسعه یافته توسط V. Gosset محافظت شد. با این حال او این فرصت را پیدا کرد که با نام مستعار «دانشجو» منتشر کند. تاریخچه Gosset-Student نشان می دهد که حتی صد سال پیش، مدیران در بریتانیای کبیر از کارایی اقتصادی بیشتر روش های احتمالی-آماری آگاه بودند.
در حال حاضر توزیع Student یکی از شناخته شده ترین توزیع هایی است که در تجزیه و تحلیل داده های واقعی استفاده می شود. هنگام تخمین انتظارات ریاضی، ارزش پیشبینی و سایر ویژگیها با استفاده از فواصل اطمینان، آزمون فرضیههای مربوط به مقادیر انتظارات ریاضی، ضرایب رگرسیون، فرضیههای همگنی نمونه و غیره استفاده میشود. .
 ; . سپس احتمال مورد نظر:
; . سپس احتمال مورد نظر:  ;
;  .
.
 ;
;  ;
;  .
. 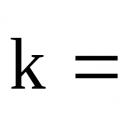 رهنمودهای ثابت سرعت واکنش برای کارهای آزمایشگاهی
رهنمودهای ثابت سرعت واکنش برای کارهای آزمایشگاهی آیا زندگی پس از مرگ وجود دارد؟
آیا زندگی پس از مرگ وجود دارد؟ دانشمندان: زمین یک "زندان فضایی" برای بشریت است دانشمندان: زمین یک زندان فضایی در جهان است
دانشمندان: زمین یک "زندان فضایی" برای بشریت است دانشمندان: زمین یک زندان فضایی در جهان است