حل مشتقات برای آدمک ها: تعریف، نحوه پیدا کردن، نمونه هایی از راه حل ها. قوانین محاسبه مشتقات مشتق تابع مختلط u v
و قضیه مشتق تابع مختلط که فرمول آن به صورت زیر است:
اجازه دهید 1) تابع $u=\varphi (x)$ در نقطه ای از $x_0$ مشتق $u_(x)"=\varphi"(x_0)$ باشد، 2) تابع $y=f(u)$ در نقطه مربوطه در نقطه $u_0=\varphi (x_0)$ مشتق $y_(u)"=f"(u)$ باشد. سپس تابع مختلط $y=f\left(\varphi (x) \right)$ در نقطه مذکور نیز مشتقی برابر حاصلضرب مشتقات توابع $f(u)$ و $\varphi خواهد داشت. x)$:
$$ \left(f(\varphi (x))\right)"=f_(u)"\left(\varphi (x_0) \right)\cdot \varphi"(x_0) $$
یا به صورت کوتاه تر: $y_(x)"=y_(u)"\cdot u_(x)"$.
در مثالهای این بخش، همه توابع به شکل $y=f(x)$ هستند (یعنی فقط توابع یک متغیر $x$ را در نظر میگیریم). بر این اساس، در همه مثالها مشتق $y"$ با توجه به متغیر $x$ گرفته شده است. برای تاکید بر اینکه مشتق با توجه به متغیر $x$ گرفته شده است، $y"_x$ اغلب به جای $y نوشته میشود. "$.
مثال های شماره 1، شماره 2 و شماره 3 روند دقیق برای یافتن مشتق را تشریح می کنند. توابع پیچیده. مثال شماره 4 برای درک کاملتر جدول مشتق در نظر گرفته شده است و منطقی است که با آن آشنا شوید.
توصیه می شود پس از مطالعه مطالب در مثال های شماره 1-3، به سراغ حل مستقل مثال های شماره 5، شماره 6 و شماره 7 بروید. مثال های 5، 6 و 7 حاوی یک راه حل کوتاه هستند تا خواننده بتواند صحت نتیجه خود را بررسی کند.
مثال شماره 1
مشتق تابع $y=e^(\cos x)$ را بیابید.
ما باید مشتق یک تابع مختلط $y"$ را پیدا کنیم. از آنجایی که $y=e^(\cos x)$، سپس $y"=\left(e^(\cos x)\right)"$. به مشتق $ \left(e^(\cos x)\right)"$ را پیدا کنید ما از فرمول شماره 6 از جدول مشتقات استفاده می کنیم. برای استفاده از فرمول شماره 6، باید این را در نظر بگیریم که در مورد ما $u=\cos x$. راه حل دیگر عبارت است از جایگزین کردن عبارت $\cos x$ به جای $u$ در فرمول شماره 6:
$$ y"=\left(e^(\cos x) \راست)"=e^(\cos x)\cdot (\cos x)" \برچسب (1.1)$$
اکنون باید مقدار عبارت $(\cos x)"$ را پیدا کنیم. دوباره به جدول مشتقات می رویم و فرمول شماره 10 را از آن انتخاب می کنیم. با جایگزینی $u=x$ به فرمول شماره 10، داریم : $(\cos x)"=-\ sin x\cdot x"$. حالا بیایید برابری (1.1) را ادامه دهیم و آن را با نتیجه یافت شده تکمیل کنیم:
$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x") \برچسب (1.2) $$
از آنجایی که $x"=1$، برابری (1.2) را ادامه می دهیم:
$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x")=e^(\cos x)\cdot (-\sin x\cdot 1)=-\sin x\cdot e^(\cos x) \برچسب (1.3) $$
بنابراین، از برابری (1.3) داریم: $y"=-\sin x\cdot e^(\cos x)$. طبیعتاً از توضیحات و برابری های میانی معمولاً صرف نظر می شود و یافته های مشتق را در یک خط یادداشت می کنیم. همانطور که در برابری (1.3) بنابراین، مشتق یک تابع مختلط پیدا شده است، تنها چیزی که باقی می ماند نوشتن پاسخ است.
پاسخ: $y"=-\sin x\cdot e^(\cos x)$.
مثال شماره 2
مشتق تابع $y=9\cdot \arctg^(12)(4\cdot \ln x)$ را بیابید.
ما باید مشتق $y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"$ را محاسبه کنیم. برای شروع، توجه می کنیم که ثابت (یعنی عدد 9) را می توان از علامت مشتق خارج کرد:
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)" \tag (2.1) $$
حال به عبارت $\left(\arctg^(12)(4\cdot \ln x) \right)"$ میپردازیم. برای سهولت در انتخاب فرمول مورد نظر از جدول مشتقات، عبارت را ارائه میکنم. سوال به این شکل: $\left( \left(\arctg(4\cdot \ln x) \right)^(12)\right)"$. اکنون مشخص است که باید از فرمول شماره 2 استفاده کرد، i.e. $\left(u^\alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. بیایید $u=\arctg(4\cdot \ln x)$ و $\alpha=12$ را در این فرمول جایگزین کنیم:

با تکمیل برابری (2.1) با نتیجه به دست آمده، داریم:
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"= 108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))" \برچسب (2.2) $$
در این شرایط، زمانی که حل کننده در مرحله اول، فرمول $(\arctg \; u)"=\frac(1)(1+u^2)\cdot u"$ را به جای فرمول انتخاب می کند، اغلب اشتباه می شود. $\left(u^\ alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. نکته این است که مشتق تابع خارجی باید اول باشد. برای درک اینکه کدام تابع خارج از عبارت $\arctg^(12)(4\cdot 5^x)$ خواهد بود، تصور کنید که مقدار عبارت $\arctg^(12)(4\cdot 5^) را محاسبه می کنید. x)$ با مقداری $x$. ابتدا مقدار $5^x$ را محاسبه می کنید، سپس نتیجه را در 4 ضرب می کنید و $4\cdot 5^x$ را بدست می آورید. حالا تانژانت را از این نتیجه می گیریم و $\arctg(4\cdot 5^x)$ را به دست می آوریم. سپس عدد حاصل را به توان دوازدهم میرسانیم و $\arctg^(12)(4\cdot 5^x)$ را میگیریم. آخرین عمل، یعنی. افزایش به توان 12 یک تابع خارجی خواهد بود. و از اینجاست که باید شروع به یافتن مشتق کنیم که در برابری انجام شد (2.2).
اکنون باید $(\arctg(4\cdot \ln x))"$ را پیدا کنیم. از فرمول شماره 19 جدول مشتقات استفاده می کنیم و $u=4\cdot \ln x$ را جایگزین آن می کنیم:
$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)" $$
بیایید با در نظر گرفتن $(4\cdot \ln x)^2=4^2\cdot (\ln x)^2=16\cdot \ln^2 x$، عبارت حاصل را کمی ساده کنیم.
$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)"=\frac( 1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" $$
برابری (2.2) اکنون تبدیل خواهد شد:
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \راست)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" \ برچسب (2.3) $$
باقی مانده است که $(4\cdot \ln x)"$ را پیدا کنیم. بیایید ثابت (یعنی 4) را از علامت مشتق خارج کنیم: $(4\cdot \ln x)"=4\cdot (\ln x)" $. برای برای پیدا کردن $(\ln x)"$ از فرمول شماره 8 استفاده می کنیم و $u=x$ را جایگزین آن می کنیم: $(\ln x)"=\frac(1)(x)\cdot x "$. از آنجایی که $x"=1$، پس $(\ln x)"=\frac(1)(x)\cdot x"=\frac(1)(x)\cdot 1=\frac(1)(x) $ با جایگزینی نتیجه به دست آمده به فرمول (2.3)، به دست می آوریم:
$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \راست)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" =\\ =108\cdot \left(\arctg(4\cdot \ln x) \راست)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot 4\ cdot \frac(1)(x)=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x)).$ $
اجازه دهید به شما یادآوری کنم که مشتق یک تابع مختلط اغلب در یک خط یافت می شود، همانطور که در آخرین برابری نوشته شده است. بنابراین، هنگام تهیه محاسبات استاندارد یا کارهای کنترلی، اصلاً نیازی به توصیف راه حل با چنین جزئیاتی نیست.
پاسخ: $y"=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x))$.
مثال شماره 3
$y"$ تابع $y=\sqrt(\sin^3(5\cdot9^x))$ را پیدا کنید.
ابتدا، اجازه دهید کمی تابع $y$ را تبدیل کنیم و رادیکال (ریشه) را به عنوان یک توان بیان کنیم: $y=\sqrt(\sin^3(5\cdot9^x))=\left(\sin(5\cdot 9) ^x) \راست)^(\frac(3)(7))$. حالا بیایید شروع به یافتن مشتق کنیم. از آنجایی که $y=\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))$، پس:
$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)" \برچسب (3.1) $$
بیایید از فرمول شماره 2 از جدول مشتقات استفاده کنیم و $u=\sin(5\cdot 9^x)$ و $\alpha=\frac(3)(7)$ را جایگزین آن کنیم:
$$ \left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"= \frac(3)(7)\cdot \left( \sin(5\cdot 9^x)\right)^(\frac(3)(7)-1) (\sin(5\cdot 9^x))"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" $$
اجازه دهید برابری (3.1) را با استفاده از نتیجه به دست آمده ادامه دهیم:
$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" \برچسب (3.2) $$
اکنون باید $(\sin(5\cdot 9^x))"$ را پیدا کنیم. برای این کار از فرمول شماره 9 از جدول مشتقات استفاده می کنیم و $u=5\cdot 9^x$ را جایگزین آن می کنیم:
$$ (\sin(5\cdot 9^x))"=\cos(5\cdot 9^x)\cdot(5\cdot 9^x)" $$
با تکمیل برابری (3.2) با نتیجه به دست آمده، داریم:
$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)" \برچسب (3.3) $$
باقی مانده است که $(5\cdot 9^x)"$ را پیدا کنیم. ابتدا ثابت (عدد $5$) را خارج از علامت مشتق بگیریم، یعنی $(5\cdot 9^x)"=5\cdot (9 ^x) "$. برای پیدا کردن مشتق $(9^x)"$، فرمول شماره 5 جدول مشتقات را اعمال کنید و $a=9$ و $u=x$ را جایگزین آن کنید: $(9^x )"=9^x\cdot \ ln9\cdot x"$. از آنجایی که $x"=1$، سپس $(9^x)"=9^x\cdot \ln9\cdot x"=9^x\cdot \ln9$. اکنون میتوانیم برابری (3.3) را ادامه دهیم:
$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)"= \frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9 ^x)\cdot 5\cdot 9^x\cdot \ln9=\\ =\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right) ^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x. $$
میتوانیم دوباره از قدرتها به رادیکالها (یعنی ریشهها) برگردیم و $\left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))$ را به شکل $\ بنویسیم. frac(1)(\left(\sin(5\cdot 9^x)\right)^(\frac(4)(7)))=\frac(1)(\sqrt(\sin^4(5\ cdot 9^x)))$. سپس مشتق به این شکل نوشته می شود:
$$ y"=\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x= \frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x) (\sqrt(\sin^4(5\cdot 9^x))).$$
پاسخ: $y"=\frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x)(\sqrt(\sin^4(5\ cdot 9^x)))$.
مثال شماره 4
نشان دهید که فرمول های شماره 3 و شماره 4 جدول مشتقات مورد خاصی از فرمول شماره 2 این جدول هستند.
فرمول شماره 2 جدول مشتقات مشتق تابع $u^\alpha$ است. با جایگزینی $\alpha=-1$ به فرمول شماره 2، دریافت می کنیم:
$$(u^(-1))"=-1\cdot u^(-1-1)\cdot u"=-u^(-2)\cdot u"\tag (4.1)$$
از آنجایی که $u^(-1)=\frac(1)(u)$ و $u^(-2)=\frac(1)(u^2)$، پس برابری (4.1) را می توان به صورت زیر بازنویسی کرد: $ \left(\frac(1)(u) \right)"=-\frac(1)(u^2)\cdot u"$. این فرمول شماره 3 جدول مشتقات است.
اجازه دهید دوباره به فرمول شماره 2 جدول مشتقات بپردازیم. بیایید $\alpha=\frac(1)(2)$ را در آن جایگزین کنیم:
$$\left(u^(\frac(1)(2))\right)"=\frac(1)(2)\cdot u^(\frac(1)(2)-1)\cdot u" =\frac(1)(2)u^(-\frac(1)(2))\cdot u"\tag (4.2) $$
از آنجایی که $u^(\frac(1)(2))=\sqrt(u)$ و $u^(-\frac(1)(2))=\frac(1)(u^(\frac( 1 )(2)))=\frac(1)(\sqrt(u))$، سپس برابری (4.2) را می توان به صورت زیر بازنویسی کرد:
$$ (\sqrt(u))"=\frac(1)(2)\cdot \frac(1)(\sqrt(u))\cdot u"=\frac(1)(2\sqrt(u) )\cdot u" $$
برابری حاصل $(\sqrt(u))"=\frac(1)(2\sqrt(u))\cdot u"$ فرمول شماره 4 جدول مشتقات است. همانطور که مشاهده می کنید فرمول های شماره 3 و شماره 4 جدول مشتق از فرمول شماره 2 با جایگزینی مقدار $\alpha$ مربوطه به دست می آیند.
حل مسائل یا مثال های فیزیکی در ریاضیات بدون آگاهی از مشتق و روش های محاسبه آن کاملاً غیرممکن است. مشتق یکی از مهمترین مفاهیم در تحلیل ریاضی است. ما تصمیم گرفتیم مقاله امروز را به این موضوع اساسی اختصاص دهیم. مشتق چیست، معنای فیزیکی و هندسی آن چیست، مشتق تابع را چگونه محاسبه کنیم؟ همه این سؤالات را می توان در یکی ترکیب کرد: چگونه مشتق را درک کنیم؟
معنای هندسی و فیزیکی مشتق
اجازه دهید یک تابع وجود داشته باشد f(x) ، در یک بازه زمانی مشخص مشخص شده است (الف، ب) . نقاط x و x0 متعلق به این بازه هستند. وقتی x تغییر می کند، خود تابع تغییر می کند. تغییر استدلال - تفاوت در مقادیر آن x-x0 . این تفاوت به صورت نوشته شده است دلتا x و افزایش آرگومان نامیده می شود. تغییر یا افزایش یک تابع، تفاوت بین مقادیر یک تابع در دو نقطه است. تعریف مشتق:
مشتق یک تابع در یک نقطه حد نسبت افزایش تابع در یک نقطه معین به افزایش آرگومان زمانی است که دومی به سمت صفر میل می کند.
در غیر این صورت می توان اینگونه نوشت:

یافتن چنین محدودیتی چه فایده ای دارد؟ و در اینجا چیست:
مشتق تابع در یک نقطه برابر است با مماس زاویه بین محور OX و مماس بر نمودار تابع در یک نقطه معین.

معنای فیزیکی مشتق: مشتق مسیر نسبت به زمان برابر است با سرعت حرکت مستقیم.
در واقع، از دوران مدرسه همه می دانند که سرعت یک مسیر خاص است x=f(t) و زمان تی . سرعت متوسط در یک بازه زمانی معین:

برای پی بردن به سرعت حرکت در یک لحظه از زمان t0 شما باید حد را محاسبه کنید:

قانون اول: یک ثابت تنظیم کنید
ثابت را می توان از علامت مشتق خارج کرد. علاوه بر این، این باید انجام شود. هنگام حل مثال هایی در ریاضیات، آن را به عنوان یک قاعده در نظر بگیرید - اگر می توانید یک عبارت را ساده کنید، حتما آن را ساده کنید .
مثال. بیایید مشتق را محاسبه کنیم:

قانون دوم: مشتق از مجموع توابع
مشتق مجموع دو تابع برابر است با مجموع مشتقات این توابع. همین امر در مورد مشتق تفاوت توابع نیز صادق است.

ما برای این قضیه اثبات نمی کنیم، بلکه یک مثال عملی را در نظر می گیریم.
مشتق تابع را پیدا کنید:


قانون سوم: مشتق حاصلضرب توابع
مشتق حاصل ضرب دو تابع متمایز با فرمول محاسبه می شود:

مثال: مشتق یک تابع را پیدا کنید:

راه حل: 
در اینجا مهم است که در مورد محاسبه مشتقات توابع پیچیده صحبت کنیم. مشتق تابع مختلط با حاصلضرب مشتق این تابع نسبت به آرگومان میانی و مشتق آرگومان میانی نسبت به متغیر مستقل برابر است.
در مثال بالا به این عبارت برخورد می کنیم:

در این حالت، آرگومان میانی 8 برابر به توان پنجم است. برای محاسبه مشتق چنین عبارتی، ابتدا مشتق تابع خارجی را با توجه به آرگومان میانی محاسبه می کنیم و سپس آن را در مشتق خود آرگومان میانی نسبت به متغیر مستقل ضرب می کنیم.
قانون چهارم: مشتق ضریب دو تابع
فرمول تعیین مشتق ضریب دو تابع:



ما سعی کردیم در مورد مشتقات برای آدمک ها از ابتدا صحبت کنیم. این موضوع آنقدرها هم که به نظر می رسد ساده نیست، پس اخطار داشته باشید: در مثال ها اغلب مشکلاتی وجود دارد، بنابراین هنگام محاسبه مشتقات مراقب باشید.
در صورت داشتن هرگونه سوال در این زمینه و موضوعات دیگر، می توانید با خدمات دانشجویی تماس بگیرید. در مدت زمان کوتاهی، ما به شما کمک می کنیم تا سخت ترین آزمون را حل کنید و وظایف را درک کنید، حتی اگر قبلاً محاسبات مشتق را انجام نداده باشید.
اگر از تعریف پیروی کنید، مشتق یک تابع در یک نقطه حد نسبت افزایش تابع Δ است. yبه آرگومان افزایش Δ ایکس:
به نظر می رسد همه چیز روشن است. اما سعی کنید از این فرمول برای محاسبه مشتق تابع استفاده کنید f(ایکس) = ایکس 2 + (2ایکس+ 3) · ه ایکسگناه ایکس. اگر همه کارها را طبق تعریف انجام دهید، پس از چند صفحه محاسبات به سادگی می خوابید. بنابراین، راه های ساده تر و موثرتری وجود دارد.
برای شروع، ما توجه می کنیم که از کل توابع مختلف می توانیم به اصطلاح توابع ابتدایی را تشخیص دهیم. اینها عبارات نسبتاً ساده ای هستند که مشتقات آنها مدتهاست محاسبه و جدول بندی شده است. یادآوری چنین توابعی بسیار آسان است - همراه با مشتقات آنها.
مشتقات توابع ابتدایی
توابع ابتدایی همه آنهایی هستند که در زیر لیست شده اند. مشتقات این توابع را باید از روی قلب دانست. علاوه بر این ، به خاطر سپردن آنها اصلاً دشوار نیست - به همین دلیل آنها ابتدایی هستند.
بنابراین، مشتقات توابع ابتدایی:
| نام | تابع | مشتق |
| ثابت | f(ایکس) = سی, سی ∈ آر | 0 (بله، صفر!) |
| قدرت با توان منطقی | f(ایکس) = ایکس n | n · ایکس n − 1 |
| سینوسی | f(ایکس) = گناه ایکس | cos ایکس |
| کسینوس | f(ایکس) = cos ایکس | -گناه ایکس(منهای سینوس) |
| مماس | f(ایکس) = tg ایکس | 1/cos 2 ایکس |
| کوتانژانت | f(ایکس) = ctg ایکس | − 1/گناه 2 ایکس |
| لگاریتم طبیعی | f(ایکس) = ورود ایکس | 1/ایکس |
| لگاریتم دلخواه | f(ایکس) = ورود آ ایکس | 1/(ایکسلوگاریتم آ) |
| تابع نمایی | f(ایکس) = ه ایکس | ه ایکس(هیچ چیز تغییر نکرد) |
اگر یک تابع ابتدایی در یک ثابت دلخواه ضرب شود، مشتق تابع جدید نیز به راحتی محاسبه می شود:
(سی · f)’ = سی · f ’.
به طور کلی، ثابت ها را می توان از علامت مشتق خارج کرد. مثلا:
(2ایکس 3)' = 2 · ( ایکس 3) = 2 3 ایکس 2 = 6ایکس 2 .
بدیهی است که توابع ابتدایی را می توان به یکدیگر اضافه کرد، ضرب کرد، تقسیم کرد - و موارد دیگر. به این ترتیب توابع جدید ظاهر می شوند، نه به ویژه ابتدایی، بلکه طبق قوانین خاصی متمایز می شوند. این قوانین در زیر مورد بحث قرار می گیرند.
مشتق جمع و تفاوت
اجازه دهید توابع داده شوند f(ایکس) و g(ایکس) که مشتقات آن برای ما معلوم است. به عنوان مثال، می توانید توابع ابتدایی مورد بحث در بالا را انتخاب کنید. سپس می توانید مشتق حاصل از مجموع و تفاضل این توابع را پیدا کنید:
- (f + g)’ = f ’ + g ’
- (f − g)’ = f ’ − g ’
پس مشتق مجموع (تفاوت) دو تابع برابر با مجموع (تفاوت) مشتقات است. ممکن است شرایط بیشتری وجود داشته باشد. مثلا، ( f + g + ساعت)’ = f ’ + g ’ + ساعت ’.
به بیان دقیق، هیچ مفهومی از "تفریق" در جبر وجود ندارد. مفهوم "عنصر منفی" وجود دارد. بنابراین تفاوت f − gرا می توان به صورت جمع بازنویسی کرد f+ (-1) g، و سپس فقط یک فرمول باقی می ماند - مشتق جمع.
f(ایکس) = ایکس 2 + گناه x; g(ایکس) = ایکس 4 + 2ایکس 2 − 3.
تابع f(ایکس) مجموع دو تابع ابتدایی است، بنابراین:
f ’(ایکس) = (ایکس 2 + گناه ایکس)’ = (ایکس 2)’ + (گناه ایکس)’ = 2ایکس+ cos x;
ما به طور مشابه برای تابع استدلال می کنیم g(ایکس). فقط سه اصطلاح وجود دارد (از نظر جبر):
g ’(ایکس) = (ایکس 4 + 2ایکس 2 − 3)’ = (ایکس 4 + 2ایکس 2 + (−3))’ = (ایکس 4)’ + (2ایکس 2)’ + (−3)’ = 4ایکس 3 + 4ایکس + 0 = 4ایکس · ( ایکس 2 + 1).
پاسخ:
f ’(ایکس) = 2ایکس+ cos x;
g ’(ایکس) = 4ایکس · ( ایکس
2 + 1).
مشتق محصول
ریاضیات یک علم منطقی است، بنابراین بسیاری از مردم معتقدند که اگر مشتق یک مجموع برابر با مجموع مشتقات باشد، پس مشتق حاصلضرب ضربه">برابر حاصلضرب مشتقات است. اما شما را خراب کنید! مشتق یک محصول با استفاده از یک فرمول کاملاً متفاوت محاسبه می شود. یعنی:
(f · g) ’ = f ’ · g + f · g ’
فرمول ساده است، اما اغلب فراموش می شود. و نه تنها دانش آموزان، بلکه دانش آموزان نیز. نتیجه مشکلات حل نادرست است.
وظیفه. مشتقات توابع را پیدا کنید: f(ایکس) = ایکس 3 cos x; g(ایکس) = (ایکس 2 + 7ایکس− 7) · ه ایکس .
تابع f(ایکس) حاصل دو تابع ابتدایی است، بنابراین همه چیز ساده است:
f ’(ایکس) = (ایکس 3 cos ایکس)’ = (ایکس 3)’ cos ایکس + ایکس 3 (Cos ایکس)’ = 3ایکس 2 cos ایکس + ایکس 3 (- گناه ایکس) = ایکس 2 (3cos ایکس − ایکسگناه ایکس)
تابع g(ایکس) ضریب اول کمی پیچیده تر است، اما طرح کلی تغییر نمی کند. بدیهی است که اولین عامل تابع g(ایکس) چند جمله ای است و مشتق آن مشتق جمع است. ما داریم:
g ’(ایکس) = ((ایکس 2 + 7ایکس− 7) · ه ایکس)’ = (ایکس 2 + 7ایکس− 7)» · ه ایکس + (ایکس 2 + 7ایکس− 7) · ( ه ایکس)’ = (2ایکس+ 7) · ه ایکس + (ایکس 2 + 7ایکس− 7) · ه ایکس = ه ایکس· (2 ایکس + 7 + ایکس 2 + 7ایکس −7) = (ایکس 2 + 9ایکس) · ه ایکس = ایکس(ایکس+ 9) · ه ایکس .
پاسخ:
f ’(ایکس) = ایکس 2 (3cos ایکس − ایکسگناه ایکس);
g ’(ایکس) = ایکس(ایکس+ 9) · ه
ایکس
.
لطفا توجه داشته باشید که در مرحله آخر مشتق فاکتور می شود. به طور رسمی، این کار نیازی به انجام ندارد، اما بیشتر مشتقات به تنهایی محاسبه نمی شوند، بلکه برای بررسی تابع محاسبه می شوند. این بدان معنی است که در ادامه مشتق برابر با صفر می شود، علائم آن مشخص می شود و غیره. برای چنین موردی بهتر است یک عبارت فاکتوریزه شود.
اگر دو عملکرد وجود دارد f(ایکس) و g(ایکس) و g(ایکس) ≠ 0 در مجموعه ای که به آن علاقه داریم، می توانیم یک تابع جدید تعریف کنیم ساعت(ایکس) = f(ایکس)/g(ایکس). برای چنین تابعی می توانید مشتق را نیز پیدا کنید:
ضعیف نیست، نه؟ منهای از کجا آمد؟ چرا g 2؟ و مثل این! این یکی از پیچیده ترین فرمول ها است - بدون بطری نمی توانید آن را بفهمید. بنابراین بهتر است با مثال های مشخص آن را مطالعه کنید.
وظیفه. مشتقات توابع را پیدا کنید:
صورت و مخرج هر کسر حاوی توابع ابتدایی است، بنابراین تنها چیزی که ما نیاز داریم فرمول مشتق ضریب است:
طبق سنت، بیایید شمارنده را فاکتورسازی کنیم - این پاسخ را بسیار ساده می کند:
یک تابع پیچیده لزوماً یک فرمول به طول نیم کیلومتر نیست. برای مثال کافی است تابع را بگیرید f(ایکس) = گناه ایکسو متغیر را جایگزین کنید ایکس، بگو ، در ایکس 2 + ln ایکس. نتیجه خواهد داد f(ایکس) = گناه ( ایکس 2 + ln ایکس) - این یک تابع پیچیده است. یک مشتق نیز دارد، اما یافتن آن با استفاده از قوانینی که در بالا توضیح داده شد ممکن نخواهد بود.
باید چکار کنم؟ در چنین مواردی، جایگزینی یک متغیر و فرمول برای مشتق یک تابع مختلط کمک می کند:
f ’(ایکس) = f ’(تی) · تی'، اگر ایکسجایگزین می شود تی(ایکس).
به عنوان یک قاعده، وضعیت درک این فرمول حتی غم انگیزتر از مشتق ضریب است. بنابراین بهتر است آن را نیز با مثال های مشخص، با توصیف همراه با جزئیاتهر قدم.
وظیفه. مشتقات توابع را پیدا کنید: f(ایکس) = ه 2ایکس + 3 ; g(ایکس) = گناه ( ایکس 2 + ln ایکس)
توجه داشته باشید که اگر در تابع f(ایکس) به جای عبارت 2 ایکس+ 3 آسان خواهد بود ایکس، سپس یک تابع ابتدایی دریافت می کنیم f(ایکس) = ه ایکس. بنابراین، ما یک جایگزین می کنیم: اجازه دهید 2 ایکس + 3 = تی, f(ایکس) = f(تی) = ه تی. ما مشتق یک تابع مختلط را با استفاده از فرمول جستجو می کنیم:
f ’(ایکس) = f ’(تی) · تی ’ = (ه تی)’ · تی ’ = ه تی · تی ’
و اکنون - توجه! ما جایگزینی معکوس را انجام می دهیم: تی = 2ایکس+ 3. دریافت می کنیم:
f ’(ایکس) = ه تی · تی ’ = ه 2ایکس+ 3 (2 ایکس + 3)’ = ه 2ایکس+ 3 2 = 2 ه 2ایکس + 3
حالا بیایید به تابع نگاه کنیم g(ایکس). بدیهی است که باید تعویض شود ایکس 2 + ln ایکس = تی. ما داریم:
g ’(ایکس) = g ’(تی) · تی= (گناه تی)’ · تی= cos تی · تی ’
تعویض معکوس: تی = ایکس 2 + ln ایکس. سپس:
g ’(ایکس) = cos ( ایکس 2 + ln ایکس) · ( ایکس 2 + ln ایکس)’ = cos ( ایکس 2 + ln ایکس) · (2 ایکس + 1/ایکس).
همین! همانطور که از عبارت آخر مشاهده می شود، کل مسئله به محاسبه مجموع مشتق تقلیل یافته است.
پاسخ:
f ’(ایکس) = 2 · ه
2ایکس + 3 ;
g ’(ایکس) = (2ایکس + 1/ایکس) cos ( ایکس 2 + ln ایکس).
اغلب در درسهایم، بهجای اصطلاح «مشتق»، از کلمه «اول» استفاده میکنم. به عنوان مثال، ضربه از مجموع برابر است با مجموع ضربه. این واضح تر است؟ خوب، این خوب است.
بنابراین، محاسبه مشتق به خلاص شدن از شر همین سکته ها طبق قوانینی که در بالا توضیح داده شد، ختم می شود. به عنوان مثال آخر، اجازه دهید به توان مشتق با توان گویا برگردیم:
(ایکس n)’ = n · ایکس n − 1
تعداد کمی از مردم آن را در نقش می دانند nممکن است یک عدد کسری باشد. به عنوان مثال، ریشه است ایکس 0.5. اگر چیزی فانتزی زیر ریشه باشد چه؟ باز هم، نتیجه یک عملکرد پیچیده خواهد بود - آنها دوست دارند چنین ساختارهایی را به آنها بدهند تست هاو امتحانات
وظیفه. مشتق تابع را پیدا کنید:
ابتدا، بیایید ریشه را به عنوان یک توان با توان گویا بازنویسی کنیم:
f(ایکس) = (ایکس 2 + 8ایکس − 7) 0,5 .
حالا ما جایگزین می کنیم: اجازه دهید ایکس 2 + 8ایکس − 7 = تی. ما مشتق را با استفاده از فرمول پیدا می کنیم:
f ’(ایکس) = f ’(تی) · تی ’ = (تی 0.5) · تی' = 0.5 · تی−0.5 · تی ’.
بیایید جایگزینی معکوس را انجام دهیم: تی = ایکس 2 + 8ایکس− 7. داریم:
f ’(ایکس) = 0.5 · ( ایکس 2 + 8ایکس− 7) −0.5 · ( ایکس 2 + 8ایکس− 7) = 0.5 · (2 ایکس+ 8) ( ایکس 2 + 8ایکس − 7) −0,5 .
در نهایت، به ریشه ها بازگردیم:
خیلی راحت به خاطر سپردن
خوب، بیایید دور نرویم، بیایید فوراً به آن نگاه کنیم تابع معکوس. کدام تابع معکوس تابع نمایی است؟ لگاریتم:
در مورد ما، پایه عدد است:
چنین لگاریتمی (یعنی لگاریتمی با پایه) "طبیعی" نامیده می شود و ما از نماد خاصی برای آن استفاده می کنیم: به جای آن می نویسیم.
با چه چیزی برابر است؟ البته، .
مشتق لگاریتم طبیعی نیز بسیار ساده است:
مثال ها:
- مشتق تابع را بیابید.
- مشتق تابع چیست؟
پاسخ ها: لگاریتم نمایی و طبیعی از دیدگاه مشتق، توابع ساده منحصر به فردی هستند. توابع نمایی و لگاریتمی با هر پایه دیگری مشتق متفاوتی خواهند داشت که بعد از مرور قوانین تمایز آن را تحلیل خواهیم کرد.
قوانین تمایز
قوانین چی؟ بازم یه ترم جدید دیگه؟!...
تفکیکفرآیند یافتن مشتق است.
همین. این فرآیند را در یک کلمه چه چیز دیگری میتوان نامید؟ نه مشتق... ریاضیدانان دیفرانسیل را همان افزایش یک تابع در می نامند. این اصطلاح از دیفرانسیل لاتین - تفاوت می آید. اینجا.
هنگام استخراج همه این قوانین، از دو تابع به عنوان مثال و. ما همچنین به فرمول هایی برای افزایش آنها نیاز خواهیم داشت:
در کل 5 قانون وجود دارد.
ثابت از علامت مشتق خارج می شود.
اگر - یک عدد ثابت (ثابت)، پس.
بدیهی است که این قانون برای تفاوت نیز کار می کند: .
بیایید ثابت کنیم. بگذارید باشد یا ساده تر.
مثال ها.
مشتقات توابع را پیدا کنید:
- در یک نقطه؛
- در یک نقطه؛
- در یک نقطه؛
- در نقطه
راه حل ها:
- (مشتق در همه نقاط یکسان است، زیرا این تابع خطی، یاد آوردن؟)؛
مشتق محصول
همه چیز در اینجا مشابه است: بیایید یک تابع جدید معرفی کنیم و افزایش آن را پیدا کنیم:
مشتق:
مثال ها:
- مشتقات توابع را پیدا کنید و
- مشتق تابع را در یک نقطه پیدا کنید.
راه حل ها:
مشتق تابع نمایی
اکنون دانش شما کافی است تا یاد بگیرید که چگونه مشتق هر تابع نمایی را بیابید، و نه فقط نماها (آیا هنوز فراموش کرده اید که چیست؟).
بنابراین، تعدادی از آن ها کجاست.
ما قبلاً مشتق تابع را می دانیم، بنابراین بیایید سعی کنیم تابع خود را به یک پایه جدید کاهش دهیم:
برای این کار از یک قانون ساده استفاده می کنیم: . سپس:
خوب، کار کرد. حالا سعی کنید مشتق را پیدا کنید و فراموش نکنید که این تابع پیچیده است.
اتفاق افتاد؟
در اینجا، خود را بررسی کنید:
این فرمول بسیار شبیه به مشتق یک توان است: همانطور که بود، ثابت می ماند، فقط یک عامل ظاهر شد که فقط یک عدد است، اما یک متغیر نیست.
مثال ها:
مشتقات توابع را پیدا کنید:
پاسخ ها:
این فقط یک عدد است که بدون ماشین حساب نمی توان آن را محاسبه کرد، یعنی دیگر نمی توان آن را یادداشت کرد. به شکل ساده. لذا در جواب به این شکل می گذاریم.
توجه داشته باشید که در اینجا ضریب دو تابع است، بنابراین قانون تمایز مربوطه را اعمال می کنیم:
در این مثال حاصل ضرب دو تابع:
مشتق تابع لگاریتمی
در اینجا مشابه است: شما قبلاً مشتق لگاریتم طبیعی را می دانید:
بنابراین، برای پیدا کردن یک لگاریتم دلخواه با پایه متفاوت، به عنوان مثال:
باید این لگاریتم را به پایه کاهش دهیم. چگونه پایه لگاریتم را تغییر می دهید؟ امیدوارم این فرمول را به خاطر داشته باشید:
فقط اکنون به جای آن می نویسیم:
مخرج به سادگی یک ثابت است (عددی ثابت، بدون متغیر). مشتق بسیار ساده به دست می آید:
مشتقات توابع نمایی و لگاریتمی تقریباً هرگز در آزمون یکپارچه دولتی یافت نمی شوند، اما دانستن آنها اضافی نخواهد بود.
مشتق تابع مختلط
"تابع پیچیده" چیست؟ نه، این یک لگاریتم نیست و نه یک تانژانت. درک این توابع ممکن است دشوار باشد (البته اگر لگاریتم برای شما دشوار است، مبحث "لگاریتم" را بخوانید و خوب خواهید شد)، اما از نظر ریاضی، کلمه "پیچیده" به معنای "دشوار" نیست.
یک تسمه نقاله کوچک را تصور کنید: دو نفر نشسته اند و با برخی از اشیا کارهایی را انجام می دهند. به عنوان مثال، اولی یک تخته شکلات را در یک بسته بندی می پیچد و دومی آن را با یک روبان می بندد. نتیجه یک شی ترکیبی است: یک شکلات که با روبان بسته شده و بسته شده است. برای خوردن یک شکلات تخته ای، باید مراحل معکوس را به ترتیب معکوس انجام دهید.
بیایید یک خط لوله ریاضی مشابه ایجاد کنیم: ابتدا کسینوس یک عدد را پیدا می کنیم و سپس عدد حاصل را مربع می کنیم. بنابراین، یک عدد (شکلاتی) به ما داده می شود، من کسینوس آن را پیدا می کنم (لفاف بندی)، و سپس شما آنچه را که به دست آوردم مربع می کنید (آن را با یک روبان ببندید). چی شد؟ تابع. این مثالی از یک تابع پیچیده است: زمانی که برای یافتن مقدار آن، اولین عمل را مستقیماً با متغیر انجام می دهیم، و سپس یک عمل دوم را با آنچه که از اولی حاصل می شود، انجام می دهیم.
به عبارت دیگر، تابع پیچیده تابعی است که آرگومان آن تابع دیگری است: .
برای مثال ما، .
ما به راحتی میتوانیم همان مراحل را به ترتیب معکوس انجام دهیم: ابتدا آن را مربع میکنید و من به دنبال کسینوس عدد حاصل میگردم: . به راحتی می توان حدس زد که نتیجه تقریباً همیشه متفاوت خواهد بود. یک ویژگی مهم توابع پیچیده: وقتی ترتیب اعمال تغییر می کند، تابع تغییر می کند.
مثال دوم: (همان چیز). .
عملی که آخرین بار انجام می دهیم نامیده می شود عملکرد "خارجی".، و عمل انجام شد - بر این اساس عملکرد "داخلی".(این اسامی غیر رسمی هستند، من از آنها فقط برای توضیح مطالب به زبان ساده استفاده می کنم).
سعی کنید خودتان تعیین کنید کدام تابع خارجی و کدام داخلی است:
پاسخ ها:جداسازی توابع داخلی و خارجی بسیار شبیه به تغییر متغیرها است: به عنوان مثال، در یک تابع
- ابتدا چه اقدامی را انجام خواهیم داد؟ ابتدا بیایید سینوس را محاسبه کنیم و فقط آن را مکعب کنیم. این بدان معنی است که یک عملکرد داخلی است، اما یک عملکرد خارجی.
و کارکرد اصلی ترکیب آنهاست: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: . - درونی؛ داخلی: ؛ خارجی: .
معاینه: .
متغیرها را تغییر می دهیم و یک تابع می گیریم.
خوب، حالا شکلاتمان را استخراج میکنیم و به دنبال مشتق آن میگردیم. روال همیشه برعکس است: ابتدا مشتق تابع بیرونی را جستجو می کنیم، سپس نتیجه را در مشتق تابع درونی ضرب می کنیم. در رابطه با نمونه اصلی، به این صورت است:
مثالی دیگر:
بنابراین، اجازه دهید در نهایت قانون رسمی را فرموله کنیم:
الگوریتم یافتن مشتق تابع مختلط:
ساده به نظر می رسد، درست است؟
بیایید با مثال ها بررسی کنیم:
راه حل ها:
1) داخلی:
خارجی: ;
2) داخلی:
(فقط سعی نکنید تا الان آن را قطع کنید! چیزی از زیر کسینوس بیرون نمی آید، یادتان هست؟)
3) داخلی:
خارجی: ;
بلافاصله مشخص می شود که این یک عملکرد پیچیده سه سطحی است: از این گذشته ، این به خودی خود یک عملکرد پیچیده است و ما ریشه را نیز از آن استخراج می کنیم ، یعنی عمل سوم را انجام می دهیم (شکلات را در یک بسته بندی قرار می دهیم. و با یک روبان در کیف). اما دلیلی برای ترس وجود ندارد: ما همچنان این عملکرد را به همان ترتیب معمول "باز کردن" خواهیم کرد: از پایان.
یعنی ابتدا ریشه و بعد کسینوس و فقط بعد عبارت داخل پرانتز را متمایز می کنیم. و سپس همه را ضرب می کنیم.
در چنین مواردی، شماره گذاری اقدامات راحت است. یعنی آنچه را که می دانیم تصور کنیم. به چه ترتیبی اقداماتی را برای محاسبه مقدار این عبارت انجام خواهیم داد؟ بیایید به یک مثال نگاه کنیم:
هرچه این عمل دیرتر انجام شود، عملکرد مربوطه "خارجی" تر خواهد بود. توالی اقدامات مانند قبل است:
در اینجا لانه سازی به طور کلی 4 سطح است. بیایید مسیر عمل را مشخص کنیم.
1. بیان رادیکال. .
2. ریشه. .
3. سینوس. .
4. مربع. .
5. کنار هم گذاشتن همه:
مشتق. به طور خلاصه در مورد چیزهای اصلی
مشتق یک تابع- نسبت افزایش تابع به افزایش آرگومان برای افزایش بی نهایت کوچک آرگومان:
مشتقات پایه:
قوانین تمایز:
ثابت از علامت مشتق خارج می شود:
مشتق جمع:
مشتقات محصول:
مشتق ضریب:
مشتق تابع مختلط:
الگوریتم یافتن مشتق تابع مختلط:
- ما تابع "داخلی" را تعریف کرده و مشتق آن را پیدا می کنیم.
- ما تابع "خارجی" را تعریف می کنیم و مشتق آن را پیدا می کنیم.
- نتایج نقطه اول و دوم را ضرب می کنیم.
از زمانی که به اینجا آمدید، احتمالاً قبلاً این فرمول را در کتاب درسی دیده اید
و چهره ای مانند این بسازید:
دوست، نگران نباش! در واقع، همه چیز به سادگی ظالمانه است. قطعا همه چیز را خواهید فهمید. فقط یک درخواست - مقاله را بخوانید به آرامی، سعی کنید هر مرحله را درک کنید. من تا حد امکان ساده و واضح نوشتم، اما هنوز باید ایده را درک کنید. و حتماً وظایف را از مقاله حل کنید.
تابع پیچیده چیست؟
تصور کنید که به آپارتمان دیگری نقل مکان می کنید و بنابراین وسایل را در جعبه های بزرگ بسته بندی می کنید. فرض کنید باید چند اقلام کوچک را جمع آوری کنید، به عنوان مثال، نوشت افزار مدرسه. اگر فقط آنها را در یک جعبه بزرگ بیندازید، در میان چیزهای دیگر گم می شوند. برای جلوگیری از این امر، ابتدا آنها را مثلاً در یک کیسه قرار می دهید، سپس آن را در یک جعبه بزرگ قرار می دهید و بعد آن را مهر و موم می کنید. این فرآیند "پیچیده" در نمودار زیر ارائه شده است:

به نظر می رسد، ریاضیات چه ربطی به آن دارد؟ بله، علیرغم این واقعیت که یک تابع پیچیده دقیقاً به همین روش تشکیل می شود! فقط ما نه دفترچه و خودکار، بلکه \(x\) "بسته بندی" می کنیم، در حالی که "بسته ها" و "جعبه ها" متفاوت هستند.
برای مثال، بیایید x را بگیریم و آن را در یک تابع "بسته" کنیم:

در نتیجه، مطمئناً \(\cosx\) را دریافت می کنیم. این "کیف چیزهای" ماست. حالا بیایید آن را در یک "جعبه" قرار دهیم - آن را به عنوان مثال در یک تابع مکعبی بسته بندی کنیم.

در نهایت چه اتفاقی خواهد افتاد؟ بله، درست است، یک "کیسه چیز در یک جعبه" وجود خواهد داشت، یعنی "کسینوس مکعب X".

طراحی به دست آمده یک عملکرد پیچیده است. از این جهت با ساده تفاوت دارد چندین "تأثیر" (بسته) روی یک X در یک ردیف اعمال می شودو به نظر می رسد "عملکرد از عملکرد" - "بسته بندی در بسته بندی".
در دوره مدرسه انواع بسیار کمی از این "بسته ها" وجود دارد، فقط چهار نوع:

بیایید اکنون X را ابتدا در یک تابع نمایی با پایه 7 و سپس در یک تابع مثلثاتی قرار دهیم. ما گرفتیم:
\(x → 7^x → tg(7^x)\)
حالا بیایید X را دو بار داخل "بسته بندی" کنیم توابع مثلثاتی، ابتدا در و سپس در:
\(x → sinx → cotg (sinx)\)
ساده است، درست است؟
حالا توابع را خودتان بنویسید، جایی که x:
- ابتدا در یک کسینوس و سپس در یک تابع نمایی با پایه \(3\) "بسته بندی" می شود.
- ابتدا به توان پنجم و سپس به مماس.
- ابتدا به لگاریتم به پایه \(4\)
، سپس به توان \(-2\).
پاسخ این کار را در انتهای مقاله بیابید.
آیا می توانیم X را نه دو، بلکه سه بار "بسته" کنیم؟ مشکلی نیست! و چهار و پنج و بیست و پنج بار. برای مثال، در اینجا تابعی است که در آن x \(4\) بار "بسته" شده است:
\(y=5^(\log_2(\sin(x^4)))\)
اما چنین فرمول هایی در تمرین مدرسه یافت نمی شوند (دانش آموزان خوش شانس تر هستند - ممکن است فرمول آنها پیچیده تر باشد).
"باز کردن بسته بندی" یک عملکرد پیچیده
دوباره به عملکرد قبلی نگاه کنید. آیا می توانید دنباله "بسته بندی" را بفهمید؟ ابتدا X در چه چیزی قرار گرفت، سپس چه چیزی، و به همین ترتیب تا آخر کار. یعنی کدام تابع درون کدام تودرتو است؟ یک تکه کاغذ بردارید و آنچه را که فکر می کنید بنویسید. همانطور که در بالا نوشتیم می توانید این کار را با یک زنجیره با فلش انجام دهید یا به روش دیگری.
حال پاسخ صحیح این است: ابتدا x به توان \(4\)ام بسته شد، سپس نتیجه در یک سینوس بسته بندی شد و به نوبه خود در لگاریتم به پایه \(2\) قرار گرفت. ، و در پایان کل این سازه در یک پاور پنج قرار گرفت.
یعنی باید دنباله را به ترتیب معکوس باز کنید. و در اینجا یک نکته در مورد چگونگی انجام این کار ساده تر است: فوراً به X نگاه کنید - باید از روی آن برقصید. بیایید به چند نمونه نگاه کنیم.
به عنوان مثال، در اینجا تابع زیر است: \(y=tg(\log_2x)\). ما به X نگاه می کنیم - ابتدا چه اتفاقی برای آن می افتد؟ از او گرفته شده است. و سپس؟ مماس حاصل گرفته می شود. دنباله یکسان خواهد بود:
\(x → \log_2x → tg(\log_2x)\)
مثال دیگر: \(y=\cos((x^3))\). بیایید تجزیه و تحلیل کنیم - ابتدا X را مکعب کردیم و سپس کسینوس نتیجه را گرفتیم. این بدان معنی است که دنباله به این صورت خواهد بود: \(x → x^3 → \cos((x^3))\). توجه کنید، به نظر می رسد عملکرد شبیه به اولین (جایی که تصاویر دارد) است. اما این یک تابع کاملاً متفاوت است: اینجا در مکعب x است (یعنی \(\cos((x·x·x)))\) و در مکعب کسینوس \(x\) است ( یعنی \(\cos x·\cosx·\cosx\)). این تفاوت از توالی های مختلف "بسته بندی" ناشی می شود.
آخرین مثال (با اطلاعات مهم در آن): \(y=\sin((2x+5))\). معلوم است اول اینجا چه کردند عملیات حسابیبا x، سپس سینوس حاصل را گرفت: \(x → 2x+5 → \sin((2x+5))\). و این نکته مهم: علیرغم اینکه عملیات حسابی به خودی خود توابع نیستند، در اینجا به عنوان یک روش "بسته بندی" نیز عمل می کنند. بیایید کمی عمیق تر به این ظرافت بپردازیم.
همانطور که در بالا گفتم، در توابع ساده x یک بار و در توابع پیچیده - دو یا بیشتر بسته می شود. علاوه بر این، هر ترکیبی از توابع ساده (یعنی مجموع، تفاوت، ضرب یا تقسیم آنها) نیز عملکرد ساده. برای مثال، \(x^7\) یک تابع ساده است و همچنین \(ctg x\). این بدان معنی است که همه ترکیبات آنها توابع ساده هستند:
\(x^7+ ctg x\) - ساده،
\(x^7· تخت x\) - ساده،
\(\frac(x^7)(ctg x)\) - ساده و غیره.
با این حال، اگر یک تابع دیگر برای چنین ترکیبی اعمال شود، به یک تابع پیچیده تبدیل می شود، زیرا دو "بسته" وجود خواهد داشت. نمودار را ببینید:

باشه حالا برو جلو دنباله توابع "پیچیدن" را بنویسید:
\(y=cos((sinx))\)
\(y=5^(x^7)\)
\(y=arctg(11^x)\)
\(y=log_2(1+x)\)
پاسخ ها دوباره در انتهای مقاله آمده است.
عملکردهای داخلی و خارجی
چرا باید تودرتوی تابع را درک کنیم؟ این چه چیزی به ما می دهد؟ واقعیت این است که بدون چنین تحلیلی نمیتوانیم مشتقاتی از توابع مورد بحث در بالا را به طور قابل اعتماد پیدا کنیم.
و برای حرکت به دو مفهوم دیگر نیاز داریم: عملکردهای داخلی و خارجی. این یک چیز بسیار ساده است، علاوه بر این، در واقع، ما قبلا آنها را در بالا تجزیه و تحلیل کرده ایم: اگر قیاس خود را در همان ابتدا به یاد بیاوریم، تابع داخلی یک "بسته" است و تابع خارجی یک "جعبه" است. آن ها چیزی که X ابتدا در آن "پیچیده شده" یک تابع داخلی است، و آنچه که تابع داخلی "پیچیده شده" در آن قبلاً خارجی است. خوب، واضح است که چرا - او بیرون است، این به معنای خارجی است.
در این مثال: \(y=tg(log_2x)\)، تابع \(\log_2x\) داخلی است، و  - خارجی
- خارجی
و در این: \(y=\cos((x^3+2x+1))\)، \(x^3+2x+1\) داخلی است، و  - خارجی
- خارجی
آخرین تمرین تجزیه و تحلیل توابع پیچیده را کامل کنید، و در نهایت به آنچه که همه ما برای آن شروع کرده بودیم، برویم - مشتقاتی از توابع پیچیده را خواهیم یافت:
جاهای خالی جدول را پر کنید:
مشتق تابع مختلط
آفرین به ما، بالاخره به "رئیس" این مبحث رسیدیم - در واقع، مشتق یک تابع پیچیده، و به طور خاص، به آن فرمول بسیار وحشتناک از ابتدای مقاله.☺
\((f(g(x)))"=f"(g(x))\cdot g"(x)\)
این فرمول به این صورت است:
مشتق تابع مختلط برابر است با حاصل ضرب مشتق تابع خارجی نسبت به تابع داخلی ثابت و مشتق تابع داخلی.
و بلافاصله به نمودار تجزیه "کلمه به کلمه" نگاه کنید تا بفهمید چیست:

امیدوارم عبارات "مشتق" و "محصول" هیچ مشکلی ایجاد نکند. "عملکرد پیچیده" - ما قبلاً آن را مرتب کرده ایم. گیر در "مشتق یک تابع خارجی با توجه به یک تابع داخلی ثابت" است. آن چیست؟
پاسخ: این مشتق معمول تابع خارجی است که در آن فقط تابع خارجی تغییر می کند و تابع داخلی ثابت می ماند. هنوز مشخص نیست؟ خوب، بیایید از یک مثال استفاده کنیم.
اجازه دهید یک تابع \(y=\sin(x^3)\) داشته باشیم. واضح است که تابع داخلی در اینجا \(x^3\) و خارجی است  . بیایید اکنون مشتق بیرون را با توجه به باطن ثابت پیدا کنیم.
. بیایید اکنون مشتق بیرون را با توجه به باطن ثابت پیدا کنیم.
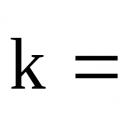 رهنمودهای ثابت سرعت واکنش برای کارهای آزمایشگاهی
رهنمودهای ثابت سرعت واکنش برای کارهای آزمایشگاهی آیا زندگی پس از مرگ وجود دارد؟
آیا زندگی پس از مرگ وجود دارد؟ دانشمندان: زمین یک "زندان فضایی" برای بشریت است دانشمندان: زمین یک زندان فضایی در جهان است
دانشمندان: زمین یک "زندان فضایی" برای بشریت است دانشمندان: زمین یک زندان فضایی در جهان است