روش بدیهی ساخت یک نظریه علمی در ریاضیات. روش اصولی ساخت نظریه علمی روش بدیهی ساخت نظریه
روش بدیهی روشی برای ساختن است نظریه ریاضیکه اساس آن بر پاره ای از احکام استوار است که بدون برهان ( بدیهیات ) پذیرفته شده اند و بقیه به صورت کاملاً منطقی از آنها گرفته شده است. با کاربرد ریشه ای این رویکرد، ریاضیات به منطق محض تقلیل می یابد، مواردی مانند شهود، نمایش های هندسی بصری، استدلال استقرایی و غیره از آن بیرون رانده می شوند. آنچه جوهر خلاقیت ریاضی است از بین می رود. پس چرا این روش اختراع شد؟ برای پاسخ به این سوال باید به ابتدای ریاضیات برگردیم.
1. بدیهیات: دو فهم
همانطور که از مدرسه به یاد داریم، برهان های ریاضی، بدیهیات و قضایا در آن ظاهر شدند یونان باستان. ساختار بدیهی هندسه در کتابی که از آن به نسلهای زیادی ریاضیات آموزش داده شد - در عناصر اقلیدس - متعارف شد. با این حال، در آن روزها مفهوم بدیهیات به گونهای متفاوت از آنچه اکنون است درک میشد. تا به حال، گاهی اوقات در کتاب های درسی مدارس می گویند بدیهیات حقایق بدیهی هستند که بدون دلیل پذیرفته می شوند. در قرن نوزدهم، این مفهوم بسیار تغییر کرد زیرا کلمه "بدیهی" ناپدید شد. بدیهیات دیگر واضح نیستند؛ آنها همچنان بدون اثبات پذیرفته می شوند، اما در اصل می توانند گزاره هایی کاملاً دلبخواه باشند. در پس این تغییر کوچک، در نگاه اول، تغییر نسبتاً بنیادی در موقعیت فلسفی وجود دارد - امتناع از شناخت تنها واقعیت ریاضی ممکن. البته نقش اصلی در این تغییر را تاریخچه پیدایش هندسه نااقلیدسی ایفا کرد که در قرن نوزدهم به لطف کار دانشمندانی مانند N.I. Lobachevsky و J. Bolyai رخ داد.
2. مسئله بدیهیات خطوط موازی
تاریخچه هندسه غیر اقلیدسی با تلاش هایی برای اثبات به اصطلاح فرض پنجم اقلیدس - اصل معروف موازی ها آغاز شد: از طریق یک نقطه خارج از یک خط، بیش از یک خط را نمی توان به موازات خط داده شده رسم کرد. این گزاره ماهیت قابل توجهی با بقیه بدیهیات اقلیدس داشت. برای بسیاری به نظر می رسید که نیاز به اثبات دارد؛ به اندازه سایر بدیهیات بدیهی نبود. این تلاشها برای قرنها موفقیتآمیز نبودند؛ بسیاری از ریاضیدانان «راهحلهای» خود را پیشنهاد کردند، که در آن ریاضیدانان دیگر بعداً خطاهایی را یافتند. (اکنون می دانیم که این تلاش ها آشکارا محکوم به شکست بودند؛ این یکی از اولین نمونه های گزاره های ریاضی غیرقابل اثبات بود).
3. هندسه لوباچفسکی
فقط در قرن 19 متوجه شد که شاید این گفته در واقع غیر قابل اثبات باشد و هندسه دیگری کاملاً متفاوت از هندسه ما وجود داشته باشد که در آن این اصل موضوع نادرست است. لوباچفسکی چه کرد؟ او کاری را انجام داد که ریاضیدانان اغلب هنگام تلاش برای اثبات یک جمله انجام می دهند. یک تکنیک مورد علاقه اثبات با تضاد است: فرض کنید که این بیانیهاشتباه. چه چیزی از این نتیجه می شود؟ برای اثبات قضیه، ریاضی دانان سعی می کنند از فرضی که انجام شده است، تناقضی استخراج کنند. اما در این مورد، لوباچفسکی بیشتر و بیشتر پیامدهای ریاضی و هندسی جدیدی را از این فرض دریافت کرد، اما آنها در یک سیستم بسیار زیبا و سازگار درونی قرار گرفتند، که با این وجود با سیستم اقلیدسی که ما به آن عادت کرده ایم متفاوت بود. دنیای جدیدی از هندسه غیراقلیدسی، بر خلاف آنچه که ما به آن عادت کردهایم، در مقابل چشمانش آشکار میشد. این امر باعث شد که لوباچفسکی متوجه شود که چنین هندسه ای امکان پذیر است. در عین حال، اصل تشابهات در هندسه لوباچفسکی به وضوح با شهود هندسی روزمره ما در تضاد بود: نه تنها از نظر شهودی آشکار نبود، بلکه از دیدگاه این شهود نیز نادرست بود.
با این حال، این یک چیز است که تصور کنیم این امر در اصل امکان پذیر است، و یک چیز دیگر است که کاملاً ریاضی ثابت کنیم که چنین سیستمی از بدیهیات برای هندسه سازگار است. این امر چندین دهه بعد در آثار دیگر ریاضیدانان - بلترامی، کلاین و پوانکاره، که مدلهایی از اصول هندسه غیراقلیدسی را در چارچوب هندسه معمولی اقلیدسی ارائه کردند، به دست آمد. آنها در واقع ثابت کردند که ناسازگاری هندسه لوباچفسکی مستلزم ناسازگاری هندسه اقلیدسی است که برای ما آشناست. برعکس آن نیز صادق است، یعنی از نظر منطق، هر دو سیستم کاملاً برابر هستند.
با این حال، یک هشدار وجود دارد که باید انجام شود. تاریخ هندسه نااقلیدسی با پدیده دیگری که بیش از یک بار در تاریخ علم مشاهده شده است به خوبی نشان داده شده است. گاهی اوقات راه حل یک مشکل نه بعد از آن، بلکه قبل از اینکه خود مشکل فرمول دقیقی را دریافت کند که برای همه به خوبی درک می شود، به وجود می آید. در این مورد چنین بود: در اواسط قرن 19 لیست کاملبدیهیات هندسه ابتدایی هنوز وجود نداشت. عناصر اقلیدس از نظر اجرای روش بدیهی به اندازه کافی سازگار نبودند. بسیاری از استدلال های اقلیدس برای شهود بصری جذاب بود؛ بدیهیات او به وضوح حتی برای صورت بندی معنادار مسئله اثبات ناپذیری فرض موازی کافی نبود. لوباچفسکی با بولیای و بلترامی با کلاین و پوانکاره در موقعیت مشابهی قرار داشتند. تنظیم مسئله اثبات ناپذیری در سطح مناسب دقت مستلزم توسعه یک دستگاه کاملاً جدید منطق ریاضی و همان روش بدیهی بود.
4. ایجاد یک روش بدیهی
این وضعیت پس از انتشار کتاب «مبانی هندسه» دی. هیلبرت درک شد؛ او مفهوم روش بدیهی را که با آن شروع کردیم، پیشنهاد کرد. هیلبرت دریافت که برای درک مبانی هندسه، لازم است همه چیز به جز منطق را کاملاً از بدیهیات حذف کرد. او این ایده را به شکل زیر بیان کرد: اعتبار بدیهیات و قضایا به هیچ وجه متزلزل نخواهد شد اگر اصطلاحات معمول «نقطه، خط، صفحه» را با عبارات دیگر، به همان اندازه متعارف، جایگزین کنیم: «صندلی، میز، لیوان آبجو»!
این هیلبرت بود که اولین سیستم منسجم و کامل بدیهیات را برای هندسه ابتدایی ساخت، این در اواخر قرن نوزدهم اتفاق افتاد. بنابراین، روش بدیهی در واقع به منظور اثبات عدم امکان اثبات برخی گزاره ها، در این مورد هندسی، ایجاد شد.
هیلبرت به کشف خود افتخار می کرد و فکر می کرد که این روش را می توان به تمام ریاضیات به طور کلی تعمیم داد: نه تنها به هندسه ابتدایی، بلکه به حساب، تجزیه و تحلیل و نظریه مجموعه ها. او "برنامه هیلبرت" را اعلام کرد که هدف آن توسعه سیستم های بدیهیات برای همه بخش های ریاضیات (و حتی بخش هایی از فیزیک) و سپس ایجاد ثبات ریاضیات با وسایل محدود بود. به محض اینکه هیلبرت به امکانات روش بدیهی پی برد، به نظر می رسید که مسیر مستقیمی برای چنین توسعه ای باز است. هیلبرت حتی یک عبارت معروف را در سال 1930 بیان کرد که به زبان روسی ترجمه شده بود مانند "ما باید بدانیم و خواهیم دانست"، به این معنی که هر چیزی که ریاضیدانان باید بدانند، دیر یا زود خواهند آموخت. این هدف اما غیرواقعی بود که خیلی بعد مشخص شد. شگفت انگیزتر از همه این است که قضیه ای که به طور موثر این امیدها را رد کرد، قضیه ناقص بودن کورت گودل، در همان کنفرانسی در سال 1930 اعلام شد که در آن هیلبرت سخنرانی معروف خود را درست یک روز قبل از این رویداد ایراد کرد.
5. امکانات روش بدیهی
روش بدیهی هیلبرت به فرد اجازه میدهد تا نظریههای ریاضی را بر روی گزارههای ریاضی کاملاً تعریفشده بسازد، که از آنها میتوان دیگران را بهطور منطقی استخراج کرد. هیلبرت در واقع فراتر رفت و تصمیم گرفت که کاهش ریاضیات به منطق ادامه یابد. همچنین می توانید این سوال را بپرسید: "آیا می توان از توضیح معنای عملیات منطقی خلاص شد؟" خود منطق را می توان از روش بدیهی حذف کرد. از نظریه های بدیهی ما به نظریه های بدیهی رسمی می رویم - اینها نظریه هایی هستند که به شکل نمادین نوشته شده اند، در حالی که ریاضیات نه تنها به دنباله ای از نتیجه گیری های منطقی، بلکه به نوعی بازی بازنویسی عبارات رسمی طبق قوانین خاص تبدیل می شود. این بازی است که اگر ساده لوحانه به آن نگاه کنید، مطلقاً معنی ندارد، مدل ریاضی دقیقی را ارائه می دهد که "اثبات" چیست. با تحلیل این بازی می توان ثابت کرد که قضایای ریاضی قابل اثبات نیستند. اما نکته اصلی: در نتیجه رسمی سازی، ریاضیدانان برای اولین بار زبان های کاملاً رسمی ساختند که منجر به ایجاد زبان های برنامه نویسی و زبان های پایگاه داده شد. توسعه مدرنفناوری رایانه در نهایت بر اساس اکتشافاتی است که در ابتدای قرن بیستم در ریاضیات انجام شد.
6. نقد روش بدیهی
بسیاری از ریاضیدانان روش بدیهی را به خاطر آنچه که برای آن ایجاد شده است مورد انتقاد قرار می دهند: این روش معنایی را از ریاضیات خارج می کند. زیرا ابتدا ریاضیات را از شر مفاهیم مختلف هندسی، از شر شهود خلاص می کنیم. با حرکت به سمت یک نظریه بدیهی رسمی، ما، به طور کلی، منطق را از ریاضیات حذف می کنیم. و در نتیجه، تنها چیزی که از برهان ماهوی باقی می ماند، اسکلتی است متشکل از نمادهای رسمی. مزیت دومی دقیقاً این است که ما نمی دانیم "معنا" و "شهود" چیست، اما دقیقاً می دانیم که دستکاری با رشته های محدود کاراکترها چیست. این به ما امکان می دهد یک مدل ریاضی دقیق از یک پدیده پیچیده - شواهد - بسازیم و آن را در معرض تجزیه و تحلیل ریاضی قرار دهیم.
اثبات ریاضی در اصل یک فرآیند روانشناختی برای متقاعد کردن مخاطب به صحت یک جمله خاص بود. در سیستم رسمی اینطور نیست: همه چیز به یک فرآیند کاملاً مکانیکی تقلیل یافته است. این فرآیند کاملاً مکانیکی را می توان توسط رایانه انجام داد. با این حال، مانند هر مدل، فرآیند مکانیکی تنها برخی از ویژگی های شواهد واقعی را منتقل می کند. این مدل محدودیت های کاربردی خود را دارد. این اشتباه است که فکر کنیم اثبات های رسمی، اثبات های ریاضی «واقعی» هستند یا اینکه ریاضیدانان در واقع در سیستم های رسمی خاصی کار می کنند.
به تفکیک آموزش ریاضی قابل ذکر است. هیچ چیز بدتر از این نیست که آموزش دانشآموزان را بر روی انجام اقدامات مکانیکی (الگوریتمها) یا ساختن نتیجهگیری منطقی رسمی قرار دهیم. به این ترتیب می توانید هر شروع خلاقانه ای را در یک فرد خراب کنید. بر این اساس، هنگام تدریس ریاضیات، نباید از موقعیت یک روش بدیهی دقیق به معنای هیلبرت به آن نزدیک شوید - این چیزی نیست که برای آن ایجاد شده است.
روش بدیهی برای اولین بار توسط اقلیدس برای ساختن هندسه ابتدایی با موفقیت استفاده شد. از آن زمان، این روش دستخوش تکامل قابل توجهی شده است و نه تنها در ریاضیات، بلکه در بسیاری از شاخههای علوم دقیق طبیعی (مکانیک، اپتیک، الکترودینامیک، نظریه نسبیت، کیهانشناسی و غیره) کاربردهای فراوانی یافته است.
توسعه و بهبود روش بدیهی در دو خط اصلی اتفاق افتاد: اول، تعمیم خود روش و دوم، توسعه تکنیکهای منطقی مورد استفاده در فرآیند استخراج قضایا از بدیهیات. برای تصور واضح تر ماهیت تغییرات رخ داده، اجازه دهید به بدیهیات اصلی اقلیدس بپردازیم. همانطور که مشخص است، مفاهیم اولیه و بدیهیات هندسه به یک روش تفسیر شده است. منظور از نقطه، خط و صفحه به عنوان مفاهیم اساسی هندسه، اشیاء فضایی آرمانی شده و خود هندسه مطالعه خصوصیات فضای فیزیکی محسوب می شود. به تدریج روشن شد که بدیهیات اقلیدس نه تنها برای توصیف خواص هندسی، بلکه سایر اشیاء ریاضی و حتی فیزیکی نیز صادق است. بنابراین، اگر منظور ما از یک نقطه، سه برابر اعداد واقعی باشد، با یک خط مستقیم یا یک صفحه - مربوطه معادلات خطی، سپس خصوصیات همه این اجسام غیر هندسی اصول هندسی اقلیدس را برآورده می کند. حتی جالب تر، تفسیر این بدیهیات با کمک اشیاء فیزیکی است، به عنوان مثال، حالت های یک سیستم مکانیکی و فیزیکوشیمیایی یا انواع احساسات رنگ. همه اینها نشان می دهد که بدیهیات هندسه را می توان با استفاده از اشیاء با ماهیت بسیار متفاوت تفسیر کرد.
این رویکرد انتزاعی به بدیهیات عمدتاً با کشف هندسه های غیر اقلیدسی توسط N.I. Lobachevsky، J. Bolyai، C. F. Gauss و B. Riemann تهیه شد. منسجم ترین بیان یک نگاه جدیددر مورد بدیهیات به عنوان اشکال انتزاعی که امکان تفاسیر مختلف را فراهم می کند، در اثر معروف دی. هیلبرت "مبانی هندسه" (1899) یافت می شود. او در این کتاب مینویسد: «ما به سه نظام مختلف از چیزها فکر میکنیم: ما چیزهای نظام اول را نقاط مینامیم و به A، B، C،... اشاره میکنیم. چیزهای نظام دوم را مستقیم می نامیم و به a، b، c،... دلالت می کنیم. ما چیزهای سیستم سوم را صفحه می نامیم و آنها را به صورت a، B، y،... تعیین می کنیم. از اینجا مشخص می شود که منظور از "نقطه"، "خط مستقیم" و "صفحه" هر سیستمی از اجسام است. فقط مهم است که خواص آنها با بدیهیات مربوطه توصیف شود. گام بعدی در مسیر انتزاع از محتوای بدیهیات با بازنمایی نمادین آنها در قالب فرمول ها و همچنین مشخص کردن دقیق آن قواعد استنتاجی مرتبط است که چگونگی فرمول های دیگر (قضیات) را از برخی فرمول ها (اصولات) توضیح می دهد. به دست آمده. در نتیجه، استدلال معنادار با مفاهیم در این مرحله از تحقیق، طبق قوانین از پیش تعیین شده به عملیاتی با فرمول تبدیل می شود. به عبارت دیگر، تفکر معنادار در اینجا در حساب دیفرانسیل و انتگرال منعکس می شود. سیستم های بدیهی از این نوع اغلب سیستم های نحوی رسمی یا حساب ها نامیده می شوند.
هر سه نوع بدیهی سازی در نظر گرفته شده در استفاده می شود علم مدرن. سیستم های بدیهی رسمی عمدتاً هنگام مطالعه مبانی منطقی یک علم خاص مورد استفاده قرار می گیرند. چنین تحقیقاتی در ارتباط با کشف پارادوکس ها در نظریه مجموعه ها بیشترین دامنه را در ریاضیات به دست آورده است. نظامهای رسمی نقش بسزایی در ایجاد زبانهای علمی خاص دارند که به کمک آنها میتوان نادرستیهای زبان معمولی و طبیعی را تا حد امکان از بین برد.
برخی از دانشمندان این نکته را تقریباً اصلی ترین نکته در فرآیند به کارگیری روش های منطقی-ریاضی در علوم خاص می دانند. بنابراین، دانشمند انگلیسی I. Woodger که یکی از پیشگامان استفاده از روش بدیهی در زیست شناسی است، معتقد است که کاربرد این روش در زیست شناسی و سایر شاخه های علوم طبیعی شامل ایجاد یک زبان علمی کامل است که در آن حساب دیفرانسیل و انتگرال ممکن است. مبنای ساخت چنین زبانی یک روش بدیهی است که در قالب یک سیستم رسمی یا حساب دیفرانسیل بیان می شود. نمادهای اولیه دو نوع به عنوان الفبای یک زبان رسمی عمل می کنند: منطقی و فردی.
نمادهای منطقی نشان دهنده ارتباطات و روابط منطقی مشترک در بسیاری یا اکثر نظریه ها هستند. نمادهای منفرد نشان دهنده موضوعات نظریه مورد مطالعه، مانند ریاضی، فیزیکی یا بیولوژیکی هستند. همانطور که دنباله خاصی از حروف الفبا یک کلمه را تشکیل می دهد، مجموعه محدودی از نمادهای مرتب شده فرمول ها و عبارات یک زبان رسمی را تشکیل می دهد. برای تمایز عبارات معنی دار یک زبان، مفهوم یک فرمول درست ساخته شده معرفی شده است. برای تکمیل فرآیند ساخت یک زبان مصنوعی، کافی است قوانین استخراج یا تبدیل یک فرمول به فرمول دیگر را به وضوح توضیح دهیم و برخی از فرمول های درست ساخته شده را به عنوان بدیهیات برجسته کنیم. بنابراین، ساخت یک زبان رسمی شده به همان شیوه ای رخ می دهد که ساختن یک سیستم بدیهی معنادار. از آنجایی که استدلال معنادار با فرمول ها در مورد اول غیرقابل قبول است، اشتقاق منطقی پیامدها در اینجا به انجام عملیات دقیقاً تجویز شده برای مدیریت نمادها و ترکیبات آنها خلاصه می شود.
هدف اصلی استفاده از زبان های رسمی در علم، تحلیل انتقادی استدلالی است که با کمک آن دانش جدیدی در علم به دست می آید. از آنجایی که زبان های رسمی منعکس کننده برخی از جنبه های استدلال معنادار هستند، می توان از آنها برای ارزیابی احتمالات خودکارسازی فعالیت های فکری نیز استفاده کرد.
سیستم های بدیهی انتزاعی بیشترین استفاده را در ریاضیات مدرن دارند که با رویکردی بسیار کلی به موضوع تحقیق مشخص می شود. ریاضیدان مدرن به جای صحبت در مورد اعداد، توابع، خطوط، سطوح، بردارها و موارد مشابه، مجموعه های مختلفی از اشیاء انتزاعی را در نظر می گیرد که ویژگی های آنها دقیقاً با استفاده از بدیهیات فرمول بندی شده است. چنین مجموعهها یا مجموعههایی، همراه با بدیهیاتی که آنها را توصیف میکنند، اکنون اغلب ساختارهای ریاضی انتزاعی نامیده میشوند.
روش بدیهی چه مزایایی برای ریاضیات خواهد داشت؟ اولاً، به طور قابل توجهی دامنه کاربرد روش های ریاضی را گسترش می دهد و اغلب فرآیند تحقیق را تسهیل می کند. هنگام مطالعه پدیده ها و فرآیندهای خاص در یک منطقه خاص، یک دانشمند می تواند از سیستم های بدیهی انتزاعی به عنوان ابزارهای آماده تحلیل استفاده کند. پس از اطمینان از اینکه پدیده های مورد بررسی اصول برخی از نظریه های ریاضی را برآورده می کنند، محقق می تواند بلافاصله از تمام قضایایی که از بدیهیات به دست می آید، بدون کار فشرده اضافی استفاده کند. رویکرد بدیهی یک متخصص در یک علم خاص را از انجام تحقیقات ریاضی نسبتاً پیچیده و دشوار نجات می دهد.
برای یک ریاضیدان، این روش درک بهتر موضوع تحقیق، برجسته کردن جهت های اصلی در آن و درک وحدت و پیوند روش ها و نظریه های مختلف را ممکن می سازد. وحدتی که به کمک روش بدیهی به تعبیر مجازی ن. بوربکی حاصل می شود، وحدتی نیست که «اسکلتی خالی از حیات می دهد. این شیره مغذی بدن در حال رشد کامل، یک ابزار تحقیقاتی چکش خوار و پربار است...» به لطف روش بدیهی، به ویژه در شکل رسمی آن، آشکار ساختن ساختار منطقی به طور کامل امکان پذیر می شود. نظریه های مختلف. در کامل ترین شکل خود، این امر در مورد نظریه های ریاضی صدق می کند. در دانش علوم طبیعی باید خود را به بدیهی سازی هسته اصلی نظریه ها محدود کنیم. علاوه بر این، استفاده از روش بدیهی این امکان را فراهم می کند که مسیر استدلال خود را بهتر کنترل کنیم و به دقت منطقی لازم دست یابیم. با این حال ارزش اصلیبدیهی سازی، به ویژه در ریاضیات، این است که به عنوان روشی برای مطالعه الگوهای جدید، برقراری ارتباط بین مفاهیم و نظریه هایی که قبلاً از یکدیگر جدا به نظر می رسید، عمل می کند.
استفاده محدود از روش بدیهی در علوم طبیعی در درجه اول با این واقعیت توضیح داده می شود که نظریه های آن باید دائماً توسط تجربه کنترل شوند.
به همین دلیل، نظریه علوم طبیعی هرگز برای کامل شدن و انزوا کامل تلاش نمی کند. در همین حال، در ریاضیات ترجیح می دهند با سیستم هایی از بدیهیات سروکار داشته باشند که شرط کامل بودن را برآورده می کنند. اما همانطور که K. Godel نشان داد، هر سیستم منسجمی از بدیهیات با ماهیت غیر پیش پا افتاده نمی تواند کامل باشد.
لازمه سازگاری یک سیستم بدیهیات بسیار مهمتر از الزام کامل بودن آنهاست. اگر نظام بدیهیات متناقض باشد، برای دانش ارزشی نخواهد داشت. با محدود کردن خود به سیستمهای ناقص، میتوانیم به طور طبیعی فقط محتوای اصلی را بدیهی کنیم نظریه های علمی، امکان توسعه و اصلاح بیشتر نظریه را با آزمایش فراهم می کند. حتی چنین هدف محدودی در تعدادی از موارد بسیار مفید است، به عنوان مثال، برای کشف برخی مقدمات و مفروضات ضمنی نظریه، نظارت بر نتایج بهدستآمده، نظامبندی آنها و غیره.
امیدوارکننده ترین کاربرد روش بدیهی در علومی است که مفاهیم مورد استفاده از ثبات قابل توجهی برخوردارند و می توان از تغییر و توسعه آنها انتزاع گرفت.
در چنین شرایطی است که می توان ارتباطات صوری-منطقی بین اجزای مختلف نظریه را شناسایی کرد. بنابراین، روش بدیهی، تا حد بیشتری از روش فرضی-قیاسی، برای مطالعه دانش آماده و به دست آمده اقتباس شده است.
تحلیل پیدایش دانش و روند شکل گیری آن مستلزم روی آوردن به دیالکتیک ماتریالیستی به عنوان عمیق ترین و جامع ترین دکترین توسعه است.
روش بدیهی ساخت یک نظریه علمی در ریاضیات
روش بدیهی در یونان باستان ظاهر شد و اکنون در تمام علوم نظری، عمدتاً در ریاضیات استفاده می شود.
روش بدیهی ساخت یک نظریه علمی به شرح زیر است: مفاهیم اساسی شناسایی می شوند، بدیهیات نظریه تدوین می شوند و سایر گزاره ها بر اساس آنها به صورت منطقی استنتاج می شوند.
مفاهیم اصلی به شرح زیر برجسته شده است. مشخص است که یک مفهوم باید با کمک مفاهیم دیگر توضیح داده شود که به نوبه خود با کمک برخی از مفاهیم شناخته شده نیز تعریف می شوند. بنابراین به مفاهیم ابتدایی می رسیم که از طریق دیگران قابل تعریف نیستند. این مفاهیم پایه نامیده می شوند.
وقتی یک گزاره، یک قضیه را اثبات می کنیم، بر مقدماتی تکیه می کنیم که قبلاً اثبات شده در نظر گرفته می شوند. اما این مقدمات هم ثابت شد؛ باید توجیه میشد. در نهایت به جملات غیر قابل اثبات می رسیم و آنها را بدون دلیل می پذیریم. این گزاره ها بدیهیات نامیده می شوند. مجموعه بدیهیات باید به گونه ای باشد که بر اساس آن بتوان گزاره های بعدی را اثبات کرد.
پس از شناسایی مفاهیم اساسی و فرمول بندی بدیهیات، قضایا و سایر مفاهیم را به روشی منطقی استخراج می کنیم. این ساختار منطقی هندسه است. بدیهیات و مفاهیم اساسی پایه های پلان سنجی را تشکیل می دهند.
از آنجایی که ارائه یک تعریف واحد از مفاهیم اساسی برای همه هندسه ها غیرممکن است، مفاهیم اساسی هندسه باید به عنوان اشیایی از هر ماهیتی تعریف شوند که بدیهیات این هندسه را برآورده کنند. بنابراین، در ساخت بدیهی یک سیستم هندسی، از یک سیستم خاص از بدیهیات یا بدیهیات شروع می کنیم. این بدیهیات خصوصیات مفاهیم اساسی سیستم هندسی را توصیف می کنند و ما می توانیم مفاهیم اساسی را در قالب اشیایی با هر ماهیتی که دارای ویژگی های مشخص شده در بدیهیات هستند نشان دهیم.
پس از صورت بندی و اثبات اولین گزاره های هندسی، اثبات برخی گزاره ها (قضیه ها) با کمک برخی دیگر ممکن می شود. اثبات بسیاری از قضایا به فیثاغورث و دموکریتوس نسبت داده شده است.
به بقراط خیوسی، اولین دوره نظام مند هندسه بر اساس تعاریف و بدیهیات را تدوین کرد. این دوره و درمان های بعدی آن «عناصر» نام داشت.
سپس در قرن سوم. پیش از میلاد، کتابی از اقلیدس با همین نام در اسکندریه در ترجمه روسی "آغاز" ظاهر شد. اصطلاح "هندسه ابتدایی" از نام لاتین "شروع" گرفته شده است. علیرغم اینکه آثار پیشینیان اقلیدس به دست ما نرسیده است، می توان بر اساس عناصر اقلیدس در مورد این آثار نظری داد. در "اصول" بخش هایی وجود دارد که از نظر منطقی ارتباط بسیار کمی با بخش های دیگر دارند. ظاهر آنها را فقط می توان با این واقعیت توضیح داد که آنها طبق سنت معرفی شدند و از "عناصر" پیشینیان اقلیدس کپی کردند.
عناصر اقلیدس از 13 کتاب تشکیل شده است. کتاب های 1 تا 6 به پلان سنجی اختصاص دارد، کتاب های 7 تا 10 در مورد کمیت های حسابی و غیرقابل قیاس است که می توان با استفاده از قطب نما و خط کش ساخت. کتاب های 11 تا 13 به استریومتری اختصاص داشت.
Principia با ارائه 23 تعریف و 10 بدیهیات آغاز می شود. پنج بدیهیات اول «مفاهیم کلی» هستند، بقیه «مقامات» نامیده می شوند. دو اصل اول اعمال را با استفاده از یک خط کش ایده آل تعیین می کنند، سوم - با استفاده از یک قطب نما ایده آل. چهارمین عبارت «همه زوایای قائمه با یکدیگر برابرند» زائد است، زیرا میتوان آن را از بدیهیات باقیمانده استنتاج کرد. فرضیه آخر پنجم می گوید: «اگر یک خط مستقیم بر روی دو خط مستقیم بیفتد و زوایای یک طرفه داخلی را با مجموع کمتر از دو خط مستقیم تشکیل دهد، در این صورت با امتداد نامحدود این دو خط مستقیم، آنها بر روی یکدیگر تلاقی می کنند. سمتی که زاویه آن کمتر از دو خط مستقیم است.»
پنج " مفاهیم کلی"اصول اقلیدسی اندازه گیری طول، زاویه، مساحت، حجم: "برابر با یکدیگر برابرند"، "اگر مساوی به مساوی اضافه شود، مجموع برابر است"، "اگر مساوی از مساوی کم شود، باقیمانده برابر است" «آنهایی که با یکدیگر ترکیب شده اند با یکدیگر برابرند»، «کل بزرگتر از جزء است».
سپس انتقاد از هندسه اقلیدس آغاز شد. اقلیدس به سه دلیل مورد انتقاد قرار گرفت: زیرا او فقط کمیت های هندسی را در نظر گرفت که می توان با استفاده از قطب نما و خط کش ساخت. برای این واقعیت که او هندسه و حساب را از هم جدا کرد و برای اعداد صحیح آنچه را قبلاً برای کمیت های هندسی ثابت کرده بود، و در نهایت، برای بدیهیات اقلیدس ثابت کرد. به شدت مورد انتقاد قرار گرفت پنجمین اصل پیچیده اقلیدس بود. بسیاری آن را زائد می دانستند و اینکه می توان و باید از بدیهیات دیگر استنباط کرد. برخی دیگر معتقد بودند که باید با یک خط ساده تر و واضح تر، معادل آن جایگزین شود: "از طریق نقطه ای خارج از یک خط، بیش از یک خط مستقیم نمی توان در صفحه آنها رسم کرد که خط داده شده را قطع نمی کند."
انتقاد از شکاف بین هندسه و حساب منجر به گسترش مفهوم عدد به عدد واقعی. اختلافات در مورد فرض پنجم منجر به این واقعیت شد که در آغاز قرن نوزدهم N.I. Lobaczewski، J. Bolyai و K.F. گاوس هندسه جدیدی ساخت که در آن تمام بدیهیات هندسه اقلیدس به استثنای فرض پنجم برآورده شد. با عبارت مخالف جایگزین شد: "در یک صفحه، از طریق نقطه ای خارج از یک خط، بیش از یک خط می توان رسم کرد که خط داده شده را قطع نمی کند." این هندسه به اندازه هندسه اقلیدس سازگار بود.
مدل پلان سنجی لوباچفسکی در صفحه اقلیدسی توسط ریاضیدان فرانسوی هنری پوانکاره در سال 1882 ساخته شد.
بیایید یک خط افقی روی صفحه اقلیدسی رسم کنیم (شکل 1 را ببینید). این خط مطلق (x) نامیده می شود. نقاط صفحه اقلیدسی که بالای مطلق قرار دارند، نقاطی از صفحه لوباچفسکی هستند. هواپیمای لوباچفسکی یک نیمه صفحه باز است که بالای مطلق قرار دارد. پاره های غیر اقلیدسی در مدل پوانکاره کمان هایی از دایره هستند که در مرکز مطلق یا پاره های خطوط مستقیم عمود بر مطلق (AB، CD) قرار دارند. یک شکل در صفحه لوباچفسکی شکل یک نیمه صفحه باز است که بالای مطلق (F) قرار دارد. حرکت نااقلیدسی ترکیبی از تعداد محدودی از وارونگی ها است که بر تقارن مطلق و محوری متمرکز شده اند که محورهای آنها عمود بر مطلق است. دو بخش غیر اقلیدسی مساوی هستند اگر بتوان یکی از آنها را با یک حرکت غیراقلیدسی به دیگری منتقل کرد. اینها مفاهیم اساسی بدیهیات پلان سنجی لوباچفسکی هستند.
همه بدیهیات پلان سنجی لوباچفسکی سازگار هستند. تعریف خط مستقیم به این صورت است: «خط مستقیم غیر اقلیدسی، نیم دایره ای است که انتهای آن در مطلق یا پرتویی است که ابتدای آن در مطلق و عمود بر مطلق است». بنابراین، بیان بدیهیات موازی لوباچفسکی نه تنها برای برخی از خطوط a و نقطه A که روی این خط قرار ندارند، بلکه برای هر خط a و هر نقطه A که روی آن قرار ندارد نیز برآورده می شود (شکل 2 را ببینید).
پس از هندسه لوباچفسکی، هندسه های ثابت دیگری به وجود آمد: هندسه تصویری جدا از اقلیدسی، هندسه اقلیدسی چند بعدی پدید آمد، هندسه ریمانی (نظریه کلی فضاها با قانون دلخواه برای اندازه گیری طول ها) و غیره. فضای اقلیدسی، هندسه برای 40 - 50 سال به مجموعه ای از نظریه های مختلف تبدیل شده است، که فقط تا حدودی شبیه به جد خود - هندسه اقلیدسی است. 60,896.
از این روش برای ساختن نظریه های ریاضیات و علوم دقیق استفاده می شود. مزایای این روش در قرن سوم توسط اقلیدس در هنگام ساختن یک سیستم دانش در مورد هندسه ابتدایی درک شد. در ساخت بدیهی نظریه ها، حداقل تعداد مفاهیم و گزاره های اولیه دقیقاً از بقیه متمایز می شوند. یک نظریه بدیهی به عنوان یک سیستم علمی درک می شود که تمام مفاد آن به طور منطقی محض از مجموعه ای از مقررات پذیرفته شده در این سیستم بدون اثبات و بدیهیات نامیده می شود و همه مفاهیم به طبقه ثابت معینی از مفاهیم به نام غیر قابل تعریف تقلیل می یابد. این نظریه در صورتی تعریف می شود که نظام بدیهیات و مجموعه ابزارهای منطقی مورد استفاده - قواعد استنتاج - مشخص شود. مفاهیم مشتق شده در نظریه بدیهیات مخفف ترکیبی از مفاهیم اساسی هستند. قابل قبول بودن ترکیب ها با بدیهیات و قواعد استنتاج تعیین می شود. به عبارت دیگر، تعاریف در نظریه های بدیهی، اسمی هستند.
بدیهیات باید از نظر منطقی قوی تر از سایر گزاره هایی باشد که به عنوان پیامدها از آن به دست می آیند. نظام بدیهیات یک نظریه به طور بالقوه شامل همه پیامدها یا قضایایی است که می توان با کمک آنها اثبات کرد. بنابراین، تمام محتوای اساسی نظریه در آن متمرکز شده است. بسته به ماهیت بدیهیات و ابزار استنتاج منطقی، موارد زیر متمایز می شوند:
- 1) سیستم های بدیهی رسمی، که در آنها بدیهیات فرمول های اولیه هستند و قضایا طبق قوانین تبدیل معین و دقیق فهرست شده از آنها به دست می آیند که در نتیجه ساخت یک سیستم به نوعی دستکاری با فرمول ها تبدیل می شود. توسل به چنین سیستم هایی برای ارائه مقدمات اولیه تئوری و ابزار منطقی نتیجه گیری تا حد امکان ضروری است. بدیهیات شکست تلاش های لوباچفسکی برای اثبات بدیهیات موازی اقلیدس او را به این باور رساند که هندسه دیگری امکان پذیر است. اگر آموزه بدیهیات و منطق ریاضی در آن زمان وجود داشت، میتوانست به راحتی از اثبات اشتباه اجتناب شود.
- 2) سیستم های بدیهی نیمه رسمی یا انتزاعی که در آنها ابزارهای استنتاج منطقی در نظر گرفته نمی شوند، بلکه شناخته شده فرض می شوند و خود بدیهیات اگرچه تفسیرهای زیادی را مجاز می کنند، اما به عنوان فرمول عمل نمی کنند. چنین سیستم هایی معمولاً در ریاضیات مطرح می شوند.
- 3) سیستم های بدیهی معنادار یک تفسیر واحد را فرض می کنند و ابزار استنتاج منطقی شناخته شده است. برای نظام مند کردن دانش علمی در علوم طبیعی دقیق و سایر علوم تجربی توسعه یافته استفاده می شود.
تفاوت قابل توجه بدیهیات ریاضی و تجربی نیز این است که از ثبات نسبی برخوردارند، در حالی که در نظریه های تجربی با کشف نتایج مهم جدید تحقیقات تجربی، محتوای آنها تغییر می کند. با آنها است که ما دائماً باید هنگام توسعه نظریه ها در نظر بگیریم، بنابراین سیستم های بدیهی در چنین علومی هرگز نمی توانند برای اشتقاق کامل یا بسته باشند.
روش بدیهی یکی از روش های ساخت قیاسی نظریه های علمی است که در آن:
1. مجموعه معینی از گزاره های یک نظریه خاص (اصولات) که بدون اثبات پذیرفته شده اند انتخاب می شود.
2. مفاهیم موجود در آنها به وضوح در چارچوب این نظریه تعریف نشده است.
3. قواعد تعریف و قواعد برای انتخاب یک نظریه معین ثابت است و به فرد امکان می دهد اصطلاحات (مفاهیم) جدیدی را وارد نظریه کند و به طور منطقی برخی از پیشنهادات را از دیگران استنباط کند.
4. تمام گزاره های دیگر این نظریه (قضیه) از 1 بر اساس 3 مشتق شده اند.
در ریاضیات، AM از آثار هندسهدانان یونان باستان سرچشمه میگیرد. درخشان، که تا قرن 19 تنها باقی مانده است. مدل استفاده از AM هندسی بود. سیستم معروف به "آغاز" اقلیدس (حدود 300 قبل از میلاد). اگر چه در آن زمان هنوز مسئله توصیف منطق مطرح نشده بود. ابزاری که برای استخراج پیامدهای معنیدار از بدیهیات استفاده میشود، در سیستم اقلیدسی ایده دستیابی به کل محتوای اساسی هندسه در حال حاضر کاملاً واضح است. نظریه ها با روشی کاملاً قیاسی از تعداد معین و نسبتاً کمی از گزاره ها - بدیهیات که صدق آنها به وضوح آشکار به نظر می رسید.
باز شدن در ابتدا قرن 19 هندسه غیر اقلیدسی توسط N.I. Lobachevsky و J. Bolyai انگیزه ای برای توسعه بیشتر AM بود. آنها ثابت کردند که با جایگزینی معمول و به نظر می رسد، تنها فرضیه V "عینی واقعی" اقلیدس در مورد تشابهات با نفی آن، شما می توانید کاملا منطقی توسعه دهید. توسط هندسی نظریه ای به اندازه هندسه اقلیدس هماهنگ و سرشار از محتوا. این واقعیت ریاضیدانان قرن نوزدهم را مجبور کرد. به روش قیاسی ساخت ریاضی توجه ویژه ای داشته باشید. تئوری هایی که منجر به پیدایش مسائل جدید مرتبط با مفهوم ریاضیات ریاضی و ریاضیات رسمی (بدیهی) شد. نظریه ها. همانطور که تجربه بدیهی انباشته شد. ارائه ریاضی نظریه ها - در اینجا لازم است قبل از هر چیز به تکمیل یک ساختار منطقی بی عیب و نقص (برخلاف عناصر اقلیدس) از هندسه ابتدایی توجه شود [M. پاش (M. Pasch)، J. Peano (G. Peano)، D. Hilbert (D. Hilbert)] و اولین تلاش ها برای بدیهی سازی حساب (J. Peano)، - مفهوم بدیهیات رسمی روشن شد. سیستم ها (به زیر مراجعه کنید)؛ یک ویژگی خاص بوجود آمد. مشکلاتی که بر اساس آن به اصطلاح نظریه شواهدبه عنوان بخش اصلی ریاضیات مدرن. منطق.
درک نیاز به اثبات ریاضیات و تکالیف خاص در این زمینه به شکلی کم و بیش واضح در قرن نوزدهم پدیدار شد. در عین حال، از یک سو، شفاف سازی مفاهیم اساسی و تقلیل مفاهیم پیچیده تر به ساده ترین ها بر مبنای دقیق و منطقی هر چه بیشتر توسط چ. arr در زمینه تحلیل [A. Cauchy، مفاهیم کارکردی-نظری B. Bolzano و K. Weierstrass، پیوستار G. Cantor و R. Dedekind (R. Dedekind)]; از سوی دیگر، کشف هندسههای غیر اقلیدسی باعث توسعه ریاضیات ریاضی، ظهور ایدههای جدید و فرمولبندی مسائل فراریاضیات عمومیتر شد. شخصیت، اول از همه، مشکلات مرتبط با مفهوم بدیهی دلخواه است. تئوری هایی مانند مشکلات سازگاری، کامل بودن و استقلال یک سیستم خاص از بدیهیات. اولین نتایج در این زمینه با روش تفسیر به دست آمد که تقریباً می توان آن را به شرح زیر توصیف کرد. اجازه دهید هر مفهوم اولیه و رابطه یک بدیهیات معین. تئوری T با یک نظریه خاص ریاضی مطابقت دارد. یک شی مجموعه چنین اشیایی نامیده می شود. حوزه تفسیر اکنون هر گزاره نظریه T به طور طبیعی با یک گزاره خاص در مورد عناصر حوزه تفسیر مرتبط است که می تواند درست یا نادرست باشد. سپس گزاره نظریه T تحت آن تفسیر به ترتیب درست یا نادرست گفته می شود. حوزه تفسیر و ویژگیهای آن معمولاً موضوع بررسی یک نظریه ریاضی است، به طور کلی نظریه دیگری، ریاضی. نظریه T 1، به ویژه، همچنین می تواند بدیهی باشد. روش تفسیر به ما امکان می دهد واقعیت سازگاری نسبی را به روش زیر ثابت کنیم، یعنی گزاره هایی مانند: "اگر نظریه T 1 سازگار است، نظریه T نیز سازگار است." بگذارید نظریه T در نظریه T 1 به گونه ای تفسیر شود که همه بدیهیات نظریه T توسط قضاوت های واقعی نظریه T 1 تفسیر شوند. سپس هر قضیه نظریه T، یعنی هر گزاره A که به طور منطقی از بدیهیات در T استنباط می شود، در T 1 با گزاره خاصی که در T 1 از تفاسیر بدیهیات استنتاج شده است تفسیر می شود. من،و بنابراین درست است. آخرین بیانیه مبتنی بر فرض دیگری است که ما به طور ضمنی از شباهت معین منطقی میسازیم. میانگین تئوری های T و T 1 است، اما در عمل معمولا این شرط برقرار است. (در آغاز به کارگیری روش تفسیر، حتی به طور خاص به این فرض فکر نمی شد: آن را بدیهی تلقی می کردند؛ در واقع، در مورد آزمایش های اول، براهین قضایای مربوط به سازگاری نسبی منطقی بود. ابزار تئوری های T و T 1 به سادگی منطبق بودند - این منطق کلاسیک محمولات بود.) حال بگذارید نظریه T متناقض باشد، یعنی می توان برخی از ادعاهای A این نظریه را همراه با نفی آن در آن استنتاج کرد. سپس از موارد فوق چنین استنباط می شود که گزاره ها و در عین حال گزاره های درست نظریه T 1 خواهند بود، یعنی نظریه T 1 متناقض است. برای مثال، این روش ثابت شد [F. Klein (F. Klein), A. Poincare (N. Poincare)] سازگاری هندسه Lobachevsky غیر اقلیدسی با این فرض که هندسه اقلیدسی سازگار است. و پرسش از قوام بدیهیات هیلبرت هندسه اقلیدسی (D. Hilbert) به مسئله ثبات حساب تقلیل یافت. روش تفسیر همچنین به ما اجازه می دهد تا مسئله استقلال سیستم های بدیهیات را حل کنیم: ثابت کنیم که اصل نظریه T به سایر بدیهیات این نظریه بستگی ندارد، یعنی از آنها قابل استنتاج نیست، و بنابراین، برای دستیابی به کل دامنه این نظریه ضروری است، کافی است چنین تفسیری از نظریه T بسازید که در آن اصل ابیل نادرست باشد و سایر بدیهیات این نظریه صادق باشند. شکل دیگر این روش اثبات استقلال، ایجاد ثبات نظریه است که در صورتی به دست می آید که در یک نظریه معین، TaxiomA با نفی آن جایگزین شود. تقلیل فوق الذکر مسئله سازگاری هندسه لوباچفسکی به مسئله قوام هندسه اقلیدسی، و این دومی - به مسئله قوام حساب، نتیجه آن این است که فرض اقلیدس از آن قابل استنتاج نیست. بدیهیات دیگر هندسه، مگر اینکه حساب سازگار باشد اعداد طبیعی. ضعف روش تفسیری این است که در مسائل قوام و استقلال نظام های بدیهی، دستیابی به نتایجی را ممکن می سازد که به ناچار فقط ماهیت نسبی دارند. اما دستاورد مهم این روش این واقعیت بود که با کمک آن نقش ویژه حساب به عنوان یک علم ریاضی بر اساس نسبتاً دقیق آشکار شد. در نظریهها، سؤال مشابهی برای تعدادی دیگر از نظریهها به مسئله سازگاری تقلیل مییابد.
پیشرفتهای بعدی- و به تعبیری این اوج بود - AM در آثار دی. هیلبرت و مکتب او در قالب به اصطلاح دریافت کرد. روش فرمالیسمدر مبانی ریاضیات در چارچوب این جهت، مرحله بعدی شفاف سازی مفهوم بدیهیات توسعه یافت. نظریه ها، یعنی مفهوم سیستم رسمیدر نتیجه این شفاف سازی، نمایش خود ریاضیات ممکن شد. نظریه ها به عنوان ریاضیات دقیق اشیاء و ساختن یک نظریه کلی، یا فرا نظریه،چنین نظریه هایی در همان زمان، چشم انداز وسوسه انگیز به نظر می رسید (و دی. هیلبرت زمانی مجذوب آن بود) برای حل تمام سؤالات اصلی پایه ریاضیات در این مسیر. مفهوم اصلی این جهت، مفهوم نظام رسمی است. هر سیستم رسمی به عنوان یک کلاس دقیقاً تعریف شده از عبارات ساخته می شود - فرمول ها، که در آن یک زیر کلاس از فرمول ها به نام فرمول ها به روشی دقیق مشخص می شود. قضایای این نظام صوری در عین حال، فرمولهای یک سیستم رسمی مستقیماً معنای معنیداری ندارند و میتوانند از نمادهای دلخواه، به طور کلی، یا نمادهای ابتدایی ساخته شوند، که تنها با ملاحظات راحتی فنی هدایت میشوند. در واقع، روش ساخت فرمول ها و مفهوم یک قضیه یک سیستم صوری خاص به گونه ای انتخاب شده است که می توان از کل این دستگاه صوری برای بیان، شاید به اندازه کافی و کامل تر، یک ریاضی خاص (و غیر ریاضی) استفاده کرد. ) نظریه، به طور دقیق تر، به عنوان واقعی آن محتوا و ساختار قیاسی آن طرح کلی برای ساخت (تعیین) یک سیستم رسمی دلخواه S به شرح زیر است.
I. زبان سیستم اس:
الف) الفبا - لیستی از نمادهای ابتدایی سیستم؛
ب) قواعد شکل گیری ( نحو) - قوانینی که طبق آنها فرمول های سیستم S از نمادهای ابتدایی ساخته می شوند؛ در این حالت، دنباله ای از نمادهای ابتدایی فرمول در نظر گرفته می شود اگر و تنها در صورتی که بتوان آن را با استفاده از قوانین تشکیل ساخت. .
II. بدیهیات سیستم S. مجموعه خاصی از فرمول ها (معمولاً محدود یا قابل شمارش) شناسایی می شود که نامیده می شوند. بدیهیات سیستم اس.
III. قوانین برداشت سیستم اس.مجموعه ای (معمولاً متناهی) از محمولات روی مجموعه تمام فرمول های سیستم ثابت می شود اس.اجازه دهید - k.-l. از این محمولات، اگر گزاره برای این فرمول ها صادق باشد، می گویند که فرمول طبق قاعده مستقیماً از فرمول ها پیروی می کند.
7. نظریه احتمال:
نظریه احتمال –یک علم ریاضی که الگوها را در پدیده های تصادفی مطالعه می کند. یکی از مفاهیم اساسی نظریه احتمال، مفهوم است رویداد تصادفی (یا به سادگی مناسبت ها ).
رویدادهر واقعیتی است که ممکن است در نتیجه تجربه اتفاق بیفتد یا نباشد. نمونه هایی از رویدادهای تصادفی: افتادن شش عدد هنگام پرتاب تاس، خرابی یک دستگاه فنی، تحریف پیام هنگام انتقال آن از طریق یک کانال ارتباطی. برخی از رویدادها با شماره ، مشخص کردن درجه امکان عینی وقوع این حوادث، نامیده می شود احتمالات وقایع .
چندین رویکرد برای مفهوم "احتمال" وجود دارد.
ساخت مدرن نظریه احتمال بر اساس رویکرد بدیهی و مبتنی بر مفاهیم ابتدایی نظریه مجموعه ها است. این رویکرد نظریه مجموعه نامیده می شود.
اجازه دهید آزمایشی با یک نتیجه تصادفی انجام شود. مجموعه W را از تمام نتایج ممکن آزمایش در نظر بگیرید. هر یک از عناصر آن را می نامیم رویداد ابتداییو مجموعه Ω است فضای رویدادهای ابتدایی. هر رویدادی آدر تفسیر نظری مجموعه، زیرمجموعه خاصی از مجموعه Ω وجود دارد: .
قابل اعتمادرویداد W نامیده می شود که در هر آزمایش رخ می دهد.
غیر ممکنرویداد Æ نامیده می شود که نمی تواند در نتیجه آزمایش رخ دهد.
ناسازگاررویدادهایی هستند که نمی توانند به طور همزمان در یک تجربه رخ دهند.
میزان(ترکیب) دو رویداد آو ب(نشان داده شده است آ+ب, آÈ ب) رویدادی است که شامل این واقعیت است که حداقل یکی از رویدادها رخ می دهد، یعنی. آیا ب، یا هر دو به طور همزمان.
کار(تقاطع) دو رویداد آو ب(نشان داده شده است آ× ب, آÇ ب) رویدادی است که در آن هر دو رویداد رخ می دهد آو ببا یکدیگر.
در مقابلبه رویداد آچنین رویدادی نامیده می شود که آن رویداد است آاتفاق نمی افتد.
مناسبت ها A k(ک=1, 2, …, n) فرم گروه کامل در صورتی که به صورت زوجی ناسازگار باشند و در مجموع یک رویداد قابل اعتماد را تشکیل دهند.
احتمال وقوع رویدادآآنها نسبت تعداد پیامدهای مطلوب برای این رویداد را به تعداد کل همه پیامدهای ابتدایی ناسازگار به همان اندازه ممکن که گروه کامل را تشکیل می دهند، می گویند. بنابراین، احتمال رویداد A با فرمول تعیین می شود
که در آن m تعداد پیامدهای ابتدایی مطلوب A است. n تعداد تمام نتایج آزمون ابتدایی ممکن است.
در اینجا فرض بر این است که نتایج ابتدایی ناسازگار هستند، به همان اندازه ممکن هستند و یک گروه کامل را تشکیل می دهند. ویژگی های زیر از تعریف احتمال به دست می آید:
مقاله خودش 1. احتمال یک رویداد قابل اعتماد برابر با یک است.در واقع، اگر رویداد قابل اعتماد باشد، هر نتیجه اولیه آزمون به نفع رویداد است. در این مورد m = n، بنابراین،
P (A) = m / n = n / n = 1.
S در حدود با t در حدود 2. احتمال یک رویداد غیرممکن صفر است.در واقع، اگر رویدادی غیرممکن باشد، هیچ یک از نتایج اولیه آزمون به نفع رویداد نیست. در این مورد m = 0، بنابراین،
P (A) = m / n = 0 / n = 0.
با در حدود با t در حدود 3. احتمال یک رویداد تصادفی عددی مثبت بین صفر و یک استدر واقع، یک رویداد تصادفی تنها به نفع بخشی از تعداد کلنتایج آزمون ابتدایی در این مورد 0< m < n, значит, 0 < m / n < 1, следовательно,
0 <Р (А) < 1
بنابراین، احتمال هر رویدادی نابرابری مضاعف را ارضا می کند
 دانشگاه صنعتی و مدیریت دولتی مسکو
دانشگاه صنعتی و مدیریت دولتی مسکو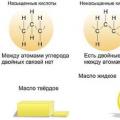 لیپیدها و نقش آنها زیست شناسی در دبیرستان
لیپیدها و نقش آنها زیست شناسی در دبیرستان