همچنین مشکلاتی برای شما پیش خواهد آمد که خودتان آنها را حل کنید که می توانید پاسخ آنها را ببینید.

انتگرال را می توان از حاصل ضرب توابع مثلثاتی به مجموع تبدیل کرد

اجازه دهید انتگرال هایی را در نظر بگیریم که در آنها انتگرال حاصل ضرب سینوس ها و کسینوس های درجه اول x در عوامل مختلف است، یعنی انتگرال های شکل

استفاده از فرمول های معروف مثلثاتی

(2)
(3)
(4)
می توان هر یک از محصولات را در انتگرال های شکل (31) به یک جمع جبری تبدیل کرد و طبق فرمول ها ادغام کرد.

(5)

(6)

مثال 1.پیدا کنید

راه حل. طبق فرمول (2) در

مثال 2.پیدا کنید انتگرال یک تابع مثلثاتی

راه حل. طبق فرمول (3) در

مثال 3.پیدا کنید انتگرال یک تابع مثلثاتی

راه حل. طبق فرمول (4) در تبدیل زیر انتگرال را بدست می آوریم:

با استفاده از فرمول (6) بدست می آوریم

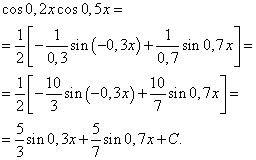
انتگرال حاصل ضرب توان های سینوس و کسینوس همان برهان

حال اجازه دهید انتگرال هایی از توابع را در نظر بگیریم که حاصل ضرب قدرت های سینوس و کسینوس همان آرگومان هستند، یعنی.

(7)

در موارد خاص، یکی از شاخص های ( متریا n) ممکن است صفر باشد.

هنگام ادغام چنین توابعی، از آن استفاده می شود که توان زوج کسینوس را می توان از طریق سینوس بیان کرد و دیفرانسیل سینوس برابر با cos است. x dx(یا حتی توان سینوس را می توان بر حسب کسینوس بیان کرد و دیفرانسیل کسینوس برابر است با - sin x dx ) .

دو مورد باید از هم تفکیک شود: 1) حداقل یکی از شاخص ها مترو nعجیب و غریب 2) هر دو شاخص زوج هستند.

بگذارید اولین مورد، یعنی نشانگر اتفاق بیفتد n = 2ک+ 1 - عجیب و غریب. سپس، با توجه به آن

انتگرال به گونه ای ارائه می شود که یک قسمت آن تابعی از سینوس و دیگری دیفرانسیل سینوس است. اکنون از جایگزینی متغیر استفاده می کنیم تی= گناه xراه حل به ادغام چند جمله ای با توجه به کاهش می یابد تی. اگر فقط مدرک مترعجیب است، سپس آنها همین کار را می کنند و عامل گناه را جدا می کنند x، بقیه انتگرال را بر حسب cos بیان می کند xو ایمان داشتن تی= cos x. این تکنیک همچنین می تواند مورد استفاده قرار گیرد زمانی که ادغام قدرت های نسبی سینوس و کسینوس ، وقتی حداقل یکی از شاخص ها عجیب و غریب است . تمام نکته این است ضریب توانهای سینوس و کسینوس یک مورد خاص از محصول آنهاست : وقتی یک تابع مثلثاتی در مخرج یک انتگرال باشد، درجه آن منفی است. اما مواردی از توابع مثلثاتی جزئی نیز وجود دارد که توان آنها فقط زوج است. درباره آنها - در پاراگراف بعدی.

اگر هر دو شاخص مترو n- حتی، سپس، با استفاده از فرمول های مثلثاتی

نماهای سینوس و کسینوس را کاهش دهید، پس از آن انتگرالی از همان نوع بالا به دست می آید. بنابراین، ادغام باید طبق همان طرح ادامه یابد. اگر یکی از نماهای زوج منفی باشد، یعنی ضریب توان های زوج سینوس و کسینوس در نظر گرفته شود، این طرح مناسب نیست. . سپس بسته به نحوه تبدیل انتگرال از تغییر متغیر استفاده می شود. چنین موردی در پاراگراف بعدی بررسی خواهد شد.

مثال 4.پیدا کنید انتگرال یک تابع مثلثاتی

راه حل. توان کسینوس فرد است. بنابراین، بیایید تصور کنیم

تی= گناه x(سپس dt= cos x dx ). سپس می گیریم

با بازگشت به متغیر قدیمی، بالاخره پیدا می کنیم

مثال 5.پیدا کنید انتگرال یک تابع مثلثاتی

.

راه حل. نما کسینوس، مانند مثال قبلی، فرد است، اما بزرگتر است. بیایید تصور کنیم

و تغییری در متغیر ایجاد کنید تی= گناه x(سپس dt= cos x dx ). سپس می گیریم

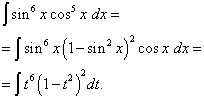
بیایید پرانتزها را باز کنیم

و دریافت می کنیم

با بازگشت به متغیر قدیمی، راه حل را دریافت می کنیم

مثال 6.پیدا کنید انتگرال یک تابع مثلثاتی

راه حل. نماهای سینوس و کسینوس زوج هستند. بنابراین تابع انتگرال را به صورت زیر تبدیل می کنیم:

سپس می گیریم

در انتگرال دوم تغییری در متغیر، تنظیم می کنیم تی= گناه2 x. سپس (1/2)dt= cos2 x dx . از این رو،

بالاخره می رسیم

با استفاده از روش جایگزینی متغیر

روش جایگزینی متغیرهنگام ادغام توابع مثلثاتی، می توان از آن در مواردی استفاده کرد که انتگرال فقط شامل سینوس یا فقط کسینوس، حاصل ضرب سینوس و کسینوس است که در آن سینوس یا کسینوس در درجه اول، مماس یا کوتانژانت و همچنین ضریب حتی قدرت های سینوس و کسینوس یک و همان استدلال. در این صورت، می توان نه تنها گناه را انجام داد x = تیو گناه x = تی، بلکه tg x = تیو ctg x = تی .

مثال 8.پیدا کنید انتگرال یک تابع مثلثاتی

.

راه حل. بیایید متغیر: , سپس را تغییر دهیم. انتگرال حاصل را می توان به راحتی با استفاده از جدول انتگرال ها ادغام کرد:

.

مثال 9.پیدا کنید انتگرال یک تابع مثلثاتی

راه حل. بیایید مماس را به نسبت سینوس و کسینوس تبدیل کنیم:

بیایید متغیر: , سپس را تغییر دهیم. انتگرال حاصل شده است انتگرال جدولبا علامت منفی:

.

با بازگشت به متغیر اصلی، در نهایت دریافت می کنیم:

.

مثال 10.پیدا کنید انتگرال یک تابع مثلثاتی

راه حل. بیایید متغیر: , سپس را تغییر دهیم.

بیایید انتگرال را برای اعمال هویت مثلثاتی تبدیل کنیم :

متغیر را تغییر می دهیم، فراموش نمی کنیم که یک علامت منفی جلوی انتگرال قرار دهیم (به بالا نگاه کنید، چه چیزی برابر است با dt). بعد، انتگرال را فاکتور می کنیم و با استفاده از جدول ادغام می کنیم:

با بازگشت به متغیر اصلی، در نهایت دریافت می کنیم:

.

انتگرال یک تابع مثلثاتی را خودتان پیدا کنید و سپس به حل آن نگاه کنید

جایگزینی مثلثاتی جهانی

جایگزینی مثلثاتی جهانی در مواردی که انتگرال تحت مواردی که در پاراگراف های قبلی مورد بحث قرار گرفت قرار نمی گیرد می توان از آن استفاده کرد. اصولاً وقتی سینوس یا کسینوس (یا هر دو) در مخرج کسری باشد. ثابت شده است که سینوس و کسینوس را می توان با عبارت دیگری حاوی مماس نصف زاویه اصلی به صورت زیر جایگزین کرد:

اما توجه داشته باشید که جایگزینی مثلثاتی جهانی اغلب مستلزم تبدیل‌های جبری کاملاً پیچیده است، بنابراین زمانی که هیچ روش دیگری جواب نمی‌دهد بهتر است از آن استفاده شود. اجازه دهید به مثال هایی نگاه کنیم که در آن، همراه با جایگزینی مثلثاتی جهانی، جایگزینی تحت علامت دیفرانسیل و روش ضرایب نامعین استفاده می شود.

مثال 12.پیدا کنید انتگرال یک تابع مثلثاتی

.

راه حل. راه حل. بهره ببریم جایگزینی مثلثاتی جهانی. سپس
.

کسرهای صورت و مخرج را در ضرب می کنیم و آن دو را بیرون می آوریم و جلوی علامت انتگرال قرار می دهیم. سپس

برای ادغام توابع گویا به شکل R(sin x، cos x)، از یک جایگزین استفاده می شود که به آن جانشینی مثلثاتی جهانی می گویند. سپس . جایگزینی مثلثاتی جهانی اغلب منجر به محاسبات بزرگ می شود. بنابراین، در صورت امکان، از جایگزین های زیر استفاده کنید.

ادغام توابع به طور منطقی به توابع مثلثاتی وابسته است

1. انتگرالهای شکل ∫ sin n xdx، ∫ cos n xdx، n> 0
الف) اگر n فرد باشد، باید یک توان sinx (یا cosx) را زیر علامت دیفرانسیل وارد کرد و از توان زوج باقیمانده باید به تابع مقابل منتقل شود.
ب) اگر n زوج باشد، از فرمول هایی برای کاهش درجه استفاده می کنیم
2. انتگرالهای شکل ∫ tg n xdx، ∫ ctg n xdx، که در آن n یک عدد صحیح است.
باید از فرمول ها استفاده کرد

3. انتگرال های شکل ∫ sin n x cos m x dx
الف) فرض کنید m و n دارای برابری های مختلف باشند. اگر n فرد باشد از جایگزینی t=sin x یا اگر m فرد باشد t=cos x استفاده می کنیم.
ب) اگر m و n زوج باشند، از فرمول هایی برای کاهش درجه استفاده می کنیم
2sin 2 x=1-cos2x، 2cos 2 x=1+cos2x.
4. انتگرال های فرم
اگر اعداد m و n همسان باشند، از جایگزینی t=tg x استفاده می کنیم. اغلب استفاده از تکنیک واحد مثلثاتی راحت است.
5. 🔻 sin(nx) cos(mx)dx، ∫ cos(mx) cos(nx)dx، 🔻 sin(mx) sin(nx)dx

بیایید از فرمول های تبدیل حاصل ضرب توابع مثلثاتی به مجموع آنها استفاده کنیم:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

نمونه ها
1. انتگرال ∫ cos 4 x·sin 3 xdx را محاسبه کنید.
جایگزین cos(x)=t را می سازیم. سپس ∫ cos 4 x sin 3 xdx =
2. انتگرال را محاسبه کنید.
با ساخت جایگزین sin x=t، دریافت می کنیم

3. انتگرال را پیدا کنید.
جایگزین tg(x)=t را می سازیم. جایگزینی، دریافت می کنیم

ادغام عبارات فرم R(sinx، cosx)

مثال شماره 1. محاسبه انتگرال ها:

راه حل.
الف) ادغام عبارات به شکل R(sinx، cosx)، که در آن R یک تابع گویا از sin x و cos x است، با استفاده از جایگزینی مثلثاتی جهانی tg(x/2) = t به انتگرال توابع گویا تبدیل می شوند.
سپس ما داریم

یک جانشینی مثلثاتی جهانی این امکان را فراهم می کند که از یک انتگرال به شکل ∫ R(sinx، cosx) dx به یک انتگرال یک تابع منطقی کسری برویم، اما اغلب چنین جایگزینی منجر به عبارات دست و پا گیر می شود. تحت شرایط خاص، جایگزین های ساده تر موثر هستند:

• اگر برابری R(-sin x، cos x) = -R(sin x، cos x)dx برآورده شود، جایگزینی cos x = t اعمال می شود.
• اگر برابری R(sin x, -cos x) = -R(sin x, cos x)dx برقرار باشد، آنگاه جایگزینی sin x = t.
• اگر برابری R(-sin x, -cos x) = R(sin x, cos x)dx برقرار باشد، آنگاه جایگزینی tgx = t یا ctg x = t.

در این مورد، برای یافتن انتگرال
اجازه دهید جایگزینی مثلثاتی جهانی tg(x/2) = t را اعمال کنیم.
سپس پاسخ دهید:

فرمول های مثلثاتی پایه و جایگزین های اساسی ارائه شده است. روش های ادغام توابع مثلثاتی بیان شده است - ادغام توابع گویا، حاصلضرب توابع توان sin x و cos x، حاصل ضرب چند جمله ای، نمایی و سینوس یا کسینوس، ادغام توابع مثلثاتی معکوس. روش های غیر استاندارد تحت تأثیر قرار می گیرند.

محتوا

روش های استاندارد برای ادغام توابع مثلثاتی

رویکرد کلی

ابتدا، در صورت لزوم، انتگرال باید طوری تبدیل شود که توابع مثلثاتی به یک آرگومان منفرد، که همان متغیر انتگرال است، بستگی داشته باشند.

برای مثال، اگر انتگرال بستگی به گناه (x+a)و cos(x+b)، سپس باید تبدیل را انجام دهید:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + گناه (x+a) گناه (b-a).
سپس جایگزین z = x+a را بسازید.

هنگامی که توابع مثلثاتی به یک آرگومان منطبق با متغیر انتگرال گیری بستگی دارند (مثلاً z است)، یعنی انتگرال فقط از توابعی مانند sin z, cos z, tg z, ctg z، سپس باید یک جایگزین انجام دهید
.
چنین جایگزینی منجر به ادغام توابع منطقی یا غیرمنطقی (در صورت وجود ریشه) می شود و به فرد اجازه می دهد تا انتگرال را در صورت ادغام در توابع ابتدایی محاسبه کند.

با این حال، اغلب می‌توانید روش‌های دیگری را پیدا کنید که به شما امکان می‌دهد انتگرال را به روشی کوتاه‌تر، بر اساس ویژگی‌های انتگرال، ارزیابی کنید. در زیر خلاصه ای از اصلی ترین روش ها آورده شده است.

روش‌های ادغام توابع منطقی sin x و cos x

توابع گویا از گناه xو cos xتوابعی هستند که از گناه x, cos xو هر ثابتی که از عملیات جمع، تفریق، ضرب، تقسیم و افزایش به یک توان صحیح استفاده می کند. آنها به شرح زیر تعیین می شوند: R (sin x, cos x).
این ممکن است شامل مماس ها و کوتانژانت ها نیز باشد، زیرا آنها از تقسیم سینوس بر کسینوس و بالعکس تشکیل می شوند.
.

انتگرال توابع گویا به شکل زیر است:
روشهای ادغام توابع مثلثاتی گویا به شرح زیر است.
1) جایگزینی همیشه به انتگرال یک کسر گویا می انجامد. با این حال، در برخی موارد، جایگزین هایی (این موارد در زیر ارائه شده است) وجود دارد که منجر به محاسبات کوتاه تری می شود. (sin x, cos x) 2) اگر R گناه x.
cos x → - cos x (sin x, cos x) 3) اگر R ضرب در -1 هنگام جایگزینیگناه x → - گناه x cos x.
، سپس جایگزینی t = (sin x, cos x) 4) اگر R 2) اگر Rمانند تعویض همزمان تغییر نمی کند ضرب در -1 هنگام جایگزینی، و ، سپس جایگزینی t = tg x یا t =.

ctg x
, , .

مثال ها:

حاصل ضرب توابع توان cos x و sin x

انتگرال های فرم

انتگرال توابع مثلثاتی گویا هستند. بنابراین، روش های ذکر شده در بخش قبل را می توان برای آنها اعمال کرد. روش‌های مبتنی بر ویژگی‌های این انتگرال‌ها در زیر مورد بحث قرار می‌گیرند. گناه x tg x cos xاگر m و n اعداد گویا باشند، یکی از جانشینی ها t =

انتگرال به انتگرال دوجمله ای دیفرانسیل کاهش می یابد.

;
;
;
.

اگر m و n اعداد صحیح باشند، ادغام با استفاده از فرمول های کاهش انجام می شود:
.

مثال:

انتگرال حاصل ضرب چند جمله ای و سینوس یا کسینوس
, ,
انتگرال های فرم:

;
.

ctg x
, .

که در آن P(x) یک چند جمله ای در x است، توسط قطعات یکپارچه می شوند. این فرمول های زیر را تولید می کند:

انتگرال حاصل ضرب چند جمله ای و سینوس یا کسینوس
, ,
انتگرال حاصل ضرب چند جمله ای، نمایی و سینوس یا کسینوس
که در آن P(x) یک چند جمله ای در x است که با استفاده از فرمول اویلر ادغام شده است e iax =تبر cos + تبر isin 1 ).
(جایی که من 2 = -
.
با جداسازی قسمت های واقعی و خیالی از نتیجه، انتگرال های اصلی به دست می آیند.

اگر m و n اعداد صحیح باشند، ادغام با استفاده از فرمول های کاهش انجام می شود:
.

روش های غیر استاندارد برای یکپارچه سازی توابع مثلثاتی

در زیر تعدادی از روش های غیر استاندارد وجود دارد که به شما امکان می دهد ادغام توابع مثلثاتی را انجام دهید یا ساده کنید.

وابستگی به (a sin x + b cos x)

اگر انتگرال فقط به a بستگی دارد sin x + b cos x، سپس استفاده از فرمول مفید است:
,
کجا .

به عنوان مثال

تفکیک کسرها از سینوس و کسینوس به کسرهای ساده تر

انتگرال را در نظر بگیرید
.
ساده ترین روش ادغام، تجزیه کسر به کسرهای ساده تر با استفاده از تبدیل است:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

ادغام کسرهای درجه اول

هنگام محاسبه انتگرال
,
جدا کردن قسمت صحیح کسر و مشتق مخرج راحت است
الف 1 گناه x + b 1 cos x =الف (a sin x + b cos x) +ب (a sin x + b cos x)" .
ثابت های A و B با مقایسه سمت چپ و راست به دست می آیند.

ادبیات مورد استفاده:
N.M. گانتر، R.O. کوزمین، مجموعه مسائل در ریاضیات عالی، "لان"، 2003.

همچنین ببینید:

انتگرال توابع مثلثاتی
نمونه هایی از راه حل ها

در این درس به انتگرال های توابع مثلثاتی می پردازیم، یعنی پر شدن انتگرال ها سینوس ها، کسینوس ها، مماس ها و کوتانژانت ها در ترکیب های مختلف خواهد بود. همه نمونه ها با جزئیات، قابل دسترس و قابل درک حتی برای یک قوری تجزیه و تحلیل خواهند شد.

برای مطالعه موفقیت‌آمیز انتگرال‌های توابع مثلثاتی، باید درک خوبی از ساده‌ترین انتگرال‌ها داشته باشید و همچنین بر برخی تکنیک‌های ادغام تسلط داشته باشید. می توانید در سخنرانی ها با این مطالب آشنا شوید انتگرال نامعین. نمونه هایی از راه حل هاو .

و اکنون ما نیاز داریم: جدول انتگرال ها, جدول مشتقاتو فهرست فرمول های مثلثاتی. تمامی وسایل کمک آموزشی در صفحه موجود است فرمول ها و جداول ریاضی. من توصیه می کنم همه چیز را چاپ کنید. من به ویژه روی فرمول های مثلثاتی تمرکز می کنم، آنها باید جلوی چشمان شما باشند- بدون این، راندمان کار به طور قابل توجهی کاهش می یابد.

اما ابتدا در مورد اینکه انتگرال ها در این مقاله چه هستند خیر. هیچ انتگرالی از فرم وجود ندارد، کسینوس، سینوس، ضرب در چند جمله ای (کمتر چیزی با مماس یا کوتانژانت). این گونه انتگرال ها توسط قطعات ادغام می شوند و برای یادگیری روش به درس Integration by Parts مراجعه کنید. نمونه هایی از راه حل ها همچنین در اینجا هیچ انتگرالی با "قوس" وجود ندارد - قوس الکتریکی، کمان و غیره، آنها نیز اغلب توسط قطعات ادغام می شوند.

هنگام یافتن انتگرال توابع مثلثاتی، از تعدادی روش استفاده می شود:

(4) ما از فرمول جدولی استفاده می کنیم ، تنها تفاوت این است که به جای "X" یک عبارت پیچیده داریم.

مثال 2

مثال 3

انتگرال نامعین را پیدا کنید.

کلاسیک این ژانر برای کسانی که در رقابت غرق می شوند. همانطور که احتمالا متوجه شدید، در جدول انتگرال ها هیچ انتگرالی مماس و کوتانژانت وجود ندارد، اما، با این وجود، چنین انتگرال هایی را می توان یافت.

(1) از فرمول مثلثاتی استفاده می کنیم

(2) تابع را زیر علامت دیفرانسیل می آوریم.

(3) از انتگرال جدول استفاده می کنیم .

مثال 4

انتگرال نامعین را پیدا کنید.

این یک مثال برای یک راه حل مستقل است، راه حل کامل و پاسخ در پایان درس است.

مثال 5

انتگرال نامعین را پیدا کنید.

درجه ما به تدریج افزایش می یابد =).
اول راه حل:

(1) ما از فرمول استفاده می کنیم

(2) از هویت مثلثاتی اصلی استفاده می کنیم ، که از آن نتیجه می شود که .

(3) صورت را بر مخرج جمله بر جمله تقسیم کنید.

(4) از ویژگی خطی بودن انتگرال نامعین استفاده می کنیم.

(5) با استفاده از جدول ادغام می کنیم.

مثال 6

انتگرال نامعین را پیدا کنید.

این یک مثال برای یک راه حل مستقل است، راه حل کامل و پاسخ در پایان درس است.

همچنین انتگرال هایی از مماس ها و کوتانژانت ها وجود دارد که در توان های بالاتر هستند. انتگرال مکعب مماس در درس مورد بحث قرار می گیرد چگونه مساحت یک شکل صاف را محاسبه کنیم؟انتگرال مماس (کتانژانت) به توان چهارم و پنجم را می توانید در صفحه بدست آورید. انتگرال های مختلط.

کاهش درجه انتگرال

این تکنیک زمانی کار می کند که توابع انتگرال با سینوس و کسینوس در داخل پر شده باشند حتیدرجه برای کاهش درجه از فرمول های مثلثاتی استفاده کنید , و، و آخرین فرمول اغلب در جهت مخالف استفاده می شود: .

مثال 7

انتگرال نامعین را پیدا کنید.

راه حل:

در اصل، اینجا چیز جدیدی وجود ندارد، به جز اینکه ما فرمول را اعمال کردیم (کاهش درجه انتگرال). لطفا توجه داشته باشید که من راه حل را کوتاه کرده ام. همانطور که تجربه کسب می کنید، انتگرال از را می توان به صورت شفاهی یافت، این باعث صرفه جویی در زمان می شود و در هنگام اتمام تکالیف کاملا قابل قبول است. در این مورد، توصیه می شود که قاعده را توصیف نکنید ، ابتدا انتگرال 1 را به صورت شفاهی می گیریم سپس از .

مثال 8

انتگرال نامعین را پیدا کنید.

این یک مثال برای یک راه حل مستقل است، راه حل کامل و پاسخ در پایان درس است.

این افزایش درجه وعده داده شده است:

مثال 9

انتگرال نامعین را پیدا کنید.

ابتدا راه حل، سپس نظرات:

(1) انتگرال را برای اعمال فرمول آماده کنید .

(2) ما در واقع فرمول را اعمال می کنیم.

(3) مخرج را مربع می کنیم و ثابت را از علامت انتگرال خارج می کنیم. می شد کمی متفاوت انجام داد، اما، به نظر من، راحت تر بود.

(4) ما از فرمول استفاده می کنیم

(5) در ترم سوم دوباره درجه را کاهش می دهیم، اما با استفاده از فرمول .

(6) ما اصطلاحات مشابهی را ارائه می کنیم (در اینجا من ترم به اصطلاح را تقسیم کردم و اضافه را انجام داد).

(7) در واقع، ما انتگرال، قانون خطی را می گیریم و روش قرار دادن تابع زیر علامت دیفرانسیل به صورت شفاهی انجام می شود.

(8) شانه زدن پاسخ.

! در یک انتگرال نامعین، پاسخ را اغلب می توان به روش های مختلفی نوشت

در مثالی که به تازگی در نظر گرفته شد، پاسخ نهایی می توانست متفاوت نوشته شود - باز کردن پرانتزها و حتی انجام این کار قبل از ادغام عبارت، یعنی پایان زیر برای مثال کاملاً قابل قبول است:

کاملاً ممکن است که این گزینه حتی راحت تر باشد ، من فقط آن را توضیح دادم همانطور که خودم به حل آن عادت دارم). در اینجا یک مثال معمولی دیگر برای یک راه حل مستقل وجود دارد:

مثال 10

انتگرال نامعین را پیدا کنید.

این مثال به دو صورت قابل حل است و ممکن است موفق شوید دو پاسخ کاملا متفاوت(به طور دقیق تر ، آنها کاملاً متفاوت به نظر می رسند ، اما از نظر ریاضی معادل خواهند بود). به احتمال زیاد منطقی ترین روش را نخواهید دید و با باز کردن براکت ها و استفاده از فرمول های مثلثاتی دیگر دچار مشکل خواهید شد. موثرترین راه حل در پایان درس آورده شده است.

برای خلاصه کردن پاراگراف، نتیجه می گیریم: هر انتگرال فرم ، کجا و - حتیاعداد، با روش کاهش درجه انتگرال حل می شود.
در عمل به انتگرال هایی با 8 و 10 درجه برخورد کردم و مجبور شدم با چند بار پایین آوردن درجه، آشفتگی وحشتناک آنها را حل کنم که نتیجه آن پاسخ های طولانی و طولانی بود.

روش جایگزینی متغیر

همانطور که در مقاله ذکر شد روش تغییر متغیر در انتگرال نامعین، پیش نیاز اصلی برای استفاده از روش جایگزینی این واقعیت است که در انتگرال یک تابع مشخص و مشتق آن وجود دارد:
(کارکردها لزوماً در محصول نیستند)

مثال 11

انتگرال نامعین را پیدا کنید.

ما به جدول مشتقات نگاه می کنیم و به فرمول ها توجه می کنیم، ، یعنی در انتگرال ما یک تابع و مشتق آن وجود دارد. اما می بینیم که در حین تمایز، کسینوس و سینوس متقابلاً به یکدیگر تبدیل می شوند و این سؤال پیش می آید که چگونه تغییر متغیر را انجام دهیم و منظور از سینوس یا کسینوس چیست؟! این سوال را می توان با پوک زدن علمی حل کرد: اگر جایگزینی را اشتباه انجام دهیم، هیچ چیز خوبی از آن حاصل نمی شود.

یک دستورالعمل کلی: در موارد مشابه، باید تابعی را که در مخرج است مشخص کنید.

محلول را قطع می کنیم و جایگزین می کنیم

همه چیز در مخرج خوب است، همه چیز فقط به بستگی دارد، اکنون باید دریابیم که به چه چیزی تبدیل خواهد شد.
برای انجام این کار، دیفرانسیل را پیدا می کنیم:

یا به طور خلاصه:
از برابری حاصل، با استفاده از قاعده تناسب، عبارت مورد نیاز خود را بیان می کنیم:

بنابراین:

اکنون کل یکپارچگی ما فقط به این بستگی دارد و می توانیم به حل ادامه دهیم

آماده است. اجازه دهید به شما یادآوری کنم که هدف از جایگزینی ساده کردن انتگرال است، در این مورد همه چیز به ادغام تابع قدرت مطابق جدول خلاصه شد.

تصادفی نیست که این مثال را با این جزئیات شرح دادم، این کار به منظور تکرار و تقویت مطالب درسی انجام شد روش تغییر متغیر در انتگرال نامعین.

و حالا دو مثال برای راه حل خودتان:

مثال 12

انتگرال نامعین را پیدا کنید.

مثال 13

انتگرال نامعین را پیدا کنید.

راه حل ها و پاسخ ها را در پایان درس کامل کنید.

مثال 14

انتگرال نامعین را پیدا کنید.

در اینجا، در انتگرال، سینوس و کسینوس (یک تابع با مشتق) وجود دارد، اما در یک محصول، و یک دوراهی پیش می‌آید - منظور ما از سینوس یا کسینوس چیست؟

می توانید با استفاده از پوک علمی جایگزینی را انجام دهید، و اگر هیچ چیز جواب نداد، آن را به عنوان عملکرد دیگری تعیین کنید، اما وجود دارد:

دستورالعمل کلی: شما باید عملکردی را مشخص کنید که به طور مجازی در "موقعیت ناراحت کننده" است..

می بینیم که در این مثال، کسینوس دانش آموز از درجه «مصائب» می شود، و سینوس آزادانه، به تنهایی می نشیند.

بنابراین، بیایید یک جایگزین ایجاد کنیم:

اگر کسی هنوز با الگوریتم جایگزینی یک متغیر و یافتن دیفرانسیل مشکل دارد، باید به درس برگردید. روش تغییر متغیر در انتگرال نامعین.

مثال 15

انتگرال نامعین را پیدا کنید.

بیایید انتگرال را تجزیه و تحلیل کنیم، با چه چیزی باید نشان داده شود؟
بیایید دستورالعمل های خود را به خاطر بسپاریم:
1) تابع به احتمال زیاد در مخرج است.
2) عملکرد در "موقعیت نامناسب" قرار دارد.

به هر حال، این دستورالعمل ها نه تنها برای توابع مثلثاتی معتبر هستند.

سینوس با هر دو معیار مطابقت دارد (مخصوصاً دوم)، بنابراین جایگزینی خود را پیشنهاد می کند. در اصل ، جایگزینی قبلاً قابل انجام است ، اما ابتدا خوب است که بفهمیم با چه کاری باید انجام دهیم؟ ابتدا، یک کسینوس را "نیز" می کنیم:

ما برای دیفرانسیل "آینده" خود رزرو می کنیم

و ما آن را از طریق سینوس با استفاده از هویت مثلثاتی اصلی بیان می کنیم:

حالا این جایگزین است:

قانون کلی: اگر در انتگرال یکی از توابع مثلثاتی (سینوس یا کسینوس) در عجیب و غریبدرجه، سپس باید یک تابع را از درجه فرد «گزیده» کنید و تابع دیگری را پشت آن تعیین کنید.ما فقط در مورد انتگرال صحبت می کنیم که کسینوس و سینوس وجود دارد.

در مثال مورد بررسی، ما یک کسینوس با توان فرد داشتیم، بنابراین یک کسینوس را از توان جدا کردیم و آن را به عنوان سینوس تعیین کردیم.

مثال 16

انتگرال نامعین را پیدا کنید.

درجه در حال افزایش است =).
این یک مثال برای شماست که خودتان آن را حل کنید. حل کامل و پاسخ در پایان درس.

جایگزینی مثلثاتی جهانی

جایگزینی مثلثاتی جهانی یک مورد رایج از روش جایگزینی متغیر است. می‌توانید زمانی که «نمی‌دانید چه کار کنید» از آن استفاده کنید. اما در واقع دستورالعمل هایی برای کاربرد آن وجود دارد. انتگرال های معمولی که در آن جانشینی مثلثاتی جهانی باید اعمال شود انتگرال های زیر هستند: , , , و غیره

مثال 17

انتگرال نامعین را پیدا کنید.

جایگزینی مثلثاتی جهانی در این مورد به روش زیر اجرا می شود. بیایید جایگزین کنیم: . من از حرف استفاده نمی‌کنم، اما از حرف، این نوعی قانون نیست، فقط این است که، دوباره، من عادت دارم مسائل را به این شکل حل کنم.

در اینجا پیدا کردن تفاوت برای این کار راحت تر است، من بیان می کنم:
من یک آرکتانژانت را به هر دو قسمت وصل می کنم:

تانژانت و مماس یکدیگر را خنثی می کنند:

بدین ترتیب:

در عمل، لازم نیست آن را با جزئیات توصیف کنید، بلکه به سادگی از نتیجه نهایی استفاده کنید:

! این عبارت فقط در صورتی معتبر است که در زیر سینوس ها و کسینوس ها به سادگی "X" برای انتگرال داشته باشیم (که بعداً در مورد آن صحبت خواهیم کرد) همه چیز کمی متفاوت خواهد بود!

هنگام جایگزینی، سینوس ها و کسینوس ها به کسرهای زیر تبدیل می شوند:
، این برابری ها بر اساس فرمول های مثلثاتی شناخته شده هستند: ,

بنابراین، طراحی نهایی می تواند شبیه به این باشد:

بیایید یک جایگزین مثلثاتی جهانی انجام دهیم: