Vektori pikkuse omadused eukleidilises ruumis. Eukleidilised ruumid
Eukleidiline ruum
Eukleidiline ruum(Samuti Eukleidiline ruum) – algses tähenduses ruum, mille omadusi kirjeldavad eukleidilise geomeetria aksioomid. Sel juhul eeldatakse, et ruumi mõõde on 3.
Tänapäeva mõistes, üldisemas mõttes, võib see tähistada üht allpool määratletud sarnastest ja tihedalt seotud objektidest. Tavaliselt tähistatakse -dimensioonilist eukleidilist ruumi tähisega , kuigi sageli kasutatakse mitte täiesti vastuvõetavat tähistust.
,kõige lihtsamal juhul ( Eukleidese norm):
kus (eukleidilises ruumis saate alati valida aluse, milles see lihtsaim versioon on tõsi).
2. Meetriline ruum, mis vastab ülalkirjeldatud ruumile. See tähendab, et mõõdik on sisestatud vastavalt valemile:
,Seotud määratlused
- Under Eukleidese meetrika võib mõista nii ülalkirjeldatud mõõdikuna kui ka vastava Riemanni mõõdikuna.
- Lokaalse eukleidilisuse all peame tavaliselt silmas seda, et iga Riemanni kollektori puutujaruum on eukleidiline ruum koos kõigi sellest tulenevate omadustega, näiteks võimalusega (meetria sujuvuse tõttu) sisestada koordinaate punkti väikeses naabruses, kus kaugust väljendatakse (mingi suurusjärguni) ) nagu eespool kirjeldatud.
- Meetrilist ruumi nimetatakse ka lokaalselt eukleidiliseks, kui sellele on võimalik igal pool (või vähemalt lõplikul domeenil) sisestada koordinaadid, milles mõõdik on eukleidiline (teise definitsiooni tähenduses) - mis näiteks on nullkõverusega Riemanni kollektor.
Näited
Eukleidiliste ruumide illustreerivad näited on järgmised ruumid:
Abstraktsem näide:
Variatsioonid ja üldistused
Vaata ka
Lingid
Wikimedia sihtasutus.
2010. aasta.
Vaadake, mis on "eukleidiline ruum" teistes sõnaraamatutes: Lõpliku mõõtmega vektorruum positiivse kindla skalaarkorrutisega. On otsene. tavalise kolmemõõtmelise ruumi üldistamine. E. ruumis on ristkoordinaadid, milles (xy)vektorite skalaarkorrutis x...
Ruum, mille omadusi uuritakse eukleidilises geomeetrias. Laiemas mõttes on eukleidiline ruum n-mõõtmeline vektorruum, milles skalaarkorrutis ... Suur entsüklopeediline sõnaraamat
Eukleidiline ruum- ruum, mille omadusi kirjeldavad Eukleidilise geomeetria aksioomid. Lihtsustatult võib eukleidilist ruumi määratleda kui ruumi tasapinnal või kolmemõõtmelises ruumalas, milles on antud ristkülikukujulised (Cartesiuse) koordinaadid ja... ... Kaasaegse loodusteaduse algus
Eukleidiline ruum- vt Mitmemõõtmeline (n-mõõtmeline) vektorruum, Vektori (lineaarne) ruum... Majandus- ja matemaatikasõnastik
Eukleidiline ruum- - [L.G. Sumenko. Inglise-vene infotehnoloogia sõnaraamat. M.: Riigiettevõte TsNIIS, 2003.] Teemad infotehnoloogiaüldiselt EN Descartes'i ruum... Tehniline tõlkija juhend
Ruum, mille omadusi uuritakse eukleidilises geomeetrias. Laiemas mõttes on eukleidiline ruum n-mõõtmeline vektorruum, milles skalaarkorrutis on defineeritud. * * * EUCLIDEAN RUUM EUCLIDEAN... ... Entsüklopeediline sõnaraamat
Ruum, mille omadusi uuritakse eukleidilises geomeetrias. Laiemas mõttes nimetatakse E. p. n-mõõtmeline vektorruum, milles skalaarkorrutis ... Loodusteadus. Entsüklopeediline sõnaraamat
Ruum, mille omadusi kirjeldavad Eukleidilise geomeetria aksioomid. Üldisemas mõttes on E. ruum lõpliku mõõtmega reaalvektori ruum Rn, mille skalaarkorrutis (x, y), x, sobivalt valitud koordinaatides... ... Matemaatiline entsüklopeedia
- (matemaatikas) ruum, mille omadusi kirjeldavad Eukleidilise geomeetria aksioomid (vt Eukleidiline geomeetria). Üldisemas mõttes nimetatakse E. ruumi n-mõõtmeliseks Vektorruumiks, milles on võimalik tutvustada mõnda erilist... ... Suur Nõukogude entsüklopeedia
- [nimetatud teise kreeklase järgi. Eukleidese matemaatika (Eukleides; 3. saj eKr)] ruum, sealhulgas mitmemõõtmeline, millesse on võimalik sisestada koordinaadid x1,..., xn nii, et punktide M (x1 ..., kaugus p (M, M), x n) ja M (x 1, .... xn) võib-olla... ... Suur entsüklopeediline polütehniline sõnaraamat
§3. Vektorruumi mõõde ja alus
Lineaarne vektorite kombinatsioon
Triviaalne ja mittetriviaalne lineaarne kombinatsioon
Lineaarselt sõltuvad ja lineaarselt sõltumatud vektorid
Vektorite lineaarse sõltuvusega seotud vektorruumi omadused
n-mõõtmeline vektorruum
Vektorruumi mõõde
Vektori dekomponeerimine baasiks
§4. Üleminek uuele alusele
Üleminekumaatriks vanalt aluselt uuele
Vektorkoordinaadid uues baasis
§5. Eukleidiline ruum
Dot toode
Eukleidiline ruum
Vektori pikkus (norm).
Vektori pikkuse omadused
Nurk vektorite vahel
Ortogonaalsed vektorid
Ortonormaalne alus
§ 3. Vektorruumi mõõde ja alus
Vaatleme mingit vektorruumi (V, Å, ∘) välja kohal R. Olgu mõned hulga V elemendid, s.o. vektorid.
Lineaarne kombinatsioon vektorid on mis tahes vektor, mis on võrdne nende vektorite korrutistega välja suvaliste elementide kaupa R(st skalaaridel):
Kui kõik skalaarid on võrdsed nulliga, siis nimetatakse sellist lineaarset kombinatsiooni triviaalne(kõige lihtsam) ja .
Kui vähemalt üks skalaar on nullist erinev, kutsutakse lineaarne kombinatsioon mittetriviaalne.
Vektoreid nimetatakse lineaarselt sõltumatu, kui ainult nende vektorite triviaalne lineaarne kombinatsioon on võrdne:
Vektoreid nimetatakse lineaarselt sõltuv, kui nende vektorite mittetriviaalne lineaarne kombinatsioon on võrdne .
Näide. Mõelge järjestatud neljakordsete komplektide komplektile reaalarvud on vektorruum reaalarvude välja kohal. Ülesanne: uuri, kas vektorid on ![]() ,
, ![]() Ja
Ja ![]() lineaarselt sõltuv.
lineaarselt sõltuv.
Lahendus.
Teeme nendest vektoritest lineaarse kombinatsiooni: , kus on tundmatud arvud. Nõuame, et see lineaarne kombinatsioon oleks võrdne nullvektoriga: .
Selles võrdsuses kirjutame vektorid arvude veergudena:

Kui on numbreid, mille puhul see võrdus kehtib, ja vähemalt üks arvudest ei ole võrdne nulliga, siis on tegemist mittetriviaalse lineaarse kombinatsiooniga ja vektorid on lineaarselt sõltuvad.
Teeme järgmist.


Seega taandub probleem süsteemi lahendamisele lineaarvõrrandid:

Selle lahendades saame:

Süsteemi laiendatud ja põhimaatriksite järgud on võrdsed ja tundmatute arvust väiksemad, seetõttu on süsteemil lõpmatu arv lahendeid.
Laske siis ja .
Seega on nende vektorite jaoks olemas mittetriviaalne lineaarne kombinatsioon, näiteks juures , mis on võrdne nullvektoriga, mis tähendab, et need vektorid on lineaarselt sõltuvad.
Märgime mõned vektorruumi omadused, mis on seotud vektorite lineaarse sõltuvusega:
1. Kui vektorid on lineaarselt sõltuvad, siis vähemalt üks neist on teiste lineaarne kombinatsioon.
2. Kui vektorite hulgas on nullvektor, siis on need vektorid lineaarselt sõltuvad.
3. Kui mõned vektoritest on lineaarselt sõltuvad, siis kõik need vektorid on lineaarselt sõltuvad.
Vektorruumi V nimetatakse n-mõõtmeline vektorruum, kui see sisaldab n lineaarselt sõltumatud vektorid ja mis tahes hulk ( n+ 1) vektorid on lineaarselt sõltuvad.
Number n helistas vektorruumi mõõde, ja on tähistatud hämar (V) inglise keelest "dimension" - mõõde (mõõt, suurus, mõõde, suurus, pikkus jne).
Totaalsus n lineaarselt sõltumatud vektorid n-nimetatakse mõõtmelist vektorruumi alusel.
|
Valemit (*) nimetatakse vektori lagunemine alusel ja numbrid – vektori koordinaadid sellel alusel .
Vektorruumil võib olla rohkem kui üks või isegi lõpmatult palju aluseid. Igas uues baasis on samal vektoril erinevad koordinaadid.
§ 4. Üleminek uuele alusele
Lineaaralgebras tekib sageli probleem vektori koordinaatide leidmisega uues baasis, kui on teada selle koordinaadid vanas baasis.
Vaatame mõnda n-mõõtmeline vektorruum (V, +, ·) üle välja R. Olgu selles ruumis kaks alust: vana ja uus ![]() .
.
Ülesanne: leida uues baasis vektori koordinaadid.
Olgu vana baasi uue aluse vektoritel laiendus:
 ,
,
Kirjutame vektorite koordinaadid maatriksisse mitte ridadena, nagu süsteemis kirjas, vaid veergudes:

Saadud maatriksit nimetatakse üleminekumaatriks vanast alusest uuele.
Üleminekumaatriks ühendab mis tahes vektori koordinaadid vanal ja uuel alusel järgmise seosega:
 ,
,
kus on vektori soovitud koordinaadid uues baasis.
Seega taandub vektori koordinaatide leidmise ülesanne uues baasis maatriksvõrrandi lahendamiseks: , kus X- vektori koordinaatide maatriks-veerg vanal alusel, A- üleminekumaatriks vanalt aluselt uuele, X* – uues baasis vajalik vektori koordinaatide maatriks-veerg. Maatriksvõrrandist saame:
Niisiis, vektori koordinaadid uuel alusel on leitud võrdsusest:
 .
.
Näide. Teatud alusel antakse vektorite jaotused:
Leia baasist vektori koordinaadid.
Lahendus.
1. Kirjutame välja üleminekumaatriksi uuele alusele, s.t. Kirjutame vana aluse vektorite koordinaadid veergudesse:

2. Leidke maatriks A –1:


3. Tehke korrutamine , kus on vektori koordinaadid:
Vastus: ![]() .
.
§ 5. Eukleidiline ruum
Vaatame mõnda n-mõõtmeline vektorruum (V, +, ·) reaalarvude välja kohal R. Olgu selle ruumi alus.
Tutvustame selles vektorruumis meetriline, st. Määrame meetodi pikkuste ja nurkade mõõtmiseks. Selleks defineerime skalaarkorrutise mõiste.
Isegi koolis tutvustatakse kõigile õpilastele kontseptsiooni "eukleidiline geomeetria", mille põhisätted on keskendunud mitmele aksioomile, mis põhinevad sellistel geomeetrilistel elementidel nagu punkt, tasapind, sirgjoon ja liikumine. Kõik need kokku moodustavad nn eukleidilise ruumi.
Eukleidiline, mis põhineb vektorite skalaarkorrutamise põhimõttel, on lineaarse (afiinse) ruumi erijuhtum, mis rahuldab mitmeid nõudeid. Esiteks on vektorite skalaarkorrutis absoluutselt sümmeetriline, st koordinaatidega (x;y) vektor on kvantitatiivselt identne koordinaatidega (y;x), kuid vastupidise suunaga vektoriga.
Teiseks, kui vektori skalaarkorrutis sooritatakse iseendaga, on selle toimingu tulemus positiivne. Ainus erand on juhtum, kui selle vektori alg- ja lõppkoordinaadid on võrdsed nulliga: sel juhul on selle korrutis iseendaga samuti võrdne nulliga.

Kolmandaks on skalaarkorrutis distributiivne, st võimalus lagundada üks selle koordinaatidest kahe väärtuse summaks, mis ei too kaasa muudatusi vektorite skalaarkorrutise lõpptulemuses. Lõpuks, neljandaks, vektorite korrutamisel sama asjaga suureneb ka nende skalaarkorrutis sama palju.
Kui kõik need neli tingimust on täidetud, võime kindlalt väita, et see on eukleidiline ruum.
Praktilisest vaatenurgast saab eukleidilist ruumi iseloomustada järgmiste konkreetsete näidetega:

- Lihtsaim juhtum on vektorite komplekti olemasolu skalaarkorrutisega, mis on defineeritud vastavalt geomeetria põhiseadustele.
- Eukleidiline ruum saadakse ka siis, kui vektorite abil mõistame teatud reaalarvude lõplikku kogumit, mille valem kirjeldab nende skalaarsummat või korrutist.
- Eukleidilise ruumi erijuhtumit tuleks tunnustada nn nullruumina, mis saadakse siis, kui mõlema vektori skalaarpikkus on võrdne nulliga.
Eukleidilisel ruumil on mitmeid spetsiifilisi omadusi. Esiteks saab skalaarkorrutise esimesest ja teisest tegurist sulgudest välja võtta skalaarteguri, tulemus ei muutu. Teiseks, koos skalaarkorrutise esimese elemendi distributiivsusega toimib ka teise elemendi jaotus. Lisaks ilmneb vektorite lahutamise korral lisaks vektorite skalaarsummale ka distributiivsus. Lõpuks, kolmandaks, vektori skalaarkorrutamisel nulliga on tulemus samuti võrdne nulliga.
Seega on eukleidiline ruum kõige olulisem geomeetriline mõiste, mida kasutatakse vektorite suhtelise asukohaga seotud ülesannete lahendamisel, mida iseloomustab skalaarkorrutise mõiste.
Eukleidilise ruumi definitsioon
Definitsioon 1. Tõeliseks lineaarruumiks nimetatakse eukleidiline, Kui see määratleb operatsiooni, mis seob mis tahes kaks vektorit x Ja y sellest ruumiarvu, mida nimetatakse vektorite skalaarkorrutiseks x Ja y ja määratud(x,y), mille puhul on täidetud järgmised tingimused:
1. (x,y) = (y,x);
2. (x + y,z) = (x,z) + (y,z) , kus z- mis tahes vektor, mis kuulub antud lineaarruumi;
3. (?x,y) = ? (x,y) , kus ? - mis tahes arv;
4. (x,x) ? 0 ja (x,x) = 0 x = 0.
Näiteks üheveeruliste maatriksite lineaarruumis vektorite skalaarkorrutis

saab määrata valemiga

Eukleidese dimensiooniruum n tähistavad Ent. Pange tähele, et On olemas nii lõpliku kui ka lõpmatu mõõtmega eukleidilised ruumid.
2. definitsioon. Vektori x pikkus (moodul). eukleidilises ruumis En helistas (x,x) ja tähistage seda järgmiselt: |x| = (x,x). Eukleidilise ruumi mis tahes vektori jaokson pikkus ja nullvektoril on see võrdne nulliga.
Nullist erineva vektori korrutamine x numbri kohta , saame vektori, pikkus mis on võrdne ühega. Seda operatsiooni nimetatakse normeerimine vektor x.
Näiteks üheveeruliste maatriksite ruumis vektori pikkus saab määrata järgmise valemiga: ![]()
Cauchy-Bunyakovsky ebavõrdsus
Kas lasta x? En ja y? En – suvalised kaks vektorit. Tõestame, et ebavõrdsus kehtib nende kohta:
![]() (Cauchy-Bunyakovsky ebavõrdsus)
(Cauchy-Bunyakovsky ebavõrdsus)
Tõestus. Lase? - mis tahes reaalarv. See on ilmne (?x? y,?x? y) ? 0. Seevastu skalaarkorrutise omaduste tõttu saame kirjutada
Sain aru
Selle ruuttrinoomi diskriminant ei saa olla positiivne, s.t. , millest järeldub:
Ebavõrdsus on tõestatud.
Kolmnurga ebavõrdsus
Lase x Ja y- eukleidilise ruumi En suvalised vektorid, s.o. x? En ja y? En.
Tõestame seda ![]() . (Kolmnurga ebavõrdsus).
. (Kolmnurga ebavõrdsus).
Tõestus.
See on ilmne ![]() Teisel pool,.
Võttes arvesse Cauchy-Bunyakovsky ebavõrdsust, saame
Teisel pool,.
Võttes arvesse Cauchy-Bunyakovsky ebavõrdsust, saame
Kolmnurga ebavõrdsus on tõestatud.
Eukleidilise ruumi norm
Definitsioon 1 . Lineaarne ruum?helistas meetriline, kui on selle ruumi kaks elementi x Ja y sobitatud mittenegatiivnenumber? (x,y), mida nimetatakse vahemaaks x Ja y , (? (x,y)? 0) ja need täidetaksetingimused (aksioomid):
1) ? (x,y) = 0 x = y
2) ? (x,y) = ? (y,x)(sümmeetria);
3) mis tahes kolme vektori jaoks x, y Ja z see ruum? (x,y) ? ? (x, z) + ? (z,y).
Kommenteeri. Meetrilise ruumi elemente nimetatakse tavaliselt punktideks.
Eukleidiline ruum En on meetriline ja vahemaa vektorid x? En ja y? En võib võtta x ? y.
Nii näiteks üheveeruliste maatriksite ruumis, kus

seega
2. definitsioon . Lineaarne ruum?helistas normaliseeritud, Kui iga vektor x sellest ruumist on seotud mittenegatiivsega number kutsus seda norm x. Sel juhul on aksioomid täidetud:
On lihtne mõista, et normruum on meetriline ruum stvom. Tegelikult nagu vahemaa x Ja y võib võtta. Eukleidese keelesruum En kui mis tahes vektori x norm? En on selle pikkus, need. .
Seega on eukleidiline ruum En meetriline ruum ja pealegi Eukleidiline ruum En on normruum.
Nurk vektorite vahel
Definitsioon 1
. Nurgast erineva vektorite vaheline nurk a Ja b Eukleidiline ruumkvaliteet E n nimetage number, mille jaoks 
2. definitsioon . Vektorid x Ja y Eukleidiline ruum En kutsutakse ortogonlinane, kui nende jaoks kehtib võrdsus (x,y) = 0.
Kui x Ja y- on nullist erinevad, siis definitsioonist järeldub, et nendevaheline nurk on võrdne
Pange tähele, et nullvektorit peetakse definitsiooni järgi iga vektori suhtes ortogonaalseks.
Näide . Geomeetrilises (koordinaat)ruumis?3, mis on eukleidilise ruumi erijuhtum, ühikvektorid i, j Ja k vastastikku ortogonaalsed.
Ortonormaalne alus
Definitsioon 1 . Alus e1,e2 ,...,en nimetatakse eukleidilist ruumi En ortogonlinane, kui selle aluse vektorid on paarikaupa ortogonaalsed, st. Kui
2. definitsioon . Kui kõik ortogonaalbaasi vektorid e1, e2 ,...,en on ühtsed, s.o. e i = 1 (i = 1,2,...,n) , siis kutsutakse alus ortonormaalne, st. Sestortonormaalne alus

Teoreem. (ortonormaalse konstruktsiooni alusel)
Igas Eukleidilises ruumis E n eksisteerivad ortonormaalsed alused.
Tõestus . Tõestame teoreemi juhtumi jaoks n = 3.
Olgu E1 ,E2 ,E3 mingi suvaline eukleidilise ruumi E3 alus Ehitame mingi ortonormaalse aluseselles ruumis.Paneme kuhu ? - mõni reaalarv, mille me valimenii et (e1 ,e2 ) = 0, siis saame
ja mis on ilmselge? = 0, kui E1 ja E2 on ortogonaalsed, st. sel juhul e2 = E2 ja , sest see on baasvektor.
Arvestades, et (e1 ,e2 ) = 0, saame 
On ilmne, et kui e1 ja e2 on vektori E3 suhtes ortogonaalsed, s.o. sel juhul peaksime võtma e3 = E3. Vektor E3? 0 sest E1, E2 ja E3 on lineaarselt sõltumatud,seega e3 ? 0.
Lisaks järeldub ülaltoodud arutluskäigust, et e3 ei saa vormis esitada vektorite e1 ja e2 lineaarne kombinatsioon, seetõttu on vektorid e1, e2, e3 lineaarselt sõltumatudsimsid ja on paarikaupa ortogonaalsed, seega võib neid võtta eukleidilise alusenatühik E3. Jääb vaid konstrueeritud alust normaliseerida, selleks piisabjagage kõik konstrueeritud vektorid selle pikkusega. Siis saame

Seega oleme loonud aluse - ortonormaalne alus. Teoreem on tõestatud.
Rakendatud meetod ortonormaalse aluse konstrueerimiseks meelevaldsest alust nimetatakse ortogonaliseerimisprotsess . Pange tähele, et tõendamise protsessisteoreemiga tuvastasime, et paarikaupa ortogonaalsed vektorid on lineaarselt sõltumatud. Välja arvatud kui on ortonormaalne alus keeles En, siis mis tahes vektori x jaoks? Enon ainult üks lagunemine
kus x1, x2,..., xn on vektori x koordinaadid selles ortonormaalses baasis.
Sest
 seejärel korrutades võrdsuse (*) skalaarselt, saame
seejärel korrutades võrdsuse (*) skalaarselt, saame ![]() .
.
Järgnevalt käsitleme ainult ortonormaalseid aluseid ja seega kirjutamise hõlbustamiseks on nullid baasvektorite kohaljätame vahele.
 Geoloogiline kronoloogia Paleontoloogiline meetod põhineb kivimikihtidesse mattunud fossiilsete organismide ja taimede uurimisel.
Geoloogiline kronoloogia Paleontoloogiline meetod põhineb kivimikihtidesse mattunud fossiilsete organismide ja taimede uurimisel. Müüdid loovusest, mis osutusid valeks, kuid siiski mürgitavad meie elu
Müüdid loovusest, mis osutusid valeks, kuid siiski mürgitavad meie elu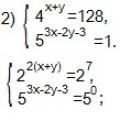 Eksponentvõrrandite ja võrratuste lahendamine
Eksponentvõrrandite ja võrratuste lahendamine