Integraalitüübid ja lahendusmeetodid. Integreerimine muutuja meetodi muutmisega
Kutsutakse välja antud intervallis X diferentseeruv funktsioon F(x). funktsiooni antiderivaat f(x) või f(x) integraal, kui iga x ∈X korral kehtib järgmine võrdsus:
F " (x) = f (x). (8.1)
Antud funktsiooni kõigi antiderivaatide leidmist nimetatakse selle funktsiooniks integratsiooni. Määramatu integraalfunktsioon f(x) antud intervallil X on funktsiooni f(x) kõigi antiderivatiivfunktsioonide hulk; nimetus -
Kui F(x) on funktsiooni f(x) antituletis, siis ∫ f(x)dx = F(x) + C, (8.2)
kus C on suvaline konstant.
Integraalide tabel
Otse definitsioonist saame peamised omadused Mitte kindel integraal ja tabeliintegraalide loend:
1) d∫f(x)dx=f(x)
2)∫df(x)=f(x)+C
3) ∫af(x)dx=a∫f(x)dx (a=const)
4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx
Tabeliintegraalide loend
1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)
3.∫a x dx = a x /ln a + C (a>0, a ≠1)
4.∫e x dx = e x + C
5.∫sin x dx = cosx + C
6.∫cos x dx = - sin x + C
7. = arctan x + C
8. = arcsin x + C
10. = - ctg x + C
Muutuv asendus
Paljude funktsioonide integreerimiseks kasutage muutuja asendusmeetodit või asendused, mis võimaldab integraalid taandada tabelikujuliseks.
Kui funktsioon f(z) on pidev [α,β], on funktsioonil z =g(x) pidev tuletis ja α ≤ g(x) ≤ β, siis
∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)
Peale selle tuleks pärast parempoolset integreerimist teha asendus z=g(x).
Selle tõestamiseks piisab, kui kirjutada algne integraal kujul:
∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).
Näiteks:
Osade kaupa integreerimise meetod
Olgu u = f(x) ja v = g(x) funktsioonid, millel on pidev . Siis vastavalt tööle
d(uv))= udv + vdu või udv = d(uv) - vdu.
Avaldise d(uv) puhul on antiderivatiiv ilmselgelt uv, seega kehtib valem:
∫ udv = uv - ∫ vdu (8.4.)
See valem väljendab reeglit integreerimine osade kaupa. See viib avaldise udv=uv"dx integreerimise avaldise vdu=vu"dx integreerimiseni.
Olgu näiteks, et soovite leida ∫xcosx dx. Paneme u = x, dv = cosxdx, seega du=dx, v=sinx. Siis
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Osade kaupa integreerimise reeglil on piiratum ulatus kui muutujate asendamisel. Kuid on terveid integraalide klasse, näiteks
∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax ja teised, mis arvutatakse täpselt, kasutades osade kaupa integreerimist.
Kindel integraal
Kindla integraali mõiste tutvustatakse järgmiselt. Olgu funktsioon f(x) määratletud intervallil. Jagame lõigu [a,b] n osad punktide kaupa a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 ,
x i) возьмем произвольную точку ξ i и составим сумму f(ξ i)
Δx i где
Δ x i =x i - x i-1. Nimetatakse summa kujul f(ξ i)Δ x i integraalsumma, ja selle piirväärtust λ = maxΔx i → 0, kui see on olemas ja on lõplik, nimetatakse kindel integraal funktsioonid f(x) of a juurde b ja on määratud:
F(ξ i)Δx i (8,5).
Sel juhul kutsutakse funktsioon f(x). integreeritav intervalliga, kutsutakse numbreid a ja b integraali alumine ja ülemine piir.
Järgmised omadused kehtivad kindla integraali kohta:
4), (k = const, k∈R);
5)![]()
6)![]()
7) f(ξ)(b-a) (ξ∈).
Viimane omadus on nn keskmise väärtuse teoreem.
Olgu f(x) pidev . Siis on sellel lõigul määramatu integraal
∫f(x)dx = F(x) + C
ja toimub Newtoni-Leibnizi valem, mis ühendab kindla integraali määramata integraaliga:
F(b) - F(a). (8,6)
Geomeetriline tõlgendus: kindel integraal on kõverjoonelise trapetsi pindala, mida ülalt piiravad kõver y=f(x), sirged x = a ja x = b ning telje segment Ox.
Valed integraalid
Lõpmatute piiridega integraale ja katkendlike (piiramata) funktsioonide integraale nimetatakse mitte sinu oma. Esimest tüüpi valed integraalid - Need on integraalid lõpmatu intervalliga, mis on määratletud järgmiselt:
![]() (8.7)
(8.7)
Kui see piir on olemas ja on lõplik, siis seda nimetatakse f(x) koonduv vale integraal intervallil [a,+ ∞) ja kutsutakse funktsioon f(x). integreeritav lõpmatu intervalliga[a,+ ∞). Vastasel juhul öeldakse, et integraal on ei eksisteeri või lahkneb.
Intervallide (-∞,b] ja (-∞, + ∞) valed integraalid on defineeritud sarnaselt:
Defineerime piiramatu funktsiooni integraali mõiste. Kui f(x) on pidev kõigi väärtuste puhul x segment , välja arvatud punkt c, kus f(x) on lõpmatu katkestusega, siis teist tüüpi sobimatu integraal f(x) vahemikus a kuni b summat nimetatakse:
![]()
kui need piirid on olemas ja on lõplikud. Nimetus:
Integraalarvutuste näited
Näide 3.30. Arvutage ∫dx/(x+2).
Lahendus. Tähistame t = x+2, siis dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.
Näide 3.31. Leidke ∫ tgxdx.
Lahendus.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Olgu t=cosx, siis ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.
Näide3.32 . Leidke ∫dx/sinxLahendus.
Näide3.33. Leia .
Lahendus. = .
Näide3.34 . Leidke ∫arctgxdx.
Lahendus. Integreerime osade kaupa. Tähistame u=arctgx, dv=dx. Siis du = dx/(x 2 +1), v=x, kust ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; sest
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.
Näide3.35 . Arvutage ∫lnxdx.
Lahendus. Rakendades integreerimist osade valemiga, saame:
u=lnx, dv=dx, du=1/x dx, v=x. Siis ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.
Näide3.36 . Arvutage ∫e x sinxdx.
Lahendus. Tähistame u = e x, dv = sinxdx, siis du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Samuti integreerime integraali ∫e x cosxdx osade kaupa: u = e x , dv = cosxdx, du=e x dx, v=sinx. Meil on:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Saime seose ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, millest 2∫e x sinx dx = - e x cosx + e x sinx + C.
Näide 3.37. Arvutage J = ∫cos(lnx)dx/x.
Lahendus. Kuna dx/x = dlnx, siis J= ∫cos(lnx)d(lnx). Asendades lnx läbi t, jõuame tabeliintegraalini J = ∫ costdt = sint + C = sin(lnx) + C.
Näide 3.38 . Arvutage J = .
Lahendus. Arvestades, et = d(lnx), asendame lnx = t. Siis J = ![]() .
.
Näide 3.39
. Arvutage integraal J = ![]() .
.
Lahendus. Meil on: ![]() . Seetõttu =
. Seetõttu =
=
=.
sisestatud järgmiselt: sqrt(tan(x/2)).
Ja kui klõpsate tulemuste aknas paremas ülanurgas nuppu Kuva sammud, saate üksikasjaliku lahenduse.
Integraalide lahendamine on lihtne ülesanne, kuid ainult mõne valitud jaoks. See artikkel on mõeldud neile, kes soovivad õppida integraalidest aru saama, kuid ei tea neist midagi või peaaegu mitte midagi. Integraalne... Milleks seda vaja on? Kuidas seda arvutada? Mis on kindlad ja määramata integraalid? Kui ainuke integraali kasutusvõimalus on integraali ikooni kujuline heegelnõel, et raskesti ligipääsetavatest kohtadest midagi kasulikku välja tuua, siis tere tulemast! Siit saate teada, kuidas integraale lahendada ja miks ilma selleta hakkama ei saa.
Uurime mõistet "integraal" Integratsioon oli tuntud juba Vana-Egiptuses. Muidugi mitte tänapäevasel kujul, aga siiski. Sellest ajast peale on matemaatikud sellel teemal palju raamatuid kirjutanud. Eriti silma paistnud Newton Ja Leibniz
, kuid asjade olemus pole muutunud. Kuidas integraalidest nullist aru saada? Mitte mingil juhul! Selle teema mõistmiseks on teil siiski vaja algteadmisi matemaatilise analüüsi põhitõdedest. Integraalide mõistmiseks vajalik teave on meie ajaveebis juba olemas.
Määramatu integraal Olgu meil mingi funktsioon .
f(x) Olgu meil mingi funktsioon Määramatu integraalfunktsioon seda funktsiooni nimetatakse F(x) Olgu meil mingi funktsioon .
, mille tuletis on võrdne funktsiooniga

Kõigi pidevate funktsioonide jaoks on olemas antiderivaat. Samuti lisatakse antiderivaadile sageli konstantmärk, kuna konstandi võrra erinevate funktsioonide tuletised langevad kokku. Integraali leidmise protsessi nimetatakse integreerimiseks.
Lihtne näide:

Et mitte arvutada pidevalt elementaarfunktsioonide antiderivaate, on mugav panna need tabelisse ja kasutada valmisväärtusi.
Täielik integraalide tabel õpilastele

Kindel integraal
Integraali mõiste käsitlemisel on tegemist lõpmata väikeste suurustega. Integraal aitab arvutada figuuri pindala, ebaühtlase keha massi, ebaühtlase liikumise ajal läbitud vahemaa ja palju muud. Tuleks meeles pidada, et integraal on lõpmatult suure hulga lõpmata väikeste liikmete summa.
Kujutage näiteks ette mõne funktsiooni graafikut. Kuidas leida funktsiooni graafikuga piiratud joonise pindala?

Integraali kasutamine! Jagame koordinaattelgede ja funktsiooni graafikuga piiratud kõverjoonelise trapetsi lõpmata väikesteks segmentideks. Nii jagatakse joonis õhukesteks veergudeks. Veergude pindalade summa on trapetsi pindala. Kuid pidage meeles, et selline arvutus annab ligikaudse tulemuse. Kuid mida väiksemad ja kitsamad segmendid, seda täpsem on arvutus. Kui me vähendame neid nii palju, et pikkus kipub nulli, siis segmentide pindalade summa kaldub joonise pindalale. See on kindel integraal, mis on kirjutatud järgmiselt:

Punkte a ja b nimetatakse integratsiooni piirideks.
 Bari Alibasov ja grupp "Integral"
Bari Alibasov ja grupp "Integral" Muide! Meie lugejatele on nüüd 10% allahindlus
Mannekeenide integraalide arvutamise reeglid
Määramata integraali omadused
Kuidas lahendada määramata integraali? Siin vaatleme määramatu integraali omadusi, mis on kasulikud näidete lahendamisel.
- Integraali tuletis on võrdne integrandiga:

- Konstandi saab integraalimärgi alt välja võtta:

- Summa integraal on võrdne integraalide summaga. See kehtib ka erinevuse kohta:
Kindla integraali omadused
- Lineaarsus:

- Integraali märk muutub, kui integreerimise piire vahetatakse:

- Kell ükskõik milline punktid a, b Newton Koos:

Oleme juba teada saanud, et kindel integraal on summa piir. Kuidas aga näite lahendamisel saada konkreetne väärtus? Selleks on Newtoni-Leibnizi valem:

Integraalide lahendamise näited
Allpool vaatleme mitmeid näiteid määramata integraalide leidmisest. Soovitame teil lahenduse keerukusest ise välja mõelda ja kui midagi jääb ebaselgeks, esitage kommentaarides küsimusi.

Materjali tugevdamiseks vaadake videot, kuidas integraale praktikas lahendatakse. Ärge heitke meelt, kui integraali kohe ei anta. Pöörduge üliõpilaste professionaalse teeninduse poole ja kõik kolmik- või kumerad integraalid suletud pinnal on teie võimuses.
Otsene integratsioon
Põhilised integratsioonivalemid
| 1. C – konstant | 1*. | |
| 2. , n ≠ –1 | ||
| 3. +C | ||
| 4. | ||
| 5. | ||
| 6. | ||
| 7. | ||
| 8. | ||
| 9. | ||
| 10. | ||
| 11. | ||
| 12. | ||
| 13. | ||
| 14. |
Integraalide arvutamist lihtintegraalide tabeli ja määramatute integraalide põhiomaduste vahetu kasutamise teel nimetatakse otsene integratsioon.
Näide 1.
Näide 2.
Näide 3.
See on kõige levinum meetod keeruka funktsiooni integreerimiseks, mis seisneb integraali teisendamises, liikudes teisele integratsioonimuutujale.
Kui elementaarteisenduste abil on keeruline integraali taandada tabeliks, siis kasutatakse sel juhul asendusmeetodit. Selle meetodi olemus seisneb selles, et uue muutuja sisseviimisega on võimalik seda integraali taandada uueks integraaliks, mida on suhteliselt lihtne otse võtta.
Asendusmeetodiga integreerimiseks kasutage lahendusskeemi:
2) leida mõlemast varuosast diferentsiaal;
3) väljendab kogu integrandi läbi uue muutuja (mille järel tuleks saada tabeliintegraal);
4) leida saadud tabeliintegraal;
5) teostada pöördvahetus.
Leidke integraalid:
Näide 1 . Asendamine:cosx=t,-sinxdx=dt,
Lahendus:
Näide 2.∫e -x3 x 2 dx Asendamine:-x 3 = t, -3x 2 dx = dt, Lahendus:∫e –x3 x 2 dx=∫e t (-1/3)dt=-1/3e t +C=-1/3e –x3 +C
Näide 3.Asendamine: 1+sinx=t , cosxdx=dt ,
Lahendus: .
JAOTIS 1.5. Määratud integraal, selle arvutamise meetodid.
punkt 1 Kindla integraali mõiste
Ülesanne. Leia funktsiooni juurdekasv, mis on funktsiooni antituletis Olgu meil mingi funktsioon, argumendi läbimisel x väärtusest a väärtustada b.
Lahendus. Oletame, et integratsioon on leidnud: ∫ (x)dx = F(x)+C.
Siis F(x)+C 1, Kus C 1- mis tahes antud arv on selle funktsiooni üks antiderivatiivfunktsioone Olgu meil mingi funktsioon. Leiame selle juurdekasvu, kui argument liigub väärtusest a väärtustada b. Saame:
x=b - x=a =F(b) +C1 - F(a) -C1 =F(b)-F(a)
Nagu näeme, antiderivatiivse funktsiooni suurendamise avaldises F(x)+C 1 püsiv väärtus puudub C 1. Ja kuna all C 1 mis tahes arvu viidata, viib saadud tulemus järgmise järelduseni: argumentide ülemineku kohta x väärtusest x=a väärtustada x=b kõik funktsioonid F(x)+C, antud funktsiooni antiderivaadid Olgu meil mingi funktsioon, on sama juurdekasv võrdne F(b)-F(a).
Seda juurdekasvu nimetatakse tavaliselt kindlaks integraaliks ja tähistatakse sümboliga: ja loetakse: integraal A juurde b funktsioonist f(x) üle dx või lühidalt integraalist A juurde b alates f(x)dx.
Number A helistas alumine piir integratsioon, arv b - üleval; segment a ≤ x ≤ b – integratsiooni segment. Eeldatakse, et integrand funktsioon Olgu meil mingi funktsioon pidev kõigi väärtuste jaoks x, mis vastab järgmistele tingimustele: a x b
Definitsioon. Antiderivatiivsete funktsioonide suurendamine F(x)+C argumentide ülemineku kohta x väärtusest x=a väärtustada x=b, võrdne vahega F(b)-F(a), nimetatakse kindlaks integraaliks ja tähistatakse sümboliga: nii et kui ∫ (x)dx = F(x)+C, siis = F(b)-F(a) – antud võrdsust nimetatakse Newtoni-Leibnizi valemiks.
punkt 2 Kindla integraali põhiomadused
Kõik omadused on sõnastatud väites, et vaadeldavad funktsioonid on integreeritavad vastavatesse intervallidesse.
punkt 3 Kindla integraali otsearvutus
Määratud integraali arvutamiseks, kui leiate vastava määramata integraali, kasutage Newtoni-Leibnizi valemit
need. kindel integraal on võrdne mis tahes antiderivatiivse funktsiooni väärtuste erinevusega integratsiooni ülemisel ja alumisel piiril.
See valem näitab kindla integraali arvutamise protseduuri:
1) leida selle funktsiooni määramatu integraal;
2) asendada saadud antituletisesse argumendi asemel esmalt integraali ülemine ja seejärel alumine piir;
3) lahutab alampiiri asendamise tulemuse ülemise piiri asendamise tulemusest.
Näide 1: Arvutage integraal:
Näide 2: Arvutage integraal:
lk.4 Kindla integraali arvutamine asendusmeetodil
Kindla integraali arvutamine asendusmeetodi abil on järgmine:
1) asendada osa integrandist uue muutujaga;
2) leida kindla integraali uued piirid;
3) leida mõlemast varuosast diferentsiaal;
4) väljendab kogu integrandi läbi uue muutuja (mille järel tuleks saada tabeliintegraal); 5) arvutab saadud kindla integraali.
Näide 1: Arvutage integraal:
Asendamine: 1+cosx=t,-sinxdx=dt,
OSA 1.6. Kindla integraali geomeetriline tähendus.
Kumera trapetsi pindala:
On teada, et lõigul olev kindel integraal tähistab kõverjoonelise trapetsi pindala, mis on piiratud funktsiooni f(x) graafikuga.
Teatud joontega piiratud joonise pindala saab leida teatud integraalide abil, kui nende sirgete võrrandid on teada.
Laske lõigul [a; b] pidev funktsioon on antud y = ƒ(x) ≥ 0. Leiame selle trapetsi pindala.
Joonise pindala, mis on piiratud teljega 0 x, kaks vertikaalset sirget joont x = a, x = b ja funktsiooni y = ƒ(x) graafik (joonis), mis on määratud valemiga:
See on kindla integraali geomeetriline tähendus.
Näide 1: Arvutage joonise pindala, mis on piiratud joontega: y=x2.+2, y=0, x= -2, x=1.
Lahendus: Teeme joonise (pange tähele, et võrrand y=0 defineerib Ox telje).
Vastus: S = 9 ühikut 2
Näide 2: Arvutage joonise pindala, mis on piiratud joontega: y= - e x, x=1 ja koordinaatteljed.
Lahendus: teeme joonise.
Kui kõver trapets asub täielikult Ox telje all, siis selle pindala saab leida järgmise valemi abil:
Sel juhul:
Tähelepanu! Kui teil palutakse leida figuuri pindala kindla integraali abil, siis on pindala alati positiivne! Seetõttu ilmub äsja arutatud valemis miinus.
OSA 1.7. Kindla integraali rakendamine
lk.1 Pöörleva keha ruumala arvutamine
Kui kõverjooneline trapets külgneb Ox-teljega ja sirged y=a, y=b ja funktsiooni graafik y= F(x) (joonis 1), siis määratakse pöördekeha ruumala integraali sisaldava valemiga.
Pöördekeha maht on võrdne:
Näide:
Leidke keha ruumala, mida piirab ümber Ox-telje pöörleva sirge pind 0≤ x ≤4.
Lahendus: V
ühikud 3. Vastus: üksus 3.
JAOTIS 3.1. Tavalised diferentsiaalvõrrandid
punkt 1 Diferentsiaalvõrrandi mõiste
Definitsioon. Diferentsiaalvõrrand on võrrand, mis sisaldab funktsiooni muutujate hulgast ja nende tuletistest.
Sellise võrrandi üldvorm on =0, kus F on selle argumentide teadaolev funktsioon, mis on määratud fikseeritud domeenis; x - sõltumatu muutuja (muutuja, millega seda eristatakse y - sõltuv muutuja (see, millest tuletised võetakse ja mis määratakse); - sõltuva muutuja y tuletis sõltumatu muutuja x suhtes.
punkt 2 Diferentsiaalvõrrandi põhimõisted
järjekorras diferentsiaalvõrrandit nimetatakse selles sisalduva kõrgeima tuletise järguks.
Näiteks:
Teist järku võrrand on esimest järku võrrand.
Nimetatakse mis tahes funktsiooni, mis ühendab muutujaid ja muudab diferentsiaalvõrrandi tõeliseks võrdsuseks otsus diferentsiaalvõrrand.
Üldine lahendus Esimest järku diferentsiaalvõrrandi funktsioon on suvaline konstant C, mis muudab selle võrrandi identiteediks .
Kutsutakse üldlahendust, mis on kirjutatud kaudsel kujul =0 üldine integraal.
Eraotsus võrrand =0 on fikseeritud väärtuse – fikseeritud arvu – üldlahendist saadud lahend.
Konkreetse lahenduse leidmine n-ndat järku diferentsiaalvõrrandile (n= 1,2,3,...), mis vastab vormi algtingimustele
helistas Cauchy probleem.
punkt 3 Eraldatavate muutujatega esimest järku diferentsiaalvõrrandid
Esimest järku diferentsiaalvõrrandit nimetatakse eraldatavaks võrrandiks, kui seda saab esitada kujul, mida saab ümber kirjutada kujul . Kui . Integreerime: .
Seda tüüpi võrrandi lahendamiseks vajate:
1. Eraldi muutujad;
2. Integreerides võrrandi eraldatud muutujatega, leidke selle võrrandi üldlahend;
3. Leia konkreetne lahendus, mis vastab algtingimustele (kui need on antud).
Näide 1. Lahenda võrrand. Leidke konkreetne lahendus, mis vastab tingimusele y=4, kui x=-2.
Lahendus: See on eraldatud muutuja võrrand. Integreerides leiame võrrandi üldlahenduse: . Lihtsama üldlahenduse saamiseks esitame konstantse liikme paremal pool kujul C/2. Meil on või on üldine lahendus. Asendades üldlahendisse väärtused y=4 ja x=-2, saame 16=4+C, millest C=12.
Seega on võrrandi konkreetsel lahendil, mis seda tingimust rahuldab, vorm
Näide 2. Leidke võrrandile konkreetne lahendus, kui .
Lahendus:, , , , , üldlahendus.
Asendame x ja y väärtused privaatse lahendusega: , , privaatlahendus.
Näide 3. Leidke võrrandi üldlahend . Lahendus: ,, , on üldine lahendus.
punkt 4 Esimesest kõrgema järgu diferentsiaalvõrrandid
Vorm või võrrand lahendatakse topeltintegreerimisega: , , kust . Pärast selle funktsiooni integreerimist saame uue funktsiooni f(x), mida tähistame F(x). Seega, ; . Integreerime uuesti: või y=Ф(x). Saime võrrandi üldlahenduse, mis sisaldab kahte suvalist konstanti ja .
Näide 1. Lahenda võrrand.
Lahendus:, , ,
Näide 2. Lahenda võrrand . Lahendus: , , .
JAOTIS 3.2. Numbriseeria, selle liikmed
Definitsioon 1.Numbriseeria nimetatakse väljendiks kujul ++…++…, (1)
Kus , , …, , … - mingisse kindlasse numbrisüsteemi kuuluvad numbrid.
Seega saame rääkida pärissarjadest, mille jaoks R, keeruliste sarjade kohta, mille jaoks C,i= 1, 2, …, n,... = =.
Punkt 3.3. Tõenäosusteooria ja matemaatilise statistika alused
4.1. LIHTSAD INTEGREERIMISMEETODID 4.1.1. Määramatu integraali mõiste
Diferentsiaalarvutuses käsitleti antud funktsiooni tuletise või diferentsiaali leidmise probleemi y= F(x), ehk oli vaja leida f(x)= F"(x) või dF(x)= F"(x)dx= f(x)dx. Esitagem pöördülesanne: taastada diferentseeritud funktsioon, st tuletise tundmine Olgu meil mingi funktsioon(või diferentsiaal f(x)dx), leida selline funktsioon F(x), juurde F"(x)= f(x). See ülesanne osutub palju raskemaks kui eristamise ülesanne. Näiteks olgu teada punkti liikumiskiirus, aga peame leidma seaduse
tema liigutusi S= S(t), ja  Selliste lahendamiseks
Selliste lahendamiseks
ülesandeid, uusi mõisteid ja tegevusi tutvustatakse.
Definitsioon. Diferentseeritav funktsioon seda funktsiooni nimetatakse helistas antiderivaat funktsiooni jaoks f(x) sisse (a; b), Kui F"(x)= f(x) sisse (a; b).
Näiteks selleks f(x) = x 2 antiderivaat  sest
sest
 Sest f(x) = cos x antiderivaat on F(x) = sin x, sest F"(x) = (sin x)" = cos x, mis langeb kokku f(x).
Sest f(x) = cos x antiderivaat on F(x) = sin x, sest F"(x) = (sin x)" = cos x, mis langeb kokku f(x).
Kas antud funktsiooni jaoks on alati antiderivaat olemas? f(x)? Jah, kui see funktsioon on pidevalt sees (a; b). Lisaks on primitiive lugematu arv ja need erinevad üksteisest vaid konstantse liikme poolest. Tõepoolest, patt x+ 2, patt x- 2, patt x+ c- kõik need funktsioonid on cos-i antiderivaadid x(konstantse väärtuse tuletis on 0) - joon. 4.1.
Definitsioon. Väljendus seda funktsiooni nimetatakse+ C, Kus KOOS- suvaline konstantne väärtus, mis määrab funktsiooni antiderivaatide komplekti f(x), helistas määramatu integraal ja seda tähistab sümbol  , st.
, st.  , kus märk on määramatu märk
, kus märk on määramatu märk
lahutamatu, f(x)- helistas integrandi funktsioon, f (x)dx- integrandi poolt x- integratsioonimuutuja.

Riis. 4.1. Integraalkõverate perekonna näide
Definitsioon. Nimetatakse antud tuletisest või diferentsiaalist antiderivaadi leidmise operatsiooni integratsiooni seda funktsiooni.
Integratsioon on diferentseerimise pöördtegevus, seda saab kontrollida diferentseerimisega ja diferentseerimine on ainulaadne ning integratsioon annab vastuse kuni konstantini. Püsiva väärtuse andmine KOOS konkreetsed väärtused  poolt-
poolt-
Saame erinevaid funktsioone
millest igaüks määratleb kõvera koordinaattasandil, mida nimetatakse lahutamatu. Kõik integraalkõverate graafikud nihutatakse piki telge üksteisega paralleelselt Oy. Seetõttu on geomeetriliselt määramatu integraal integraalkõverate perekond.
Niisiis, kasutusele on võetud uued mõisted (antituletis ja määramatu integraal) ja uus tegevus (integratsioon), kuid kuidas ikkagi leida antiderivaat? Sellele küsimusele lihtsaks vastamiseks peate esmalt koostama ja pähe õppima põhiliste elementaarfunktsioonide määramata integraalide tabeli. See saadakse vastavate diferentseerimisvalemite ümberpööramisel. Näiteks kui
Tavaliselt sisaldab tabel mõningaid integraale, mis on saadud pärast kõige lihtsamate integreerimismeetodite rakendamist. Need valemid on tabelis märgitud. 4.1 tähisega “*” ja on tõendatud materjali edasisel esitlusel.
Tabel 4.1. Põhiliste määramata integraalide tabel

Vormel 11 tabelist. 4.1 võib välja näha  ,
,
sest. Sarnane märkus vormi kohta
muulad 13: 

4.1.2. Määramata integraalide omadused
Vaatleme määramatu integraali lihtsamaid omadusi, mis võimaldavad meil integreerida mitte ainult põhilisi elementaarfunktsioone.
1. Määramatu integraali tuletis on võrdne integrandiga:
2. Määramatu integraali diferentsiaal on võrdne integrandiga:
3. Funktsiooni diferentsiaali määramatu integraal on võrdne selle funktsiooniga, mis on lisatud suvalisele konstandile:
Näide 1.  Näide 2.
Näide 2. 
4. Konstantteguri saab integraalimärgist välja võtta: Näide 3. 
5. Kahe funktsiooni summa või erinevuse integraal on võrdne nende funktsioonide integraalide summa või erinevusega:
Näide 4.
Integreerimisvalem jääb kehtima, kui integreerimismuutujaks on funktsioon: if  See
See
Suvaline funktsioon, millel on pidev tuletis. Seda omadust nimetatakse muutumatus.
Näide 5.  , Sellepärast
, Sellepärast
Võrrelge 
Universaalset integratsioonimeetodit pole. Allpool tutvustame mõningaid meetodeid, mis võimaldavad atribuutide 1-5 ja tabeli abil arvutada antud integraali. 4.1.
4.1.3.Otsene integreerimine
See meetod seisneb tabeliintegraalide ja omaduste 4 ja 5 otseses kasutamises. Näited.

4.1.4.Lagundamise meetod
See meetod seisneb integrandi laiendamises juba tuntud integraalidega funktsioonide lineaarseks kombinatsiooniks.
Näited.

4.1.5. Diferentsiaalmärgiga liitumise meetod
Selle integraali taandamiseks tabeliks on mugav teha diferentsiaalteisendusi.
1. Lineaarfunktsiooni diferentsiaalmärgi liitmine
 siit
siit  eelkõige dx =
d(x
+
b),
eelkõige dx =
d(x
+
b),
 diferentsiaal ei muutu, kui muutujale lisada
diferentsiaal ei muutu, kui muutujale lisada
või lahutage konstantne väärtus. Kui muutuja suureneb mitu korda, korrutatakse diferentsiaal selle vastastikuse väärtusega. Näited lahendustega.


Kontrollime tabelist valemeid 9*, 12* ja 14*. 4.1, kasutades diferentsiaalmärgi märkimise meetodit:

Q.E.D.
2. Põhiliste elementaarfunktsioonide liitmine diferentsiaalmärgi alla:



Kommenteeri. Valemeid 15* ja 16* saab kontrollida diferentseerimisega (vt omadus 1). Näiteks

ja see on integrandi funktsioon valemist 16*.
4.1.6. Meetod täiusliku ruudu eraldamiseks ruuttrinoomist
Kui integreerida väljendeid nagu  või
või
 täiusliku ruudu eraldamine ruuttrinoomist
täiusliku ruudu eraldamine ruuttrinoomist
kirves 2 + bx+ c neid on võimalik taandada tabeliteks 12*, 14*, 15* või 16* (vt tabel 4.1).
Kuna üldiselt tundub see toiming keerulisem, kui see tegelikult on, piirdume näidetega.
Näited.
1.
Lahendus. Siin eraldame ruuttrinoomist täiusliku ruudu x 2 + 6x+ 9 = (x 2 + 6x+ 9) - 9 + 5 = (x+ 3) 2 - 4 ja seejärel kasutame diferentsiaalmärgi liitmise meetodit.
Sarnast arutluskäiku kasutades saame arvutada järgmised integraalid:
2. 3.

Integreerimise viimases etapis kasutati valemit 16*.
4.1.7. Põhilised integratsioonimeetodid
Selliseid meetodeid on kaks: muutuja muutmise meetod ehk asendamine ja integreerimine osade kaupa.
Muutuja asendamise meetod
Määramatus integraalis muutuja muutmiseks on kaks valemit:
1) 2)
Siin on sisuliselt monotoonsed diferentseeruvad funktsioonid
nende muutujate kohta.
Meetodi rakendamise kunst seisneb peamiselt funktsioonide valimises nii, et uued integraalid oleksid tabelikujulised või taandavad neile. Lõplik vastus peaks pöörduma tagasi vana muutuja juurde.
Pange tähele, et asendamine diferentsiaalmärgi all on muutuja asendamise erijuht.
Näited.

Lahendus.Siia tuleks sisestada uus muutujatet ruutjuurest lahti saada. Panemex+ 1 = t, Siis x= t 2+ 1 ja dx = 2 tdt:

Lahendus. Asendamine x- 2 per t, saame nimetajas monoomi ja pärast termini kaupa jagamist taandatakse integraal astmefunktsiooni tabeliintegraaliks:



Muutujale üleminekul x kasutatud valemid:
Osade kaupa integreerimise meetod
Kahe funktsiooni korrutise diferentsiaal määratakse valemiga
Selle võrdsuse integreerimisel (vt omadus 3) leiame:

Siit  See on valem integreerimine poolt
See on valem integreerimine poolt
osad.
Osade kaupa integreerimine hõlmab integrandi subjektiivset esitamist vormis u
. dV, ja samal ajal integraal  peaks olema lihtsam kui
peaks olema lihtsam kui  Muidu rakendus
Muidu rakendus
meetodil pole mõtet.
Seega eeldab osade kaupa integreerimise meetod võimet isoleerida tegurid integrandist u Ja dV võttes arvesse ülaltoodud nõudeid.
Esitame rea tüüpilisi integraale, mida saab leida osade kaupa integreerimise meetodil. 1. Vormi integraalid
Kus P(x)- polünoom; k- pidev. Sel juhul u= P(x) ja dV- kõik muud tegurid.
Näide 1.

2. Tüübi integraalid
Siia paneme muud tegurid.
Näide 2.

Näide 3.  Näide 4.
Näide 4.

Iga tulemust saab kontrollida diferentseerimisega. Näiteks antud juhul
Tulemus on õige.
3. Vormi integraalid
kus a, b- konst. Sest u peaks võtma e kirves , patt bx või cos bx.
Näide 5.

Siit saame Näide 6.

Siit

Näide 7.  Näide 8.
Näide 8. 
Lahendus.Siin peate esmalt muutma muutujat ja seejärel integreerima osade kaupa:
Näide 9.  Näide 10.
Näide 10. 
Lahendus. Selle integraali võib leida võrdselt edukalt, asendades muutuja 1 + x 2 = t 2 või integreerides osade kaupa:

Iseseisev töö
Tehke otsene integreerimine (1-10).

Rakendage lihtsaid integreerimismeetodeid (11-46).



Tehke integreerimine muutuja muutmise ja osade abil integreerimise abil (47-74).



 Luminestsents: tüübid, meetodid, rakendused
Luminestsents: tüübid, meetodid, rakendused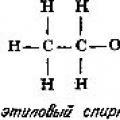 Orgaanilise keemia aluspõhimõtted Orgaaniliste reaktsioonide klassifikatsioon
Orgaanilise keemia aluspõhimõtted Orgaaniliste reaktsioonide klassifikatsioon Erinevus õpetajal ja õpetajal Mis vahe on õpetajal ja õpetajal
Erinevus õpetajal ja õpetajal Mis vahe on õpetajal ja õpetajal