Lecture on the topic: "Trigonometric form of a complex number." Trigonometric form of complex numbers Trigonometric notation of a complex number
3.1. Polar coordinates
Often used on a plane polar coordinate system . It is defined if a point O is given, called pole, and the ray emanating from the pole (for us this is the axis Ox) – polar axis. The position of point M is fixed by two numbers: radius (or radius vector) and angle φ between the polar axis and vector. The angle φ is called polar angle; measured in radians and counted counterclockwise from the polar axis.
The position of a point in the polar coordinate system is given by an ordered pair of numbers (r; φ). At the Pole r = 0, and φ is not defined. For all other points r > 0, and φ is defined up to a term that is a multiple of 2π. In this case, pairs of numbers (r; φ) and (r 1 ; φ 1) are associated with the same point if .
For a rectangular coordinate system xOy The Cartesian coordinates of a point are easily expressed in terms of its polar coordinates as follows:
3.2. Geometric interpretation of complex number
 Let us consider a Cartesian rectangular coordinate system on the plane xOy.
Let us consider a Cartesian rectangular coordinate system on the plane xOy.
Any complex number z=(a, b) is associated with a point on the plane with coordinates ( x, y), Where coordinate x = a, i.e. the real part of the complex number, and the coordinate y = bi is the imaginary part.
A plane whose points are complex numbers is a complex plane.
In the figure, the complex number z = (a, b) corresponds to a point M(x, y).
Exercise.Draw complex numbers on the coordinate plane:
3.3. Trigonometric form of a complex number
A complex number on the plane has the coordinates of a point M(x;y). Wherein:
Writing a complex number ![]() - trigonometric form of a complex number.
- trigonometric form of a complex number.
The number r is called module
complex number z and is designated . Modulus is a non-negative real number. For ![]() .
.
The modulus is zero if and only if z = 0, i.e. a = b = 0.
The number φ is called argument z and is designated. The argument z is defined ambiguously, like the polar angle in the polar coordinate system, namely up to a term that is a multiple of 2π.
Then we accept: , where φ is the smallest value of the argument. It's obvious that
![]() .
.
When studying the topic in more depth, an auxiliary argument φ* is introduced, such that
Example 1. Find the trigonometric form of a complex number.
Solution. 1) consider the module: ;
2) looking for φ: ![]() ;
;
3) trigonometric form: ![]()
Example 2. Find the algebraic form of a complex number ![]() .
.
Here it is enough to substitute the values trigonometric functions and transform the expression:
 Example 3. Find the modulus and argument of a complex number;
Example 3. Find the modulus and argument of a complex number;
1)  ;
;
2) ; φ – in 4 quarters:
3.4. Operations with complex numbers in trigonometric form
· Addition and subtraction It’s more convenient to do with complex numbers in algebraic form:
· Multiplication- with the help of simple trigonometric transformations it can be shown that When multiplying, the modules of numbers are multiplied, and the arguments are added: ;
To determine the position of a point on a plane, you can use polar coordinates [g, (r), Where G is the distance of the point from the origin, and (R- the angle that makes the radius - the vector of this point with the positive direction of the axis Oh. Positive direction of angle change (R The direction considered is counterclockwise. Taking advantage of the connection between Cartesian and polar coordinates: x = g cos avg,y = g sin (p,
we obtain the trigonometric form of writing a complex number
z - r(sin (p + i sin
Where G
Xi + y2, (p is the argument of a complex number, which is found from
l X . y y
formulas cos(p --, sin^9 = - or due to the fact that tg(p --, (p-arctg
Note that when choosing values Wed from the last equation it is necessary to take into account the signs x and y.
Example 47. Write a complex number in trigonometric form 2 = -1 + l/Z / .
Solution. Let's find the modulus and argument of a complex number:
= yj 1 + 3 = 2 . Corner Wed we find from the relations cos(p = -, sin(p = - . Then
we get cos(p = -,suup
u/z g~
- - -. Obviously, the point z = -1 + V3-/ is located
- 2 To 3
in the second quarter: (R= 120°
Substituting
2 k.. cos--h; sin
into formula (1) found 27Г L
Comment. The argument of a complex number is not uniquely defined, but to within a term that is a multiple of 2p. Then through sp^g denote
argument value enclosed within (p 0 %2 Then
A)^g = + 2kk.
Using the famous Euler formula e, we obtain the exponential form of writing a complex number.
We have r = g(co^(p + i?,p(p)=ge,
Operations on complex numbers
- 1. The sum of two complex numbers r, = X] + y x/ and g 2 - x 2 +y 2 / is determined according to the formula r! +2 2 = (x, +^2) + (^1 + ^2)‘ r
- 2. The operation of subtracting complex numbers is defined as the inverse operation of addition. Complex number g = g x - g 2, If g 2 + g = g x,
is the difference of complex numbers 2, and g 2. Then r = (x, - x 2) + (y, - at 2) /.
- 3. Product of two complex numbers g x= x, +y, -z and 2 2 = x 2+ U2‘ r is determined by the formula
- *1*2 =(* +U"0(X 2+ T 2 -0= X 1 X 2 Y 1 2 -1 +x Y2 " * + U1 U2 " ^ =
= (хх 2 ~УУ 2)+(Х У2 + Х 2У)-"-
In particular, y-y= (x + y-y)(x-y /)= x 2 + y 2.
You can obtain formulas for multiplying complex numbers in exponential and trigonometric forms. We have:
- 1^ 2 - G x e 1 = )G 2 e > = G]G 2 cOs((P + avg 2) + isin
- 4. Division of complex numbers is defined as the inverse operation
multiplication, i.e. number G-- called the quotient of division r! on g 2,
If g x -1 2 ? 2 . Then
X + Ti _ (*і + IU 2 ~ 1 U2 ) x 2 + ІУ2 ( 2 + ^У 2)( 2 ~ 1 У 2)
x, x 2 + /y, x 2 - ix x y 2 - i 2 y x y 2 (x x x 2 + y x y 2)+ /(- x,y 2 + X 2 Y])
2 2 x 2 + Y 2
1 e
i(r g
- - 1U e "(1 Fg) - I.сОї((Р -ср 1)+ І- (R-,)] >2 >2
- 5. Raising a complex number to a positive integer power is best done if the number is written in exponential or trigonometric forms.
Indeed, if g = ge 1 then
=(ge,) = g p e t = G"(co8 psr+іт gkr).
Formula g" =r n (cosn(p+is n(p) called Moivre's formula.
6. Root extraction P- th power of a complex number is defined as the inverse operation of raising to a power p, p- 1,2,3,... i.e. complex number = y[g called a root P- th power of a complex number
g, if G = g x. From this definition it follows that g - g", A g x= l/g. (r-psr x, A sr^-sr/p, which follows from Moivre’s formula written for the number = r/*+ іьіпп(р).
As noted above, the argument of a complex number is not uniquely defined, but up to a term that is a multiple of 2 and. That's why = (p + 2pk, and the argument of the number r, depending on To, let's denote (r k and boo
dem calculate using the formula (r k= - + . It is clear that there is P com-
complex numbers, P-th power of which is equal to the number 2. These numbers have one
and the same module equal y[g, and the arguments of these numbers are obtained by To = 0, 1, P - 1. Thus, in trigonometric form root i-th degrees are calculated using the formula:
(p + 2kp . . Wed + 2kp
, To = 0, 1, 77-1,
.(p+2ktg
and in exponential form - according to the formula l[g - y[ge p
Example 48. Perform operations on complex numbers in algebraic form:
a) (1-/H/2) 3 (3 + /)
- (1 - /l/2) 3 (z + /) = (1 - zl/2/ + 6/ 2 - 2 l/2 / ? 3)(3 + /) =
- (1 - Zl/2/ - 6 + 2l/2/DZ + /)=(- 5 - l/2/DZ + /) =
15-Zl/2/-5/-l/2/ 2 = -15 - Zl/2/-5/+ l/2 = (-15 +l/2)-(5 +Zl/2)/;
Example 49. Raise the number r = Uz - / to the fifth power.
Solution. We obtain the trigonometric form of writing the number r.
G = l/3 + 1 =2, C08 (p --, 5ІІ7 (R =
- (1 - 2/X2 + /)
- (z-,)
O - 2.-X2 + o
- 12+ 4/-9/
- 2 +і - 4/ - 2/ 2 2 - 3/ + 2 4 - 3/ 3 + і
- (z-O " (z-O
Z/ 2 12-51 + 3 15 - 5/
- (3-i) ’з+/
- 9 + 1 z_±.
- 5 2 1 "
From here O--, A r = 2
We get Moivre: i -2
/ ^ _ 7G, . ?G
- -SS-- ІБІП -
- --b / -
= -(l/w + g)= -2 .
Example 50: Find all values
Solution, r = 2, a Wed we find from the equation sob(p = -,zt--.
This point 1 - /d/z is located in the fourth quarter, i.e. f =--. Then
- 1 - 2
- ( ( UG L
We find the root values from the expression
V1 - /l/z = l/2
- --+ 2А:/г ---ь 2 kk
- 3 . . 3
S08--1- and 81P-
At To - 0 we have 2 0 = l/2
You can find the values of the root of the number 2 by representing the number in the display
-* TO/ 3 + 2 cl
At To= 1 we have another root value:
- 7G. 7G_
- ---ь27г ---ь2;г
- 3. . h
7G . . 7G L-С05- + 181П - 6 6
- --N-
co? - 7G + /5SH - I"
l/3__t_
telial form. Because r= 2, a Wed= , then g = 2e 3 , a y[g = y/2e 2
Operations on complex numbers written in algebraic form
Algebraic form of a complex number z =(a,b).is called an algebraic expression of the form
z = a + bi.
Arithmetic operations on complex numbers z 1 = a 1 +b 1 i And z 2 = a 2 +b 2 i, written in algebraic form, are carried out as follows.
1. Sum (difference) of complex numbers
z 1 ±z 2 = (a 1 ± a 2) + (b 1 ±b 2)∙i,
those. addition (subtraction) is carried out according to the rule for adding polynomials with reduction of similar terms.
2. Product of complex numbers
z 1 ∙z 2 = (a 1 ∙a 2 - b 1 ∙b 2) + (a 1 ∙b 2 + a 2 ∙b 1)∙i,
those. multiplication is carried out according to the usual rule for multiplying polynomials, taking into account the fact that i 2 = 1.
3. The division of two complex numbers is carried out according to the following rule:
, (z 2 ≠ 0),
those. division is carried out by multiplying the dividend and the divisor by the conjugate number of the divisor.
Exponentiation of complex numbers is defined as follows:
It is easy to show that

Examples.
1. Find the sum of complex numbers z 1 = 2 – i And z 2 = – 4 + 3i.
z 1 + z 2 = (2 + (–1)∙i)+ (–4 + 3i) = (2 + (–4)) + ((–1) + 3) i = –2+2i.
2. Find the product of complex numbers z 1 = 2 – 3i And z 2 = –4 + 5i.
= (2 – 3i) ∙ (–4 + 5i) = 2 ∙(–4) + (-4) ∙(–3i)+ 2∙5i– 3i∙ 5i = 7+22i.
3. Find the quotient z from division z 1 = 3 – 2na z 2 = 3 – i.
z = .
4. Solve the equation: , x And y Î R.
(2x+y) + (x+y)i = 2 + 3i.
Due to the equality of complex numbers we have:
where x =–1 , y= 4.
5. Calculate: i 2 ,i 3 ,i 4 ,i 5 ,i 6 ,i -1 ,i -2 .

6. Calculate if .
![]() .
.
7. Calculate the reciprocal of a number z=3-i.
Complex numbers in trigonometric form
Complex plane called a plane with Cartesian coordinates ( x, y), if each point with coordinates ( a, b) is associated with a complex number z = a + bi. In this case, the abscissa axis is called real axis, and the ordinate axis is imaginary. Then every complex number a+bi geometrically depicted on a plane as a point A (a, b) or vector.
Therefore, the position of the point A(and, therefore, a complex number z) can be specified by the length of the vector | | = r and angle j, formed by the vector | | with the positive direction of the real axis. The length of the vector is called modulus of a complex number and is denoted by | z |=r, and the angle j called complex number argument and is designated j = arg z.
It is clear that | z| ³ 0 and | z | = 0 Û z = 0.
From Fig. 2 it is clear that .
The argument of a complex number is determined ambiguously, but with an accuracy of 2 pk, kÎ Z.
From Fig. 2 it is also clear that if z=a+bi And j=arg z, That
cos j =,sin j =, tg j = .
If zÎR And z> 0,then arg z = 0 +2pk;
If z ОR And z< 0,then arg z = p + 2pk;
If z = 0,arg z indefined.
The main value of the argument is determined on the interval 0 £ arg z£2 p,
or -p£ arg z £ p.
Examples:
1. Find the modulus of complex numbers z 1 = 4 – 3i And z 2 = –2–2i.
2. Define areas on the complex plane defined by the conditions:
1) | z | = 5; 2) | z| £6; 3) | z – (2+i) | £3; 4) £6 | z – i| £7.
Solutions and answers:
1) | z| = 5 Û Û - equation of a circle with radius 5 and center at the origin.
2) A circle with radius 6 with center at the origin.
3) Circle with radius 3 with center at point z 0 = 2 + i.
4) A ring bounded by circles with radii 6 and 7 with a center at a point z 0 = i.
3. Find the modulus and argument of the numbers: 1) ; 2) .
1) ; A = 1, b = Þ ![]() ,
,
 Þ j 1 =
Þ j 1 = ![]() .
.
2) z 2 = –2 – 2i; a =–2, b =-2 Þ ![]() ,
,
 .
.
Hint: When determining the main argument, use the complex plane.
Thus: z 1 = .
2) ![]() , r 2 =
1, j 2 = ,
, r 2 =
1, j 2 = , ![]() .
.
3) ![]() , r 3 = 1, j 3 = ,
, r 3 = 1, j 3 = , ![]() .
.
4) , r 4 = 1, j 4 = , ![]() .
.
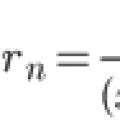 Taylor series expansion Approximate solution of the Cauchy problem for the ordinary
Taylor series expansion Approximate solution of the Cauchy problem for the ordinary What is NOT taught at school What is not taught at school ask
What is NOT taught at school What is not taught at school ask Money Thinking Formula (A
Money Thinking Formula (A