The equation of motion of the center of mass of the system has the form. Equation of motion of the center of mass
When we are dealing with a system of particles, it is convenient to find a point - the center of mass - that would characterize the position and movement of this system as a whole. In a system of two identical particles, such a point C obviously lies in the middle between them (Fig. 110a). This is clear from considerations of symmetry: in a homogeneous and isotropic space, this point is distinguished from all others, because for any other point A located closer to one of the particles, there is a point B symmetrical to it, located closer to the second particle.
Rice. 110. The center of mass of two identical particles is at point C with radius vector ; the center of mass of two particles with different masses divides the segment between them in a ratio inversely proportional to the masses of the particles (b)
Obviously, the radius vector of point C is equal to half the sum of the radius vectors of identical particles (Fig. 110a): In other words, it is the usual average value of the vectors
Determination of the center of mass. How to generalize this definition to the case of two particles with different masses It can be expected that, along with the geometric center of the system, the radius vector of which is still equal to half the sum, a point will play a certain role, the position of which is determined by the distribution
I eat mass. It is natural to define it so that the contribution of each particle is proportional to its mass:
![]()
The radius vector of the center of mass, determined by formula (1), is the weighted average value of the radius vectors of particles, which is obvious if we rewrite (1) in the form
![]()
The radius vector of each particle enters with a weight proportional to its mass. It is easy to see that the center of mass C, determined by formula (1), lies on the straight line segment connecting the particles and divides it in a ratio inversely proportional to the masses of the particles: (Fig. 110b).
Please note that the definition of the center of mass given here is related to the condition of equilibrium of the lever, which you know. Let us imagine that point masses, which are subject to the action of a uniform gravitational field, are connected by a rod of negligible mass. Such a lever will be in equilibrium if its fulcrum is placed at the center of mass C.
A natural generalization of formula (1) to the case of a system consisting of material points with masses and radius vectors is the equality
which serves as a definition of the radius vector of the center of mass (or center of inertia) of the system.
Speed of the center of mass. The center of mass characterizes not only the position, but also the movement of the system of particles as a whole. The velocity of the center of mass, determined by the equality as follows from (2), is expressed as follows in terms of the velocities of the particles forming the system:

The numerator on the right side of this expression, as follows from formula (6) of the previous paragraph, contains the total momentum of the system P, and the denominator is its total mass M. Therefore, the momentum of a particle system is equal to the product of the mass of the entire system M and the speed of its center of mass

Formula (4) shows that the momentum of a system is related to the velocity of its center of mass in the same way as the momentum of an individual particle is related to the velocity of the particle. It is in this sense that the movement of the center of mass characterizes the movement of the system as a whole.
Law of motion of the center of mass. The law of change in the momentum of a system of particles, expressed by formula (9) of the previous paragraph, is essentially the law of motion of its center of mass. In fact, from (4) with a constant total mass M of the system we have
![]()
which means that the rate of change of momentum of the system is equal to the product of its mass and the acceleration of the center of mass. Comparing (5) with formula (6) § 29, we obtain

According to (6), the center of mass of the system moves as one material point of mass M would move under the influence of a force equal to the sum of all external forces acting on the particles entering the system. In particular, the center of mass of a closed physical system, which is not acted upon by external forces, moves uniformly and rectilinearly in the inertial frame of reference or is at rest.
The idea of the center of mass in a number of cases makes it possible to obtain answers to some questions even more simply than by directly using the law of conservation of momentum. Consider the following example.
An astronaut outside the ship. A mass cosmonaut, stationary relative to the mass spacecraft with the engine turned off, begins to pull himself towards the ship using a light safety cord. What distances will the astronaut and the spacecraft travel before meeting if the initial distance between them is
The center of mass of the ship and the astronaut is located on the straight line connecting them, and the corresponding distances are inversely proportional to the masses. Since then
we get it right away
![]()
In deep space, where there are no external forces, the center of mass of this closed system is either at rest or moving at a constant speed. In the reference frame where he is at rest, the astronaut and the ship will travel the distances given by formulas (7) before meeting.
For the validity of such reasoning, it is fundamentally important to use an inertial frame of reference. If here we had recklessly connected the reference system with the spaceship, we would have come to the conclusion that when the astronaut is pulled up, the center of mass of the system begins to move in the absence of external forces: he approaches the ship. The center of mass maintains its speed only relative to the inertial reference frame.
Equation (6), which determines the acceleration of the center of mass of a particle system, does not include the internal forces acting in it. Does this mean that internal forces have no effect on the movement of the center of mass at all? In the absence of external forces or when these forces are constant, this is indeed the case. For example, in a uniform field of gravity, the center of mass of a projectile that exploded in flight continues to move along the same parabola until none of the fragments have yet fallen to the ground.
The role of internal forces. In cases where external forces can change, the situation is somewhat more complicated. External forces act not on the center of mass, but on individual particles of the system. These forces can depend on the position of the particles, and the position of each particle during its movement is determined by all the forces acting on it, both external and internal.
Let us explain this using the same simple example of a projectile that breaks into small fragments in flight under the influence of internal forces. While all the fragments are in flight, the center of mass, as already mentioned, continues to move along the same parabola. However, as soon as at least one of the fragments touches the ground and its movement stops, a new external force will be added - the reaction force of the earth's surface acting on the fallen fragment. As a result, the acceleration of the center of mass will change, and it will no longer move along the same parabola. The very appearance of this reaction force is a consequence of the action of internal forces that exploded the projectile. So, the action of internal forces at the moment the projectile breaks can lead to a change in the acceleration with which the center of mass will move at later times and, consequently, to a change in its trajectory.
Let us give an even more striking example of the influence of internal forces on the movement of the center of mass. Let's imagine that the Earth's satellite,
revolving around it in a circular orbit, under the influence of internal forces it is divided into two halves. One of the halves stops and begins to fall vertically to the Earth. According to the law of conservation of momentum, the second half must at this moment double its speed, directed tangentially to the circle. As we will see below, at such a speed this half will fly away from the Earth to an infinitely large distance. Consequently, the center of mass of the satellite, i.e., its two halves, will also move to an infinitely large distance from the Earth. And the reason for this is the action of internal forces when the satellite is divided into two parts, since otherwise the undivided satellite would continue to move in a circular orbit.
Jet propulsion. The law of conservation of momentum of a closed system makes it easy to explain the principle of reactive motion. When fuel is burned, the temperature rises and high pressure is created in the combustion chamber, due to which the resulting gases escape from the rocket engine nozzle at high speed. In the absence of external fields, the total momentum of the rocket and the gases escaping from the nozzle remains unchanged. Therefore, when the gases flow out, the rocket acquires speed in the opposite direction.
Meshchersky equation. We obtain an equation describing the motion of the rocket. Let at some moment of time the rocket in some inertial frame of reference have a speed. Let us introduce another inertial frame of reference, in which at a given moment of time the rocket is stationary. Let us call such a reference system comoving. If a working rocket engine ejects mass gases at a speed relative to the rocket over a period of time, then after a while the rocket’s speed in this accompanying system will be different from zero and equal to
Let us apply the law of conservation of momentum to the closed physical system under consideration, a rocket plus gases. At the initial moment, in the accompanying frame of reference, the rocket and gases are at rest, so the total momentum is zero. After time, the momentum of the rocket is equal to the momentum of the ejected gases. Therefore
The total mass of the rocket system plus gases is conserved, so the mass of ejected gases is equal to the loss of rocket mass:
![]()
Now equation (8) after dividing by a period of time is rewritten as
![]()
Moving to the limit, we obtain the equation of motion of a body of variable mass (rocket) in the absence of external forces:
![]()
Equation (9) has the form of Newton’s second law, if its right side is considered as a reactive force, i.e., the force with which the gases escaping from it act on the rocket. The mass of the rocket here is not constant, but decreases over time due to the loss of matter, i.e. Therefore, the reactive force; directed in the direction opposite to the speed of the gases escaping from the nozzle relative to the rocket. It can be seen that this force is greater, the higher the speed of gas flow and the higher the fuel consumption per unit time.
Equation (9) was obtained in a certain inertial reference system - the accompanying system. Due to the principle of relativity, it is also true in any other inertial frame of reference. If, in addition to the reactive force, any other external forces act on the rocket, such as gravity and air resistance, then they should be added to the right side of equation (9):
![]()
This equation was first obtained by Meshchersky and bears his name. For a given engine operating mode, when the mass is a certain known function of time, the Meshchersky equation allows you to calculate the speed of the rocket at any time.
What physical considerations indicate the advisability of determining the center of mass using formula (1)?
In what sense does the center of mass characterize the movement of a system of particles as a whole?
What does the law of motion of the center of mass of a system of interacting bodies say? Do internal forces affect the acceleration of the center of mass?
Can internal forces influence the trajectory of the system's center of mass?
In the problem of a projectile bursting, considered in the previous paragraph, the law of motion of the center of mass allows us to immediately find the flight range of the second fragment if its initial speed is horizontal. How to do it? Why do these considerations not apply in the case where its initial velocity has a vertical component?
During the acceleration of a rocket, its engine operates in a constant mode, so that the relative speed of gas flow and fuel consumption per unit time are unchanged. Will the acceleration of the rocket be constant?
Derive the Meshchersky equation using, instead of a comoving reference frame, an inertial frame in which the rocket already has speed
Tsiolkovsky's formula. Let us assume that the rocket accelerates in free space, where no external forces act on it. As fuel is consumed, the mass of the rocket decreases. Let's find the relationship between the mass of fuel consumed and the speed gained by the rocket.
After turning on the engine, the stationary rocket begins to pick up speed, moving in a straight line. Projecting the vector equation (9) onto the direction of motion of the rocket, we obtain
![]()
In equation (11), we will consider the mass of the rocket as a function of the speed gained by the rocket. Then the rate of change of mass over time can be represented as follows:
![]()
Dot WITH, the position of which is determined by the radius vector:
called center of mass systems of material points. Here m i- weight i th particle; r i- radius vector specifying the position of this particle; - total mass of the system. (Note that in a uniform field of gravity, the center of mass coincides with the center of gravity of the system.)
Having differentiated r C in time, we find the speed of the center of mass:
Where V i- speed i-th material point, p i- her impulse, P – momentum of the system of material points. From (2.18) it follows that the total momentum of the system is
P = m V C, (2.19)
From (2.19) and (2.16), we obtain the equation of motion of the center of mass:
(A C– acceleration of the center of mass). Thus, from Eq.
it follows that the center of mass moves in the same way as a material point with a mass equal to the mass of the system would move under the action of the resultant of all external forces applied to the bodies of the system. For a closed system and C = 0. This means that the center of mass of a closed system moves rectilinearly and uniformly or is at rest.
The reference system relative to which the center of mass is at rest is called center of mass system(abbreviated ts- system). This system is inertial.
Control questions
1. In what frames of reference are Newton’s laws valid?
2. What formulations of Newton’s second law do you know?
3. What is the weight of a freely falling body?
4. What is the sign of the scalar product of the friction force and the velocity of the body?
5. What is the momentum of the system of material points in the center of mass system?
6. What is the acceleration of the center of mass of a body having mass m and under the influence of forces?
1. A bullet pierces two adjacent boxes of liquids: first a box with glycerin, then the same box with water. How will the final velocity of the bullet change if the boxes are swapped? Other forces acting on a bullet other than fluid resistance F = – r V , neglect.
2. The motion of a material point is given by the equations x = a t 3 , y = b t.
3. The speed of a material point is given by the equations u x = A ∙ sinw t,u y = A ∙ cosw t. Does the force acting on a point change: a) in magnitude; b) in the direction?
4. A ball hanging on a thread long l, after a horizontal push rises to a height H without leaving the circle. Can its speed be equal to zero: a) when H< l b) when H>l?
5. Two bodies with masses T 1 > m 2 fall from the same height. The resistance forces are considered constant and identical for both bodies. Compare the time of falling bodies.
6. Two identical bars connected by a thread move along a horizontal plane under the action of a horizontal force F . Does the tension force of the thread depend on: a) the mass of the bars; b) on the coefficient of friction between the bars and the plane?
7. Block of mass m 1 = 1 kg rests on a block of mass m 2 = 2 kg. A horizontal force began to act on the lower block, increasing in proportion to time, its modulus F= 3t(F– in N, t– in c). At what point in time will the top block begin to slip? The coefficient of friction between the bars is m = 0.1, the friction between the lower bar and the support is negligible. Accept g= 10 m/s 2.
8. Two balls a and b, suspended on threads at a common point 0, move uniformly along circular trajectories lying in the same horizontal plane. Compare their angular velocities.
9. A conical funnel rotates at a constant angular velocity w. Inside the funnel on the wall lies a body that can slide freely along the generatrix of the cone. During rotation, the body is in equilibrium relative to the wall. Is this equilibrium stable or unstable?
Chapter 3
Work and Energy
Let's assume that we have a certain system consisting of n number of material points. Let's take one of them and denote its mass as m k. External forces applied to a point (both active forces and coupling reactions) have a resultant F k e . Internal forces have a resultant F k l . Our system is in motion, therefore, the desired point will have an acceleration a k. Knowing the basic law of dynamics, we can write the following formula:
m k a k = F k e + F k l .
It can be applied to any point in the system. This means that for the entire system we can formulate the following equations:
m 1 a 1 = F 1 e + F 1 l, m 2 a 2 = F 2 e + F 2 l, ⋯ m n a n = F n e + F n l.
This formula consists of differential equations that describe the motion of the system in vector form. If we project these equalities onto the corresponding coordinate axes, then we will obtain differential equations of motion in projections. But in specific problems, most often it is not necessary to calculate the movement of each point of the system: you can limit yourself to the characteristics of the movement of the entire system as a whole.
Motion of the center of mass: main theorem
The nature of the motion of a system can be determined by knowing the law according to which its center of mass moves.
Definition 1
Center of inertia of the system (center of mass) is an imaginary point with a radius vector R, expressed in terms of radius vectors r 1, r 2, . . . corresponding material points according to the formula R = m 1 r 1 + m 2 r 2 + . . . + m n r n m .
Here the sum of the indicators in the numerator m = m 1 + m 2 +. . . + m 3 expresses the total mass of the entire system.
To find this law, we need to take the equations of motion of the system given in the previous paragraph and add their right and left sides. What we get is:
∑ m k a k ¯ = ∑ F k ¯ e + ∑ F k ¯ l .
Taking the formula for the radius vector of the center of mass, we get the following:
∑ m k r k = M r c .
Now let's take the second derivative with respect to time:
∑ m k a k = M a c .
Here the letter a c ¯ denotes the acceleration acquired by the center of mass of the system.
Definition 2
The property of internal forces in the system states that F k l is equal to zero, which means the final equality will look like this:
M a c ¯ = ∑ F k ¯ e .
This equation is written law of motion of the center of mass. Let's write it down:
The movement of the center of mass of the system is identical to the movement of a material point of the same mass as the entire system, to which all external forces acting on the system are applied.
In other words, the product of the acceleration of the center of mass of the system and the mass of the system itself will be equal to the geometric sum of all external forces acting on this system.
Let's take the equation obtained above and project its right and left sides onto the corresponding coordinate axes. We will get:
M x c ¨ = ∑ F k x ¯ e , M y c ¨ = ∑ F k y ¯ e , M z c ¨ = ∑ F k z ¯ e .
These equalities are differential equations of motion of the center of mass in projection onto the axis in the Cartesian coordinate system.
This theorem has great practical value. Let us explain what exactly it is.
Theorem 1
- Any body moving translationally can be considered as a material point, the mass of which is equal to the mass of the entire body. In all other cases, such an approach is possible only when, to determine the position of the body in space, it is enough for us to know in what position its center of mass is located. It is also important that the conditions of the problem allow the exclusion of the rotational part of the body movement.
- Using the theorem of motion of the center of mass of the system, we can not consider internal forces unknown to us in advance in problems.
Let's look at an example of applying the theorem to solve a practical problem.
Example 1
Condition: A metal ring is suspended from the axis of the centrifugal machine by a thread. It performs uniform rotational movements with an angular velocity equal to ω. Calculate how far the center of the ring is from the axis of rotation.
Solution
It is obvious that the system is under the influence of gravity N N ¯ α α . It is also necessary to take into account the tension of the thread and centripetal acceleration.
Newton's second law for the system will look like this:
m a ¯ = N ¯ + m g ¯ .
Now let’s create projections of both sides of the equality on the abscissa and ordinate axes and get:
N sin α = m a ; N cos α = m g .
We can divide one equation by another:
Since a = υ 2 R, υ = ω R, the equation we need will look like this:
R = g t g α ω 2 .
Answer: R = g t g α ω 2 .
If you notice an error in the text, please highlight it and press Ctrl+Enter
Differential equations of system motion
Let us consider a system consisting of $n$ material points. Let us select some point of the system with mass $m_(k).$ We denote the resultant of all external forces applied to the point (both active and constraint reactions) by $\overline(F)_(k)^(e) $, and the resultant all internal forces - through $\overline(F)_(k)^(l) $. If the point has an acceleration $\overline(a_(k) )$, then according to the basic law of dynamics:
We get a similar result for any point. Therefore, for the entire system it will be:
Equations (1) are differential equations of motion of the system in vector form.
Projecting equalities (1) onto the coordinate axes, we obtain the equations of motion of the system in differential form in projections onto these axes.
However, when solving many specific problems, the need to find the law of motion for each of the points of the system does not arise, but sometimes it is enough to find the characteristics that determine the motion of the entire system as a whole.
Theorem on the motion of the center of mass of the system
To determine the nature of the motion of a system, it is necessary to know the law of motion of its center of mass. The center of mass or center of inertia of a system is such an imaginary point, the radius vector $R$ of which is expressed through the radius vectors $r_(1) ,r_(2) ,...$of material points according to the formula:
$R=\frac(m_(1) r_(1) +m_(2) r_(2) +...+m_(n) r_(n) )(m) $, (2)
where $m=m_(1) +m_(2) +...+m_(n) $ is the total mass of the entire system.
To find this law, let us turn to the equations of motion of system (1) and add their left and right sides term by term. Then we get:
$\sum m_(k) \overline(a)_(k) =\sum \overline(F)_(k)^(e) +\sum \overline(F)_(k)^(l) $. (3)
From formula (2) we have:
Taking the second derivative with respect to time, we get:
$\sum m_(k) \overline(a)_(k) =M\overline(a)_(c) $, (4)
where $\overline(a)_(c) $ is the acceleration of the center of mass of the system.
Since, by the property of internal forces in the system, $\sum \overline(F)_(k)^(l) =0$, we finally obtain from equality (3), taking into account (4):
$M\overline(a)_(c) =\sum \overline(F)_(k)^(e) $. (5)
Equation (5) expresses the theorem on the motion of the center of mass of the system: the product of the mass of the system and the acceleration of its center of mass is equal to the geometric sum of all external forces acting on the system, or the center of mass of the system moves like a material point, the mass of which is equal to the mass of the entire system and to which all external forces are applied forces acting on the system.
Projecting both sides of equality (5) onto the coordinate axes, we obtain:
$M\ddot(x)_(c) =\sum \overline(F)_(kx)^(e) $, $M\ddot(y)_(c) =\sum \overline(F)_( ky)^(e) $, $M\ddot(z)_(c) =\sum \overline(F)_(kz)^(e) $. (6)
These equations are differential equations of motion of the center of mass in projections on the axes of the Cartesian coordinate system.
The meaning of the theorem is as follows:
Theorem
- A forward moving body can always be considered as a material point with a mass equal to the mass of the body. In other cases, the body can be considered as a material point only when, in practice, to determine the position of the body it is enough to know the position of its center of mass and it is permissible, according to the conditions of the problem, not to take into account the rotational part of the body’s movement;
- The theorem allows us to exclude from consideration all previously unknown internal forces. This is its practical value.
Example
A metal ring suspended on a thread to the axis of a centrifugal machine rotates uniformly with an angular velocity $\omega $. The thread makes an angle $\alpha $ with the axis. Find the distance from the center of the ring to the axis of rotation.
\[\omega \] \[\alpha \]
Our system is affected by the force of gravity $\overline(N)$ $\overline(N)$ $\alpha \alpha$, the tension force of the thread and centripetal acceleration.
Let's write down Newton's second law for our system:
Let's project both parts onto the x and y axes:
\[\left\( \begin(array)(c) N\sin \alpha =ma; \\ N\cos \alpha =mg; \end(array) \right.(4)\]
Dividing one equation by the other, we get:
Since $a=\frac(v^(2) )(R) ;$$v=\omega R$, we find the required distance:
Answer: $R=\frac(gtg\alpha )(\omega ^(2) ) $
A MECHANICAL SYSTEM is an arbitrary pre-selected set of material bodies whose behavior is analyzed.
In the future, the following rule will be used: IN MATHEMATICAL CALCULATIONS, THE CHARACTERISTICS OF MATERIAL POINTS, IN CONDITION TO THE CHARACTERISTICS OF MATERIAL BODIES, WILL HAVE AN INDEX.
BODY MASS is the sum of the masses of all material points that make up a given body
EXTERNAL FORCES are the forces of interaction between material points included in a mechanical system and not included.
INTERNAL FORCES are the forces of interaction between material points included in a mechanical system.
THEOREM D1. The sum of the internal forces of a mechanical system is always zero.
Proof. According to axiom D5, for any pair of material points of a mechanical system, the sum of their interaction forces is always equal to zero. But all interacting points belong to the system and, therefore, for any of the internal forces there will always be an opposing internal force. Therefore, the total sum of all internal forces is necessarily zero. Etc.
THEOREM D2.The sum of the moments of internal forces of a mechanical system is always equal to zero.
Proof. According to axiom D5, for every internal force there is an opposing internal force. Since the lines of action of these forces coincide, their shoulders relative to any point in space will be the same and, therefore, their moments relative to the selected point in space are the same in magnitude, but the signs are different, since the forces are directed in the opposite direction. Therefore, the total sum of the moments of all internal forces is necessarily zero. Etc.
THEOREM D3.The product of the mass of the entire mechanical system and the acceleration of its center of mass is equal to the sum of all external forces acting on the system.
Proof. Let us consider an arbitrary mechanical system consisting of a finite number of material bodies. Based on axiom D2, we can divide each body into a finite number of material points. Let everything be received n such points. For each such point, based on axiom D4, we can create an equation of motion
Considering that  (KINEMATICS p. 3), as well as breaking down all the forces acting on i th point, into external and internal, we obtain from the previous equality
(KINEMATICS p. 3), as well as breaking down all the forces acting on i th point, into external and internal, we obtain from the previous equality

If we sum up the equations of motion of all points of the system, we get

Using the commutativity of the operations of summation and differentiation (in fact, the signs of summation and differentiation can be swapped), we obtain
 (40)
(40)
The expression obtained in brackets can be represented through the coordinate of the center of mass of the system (STATICS p. 15)

Where m– mass of the entire system;
Radius vector of the system's center of mass.
As follows from Theorem D1, the last term in expression (40) vanishes, therefore

or  , etc. (41)
, etc. (41)
Consequence. The center of mass of a mechanical system moves as if it were a material point possessing the entire mass of the system and to which all external forces are reduced.
Movement of a mechanical system in the absence of external forces
Theorem D4. If the external forces acting on a mechanical system are balanced in a certain direction, then the center of mass of the system in this direction will move at a constant speed.
Proof X coincided with the direction in which external forces are balanced, i.e. sum of projections of external forces onto the axis X equal to zero

Then, according to Theorem D3
Since, therefore
If we integrate the last expression, we get
THEOREM D5. If the external forces acting on a mechanical system are balanced in a certain direction and at the initial moment the system was at rest, then the center of mass of the system remains motionless throughout the movement.
Proof. Repeating the reasoning given in the proof of the previous theorem, we find that the speed of the center of mass should remain the same as it was at the initial moment, i.e. null
Integrating this expression, we get
THEOREM D6. If the external forces acting on a mechanical system are balanced in a certain direction and at the initial moment the system was at rest, then the sum of the products of the masses of each of the bodies of the system and the absolute displacement of its own center of mass in the same direction is zero.
Proof. Let us choose a coordinate system in such a way that the axis X coincided with the direction in which external forces are balanced or absent ( F 1, F 2, …, F k in Fig. 3), i.e. sum of projections of external forces onto the axis X equal to zero


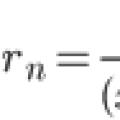 Taylor series expansion Approximate solution of the Cauchy problem for the ordinary
Taylor series expansion Approximate solution of the Cauchy problem for the ordinary What is NOT taught at school What is not taught at school ask
What is NOT taught at school What is not taught at school ask Money Thinking Formula (A
Money Thinking Formula (A