Conditional distribution law of a two-dimensional random variable. Two-dimensional random variables
Set of random variables X 1 ,X 2 ,...,X p, defined on the probability space () forms P- dimensional random variable ( X 1 ,X 2 ,...,X p). If the economic process is described using two random variables X 1 and X 2, then a two-dimensional random variable is determined ( X 1 ,X 2)or( X,Y).
Distribution function systems of two random variables ( X,Y), considered as a function of variables
is called the probability of an event occurring ![]() :
:
The distribution function values satisfy the inequality
![]()
From a geometric point of view, the distribution function F(x,y) determines the probability that a random point ( X,Y) will fall into an infinite quadrant with the vertex at point ( X,at), since the point ( X,Y) will be below and to the left of the indicated vertex (Fig. 9.1).

X,Y) in a half-strip (Fig. 9.2) or in a half-strip (Fig. 9.3) is expressed by the formulas:
respectively. Probability of hitting values X,Y) into a rectangle (Fig. 9.4) can be found using the formula:
 Fig.9.2 Fig.9.3 Fig.9.4
Fig.9.2 Fig.9.3 Fig.9.4
Discrete called a two-dimensional quantity whose components are discrete.
Law of distribution two-dimensional discrete random variable ( X,Y) is the set of all possible values ( x i, y j),
, discrete random variables X And Y and their corresponding probabilities ![]() , characterizing the probability that the component X will take the value x i and at the same time a component Y will take the value y j, and
, characterizing the probability that the component X will take the value x i and at the same time a component Y will take the value y j, and
Distribution law of a two-dimensional discrete random variable ( X,Y) are given in the form of a table. 9.1.
Table 9.1
| Ω X Ω Y | x 1 | x 2 | … | x i | … |
| y 1 | p(x 1 ,y 1) | p(x 2 ,y 1) | … | p( x i,y 1) | … |
| y 2 | p(x 1 ,y 2) | p(x 2 ,y 2) | … | p( x i,y 2) | … |
| … | … | … | … | … | … |
| y i | p(x 1 ,y i) | p(x 2 ,y i) | … | p( x i,y i) | … |
| … | … | … | … | … | … |
Continuous called a two-dimensional random variable whose components are continuous. Function R(X,at), equal to the limit of the ratio of the probability of hitting a two-dimensional random variable ( X,Y) into a rectangle with sides and to the area of this rectangle, when both sides of the rectangle tend to zero, is called probability distribution density:
Knowing the distribution density, you can find the distribution function using the formula: 
At all points where there is a second-order mixed derivative of the distribution function
, probability distribution density
can be found using the formula: 
Probability of hitting a random point ( X,at) to the area D is determined by the equality: ![]()
The probability that a random variable X took on the meaning X<х provided that the random variable Y took a fixed value Y=y, is calculated by the formula:

Likewise,

Formulas for calculating conditional probability distribution densities of components X And Y :

Set of conditional probabilities p(x 1 |y i), p(x 2 |y i), …, p(x i |y i), … meeting the condition Y=y i, is called the conditional distribution of the component X at Y=y iX,Y), Where 
Similarly, the conditional distribution of the component Y at X=x i discrete two-dimensional random variable ( X,Y) is a set of conditional probabilities that meet the condition X=x i, Where 
The initial moment of orderk+s two-dimensional random variable ( X,Y
and , i.e. ![]() .
.
If X And Y – discrete random variables, That 
If X And Y – continuous random variables, then 
Central moment order k+s two-dimensional random variable ( X,Y) is called the mathematical expectation of products ![]() And
And ![]() ,those.
,those.
If the component quantities are discrete, then

If the component quantities are continuous, then
Where R(X,y) – distribution density of a two-dimensional random variable ( X,Y).
Conditional mathematical expectationY(X)at X=x(at Y=y) is called an expression of the form:
 – for a discrete random variable Y(X);
– for a discrete random variable Y(X);
 –
for a continuous random variable Y(X).
–
for a continuous random variable Y(X).
Mathematical expectations of components X And Y two-dimensional random variable are calculated using the formulas:


Correlation moment independent random variables X And Y, included in the two-dimensional random variable ( X,Y), is called the mathematical expectation of the products of deviations of these quantities:
Correlation moment of two independent random variables XX,Y), is equal to zero.
Correlation coefficient random variables X and Y included in the two-dimensional random variable ( X,Y), is called the ratio of the correlation moment to the product of the standard deviations of these quantities:

The correlation coefficient characterizes the degree (closeness) of the linear correlation between X And Y.Random variables for which , are called uncorrelated.
The correlation coefficient satisfies the following properties:
1. The correlation coefficient does not depend on the units of measurement of random variables.
2. The absolute value of the correlation coefficient does not exceed one:
3. If then between components X And Y random variable ( X, Y) there is a linear functional relationship: ![]()
4. If then components X And Y two-dimensional random variable are uncorrelated.
5. If then components X And Y two-dimensional random variable are dependent.
Equations M(X|Y=y)=φ( at)And M(Y|X=x)=ψ( x) are called regression equations, and the lines determined by them are called regression lines.
Tasks
9.1. Two-dimensional discrete random variable (X, Y) is given by the distribution law:
Table 9.2
| Ω x Ω y | ||||
| 0,2 | 0,15 | 0,08 | 0,05 | |
| 0,1 | 0,05 | 0,05 | 0,1 | |
| 0,05 | 0,07 | 0,08 | 0,02 |
Find: a) laws of distribution of components X And Y;
b) conditional law of distribution of value Y at X =1;
c) distribution function.
Find out whether quantities are independent X And Y. Calculate probability and basic numerical characteristics M(X),M(Y),D(X),D(Y),R(X,Y), .
Solution. a) Random variables X and Y are defined on a set consisting of elementary outcomes, which has the form:
Event ( X= 1) corresponds to a set of outcomes whose first component is equal to 1: (1;0), (1;1), (1;2). These outcomes are incompatible. The probability that X will take the value x i, according to Kolmogorov’s axiom 3, is equal to:
Likewise
Therefore, the marginal distribution of the component X, can be specified in the form of a table. 9.3.
Table 9.3
b) Set of conditional probabilities R(1;0), R(1;1), R(1;2) meeting the condition X=1, is called the conditional distribution of the component Y at X=1. Probability of value values Y at X=1 we find using the formula:
Since , then, substituting the values of the corresponding probabilities, we obtain

So, the conditional distribution of the component Y at X=1 has the form:
Table 9.5
| y j | |||
| | 0,48 | 0,30 | 0,22 |

Since the conditional and unconditional distribution laws do not coincide (see Tables 9.4 and 9.5), the values X And Y dependent. This conclusion is confirmed by the fact that the equality
for any pair of possible values X And Y.
For example,
c) Distribution function F(x,y) two-dimensional random variable (X,Y) has the form:
where the summation is performed over all points (), for which the inequalities are simultaneously satisfied x i

It is more convenient to present the result in the form of Table 9.6.
Table 9.6
| X y | |||||
| 0,20 | 0,35 | 0,43 | 0,48 | ||
| 0,30 | 0,5 | 0,63 | 0,78 | ||
| 0,35 | 0,62 | 0,83 |
Let's use the formulas for the initial moments and the results of tables 9.3 and 9.4 and calculate the mathematical expectations of the components X And Y:

We calculate the variances using the second initial moment and the results of the table. 9.3 and 9.4:
To calculate covariance TO(X,Y) we use a similar formula through the initial moment:
The correlation coefficient is determined by the formula:
The required probability is defined as the probability of falling into a region on the plane defined by the corresponding inequality:
9.2. The ship transmits an “SOS” message, which can be received by two radio stations. This signal can be received by one radio station independently of the other. The probability that the signal is received by the first radio station is 0.95; the probability that the signal is received by the second radio station is 0.85. Find the distribution law of a two-dimensional random variable characterizing the reception of a signal by two radio stations. Write the distribution function.
Solution: Let X– an event consisting in the fact that the signal is received by the first radio station. Y– the event is that the signal is received by a second radio station.
Multiple meanings .
X=1 – signal received by the first radio station;
X=0 – the signal was not received by the first radio station.
Multiple meanings .
Y=l – signal received by the second radio station,
Y=0 – the signal is not received by the second radio station.
The probability that the signal is not received by either the first or second radio stations is:
Probability of signal reception by the first radio station:
Probability that the signal is received by the second radio station:
The probability that the signal is received by both the first and second radio stations is equal to: .
Then the distribution law of a two-dimensional random variable is equal to:
| y x | ||
| 0,007 | 0,142 | |
| 0,042 | 0,807 |
X,y) meaning F(X,y) is equal to the sum of the probabilities of those possible values of the random variable ( X,Y), which fall inside the specified rectangle.
Then the distribution function will look like:

9.3. Two companies produce identical products. Each, independently of the other, can decide to modernize production. The probability that the first firm made such a decision is 0.6. The probability of making such a decision by the second firm is 0.65. Write the law of distribution of a two-dimensional random variable that characterizes the decision to modernize the production of two firms. Write the distribution function.
Answer: Distribution law:
| 0,14 | 0,21 | |
| 0,26 | 0,39 |
For each fixed value of a point with coordinates ( x,y) the value is equal to the sum of the probabilities of those possible values that fall inside the specified rectangle ![]() .
.
9.4. Piston rings for car engines are made on an automatic lathe. The thickness of the ring is measured (random value X) and hole diameter (random value Y). It is known that about 5% of all piston rings are defective. Moreover, 3% of defects are caused by non-standard hole diameters, 1% - by non-standard thickness, and 1% - are rejected on both grounds. Find: joint distribution of a two-dimensional random variable ( X,Y); one-dimensional distributions of components X And Y;mathematical expectations of the components X And Y; correlation moment and correlation coefficient between components X And Y two-dimensional random variable ( X,Y).
Answer: Distribution law:
| 0,01 | 0,03 | |
| 0,01 | 0,95 |
![]() ;
; ![]() ;
; ![]() ;
; ![]() ; ; .
; ; .
9.5. Factory products are defective due to defects A is 4%, and due to a defect IN– 3.5%. Standard production is 96%. Determine what percentage of all products have both types of defects.
9.6.
Random value ( X,Y)distributed with constant density ![]() inside the square R, whose vertices have coordinates (–2;0), (0;2), (2;0), (0;–2). Determine the distribution density of the random variable ( X,Y) and conditional distribution densities R(X\at), R(at\X).
inside the square R, whose vertices have coordinates (–2;0), (0;2), (2;0), (0;–2). Determine the distribution density of the random variable ( X,Y) and conditional distribution densities R(X\at), R(at\X).
Solution. Let's build on a plane x 0y given square (Fig. 9.5) and determine the equations of the sides of the square ABCD, using the equation of a straight line passing through two given points:  Substituting the coordinates of the vertices A And IN we obtain sequentially the equation of the side AB:
Substituting the coordinates of the vertices A And IN we obtain sequentially the equation of the side AB: ![]() or
.
or
.

Similarly, we find the equation of the side Sun: ;sides CD: and sides D.A.: . : .D X , Y) is a hemisphere centered at the origin of the radius R.Find the probability distribution density.
Answer:
9.10. Given a discrete two-dimensional random variable:
| 0,25 | 0,10 | |
| 0,15 | 0,05 | |
| 0,32 | 0,13 |
Find: a) conditional distribution law X, provided that y= 10;
b) conditional distribution law Y, provided that x =10;
c) mathematical expectation, dispersion, correlation coefficient.
9.11. Continuous two-dimensional random variable ( X,Y)evenly distributed inside a right triangle with vertices ABOUT(0;0), A(0;8), IN(8,0).
Find: a) probability distribution density;
Let a two-dimensional random variable $(X,Y)$ be given.
Definition 1
The distribution law of a two-dimensional random variable $(X,Y)$ is the set of possible pairs of numbers $(x_i,\ y_j)$ (where $x_i \epsilon X,\ y_j \epsilon Y$) and their probabilities $p_(ij)$ .
Most often, the distribution law of a two-dimensional random variable is written in the form of a table (Table 1).
Figure 1. Distribution law of a two-dimensional random variable.
Let's remember now the theorem on the addition of probabilities of independent events.
Theorem 1
The probability of the sum of a finite number of independent events $(\A)_1$, $(\A)_2$, ... ,$\(\A)_n$ is calculated by the formula:
Using this formula, you can obtain the distribution laws for each component of a two-dimensional random variable, that is:
It will follow from this that the sum of all probabilities of a two-dimensional system has the following form:
Let us consider in detail (step by step) the problem associated with the concept of the distribution law of a two-dimensional random variable.
Example 1
The distribution law of a two-dimensional random variable is given by the following table:
Figure 2.
Find the laws of distribution of random variables $X,\ Y$, $X+Y$ and check in each case that the total sum of probabilities is equal to one.
- Let us first find the distribution of the random variable $X$. The random variable $X$ can take the values $x_1=2,$ $x_2=3$, $x_3=5$. To find the distribution we will use Theorem 1.
Let us first find the sum of probabilities $x_1$ as follows:

Figure 3.
Similarly, we find $P\left(x_2\right)$ and $P\left(x_3\right)$:
\ \
Figure 4.
- Let us now find the distribution of the random variable $Y$. The random variable $Y$ can take the values $x_1=1, $ $x_2=3$, $x_3=4$. To find the distribution we will use Theorem 1.
Let us first find the sum of probabilities $y_1$ as follows:

Figure 5.
Similarly, we find $P\left(y_2\right)$ and $P\left(y_3\right)$:
\ \
This means that the law of distribution of the value $X$ has the following form:
Figure 6.
Let's check the equality of the total sum of probabilities:
- It remains to find the distribution law of the random variable $X+Y$.
For convenience, let us denote it by $Z$: $Z=X+Y$.
First, let’s find what values this quantity can take. To do this, we will add the values of $X$ and $Y$ in pairs. We get the following values: 3, 4, 6, 5, 6, 8, 6, 7, 9. Now, discarding the matching values, we find that the random variable $X+Y$ can take the values $z_1=3,\ z_2=4 ,\ z_3=5,\ z_4=6,\ z_5=7,\ z_6=8,\ z_7=9.\ $
Let's first find $P(z_1)$. Since the value of $z_1$ is one, it is found as follows:

Figure 7.
All probabilities except $P(z_4)$ are found similarly:
Let us now find $P(z_4)$ as follows:

Figure 8.
This means that the law of distribution of the value $Z$ has the following form:
Figure 9.
Let's check the equality of the total sum of probabilities:
An ordered pair (X, Y) of random variables X and Y is called a two-dimensional random variable, or a random vector in two-dimensional space. A two-dimensional random variable (X,Y) is also called a system of random variables X and Y. The set of all possible values of a discrete random variable with their probabilities is called the distribution law of this random variable. A discrete two-dimensional random variable (X, Y) is considered given if its distribution law is known:
P(X=x i , Y=y j) = p ij , i=1,2...,n, j=1,2...,m
Purpose of the service. Using the service, according to a given distribution law, you can find:
- distribution series X and Y, mathematical expectation M[X], M[Y], variance D[X], D[Y];
- covariance cov(x,y), correlation coefficient r x,y, conditional distribution series X, conditional expectation M;
Instructions. Specify the dimension of the probability distribution matrix (number of rows and columns) and its type. The resulting solution is saved in a Word file.
Example No. 1. A two-dimensional discrete random variable has a distribution table:
| Y/X | 1 | 2 | 3 | 4 |
| 10 | 0 | 0,11 | 0,12 | 0,03 |
| 20 | 0 | 0,13 | 0,09 | 0,02 |
| 30 | 0,02 | 0,11 | 0,08 | 0,01 |
| 40 | 0,03 | 0,11 | 0,05 | q |
Solution. We find the value of q from the condition Σp ij = 1
Σp ij = 0.02 + 0.03 + 0.11 + … + 0.03 + 0.02 + 0.01 + q = 1
0.91+q = 1. Where does q = 0.09 come from?
Using the formula ∑P(x i,y j) = p i(j=1..n), we find the distribution series X.
M[y] = 1*0.05 + 2*0.46 + 3*0.34 + 4*0.15 = 2.59
Variance D[Y] = 1 2 *0.05 + 2 2 *0.46 + 3 2 *0.34 + 4 2 *0.15 - 2.59 2 = 0.64
Standard deviationσ(y) = sqrt(D[Y]) = sqrt(0.64) = 0.801
Covariance cov(X,Y) = M - M[X] M[Y] = 2 10 0.11 + 3 10 0.12 + 4 10 0.03 + 2 20 0.13 + 3 20 0.09 + 4 ·20·0.02 + 1·30·0.02 + 2·30·0.11 + 3·30·0.08 + 4·30·0.01 + 1·40·0.03 + 2·40·0.11 + 3·40·0.05 + 4·40 ·0.09 - 25.2 · 2.59 = -0.068
Correlation coefficient r xy = cov(x,y)/σ(x)&sigma(y) = -0.068/(11.531*0.801) = -0.00736
Example 2. Data from statistical processing of information regarding two indicators X and Y are reflected in the correlation table. Required:
- write distribution series for X and Y and calculate sample means and sample standard deviations for them;
- write conditional distribution series Y/x and calculate conditional averages Y/x;
- graphically depict the dependence of conditional averages Y/x on X values;
- calculate the sample correlation coefficient Y on X;
- write a sample forward regression equation;
- depict the data of the correlation table geometrically and construct a regression line.
The set of all possible values of a discrete random variable with their probabilities is called the distribution law of this random variable.
A discrete two-dimensional random variable (X,Y) is considered given if its distribution law is known:
P(X=x i , Y=y j) = p ij , i=1,2...,n, j=1,2..,m
| X/Y | 20 | 30 | 40 | 50 | 60 |
| 11 | 2 | 0 | 0 | 0 | 0 |
| 16 | 4 | 6 | 0 | 0 | 0 |
| 21 | 0 | 3 | 6 | 2 | 0 |
| 26 | 0 | 0 | 45 | 8 | 4 |
| 31 | 0 | 0 | 4 | 6 | 7 |
| 36 | 0 | 0 | 0 | 0 | 3 |
1. Dependence of random variables X and Y.
Find the distribution series X and Y.
Using the formula ∑P(x i,y j) = p i(j=1..n), we find the distribution series X. Expectation M[Y].
M[y] = (20*6 + 30*9 + 40*55 + 50*16 + 60*14)/100 = 42.3
Variance D[Y].
D[Y] = (20 2 *6 + 30 2 *9 + 40 2 *55 + 50 2 *16 + 60 2 *14)/100 - 42.3 2 = 99.71
Standard deviation σ(y).
Since P(X=11,Y=20) = 2≠2 6, then the random variables X and Y dependent.
2. Conditional distribution law X.
Conditional distribution law X(Y=20).
P(X=11/Y=20) = 2/6 = 0.33
P(X=16/Y=20) = 4/6 = 0.67
P(X=21/Y=20) = 0/6 = 0
P(X=26/Y=20) = 0/6 = 0
P(X=31/Y=20) = 0/6 = 0
P(X=36/Y=20) = 0/6 = 0
Conditional mathematical expectation M = 11*0.33 + 16*0.67 + 21*0 + 26*0 + 31*0 + 36*0 = 14.33
Conditional variance D = 11 2 *0.33 + 16 2 *0.67 + 21 2 *0 + 26 2 *0 + 31 2 *0 + 36 2 *0 - 14.33 2 = 5.56
Conditional distribution law X(Y=30).
P(X=11/Y=30) = 0/9 = 0
P(X=16/Y=30) = 6/9 = 0.67
P(X=21/Y=30) = 3/9 = 0.33
P(X=26/Y=30) = 0/9 = 0
P(X=31/Y=30) = 0/9 = 0
P(X=36/Y=30) = 0/9 = 0
Conditional mathematical expectation M = 11*0 + 16*0.67 + 21*0.33 + 26*0 + 31*0 + 36*0 = 17.67
Conditional variance D = 11 2 *0 + 16 2 *0.67 + 21 2 *0.33 + 26 2 *0 + 31 2 *0 + 36 2 *0 - 17.67 2 = 5.56
Conditional distribution law X(Y=40).
P(X=11/Y=40) = 0/55 = 0
P(X=16/Y=40) = 0/55 = 0
P(X=21/Y=40) = 6/55 = 0.11
P(X=26/Y=40) = 45/55 = 0.82
P(X=31/Y=40) = 4/55 = 0.0727
P(X=36/Y=40) = 0/55 = 0
Conditional mathematical expectation M = 11*0 + 16*0 + 21*0.11 + 26*0.82 + 31*0.0727 + 36*0 = 25.82
Conditional variance D = 11 2 *0 + 16 2 *0 + 21 2 *0.11 + 26 2 *0.82 + 31 2 *0.0727 + 36 2 *0 - 25.82 2 = 4.51
Conditional distribution law X(Y=50).
P(X=11/Y=50) = 0/16 = 0
P(X=16/Y=50) = 0/16 = 0
P(X=21/Y=50) = 2/16 = 0.13
P(X=26/Y=50) = 8/16 = 0.5
P(X=31/Y=50) = 6/16 = 0.38
P(X=36/Y=50) = 0/16 = 0
Conditional mathematical expectation M = 11*0 + 16*0 + 21*0.13 + 26*0.5 + 31*0.38 + 36*0 = 27.25
Conditional variance D = 11 2 *0 + 16 2 *0 + 21 2 *0.13 + 26 2 *0.5 + 31 2 *0.38 + 36 2 *0 - 27.25 2 = 10.94
Conditional distribution law X(Y=60).
P(X=11/Y=60) = 0/14 = 0
P(X=16/Y=60) = 0/14 = 0
P(X=21/Y=60) = 0/14 = 0
P(X=26/Y=60) = 4/14 = 0.29
P(X=31/Y=60) = 7/14 = 0.5
P(X=36/Y=60) = 3/14 = 0.21
Conditional mathematical expectation M = 11*0 + 16*0 + 21*0 + 26*0.29 + 31*0.5 + 36*0.21 = 30.64
Conditional variance D = 11 2 *0 + 16 2 *0 + 21 2 *0 + 26 2 *0.29 + 31 2 *0.5 + 36 2 *0.21 - 30.64 2 = 12.37
3. Conditional distribution law Y.
Conditional distribution law Y(X=11).
P(Y=20/X=11) = 2/2 = 1
P(Y=30/X=11) = 0/2 = 0
P(Y=40/X=11) = 0/2 = 0
P(Y=50/X=11) = 0/2 = 0
P(Y=60/X=11) = 0/2 = 0
Conditional mathematical expectation M = 20*1 + 30*0 + 40*0 + 50*0 + 60*0 = 20
Conditional variance D = 20 2 *1 + 30 2 *0 + 40 2 *0 + 50 2 *0 + 60 2 *0 - 20 2 = 0
Conditional distribution law Y(X=16).
P(Y=20/X=16) = 4/10 = 0.4
P(Y=30/X=16) = 6/10 = 0.6
P(Y=40/X=16) = 0/10 = 0
P(Y=50/X=16) = 0/10 = 0
P(Y=60/X=16) = 0/10 = 0
Conditional mathematical expectation M = 20*0.4 + 30*0.6 + 40*0 + 50*0 + 60*0 = 26
Conditional variance D = 20 2 *0.4 + 30 2 *0.6 + 40 2 *0 + 50 2 *0 + 60 2 *0 - 26 2 = 24
Conditional distribution law Y(X=21).
P(Y=20/X=21) = 0/11 = 0
P(Y=30/X=21) = 3/11 = 0.27
P(Y=40/X=21) = 6/11 = 0.55
P(Y=50/X=21) = 2/11 = 0.18
P(Y=60/X=21) = 0/11 = 0
Conditional mathematical expectation M = 20*0 + 30*0.27 + 40*0.55 + 50*0.18 + 60*0 = 39.09
Conditional variance D = 20 2 *0 + 30 2 *0.27 + 40 2 *0.55 + 50 2 *0.18 + 60 2 *0 - 39.09 2 = 44.63
Conditional distribution law Y(X=26).
P(Y=20/X=26) = 0/57 = 0
P(Y=30/X=26) = 0/57 = 0
P(Y=40/X=26) = 45/57 = 0.79
P(Y=50/X=26) = 8/57 = 0.14
P(Y=60/X=26) = 4/57 = 0.0702
Conditional mathematical expectation M = 20*0 + 30*0 + 40*0.79 + 50*0.14 + 60*0.0702 = 42.81
Conditional variance D = 20 2 *0 + 30 2 *0 + 40 2 *0.79 + 50 2 *0.14 + 60 2 *0.0702 - 42.81 2 = 34.23
Conditional distribution law Y(X=31).
P(Y=20/X=31) = 0/17 = 0
P(Y=30/X=31) = 0/17 = 0
P(Y=40/X=31) = 4/17 = 0.24
P(Y=50/X=31) = 6/17 = 0.35
P(Y=60/X=31) = 7/17 = 0.41
Conditional mathematical expectation M = 20*0 + 30*0 + 40*0.24 + 50*0.35 + 60*0.41 = 51.76
Conditional variance D = 20 2 *0 + 30 2 *0 + 40 2 *0.24 + 50 2 *0.35 + 60 2 *0.41 - 51.76 2 = 61.59
Conditional distribution law Y(X=36).
P(Y=20/X=36) = 0/3 = 0
P(Y=30/X=36) = 0/3 = 0
P(Y=40/X=36) = 0/3 = 0
P(Y=50/X=36) = 0/3 = 0
P(Y=60/X=36) = 3/3 = 1
Conditional mathematical expectation M = 20*0 + 30*0 + 40*0 + 50*0 + 60*1 = 60
Conditional variance D = 20 2 *0 + 30 2 *0 + 40 2 *0 + 50 2 *0 + 60 2 *1 - 60 2 = 0
Covariance.
cov(X,Y) = M - M[X]·M[Y]
cov(X,Y) = (20 11 2 + 20 16 4 + 30 16 6 + 30 21 3 + 40 21 6 + 50 21 2 + 40 26 45 + 50 26 8 + 60 26 4 + 40 31 4 + 50 31 6 + 60 31 7 + 60 36 3)/100 - 25.3 42.3 = 38.11
If random variables are independent, then their covariance is zero. In our case, cov(X,Y) ≠ 0.
Correlation coefficient.
The linear regression equation from y to x is:
The linear regression equation from x to y is:
Let's find the necessary numerical characteristics.
Sample averages:
x = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 42.3
y = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 25.3
Variances:
σ 2 x = (20 2 (2 + 4) + 30 2 (6 + 3) + 40 2 (6 + 45 + 4) + 50 2 (2 + 8 + 6) + 60 2 (4 + 7 + 3) )/100 - 42.3 2 = 99.71
σ 2 y = (11 2 (2) + 16 2 (4 + 6) + 21 2 (3 + 6 + 2) + 26 2 (45 + 8 + 4) + 31 2 (4 + 6 + 7) + 36 2 (3))/100 - 25.3 2 = 24.01
Where do we get standard deviations from:
σ x = 9.99 and σ y = 4.9
and covariance:
Cov(x,y) = (20 11 2 + 20 16 4 + 30 16 6 + 30 21 3 + 40 21 6 + 50 21 2 + 40 26 45 + 50 26 8 + 60 26 4 + 40 31 4 + 50 31 6 + 60 31 7 + 60 36 3)/100 - 42.3 25.3 = 38.11
Let's determine the correlation coefficient:
Let us write down the equations of the regression lines y(x):
and calculating, we get:
y x = 0.38 x + 9.14
Let us write down the equations of the regression lines x(y):
and calculating, we get:
x y = 1.59 y + 2.15
If we plot the points determined by the table and the regression lines, we will see that both lines pass through the point with coordinates (42.3; 25.3) and the points are located close to the regression lines.
Significance of the correlation coefficient.

Using the Student's table with significance level α=0.05 and degrees of freedom k=100-m-1 = 98, we find t crit:
t crit (n-m-1;α/2) = (98;0.025) = 1.984
where m = 1 is the number of explanatory variables.
If t observed > t critical, then the resulting value of the correlation coefficient is considered significant (the null hypothesis stating that the correlation coefficient is equal to zero is rejected).
Since t obs > t crit, we reject the hypothesis that the correlation coefficient is equal to 0. In other words, the correlation coefficient is statistically significant.
Exercise. The number of hits of pairs of values of random variables X and Y in the corresponding intervals is given in the table. Using these data, find the sample correlation coefficient and sample equations of straight regression lines of Y on X and X on Y.
Solution
Example. The probability distribution of a two-dimensional random variable (X, Y) is given by a table. Find the laws of distribution of the component quantities X, Y and the correlation coefficient p(X, Y).
Download solution
Exercise. A two-dimensional discrete quantity (X, Y) is given by a distribution law. Find the laws of distribution of components X and Y, covariance and correlation coefficient.
An ordered pair (X, Y) of random variables X and Y is called a two-dimensional random variable, or a random vector in two-dimensional space. A two-dimensional random variable (X,Y) is also called a system of random variables X and Y. The set of all possible values of a discrete random variable with their probabilities is called the distribution law of this random variable. A discrete two-dimensional random variable (X, Y) is considered given if its distribution law is known:
P(X=x i , Y=y j) = p ij , i=1,2...,n, j=1,2...,m
Purpose of the service. Using the service, according to a given distribution law, you can find:
- distribution series X and Y, mathematical expectation M[X], M[Y], variance D[X], D[Y];
- covariance cov(x,y), correlation coefficient r x,y, conditional distribution series X, conditional expectation M;
Instructions. Specify the dimension of the probability distribution matrix (number of rows and columns) and its type. The resulting solution is saved in a Word file.
Example No. 1. A two-dimensional discrete random variable has a distribution table:
| Y/X | 1 | 2 | 3 | 4 |
| 10 | 0 | 0,11 | 0,12 | 0,03 |
| 20 | 0 | 0,13 | 0,09 | 0,02 |
| 30 | 0,02 | 0,11 | 0,08 | 0,01 |
| 40 | 0,03 | 0,11 | 0,05 | q |
Solution. We find the value of q from the condition Σp ij = 1
Σp ij = 0.02 + 0.03 + 0.11 + … + 0.03 + 0.02 + 0.01 + q = 1
0.91+q = 1. Where does q = 0.09 come from?
Using the formula ∑P(x i,y j) = p i(j=1..n), we find the distribution series X.
M[y] = 1*0.05 + 2*0.46 + 3*0.34 + 4*0.15 = 2.59
Variance D[Y] = 1 2 *0.05 + 2 2 *0.46 + 3 2 *0.34 + 4 2 *0.15 - 2.59 2 = 0.64
Standard deviationσ(y) = sqrt(D[Y]) = sqrt(0.64) = 0.801
Covariance cov(X,Y) = M - M[X] M[Y] = 2 10 0.11 + 3 10 0.12 + 4 10 0.03 + 2 20 0.13 + 3 20 0.09 + 4 ·20·0.02 + 1·30·0.02 + 2·30·0.11 + 3·30·0.08 + 4·30·0.01 + 1·40·0.03 + 2·40·0.11 + 3·40·0.05 + 4·40 ·0.09 - 25.2 · 2.59 = -0.068
Correlation coefficient r xy = cov(x,y)/σ(x)&sigma(y) = -0.068/(11.531*0.801) = -0.00736
Example 2. Data from statistical processing of information regarding two indicators X and Y are reflected in the correlation table. Required:
- write distribution series for X and Y and calculate sample means and sample standard deviations for them;
- write conditional distribution series Y/x and calculate conditional averages Y/x;
- graphically depict the dependence of conditional averages Y/x on X values;
- calculate the sample correlation coefficient Y on X;
- write a sample forward regression equation;
- depict the data of the correlation table geometrically and construct a regression line.
The set of all possible values of a discrete random variable with their probabilities is called the distribution law of this random variable.
A discrete two-dimensional random variable (X,Y) is considered given if its distribution law is known:
P(X=x i , Y=y j) = p ij , i=1,2...,n, j=1,2..,m
| X/Y | 20 | 30 | 40 | 50 | 60 |
| 11 | 2 | 0 | 0 | 0 | 0 |
| 16 | 4 | 6 | 0 | 0 | 0 |
| 21 | 0 | 3 | 6 | 2 | 0 |
| 26 | 0 | 0 | 45 | 8 | 4 |
| 31 | 0 | 0 | 4 | 6 | 7 |
| 36 | 0 | 0 | 0 | 0 | 3 |
1. Dependence of random variables X and Y.
Find the distribution series X and Y.
Using the formula ∑P(x i,y j) = p i(j=1..n), we find the distribution series X. Expectation M[Y].
M[y] = (20*6 + 30*9 + 40*55 + 50*16 + 60*14)/100 = 42.3
Variance D[Y].
D[Y] = (20 2 *6 + 30 2 *9 + 40 2 *55 + 50 2 *16 + 60 2 *14)/100 - 42.3 2 = 99.71
Standard deviation σ(y).
Since P(X=11,Y=20) = 2≠2 6, then the random variables X and Y dependent.
2. Conditional distribution law X.
Conditional distribution law X(Y=20).
P(X=11/Y=20) = 2/6 = 0.33
P(X=16/Y=20) = 4/6 = 0.67
P(X=21/Y=20) = 0/6 = 0
P(X=26/Y=20) = 0/6 = 0
P(X=31/Y=20) = 0/6 = 0
P(X=36/Y=20) = 0/6 = 0
Conditional mathematical expectation M = 11*0.33 + 16*0.67 + 21*0 + 26*0 + 31*0 + 36*0 = 14.33
Conditional variance D = 11 2 *0.33 + 16 2 *0.67 + 21 2 *0 + 26 2 *0 + 31 2 *0 + 36 2 *0 - 14.33 2 = 5.56
Conditional distribution law X(Y=30).
P(X=11/Y=30) = 0/9 = 0
P(X=16/Y=30) = 6/9 = 0.67
P(X=21/Y=30) = 3/9 = 0.33
P(X=26/Y=30) = 0/9 = 0
P(X=31/Y=30) = 0/9 = 0
P(X=36/Y=30) = 0/9 = 0
Conditional mathematical expectation M = 11*0 + 16*0.67 + 21*0.33 + 26*0 + 31*0 + 36*0 = 17.67
Conditional variance D = 11 2 *0 + 16 2 *0.67 + 21 2 *0.33 + 26 2 *0 + 31 2 *0 + 36 2 *0 - 17.67 2 = 5.56
Conditional distribution law X(Y=40).
P(X=11/Y=40) = 0/55 = 0
P(X=16/Y=40) = 0/55 = 0
P(X=21/Y=40) = 6/55 = 0.11
P(X=26/Y=40) = 45/55 = 0.82
P(X=31/Y=40) = 4/55 = 0.0727
P(X=36/Y=40) = 0/55 = 0
Conditional mathematical expectation M = 11*0 + 16*0 + 21*0.11 + 26*0.82 + 31*0.0727 + 36*0 = 25.82
Conditional variance D = 11 2 *0 + 16 2 *0 + 21 2 *0.11 + 26 2 *0.82 + 31 2 *0.0727 + 36 2 *0 - 25.82 2 = 4.51
Conditional distribution law X(Y=50).
P(X=11/Y=50) = 0/16 = 0
P(X=16/Y=50) = 0/16 = 0
P(X=21/Y=50) = 2/16 = 0.13
P(X=26/Y=50) = 8/16 = 0.5
P(X=31/Y=50) = 6/16 = 0.38
P(X=36/Y=50) = 0/16 = 0
Conditional mathematical expectation M = 11*0 + 16*0 + 21*0.13 + 26*0.5 + 31*0.38 + 36*0 = 27.25
Conditional variance D = 11 2 *0 + 16 2 *0 + 21 2 *0.13 + 26 2 *0.5 + 31 2 *0.38 + 36 2 *0 - 27.25 2 = 10.94
Conditional distribution law X(Y=60).
P(X=11/Y=60) = 0/14 = 0
P(X=16/Y=60) = 0/14 = 0
P(X=21/Y=60) = 0/14 = 0
P(X=26/Y=60) = 4/14 = 0.29
P(X=31/Y=60) = 7/14 = 0.5
P(X=36/Y=60) = 3/14 = 0.21
Conditional mathematical expectation M = 11*0 + 16*0 + 21*0 + 26*0.29 + 31*0.5 + 36*0.21 = 30.64
Conditional variance D = 11 2 *0 + 16 2 *0 + 21 2 *0 + 26 2 *0.29 + 31 2 *0.5 + 36 2 *0.21 - 30.64 2 = 12.37
3. Conditional distribution law Y.
Conditional distribution law Y(X=11).
P(Y=20/X=11) = 2/2 = 1
P(Y=30/X=11) = 0/2 = 0
P(Y=40/X=11) = 0/2 = 0
P(Y=50/X=11) = 0/2 = 0
P(Y=60/X=11) = 0/2 = 0
Conditional mathematical expectation M = 20*1 + 30*0 + 40*0 + 50*0 + 60*0 = 20
Conditional variance D = 20 2 *1 + 30 2 *0 + 40 2 *0 + 50 2 *0 + 60 2 *0 - 20 2 = 0
Conditional distribution law Y(X=16).
P(Y=20/X=16) = 4/10 = 0.4
P(Y=30/X=16) = 6/10 = 0.6
P(Y=40/X=16) = 0/10 = 0
P(Y=50/X=16) = 0/10 = 0
P(Y=60/X=16) = 0/10 = 0
Conditional mathematical expectation M = 20*0.4 + 30*0.6 + 40*0 + 50*0 + 60*0 = 26
Conditional variance D = 20 2 *0.4 + 30 2 *0.6 + 40 2 *0 + 50 2 *0 + 60 2 *0 - 26 2 = 24
Conditional distribution law Y(X=21).
P(Y=20/X=21) = 0/11 = 0
P(Y=30/X=21) = 3/11 = 0.27
P(Y=40/X=21) = 6/11 = 0.55
P(Y=50/X=21) = 2/11 = 0.18
P(Y=60/X=21) = 0/11 = 0
Conditional mathematical expectation M = 20*0 + 30*0.27 + 40*0.55 + 50*0.18 + 60*0 = 39.09
Conditional variance D = 20 2 *0 + 30 2 *0.27 + 40 2 *0.55 + 50 2 *0.18 + 60 2 *0 - 39.09 2 = 44.63
Conditional distribution law Y(X=26).
P(Y=20/X=26) = 0/57 = 0
P(Y=30/X=26) = 0/57 = 0
P(Y=40/X=26) = 45/57 = 0.79
P(Y=50/X=26) = 8/57 = 0.14
P(Y=60/X=26) = 4/57 = 0.0702
Conditional mathematical expectation M = 20*0 + 30*0 + 40*0.79 + 50*0.14 + 60*0.0702 = 42.81
Conditional variance D = 20 2 *0 + 30 2 *0 + 40 2 *0.79 + 50 2 *0.14 + 60 2 *0.0702 - 42.81 2 = 34.23
Conditional distribution law Y(X=31).
P(Y=20/X=31) = 0/17 = 0
P(Y=30/X=31) = 0/17 = 0
P(Y=40/X=31) = 4/17 = 0.24
P(Y=50/X=31) = 6/17 = 0.35
P(Y=60/X=31) = 7/17 = 0.41
Conditional mathematical expectation M = 20*0 + 30*0 + 40*0.24 + 50*0.35 + 60*0.41 = 51.76
Conditional variance D = 20 2 *0 + 30 2 *0 + 40 2 *0.24 + 50 2 *0.35 + 60 2 *0.41 - 51.76 2 = 61.59
Conditional distribution law Y(X=36).
P(Y=20/X=36) = 0/3 = 0
P(Y=30/X=36) = 0/3 = 0
P(Y=40/X=36) = 0/3 = 0
P(Y=50/X=36) = 0/3 = 0
P(Y=60/X=36) = 3/3 = 1
Conditional mathematical expectation M = 20*0 + 30*0 + 40*0 + 50*0 + 60*1 = 60
Conditional variance D = 20 2 *0 + 30 2 *0 + 40 2 *0 + 50 2 *0 + 60 2 *1 - 60 2 = 0
Covariance.
cov(X,Y) = M - M[X]·M[Y]
cov(X,Y) = (20 11 2 + 20 16 4 + 30 16 6 + 30 21 3 + 40 21 6 + 50 21 2 + 40 26 45 + 50 26 8 + 60 26 4 + 40 31 4 + 50 31 6 + 60 31 7 + 60 36 3)/100 - 25.3 42.3 = 38.11
If random variables are independent, then their covariance is zero. In our case, cov(X,Y) ≠ 0.
Correlation coefficient.
The linear regression equation from y to x is:
The linear regression equation from x to y is:
Let's find the necessary numerical characteristics.
Sample averages:
x = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 42.3
y = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 25.3
Variances:
σ 2 x = (20 2 (2 + 4) + 30 2 (6 + 3) + 40 2 (6 + 45 + 4) + 50 2 (2 + 8 + 6) + 60 2 (4 + 7 + 3) )/100 - 42.3 2 = 99.71
σ 2 y = (11 2 (2) + 16 2 (4 + 6) + 21 2 (3 + 6 + 2) + 26 2 (45 + 8 + 4) + 31 2 (4 + 6 + 7) + 36 2 (3))/100 - 25.3 2 = 24.01
Where do we get standard deviations from:
σ x = 9.99 and σ y = 4.9
and covariance:
Cov(x,y) = (20 11 2 + 20 16 4 + 30 16 6 + 30 21 3 + 40 21 6 + 50 21 2 + 40 26 45 + 50 26 8 + 60 26 4 + 40 31 4 + 50 31 6 + 60 31 7 + 60 36 3)/100 - 42.3 25.3 = 38.11
Let's determine the correlation coefficient:
Let us write down the equations of the regression lines y(x):
and calculating, we get:
y x = 0.38 x + 9.14
Let us write down the equations of the regression lines x(y):
and calculating, we get:
x y = 1.59 y + 2.15
If we plot the points determined by the table and the regression lines, we will see that both lines pass through the point with coordinates (42.3; 25.3) and the points are located close to the regression lines.
Significance of the correlation coefficient.

Using the Student's table with significance level α=0.05 and degrees of freedom k=100-m-1 = 98, we find t crit:
t crit (n-m-1;α/2) = (98;0.025) = 1.984
where m = 1 is the number of explanatory variables.
If t observed > t critical, then the resulting value of the correlation coefficient is considered significant (the null hypothesis stating that the correlation coefficient is equal to zero is rejected).
Since t obs > t crit, we reject the hypothesis that the correlation coefficient is equal to 0. In other words, the correlation coefficient is statistically significant.
Exercise. The number of hits of pairs of values of random variables X and Y in the corresponding intervals is given in the table. Using these data, find the sample correlation coefficient and sample equations of straight regression lines of Y on X and X on Y.
Solution
Example. The probability distribution of a two-dimensional random variable (X, Y) is given by a table. Find the laws of distribution of the component quantities X, Y and the correlation coefficient p(X, Y).
Download solution
Exercise. A two-dimensional discrete quantity (X, Y) is given by a distribution law. Find the laws of distribution of components X and Y, covariance and correlation coefficient.
two-dimensional discrete distribution random
Often the result of an experiment is described by several random variables: . For example, the weather in this place at a certain time of day can be characterized by the following random variables: X 1 - temperature, X 2 - pressure, X 3 - air humidity, X 4 - wind speed.
In this case, we speak of a multidimensional random variable or a system of random variables.
Consider a two-dimensional random variable whose possible values are pairs of numbers. Geometrically, a two-dimensional random variable can be interpreted as a random point on a plane.
If the components X And Y are discrete random variables, then is a discrete two-dimensional random variable, and if X And Y are continuous, then is a continuous two-dimensional random variable.
The law of probability distribution of a two-dimensional random variable is the correspondence between possible values and their probabilities.
The distribution law of a two-dimensional discrete random variable can be specified in the form of a table with a double input (see Table 6.1), where is the probability that the component X took on the meaning x i, and the component Y- meaning y j .
Table 6.1.1.
|
y 1 |
y 2 |
y j |
y m |
|||
|
x 1 |
p 11 |
p 12 |
p 1j |
p 1m |
||
|
x 2 |
p 21 |
p 22 |
p 2j |
p 2m |
||
|
x i |
p i1 |
p i2 |
p ij |
p im |
||
|
x n |
p n1 |
p n2 |
p nj |
p nm |
Since the events constitute a complete group of pairwise incompatible events, the sum of the probabilities is equal to 1, i.e.
From Table 6.1 you can find the laws of distribution of one-dimensional components X And Y.
Example 6.1.1 . Find the laws of distribution of components X And Y, if the distribution of a two-dimensional random variable is given in the form of table 6.1.2.
Table 6.1.2.
If we fix the value of one of the arguments, for example, then the resulting distribution of the value X called conditional distribution. The conditional distribution is defined similarly Y.
Example 6.1.2 . According to the distribution of a two-dimensional random variable given in Table. 6.1.2, find: a) the conditional distribution law of the component X given that; b) conditional distribution law Y provided that.
Solution. Conditional probabilities components X And Y calculated using formulas


Conditional distribution law X provided it has the form
Control: .
The distribution law of a two-dimensional random variable can be specified in the form distribution functions, which determines for each pair of numbers the probability that X will take a value less than X, and wherein Y will take a value less than y:
Geometrically, the function means the probability of a random point falling into an infinite square with its vertex at the point (Fig. 6.1.1).

Let's note the properties.
- 1. The range of values of the function is , i.e. .
- 2. Function - a non-decreasing function for each argument.
- 3. There are limiting relations:
When the distribution function of the system becomes equal to the distribution function of the component X, i.e. .
Likewise, .
Knowing this, you can find the probability of a random point falling within the rectangle ABCD.

Namely,
Example 6.1.3. A two-dimensional discrete random variable is specified by a distribution table
Find the distribution function.
Solution. Value in case of discrete components X And Y is found by summing all probabilities with indices i And j, for which, . Then, if and, then (the events and are impossible). Similarly we get:
if and, then;
if and, then;
if and, then;
if and, then;
if and, then;
if and, then;
if and, then;
if and, then;
if and, then.
Let us present the results obtained in the form of a table (6.1.3) of values:
For two-dimensional continuous random variable, the concept of probability density is introduced
Geometric probability density is a distribution surface in space

The two-dimensional probability density has the following properties:
3. The distribution function can be expressed through the formula
4. The probability of a continuous random variable falling into the region is equal to
5. In accordance with property (4) of the function, the following formulas hold:
Example 6.1.4. The distribution function of a two-dimensional random variable is given
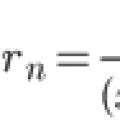 Taylor series expansion Approximate solution of the Cauchy problem for the ordinary
Taylor series expansion Approximate solution of the Cauchy problem for the ordinary What is NOT taught at school What is not taught at school ask
What is NOT taught at school What is not taught at school ask Money Thinking Formula (A
Money Thinking Formula (A