Solving exponential equations that reduce to quadratic. Solving exponential equations
1º. Exponential equations are called equations containing a variable in an exponent.
Solving exponential equations is based on the property of powers: two powers with the same base are equal if and only if their exponents are equal.
2º. Basic methods for solving exponential equations:
1) the simplest equation has a solution;
2) an equation of the form logarithmic to the base a reduce to form;
3) an equation of the form is equivalent to the equation ;
4) equation of the form ![]() is equivalent to the equation.
is equivalent to the equation.
5) an equation of the form is reduced through substitution to an equation, and then a set of simple exponential equations is solved;
6) equation with reciprocals ![]() by substitution they reduce to an equation, and then solve a set of equations;
by substitution they reduce to an equation, and then solve a set of equations;
7) equations homogeneous with respect to a g(x) And b g(x) given that ![]() kind
kind ![]() through replacement they are reduced to an equation, and then a set of equations is solved.
through replacement they are reduced to an equation, and then a set of equations is solved.
Classification of exponential equations.
1. Equations solved by going to one base.
Example 18. Solve the equation ![]() .
.
Solution: Let's take advantage of the fact that all bases of powers are powers of the number 5: .
2. Equations solved by passing to one exponent.
These equations are solved by transforming the original equation to the form ![]() , which is reduced to its simplest using the property of proportion.
, which is reduced to its simplest using the property of proportion.
Example 19. Solve the equation:
3. Equations solved by taking the common factor out of brackets.
If each exponent in an equation differs from the other by a certain number, then the equations are solved by putting the exponent with the smallest exponent out of brackets.
Example 20. Solve the equation.
Solution: Let’s take the degree with the smallest exponent out of brackets on the left side of the equation:
Example 21. Solve the equation ![]()
Solution: Let's group separately on the left side of the equation the terms containing powers with base 4, on the right side - with base 3, then put the powers with the smallest exponent out of brackets:
4. Equations that reduce to quadratic (or cubic) equations.
The following equations are reduced to a quadratic equation for the new variable y:
a) the type of substitution, in this case;
b) the type of substitution , and .
Example 22. Solve the equation ![]() .
.
Solution: Let's make a change of variable and solve the quadratic equation:
 .
.
Answer: 0; 1.
5. Equations that are homogeneous with respect to exponential functions.
An equation of the form is a homogeneous equation of the second degree with respect to the unknowns a x And b x. Such equations are reduced by first dividing both sides by and then substituting them into quadratic equations.
Example 23. Solve the equation.
Solution: Divide both sides of the equation by:
Putting , we get a quadratic equation with roots .
Now the problem comes down to solving a set of equations ![]() . From the first equation we find that . The second equation has no roots, since for any value x.
. From the first equation we find that . The second equation has no roots, since for any value x.
Answer: -1/2.
6. Rational equations with respect to exponential functions.
Example 24. Solve the equation.
Solution: Divide the numerator and denominator of the fraction by 3 x and instead of two we get one exponential function:

7. Equations of the form ![]() .
.
Such equations with a set of admissible values (APV), determined by the condition, by taking the logarithm of both sides of the equation are reduced to an equivalent equation, which in turn are equivalent to a set of two equations or.
Example 25. Solve the equation: .
 .
.
Didactic material.
Solve the equations:
1. ; 2. ; 3.  ;
;
4.  ; 5. ; 6. ;
; 5. ; 6. ;
9. ![]() ; 10.
; 10. ![]() ; 11.
; 11. ![]() ;
;
14. ![]() ; 15. ;
; 15. ;
16. ![]() ; 17.
; 17. ![]() ;
;
18. ; 19. ![]() ;
;
20. ; 21. ![]() ;
;
22. ![]() ; 23.
; 23. ![]() ;
;
24. ![]() ; 25.
; 25. ![]() .
.
26. Find the product of the roots of the equation ![]() .
.
27. Find the sum of the roots of the equation ![]() .
.
Find the meaning of the expression:
28. , where x 0- root of the equation ;
29. , where x 0– whole root of the equation ![]() .
.
Solve the equation:
31. ![]() ; 32. .
; 32. .
Answers: 10; 2. -2/9; 3. 1/36; 4. 0, 0.5; 50; 6.0; 7. -2; 8.2; 9. 1, 3; 10. 8; 11.5; 12.1; 13. ¼; 14.2; 15. -2, -1; 16. -2, 1; 17.0; 18.1; 19.0; 20. -1, 0; 21. -2, 2; 22. -2, 2; 23.4; 24. -1, 2; 25. -2, -1, 3; 26. -0.3; 27.3; 28.11; 29.54; 30. -1, 0, 2, 3; 31. ; 32. .
Topic No. 8.
Exponential inequalities.
1º. An inequality containing a variable in the exponent is called exponential inequality.
2º. The solution to exponential inequalities of the form is based on the following statements:
if , then the inequality is equivalent to ;
if , then the inequality is equivalent to .
When solving exponential inequalities, the same techniques are used as when solving exponential equations.
Example 26. Solve inequality ![]() (method of transition to one base).
(method of transition to one base).
Solution: Because ![]() , then the given inequality can be written as:
, then the given inequality can be written as: ![]() . Since , then this inequality is equivalent to the inequality
. Since , then this inequality is equivalent to the inequality ![]() .
.
Solving the last inequality, we get .
Example 27. Solve the inequality: ( by taking the common factor out of brackets).
Solution: Let's take out of brackets on the left side of the inequality , on the right side of the inequality and divide both sides of the inequality by (-2), changing the sign of the inequality to the opposite:
Since , then when moving to inequality of indicators, the sign of inequality again changes to the opposite. We get. Thus, the set of all solutions to this inequality is the interval.
Example 28. Solve inequality ( by introducing a new variable).
Solution: Let . Then this inequality will take the form: ![]() or
or ![]() , whose solution is the interval .
, whose solution is the interval .
From here. Since the function increases, then .
Didactic material.
Specify the set of solutions to the inequality:
1. ; 2. ; 3. ;
6. At what values x Do the points on the function graph lie below the straight line?
7. At what values x Do the points on the graph of the function lie at least as low as the straight line?
Solve the inequality:
8. ![]() ; 9.
; 9. ![]() ; 10. ;
; 10. ;
13. Specify the largest integer solution to the inequality ![]() .
.
14. Find the product of the largest integer and the smallest integer solutions to the inequality ![]() .
.
Solve the inequality:
15. ; 16. ![]() ; 17.
; 17. ![]() ;
;
18. ![]() ; 19. ; 20. ;
; 19. ; 20. ;
21. ![]() ; 22.
; 22. ![]() ; 23.
; 23. ![]() ;
;
24. ![]() ; 25.
; 25.  ; 26.
; 26. ![]() .
.
Find the domain of the function:
27.  ; 28.
; 28. ![]() .
.
29. Find the set of argument values for which the values of each of the functions are greater than 3:
![]() And
And  .
.
Answers: 11.3; 12.3; 13. -3; 14.1; 15. (0; 0.5); 16. ; 17. (-1; 0)U(3; 4); 18. [-2; 2]; 19. (0; +∞); 20. (0; 1); 21. (3; +∞); 22. (-∞; 0)U(0.5; +∞); 23. (0; 1); 24. (-1; 1); 25. (0; 2]; 26. (3; 3.5)U (4; +∞); 27. (-∞; 3)U(5); 28.
Some of them may seem more complex to you, while others, on the contrary, are too simple. But they all have one important feature in common: their notation contains the exponential function $f\left(x \right)=((a)^(x))$. Thus, let's introduce the definition:
An exponential equation is any equation containing an exponential function, i.e. expression of the form $((a)^(x))$. In addition to the indicated function, such equations can contain any other algebraic constructions - polynomials, roots, trigonometry, logarithms, etc.
OK then. We've sorted out the definition. Now the question is: how to solve all this crap? The answer is both simple and complex.
Let's start with the good news: from my experience of teaching many students, I can say that most of them find exponential equations much easier than the same logarithms, and even more so trigonometry.
But there is bad news: sometimes the writers of problems for all kinds of textbooks and exams are struck by “inspiration”, and their drug-inflamed brain begins to produce such brutal equations that solving them becomes problematic not only for students - even many teachers get stuck on such problems.
However, let's not talk about sad things. And let's return to those three equations that were given at the very beginning of the story. Let's try to solve each of them.
First equation: $((2)^(x))=4$. Well, to what power must you raise the number 2 to get the number 4? Probably the second? After all, $((2)^(2))=2\cdot 2=4$ - and we got the correct numerical equality, i.e. indeed $x=2$. Well, thanks, Cap, but this equation was so simple that even my cat could solve it. :)
Let's look at the following equation:
\[((5)^(2x-3))=\frac(1)(25)\]
But here it’s a little more complicated. Many students know that $((5)^(2))=25$ is the multiplication table. Some also suspect that $((5)^(-1))=\frac(1)(5)$ is essentially the definition of negative powers (similar to the formula $((a)^(-n))= \frac(1)(((a)^(n)))$).
Finally, only a select few realize that these facts can be combined and yield the following result:
\[\frac(1)(25)=\frac(1)(((5)^(2)))=((5)^(-2))\]
Thus, our original equation will be rewritten as follows:
\[((5)^(2x-3))=\frac(1)(25)\Rightarrow ((5)^(2x-3))=((5)^(-2))\]
But this is already completely solvable! On the left in the equation there is an exponential function, on the right in the equation there is an exponential function, there is nothing else anywhere except them. Therefore, we can “discard” the bases and stupidly equate the indicators:
We have obtained the simplest linear equation that any student can solve in just a couple of lines. Okay, in four lines:
\[\begin(align)& 2x-3=-2 \\& 2x=3-2 \\& 2x=1 \\& x=\frac(1)(2) \\\end(align)\]
If you don’t understand what happened in the last four lines, be sure to return to the topic “linear equations” and repeat it. Because without a clear understanding of this topic, it is too early for you to take on exponential equations.
\[((9)^(x))=-3\]
So how can we solve this? First thought: $9=3\cdot 3=((3)^(2))$, so the original equation can be rewritten as follows:
\[((\left(((3)^(2)) \right))^(x))=-3\]
Then we remember that when raising a power to a power, the exponents are multiplied:
\[((\left(((3)^(2)) \right))^(x))=((3)^(2x))\Rightarrow ((3)^(2x))=-(( 3)^(1))\]
\[\begin(align)& 2x=-1 \\& x=-\frac(1)(2) \\\end(align)\]
And for such a decision we will receive a honestly deserved two. For, with the equanimity of a Pokemon, we sent the minus sign in front of the three to the power of this very three. But you can’t do that. And that's why. Take a look at the different powers of three:
\[\begin(matrix) ((3)^(1))=3& ((3)^(-1))=\frac(1)(3)& ((3)^(\frac(1)( 2)))=\sqrt(3) \\ ((3)^(2))=9& ((3)^(-2))=\frac(1)(9)& ((3)^(\ frac(1)(3)))=\sqrt(3) \\ ((3)^(3))=27& ((3)^(-3))=\frac(1)(27)& (( 3)^(-\frac(1)(2)))=\frac(1)(\sqrt(3)) \\\end(matrix)\]
When compiling this tablet, I did not pervert anything: I looked at positive powers, and negative ones, and even fractional ones... well, where is at least one negative number here? He's gone! And it cannot be, because the exponential function $y=((a)^(x))$, firstly, always takes only positive values (no matter how much one is multiplied or divided by two, it will still be a positive number), and secondly, the base of such a function - the number $a$ - is by definition a positive number!
Well, how then to solve the equation $((9)^(x))=-3$? But no way: there are no roots. And in this sense, exponential equations are very similar to quadratic equations - there may also be no roots. But if in quadratic equations the number of roots is determined by the discriminant (positive discriminant - 2 roots, negative - no roots), then in exponential equations everything depends on what is to the right of the equal sign.
Thus, we formulate the key conclusion: the simplest exponential equation of the form $((a)^(x))=b$ has a root if and only if $b \gt 0$. Knowing this simple fact, you can easily determine whether the equation proposed to you has roots or not. Those. Is it worth solving it at all or immediately writing down that there are no roots.
This knowledge will help us many times when we have to solve more complex problems. For now, enough of the lyrics - it’s time to study the basic algorithm for solving exponential equations.
How to Solve Exponential Equations
So, let's formulate the problem. It is necessary to solve the exponential equation:
\[((a)^(x))=b,\quad a,b \gt 0\]
According to the “naive” algorithm that we used earlier, it is necessary to represent the number $b$ as a power of the number $a$:
In addition, if instead of the variable $x$ there is any expression, we will get a new equation that can already be solved. For example:
\[\begin(align)& ((2)^(x))=8\Rightarrow ((2)^(x))=((2)^(3))\Rightarrow x=3; \\& ((3)^(-x))=81\Rightarrow ((3)^(-x))=((3)^(4))\Rightarrow -x=4\Rightarrow x=-4; \\& ((5)^(2x))=125\Rightarrow ((5)^(2x))=((5)^(3))\Rightarrow 2x=3\Rightarrow x=\frac(3)( 2). \\\end(align)\]
And oddly enough, this scheme works in about 90% of cases. What then about the remaining 10%? The remaining 10% are slightly “schizophrenic” exponential equations of the form:
\[((2)^(x))=3;\quad ((5)^(x))=15;\quad ((4)^(2x))=11\]
Well, to what power do you need to raise 2 to get 3? First? But no: $((2)^(1))=2$ is not enough. Second? No either: $((2)^(2))=4$ is too much. Which one then?
Knowledgeable students have probably already guessed: in such cases, when it is not possible to solve it “beautifully”, the “heavy artillery” - logarithms - comes into play. Let me remind you that using logarithms, any positive number can be represented as a power of any other positive number (except for one):
Remember this formula? When I tell my students about logarithms, I always warn: this formula (which is also the basic logarithmic identity or, if you like, the definition of a logarithm) will haunt you for a very long time and “pop up” in the most unexpected places. Well, she surfaced. Let's look at our equation and this formula:
\[\begin(align)& ((2)^(x))=3 \\& a=((b)^(((\log )_(b))a)) \\\end(align) \]
If we assume that $a=3$ is our original number on the right, and $b=2$ is the very base of the exponential function to which we so want to reduce the right-hand side, we get the following:
\[\begin(align)& a=((b)^(((\log )_(b))a))\Rightarrow 3=((2)^(((\log )_(2))3 )); \\& ((2)^(x))=3\Rightarrow ((2)^(x))=((2)^(((\log )_(2))3))\Rightarrow x=( (\log )_(2))3. \\\end(align)\]
We received a slightly strange answer: $x=((\log )_(2))3$. In some other task, many would have doubts with such an answer and would begin to double-check their solution: what if an error had crept in somewhere? I hasten to please you: there is no error here, and logarithms in the roots of exponential equations are a completely typical situation. So get used to it. :)
Now let’s solve the remaining two equations by analogy:
\[\begin(align)& ((5)^(x))=15\Rightarrow ((5)^(x))=((5)^(((\log )_(5))15)) \Rightarrow x=((\log )_(5))15; \\& ((4)^(2x))=11\Rightarrow ((4)^(2x))=((4)^(((\log )_(4))11))\Rightarrow 2x=( (\log )_(4))11\Rightarrow x=\frac(1)(2)((\log )_(4))11. \\\end(align)\]
That's all! By the way, the last answer can be written differently:
We introduced a multiplier to the argument of the logarithm. But no one is stopping us from adding this factor to the base:
Moreover, all three options are correct - they are just different forms of writing the same number. Which one to choose and write down in this solution is up to you to decide.
Thus, we have learned to solve any exponential equations of the form $((a)^(x))=b$, where the numbers $a$ and $b$ are strictly positive. However, the harsh reality of our world is that such simple tasks will be encountered very, very rarely. More often than not you will come across something like this:
\[\begin(align)& ((4)^(x))+((4)^(x-1))=((4)^(x+1))-11; \\& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2.7)^(1-x))=0.09. \\\end(align)\]
So how can we solve this? Can this be solved at all? And if so, how?
Don't panic. All these equations quickly and easily reduce to the simple formulas that we have already considered. You just need to remember a couple of tricks from the algebra course. And of course, there are no rules for working with degrees. I'll tell you about all this now. :)
Converting Exponential Equations
The first thing to remember: any exponential equation, no matter how complex it may be, one way or another must be reduced to the simplest equations - the ones that we have already considered and which we know how to solve. In other words, the scheme for solving any exponential equation looks like this:
- Write down the original equation. For example: $((4)^(x))+((4)^(x-1))=((4)^(x+1))-11$;
- Do some weird shit. Or even some crap called "convert an equation";
- At the output, get the simplest expressions of the form $((4)^(x))=4$ or something else like that. Moreover, one initial equation can give several such expressions at once.
Everything is clear with the first point - even my cat can write the equation on a piece of paper. The third point also seems to be more or less clear - we have already solved a whole bunch of such equations above.
But what about the second point? What kind of transformations? Convert what into what? And How?
Well, let's find out. First of all, I would like to note the following. All exponential equations are divided into two types:
- The equation is composed of exponential functions with the same base. Example: $((4)^(x))+((4)^(x-1))=((4)^(x+1))-11$;
- The formula contains exponential functions with different bases. Examples: $((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x))$ and $((100)^(x-1) )\cdot ((2,7)^(1-x))=$0.09.
Let's start with equations of the first type - they are the easiest to solve. And in solving them, we will be helped by such a technique as highlighting stable expressions.
Isolating a stable expression
Let's look at this equation again:
\[((4)^(x))+((4)^(x-1))=((4)^(x+1))-11\]
What do we see? The four are raised to different degrees. But all these powers are simple sums of the variable $x$ with other numbers. Therefore, it is necessary to remember the rules for working with degrees:
\[\begin(align)& ((a)^(x+y))=((a)^(x))\cdot ((a)^(y)); \\& ((a)^(x-y))=((a)^(x)):((a)^(y))=\frac(((a)^(x)))(((a )^(y))). \\\end(align)\]
Simply put, addition can be converted to a product of powers, and subtraction can easily be converted to division. Let's try to apply these formulas to the degrees from our equation:
\[\begin(align)& ((4)^(x-1))=\frac(((4)^(x)))(((4)^(1)))=((4)^ (x))\cdot \frac(1)(4); \\& ((4)^(x+1))=((4)^(x))\cdot ((4)^(1))=((4)^(x))\cdot 4. \ \\end(align)\]
Let's rewrite the original equation taking this fact into account, and then collect all the terms on the left:
\[\begin(align)& ((4)^(x))+((4)^(x))\cdot \frac(1)(4)=((4)^(x))\cdot 4 -eleven; \\& ((4)^(x))+((4)^(x))\cdot \frac(1)(4)-((4)^(x))\cdot 4+11=0. \\\end(align)\]
The first four terms contain the element $((4)^(x))$ - let’s take it out of the bracket:
\[\begin(align)& ((4)^(x))\cdot \left(1+\frac(1)(4)-4 \right)+11=0; \\& ((4)^(x))\cdot \frac(4+1-16)(4)+11=0; \\& ((4)^(x))\cdot \left(-\frac(11)(4) \right)=-11. \\\end(align)\]
It remains to divide both sides of the equation by the fraction $-\frac(11)(4)$, i.e. essentially multiply by the inverted fraction - $-\frac(4)(11)$. We get:
\[\begin(align)& ((4)^(x))\cdot \left(-\frac(11)(4) \right)\cdot \left(-\frac(4)(11) \right )=-11\cdot \left(-\frac(4)(11) \right); \\& ((4)^(x))=4; \\& ((4)^(x))=((4)^(1)); \\& x=1. \\\end(align)\]
That's all! We have reduced the original equation to its simplest form and obtained the final answer.
At the same time, in the process of solving we discovered (and even took it out of the bracket) the common factor $((4)^(x))$ - this is a stable expression. It can be designated as a new variable, or you can simply express it carefully and get the answer. In any case, the key principle of the solution is as follows:
Find in the original equation a stable expression containing a variable that is easily distinguished from all exponential functions.
The good news is that almost every exponential equation allows you to isolate such a stable expression.
But the bad news is that these expressions can be quite tricky and can be quite difficult to identify. So let's look at one more problem:
\[((5)^(x+2))+((0,2)^(-x-1))+4\cdot ((5)^(x+1))=2\]
Perhaps someone will now have a question: “Pasha, are you stoned? There are different bases here – 5 and 0.2.” But let's try converting the power to base 0.2. For example, let’s get rid of the decimal fraction by reducing it to a regular one:
\[((0,2)^(-x-1))=((0,2)^(-\left(x+1 \right)))=((\left(\frac(2)(10 ) \right))^(-\left(x+1 \right)))=((\left(\frac(1)(5) \right))^(-\left(x+1 \right)) )\]
As you can see, the number 5 still appeared, albeit in the denominator. At the same time, the indicator was rewritten as negative. Now let’s remember one of the most important rules for working with degrees:
\[((a)^(-n))=\frac(1)(((a)^(n)))\Rightarrow ((\left(\frac(1)(5) \right))^( -\left(x+1 \right)))=((\left(\frac(5)(1) \right))^(x+1))=((5)^(x+1))\ ]
Here, of course, I was lying a little. Because for a complete understanding, the formula for getting rid of negative indicators had to be written like this:
\[((a)^(-n))=\frac(1)(((a)^(n)))=((\left(\frac(1)(a) \right))^(n ))\Rightarrow ((\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=((\left(\frac(5)(1) \ right))^(x+1))=((5)^(x+1))\]
On the other hand, nothing prevented us from working with just fractions:
\[((\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=((\left(((5)^(-1)) \ right))^(-\left(x+1 \right)))=((5)^(\left(-1 \right)\cdot \left(-\left(x+1 \right) \right) ))=((5)^(x+1))\]
But in this case, you need to be able to raise a power to another power (let me remind you: in this case, the indicators are added together). But I didn’t have to “reverse” the fractions - perhaps this will be easier for some. :)
In any case, the original exponential equation will be rewritten as:
\[\begin(align)& ((5)^(x+2))+((5)^(x+1))+4\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+5\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(1))\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(x+2))=2; \\& 2\cdot ((5)^(x+2))=2; \\& ((5)^(x+2))=1. \\\end(align)\]
So it turns out that the original equation can be solved even more simply than the one previously considered: here you don’t even need to select a stable expression - everything has been reduced by itself. It remains only to remember that $1=((5)^(0))$, from which we get:
\[\begin(align)& ((5)^(x+2))=((5)^(0)); \\& x+2=0; \\& x=-2. \\\end(align)\]
That's the solution! We got the final answer: $x=-2$. At the same time, I would like to note one technique that greatly simplified all calculations for us:
In exponential equations, be sure to get rid of decimal fractions and convert them to ordinary ones. This will allow you to see the same bases of degrees and greatly simplify the solution.
Let us now move on to more complex equations in which there are different bases that cannot be reduced to each other using powers at all.
Using the Degrees Property
Let me remind you that we have two more particularly harsh equations:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2.7)^(1-x))=0.09. \\\end(align)\]
The main difficulty here is that it is not clear what to give and to what basis. Where are the stable expressions? Where are the same grounds? There is none of this.
But let's try to go a different way. If there are no ready-made identical bases, you can try to find them by factoring the existing bases.
Let's start with the first equation:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& 21=7\cdot 3\Rightarrow ((21)^(3x))=((\left(7\cdot 3 \right))^(3x))=((7)^(3x))\ cdot((3)^(3x)). \\\end(align)\]
But you can do the opposite - make the number 21 from the numbers 7 and 3. This is especially easy to do on the left, since the indicators of both degrees are the same:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((\left(7\cdot 3 \right))^(x+ 6))=((21)^(x+6)); \\& ((21)^(x+6))=((21)^(3x)); \\& x+6=3x; \\& 2x=6; \\& x=3. \\\end(align)\]
That's all! You took the exponent outside the product and immediately got a beautiful equation that can be solved in a couple of lines.
Now let's look at the second equation. Everything is much more complicated here:
\[((100)^(x-1))\cdot ((2.7)^(1-x))=0.09\]
\[((100)^(x-1))\cdot ((\left(\frac(27)(10) \right))^(1-x))=\frac(9)(100)\]
In this case, the fractions turned out to be irreducible, but if something could be reduced, be sure to reduce it. Often, interesting reasons will appear with which you can already work.
Unfortunately, nothing special appeared for us. But we see that the exponents on the left in the product are opposite:
Let me remind you: to get rid of the minus sign in the indicator, you just need to “flip” the fraction. Well, let's rewrite the original equation:
\[\begin(align)& ((100)^(x-1))\cdot ((\left(\frac(10)(27) \right))^(x-1))=\frac(9 )(100); \\& ((\left(100\cdot \frac(10)(27) \right))^(x-1))=\frac(9)(100); \\& ((\left(\frac(1000)(27) \right))^(x-1))=\frac(9)(100). \\\end(align)\]
In the second line, we simply took the total exponent out of the product from the bracket according to the rule $((a)^(x))\cdot ((b)^(x))=((\left(a\cdot b \right))^ (x))$, and in the last one they simply multiplied the number 100 by a fraction.
Now note that the numbers on the left (at the base) and on the right are somewhat similar. How? Yes, it’s obvious: they are powers of the same number! We have:
\[\begin(align)& \frac(1000)(27)=\frac(((10)^(3)))(((3)^(3)))=((\left(\frac( 10)(3) \right))^(3)); \\& \frac(9)(100)=\frac(((3)^(2)))(((10)^(3)))=((\left(\frac(3)(10) \right))^(2)). \\\end(align)\]
Thus, our equation will be rewritten as follows:
\[((\left(((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=((\left(\frac(3 )(10)\right))^(2))\]
\[((\left(((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=((\left(\frac(10 )(3) \right))^(3\left(x-1 \right)))=((\left(\frac(10)(3) \right))^(3x-3))\]
In this case, on the right you can also get a degree with the same base, for which it is enough to simply “turn over” the fraction:
\[((\left(\frac(3)(10) \right))^(2))=((\left(\frac(10)(3) \right))^(-2))\]
Our equation will finally take the form:
\[\begin(align)& ((\left(\frac(10)(3) \right))^(3x-3))=((\left(\frac(10)(3) \right)) ^(-2)); \\& 3x-3=-2; \\& 3x=1; \\& x=\frac(1)(3). \\\end(align)\]
That's the solution. His main idea boils down to the fact that even with different bases we try, by hook or by crook, to reduce these bases to the same thing. Elementary transformations of equations and rules for working with powers help us with this.
But what rules and when to use? How do you understand that in one equation you need to divide both sides by something, and in another you need to factor the base of the exponential function?
The answer to this question will come with experience. Try your hand at simple equations first, and then gradually complicate the problems - and very soon your skills will be enough to solve any exponential equation from the same Unified State Exam or any independent/test work.
And to help you in this difficult task, I suggest downloading a set of equations from my website for solving it yourself. All equations have answers, so you can always test yourself.
In general, I wish you a successful training. And see you in the next lesson - there we will analyze really complex exponential equations, where the methods described above are no longer enough. And simple training will not be enough either. :)
Examples:
\(4^x=32\)
\(5^(2x-1)-5^(2x-3)=4.8\)
\((\sqrt(7))^(2x+2)-50\cdot(\sqrt(7))^(x)+7=0\)
How to Solve Exponential Equations
When solving any exponential equation, we strive to bring it to the form \(a^(f(x))=a^(g(x))\), and then make the transition to equality of exponents, that is:
\(a^(f(x))=a^(g(x))\) \(⇔\) \(f(x)=g(x)\)
For example:\(2^(x+1)=2^2\) \(⇔\) \(x+1=2\)
Important! From the same logic, two requirements for such a transition follow:
- number in left and right should be the same;
- the degrees on the left and right must be “pure”, that is, there should be no multiplication, division, etc.
For example:
To reduce the equation to the form \(a^(f(x))=a^(g(x))\) and are used.
Example
. Solve the exponential equation \(\sqrt(27)·3^(x-1)=((\frac(1)(3)))^(2x)\)
Solution:
|
\(\sqrt(27)·3^(x-1)=((\frac(1)(3)))^(2x)\) |
We know that \(27 = 3^3\). Taking this into account, we transform the equation. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(\sqrt(3^3)·3^(x-1)=((\frac(1)(3)))^(2x)\) |
By the property of the root \(\sqrt[n](a)=a^(\frac(1)(n))\) we obtain that \(\sqrt(3^3)=((3^3))^( \frac(1)(2))\). Next, using the property of degree \((a^b)^c=a^(bc)\), we obtain \(((3^3))^(\frac(1)(2))=3^(3 \ cdot \frac(1)(2))=3^(\frac(3)(2))\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(\frac(3)(2))\cdot 3^(x-1)=(\frac(1)(3))^(2x)\) |
We also know that \(a^b·a^c=a^(b+c)\). Applying this to the left side, we get: \(3^(\frac(3)(2))·3^(x-1)=3^(\frac(3)(2)+ x-1)=3^ (1.5 + x-1)=3^(x+0.5)\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(x+0.5)=(\frac(1)(3))^(2x)\) |
Now remember that: \(a^(-n)=\frac(1)(a^n)\). This formula can also be used in the opposite direction: \(\frac(1)(a^n) =a^(-n)\). Then \(\frac(1)(3)=\frac(1)(3^1) =3^(-1)\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(x+0.5)=(3^(-1))^(2x)\) |
Applying the property \((a^b)^c=a^(bc)\) to the right side, we obtain: \((3^(-1))^(2x)=3^((-1) 2x) =3^(-2x)\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(x+0.5)=3^(-2x)\) |
And now our bases are equal and there are no interfering coefficients, etc. So we can make the transition. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Example
. Solve the exponential equation \(4^(x+0.5)-5 2^x+2=0\)
Answer : \(-1; 1\). The question remains - how to understand when to use which method? This comes with experience. Until you have developed it, use the general recommendation for solving complex problems - “if you don’t know what to do, do what you can.” That is, look for how you can transform the equation in principle, and try to do it - what if what happens? The main thing is to make only mathematically based transformations. Exponential equations without solutionsLet's look at two more situations that often confuse students: Let's try to solve by brute force. If x is a positive number, then as x grows, the entire power \(2^x\) will only increase: \(x=1\); \(2^1=2\) \(x=0\); \(2^0=1\) Also by. Negative X's remain. Remembering the property \(a^(-n)=\frac(1)(a^n)\), we check: \(x=-1\); \(2^(-1)=\frac(1)(2^1) =\frac(1)(2)\) Despite the fact that the number becomes smaller with each step, it will never reach zero. So the negative degree did not save us. We come to a logical conclusion: A positive number to any degree will remain a positive number.Thus, both equations above have no solutions. Exponential equations with different basesIn practice, sometimes we encounter exponential equations with different bases that are not reducible to each other, and at the same time with the same exponents. They look like this: \(a^(f(x))=b^(f(x))\), where \(a\) and \(b\) are positive numbers. For example: \(7^(x)=11^(x)\) Such equations can easily be solved by dividing by any of the sides of the equation (usually divided by the right side, that is, by \(b^(f(x))\). You can divide this way because a positive number is positive to any power (that is, we do not divide by zero) We get: \(\frac(a^(f(x)))(b^(f(x)))\) \(=1\) Example
. Solve the exponential equation \(5^(x+7)=3^(x+7)\)
Answer : \(-7\). Sometimes the “sameness” of exponents is not obvious, but skillful use of the properties of exponents resolves this issue. Example
. Solve the exponential equation \(7^( 2x-4)=(\frac(1)(3))^(-x+2)\)
Answer : \(2\). |
Go to the youtube channel of our website to stay up to date with all the new video lessons.
First, let's remember the basic formulas of powers and their properties.
Product of a number a occurs on itself n times, we can write this expression as a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n / a m = a n - m
Power or exponential equations– these are equations in which the variables are in powers (or exponents), and the base is a number.
Examples of exponential equations:
In this example, the number 6 is the base; it is always at the bottom, and the variable x degree or indicator.
Let us give more examples of exponential equations.
2 x *5=10
16 x - 4 x - 6=0
Now let's look at how exponential equations are solved?
Let's take a simple equation:
2 x = 2 3
This example can be solved even in your head. It can be seen that x=3. After all, in order for the left and right sides to be equal, you need to put the number 3 instead of x.
Now let’s see how to formalize this decision:
2 x = 2 3
x = 3
In order to solve such an equation, we removed identical grounds(that is, twos) and wrote down what was left, these are degrees. We got the answer we were looking for.
Now let's summarize our decision.
Algorithm for solving the exponential equation:
1. Need to check the same whether the equation has bases on the right and left. If the reasons are not the same, we are looking for options to solve this example.
2. After the bases become the same, equate degrees and solve the resulting new equation.
Now let's look at a few examples:
Let's start with something simple.
The bases on the left and right sides are equal to the number 2, which means we can discard the base and equate their powers.
x+2=4 The simplest equation is obtained.
x=4 – 2
x=2
Answer: x=2
In the following example you can see that the bases are different: 3 and 9.
3 3x - 9 x+8 = 0
First, move the nine to the right side, we get:
Now you need to make the same bases. We know that 9=3 2. Let's use the power formula (a n) m = a nm.
3 3x = (3 2) x+8
We get 9 x+8 =(3 2) x+8 =3 2x+16
3 3x = 3 2x+16 Now it is clear that on the left and right sides the bases are the same and equal to three, which means we can discard them and equate the degrees.
3x=2x+16 we get the simplest equation
3x - 2x=16
x=16
Answer: x=16.
Let's look at the following example:
2 2x+4 - 10 4 x = 2 4
First of all, we look at the bases, bases two and four. And we need them to be the same. We transform the four using the formula (a n) m = a nm.
4 x = (2 2) x = 2 2x
And we also use one formula a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Add to the equation:
2 2x 2 4 - 10 2 2x = 24
We gave an example for the same reasons. But other numbers 10 and 24 bother us. What to do with them? If you look closely you can see that on the left side we have 2 2x repeated, here is the answer - we can put 2 2x out of brackets:
2 2x (2 4 - 10) = 24
Let's calculate the expression in brackets:
2 4 — 10 = 16 — 10 = 6
We divide the entire equation by 6:
Let's imagine 4=2 2:
2 2x = 2 2 bases are the same, we discard them and equate the degrees.
2x = 2 is the simplest equation. Divide it by 2 and we get
x = 1
Answer: x = 1.
Let's solve the equation:
9 x – 12*3 x +27= 0
Let's transform:
9 x = (3 2) x = 3 2x
We get the equation:
3 2x - 12 3 x +27 = 0
Our bases are the same, equal to three. In this example, you can see that the first three has a degree twice (2x) than the second (just x). In this case, you can solve replacement method. We replace the number with the smallest degree:
Then 3 2x = (3 x) 2 = t 2
We replace all x powers in the equation with t:
t 2 - 12t+27 = 0
We get a quadratic equation. Solving through the discriminant, we get:
D=144-108=36
t 1 = 9
t2 = 3
Returning to the variable x.
Take t 1:
t 1 = 9 = 3 x
That is,
3 x = 9
3 x = 3 2
x 1 = 2
One root was found. We are looking for the second one from t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Answer: x 1 = 2; x 2 = 1.
On the website you can ask any questions you may have in the HELP DECIDE section, we will definitely answer you.
Join the group
This is the name for equations of the form where the unknown is in both the exponent and the base of the power.
You can specify a completely clear algorithm for solving an equation of the form. To do this, you need to pay attention to the fact that when Oh) not equal to zero, one and minus one, equality of degrees with the same bases (be it positive or negative) is possible only if the exponents are equal. That is, all the roots of the equation will be the roots of the equation f(x) = g(x) The converse statement is not true, when Oh)< 0 and fractional values f(x) And g(x) expressions Oh) f(x) And
Oh) g(x) lose their meaning. That is, when moving from to f(x) = g(x)(for and extraneous roots may appear, which must be excluded by checking against the original equation. And cases a = 0, a = 1, a = -1 need to be considered separately.
So, to completely solve the equation, we consider the cases:
a(x) = O f(x) And g(x) will be positive numbers, then this is the solution. Otherwise, no
a(x) = 1. The roots of this equation are also the roots of the original equation.
a(x) = -1. If, for a value of x that satisfies this equation, f(x) And g(x) are integers of the same parity (either both even or both odd), then this is the solution. Otherwise, no
When and we solve the equation f(x)= g(x) and by substituting the obtained results into the original equation we cut off the extraneous roots.
Examples of solving exponential-power equations.
Example No. 1.
1) x - 3 = 0, x = 3. because 3 > 0, and 3 2 > 0, then x 1 = 3 is the solution.
2) x - 3 = 1, x 2 = 4.
3) x - 3 = -1, x = 2. Both indicators are even. This solution is x 3 = 1.
4) x - 3 ? 0 and x? ± 1. x = x 2, x = 0 or x = 1. For x = 0, (-3) 0 = (-3) 0 - this solution is correct: x 4 = 0. For x = 1, (-2) 1 = (-2) 1 - this solution is correct x 5 = 1.
Answer: 0, 1, 2, 3, 4.
Example No. 2.

By definition of an arithmetic square root: x - 1? 0, x ? 1.
1) x - 1 = 0 or x = 1, = 0, 0 0 is not a solution.
2) x - 1 = 1 x 1 = 2.
3) x - 1 = -1 x 2 = 0 does not fit in ODZ.
D = (-2) - 4*1*5 = 4 - 20 = -16 - there are no roots.
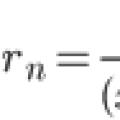 Taylor series expansion Approximate solution of the Cauchy problem for the ordinary
Taylor series expansion Approximate solution of the Cauchy problem for the ordinary What is NOT taught at school What is not taught at school ask
What is NOT taught at school What is not taught at school ask Money Thinking Formula (A
Money Thinking Formula (A