The main property of an algebraic fraction: formulation, proof, application examples. The main property of an algebraic fraction Fractions and their properties
When studying ordinary fractions, we come across the concepts of the basic properties of a fraction. A simplified formulation is necessary to solve examples with ordinary fractions. This article involves the consideration of algebraic fractions and the application of a basic property to them, which will be formulated with examples of the scope of its application.
Formulation and rationale
The main property of a fraction has the form:
Definition 1
When the numerator and denominator are simultaneously multiplied or divided by the same number, the value of the fraction remains unchanged.
That is, we get that a · m b · m = a b and a: m b: m = a b are equivalent, where a b = a · m b · m and a b = a: m b: m are considered fair. The values a, b, m are some natural numbers.
Dividing the numerator and denominator by a number can be represented as a · m b · m = a b . This is similar to solving the example 8 12 = 8: 4 12: 4 = 2 3. When dividing, an equality of the form a: m b is used: m = a b, then 8 12 = 2 · 4 2 · 4 = 2 3. It can also be represented in the form a · m b · m = a b, that is, 8 12 = 2 · 4 3 · 4 = 2 3.
That is, the main property of the fraction a · m b · m = a b and a b = a · m b · m will be considered in detail in contrast to a: m b: m = a b and a b = a: m b: m.
If the numerator and denominator contain real numbers, then the property is applicable. First you need to prove the validity of the written inequality for all numbers. That is, prove the existence of a · m b · m = a b for all real a , b , m , where b and m are nonzero values to avoid division by zero.
Evidence 1
Let a fraction of the form a b be considered part of the record z, in other words, a b = z, then it is necessary to prove that a · m b · m corresponds to z, that is, prove a · m b · m = z. Then this will allow us to prove the existence of the equality a · m b · m = a b .
The fraction line represents the division sign. Applying the connection with multiplication and division, we find that from a b = z after transformation we obtain a = b · z. According to the properties of numerical inequalities, both sides of the inequality should be multiplied by a number other than zero. Then we multiply by the number m, we get that a · m = (b · z) · m. By property, we have the right to write the expression in the form a · m = (b · m) · z. This means that from the definition it follows that a b = z. That's all the proof of the expression a · m b · m = a b .
Equalities of the form a · m b · m = a b and a b = a · m b · m make sense when instead of a , b , m there are polynomials, and instead of b and m they are non-zero.
The main property of an algebraic fraction: when we simultaneously multiply the numerator and denominator by the same number, we obtain an expression identical to the original one.
The property is considered valid, since actions with polynomials correspond to actions with numbers.
Example 1
Let's look at the example of the fraction 3 · x x 2 - x y + 4 · y 3. It is possible to convert to the form 3 · x · (x 2 + 2 · x · y) (x 2 - x y + 4 · y 3) · (x 2 + 2 · x · y).
Multiplication by the polynomial x 2 + 2 · x · y was performed. In the same way, the main property helps to get rid of x 2, present in a given fraction of the form 5 x 2 (x + 1) x 2 (x 3 + 3) to the form 5 x + 5 x 3 + 3. This is called simplification.
The main property can be written as expressions a · m b · m = a b and a b = a · m b · m, when a, b, m are polynomials or ordinary variables, and b and m must be non-zero.
Areas of application of the basic property of an algebraic fraction
The application of the main property is relevant for reduction to a new denominator or when reducing a fraction.
Definition 2
Reducing to a common denominator is multiplying the numerator and denominator by a similar polynomial to obtain a new one. The resulting fraction is equal to the original one.
That is, a fraction of the form x + y · x 2 + 1 (x + 1) · x 2 + 1 when multiplied by x 2 + 1 and reduced to a common denominator (x + 1) · (x 2 + 1) will receive the form x 3 + x + x 2 · y + y x 3 + x + x 2 + 1 .
After carrying out operations with polynomials, we find that the algebraic fraction is transformed into x 3 + x + x 2 · y + y x 3 + x + x 2 + 1.
Reduction to a common denominator is also performed when adding or subtracting fractions. If fractional coefficients are given, then a simplification must first be made, which will simplify the appearance and the very determination of the common denominator. For example, 2 5 x y - 2 x + 1 2 = 10 2 5 x y - 2 10 x + 1 2 = 4 x y - 20 10 x + 5.
The application of the property when reducing fractions is carried out in 2 stages: decomposition of the numerator and denominator into factors to find the common m, and then proceed to the type of fraction a b, based on an equality of the form a · m b · m = a b.
If a fraction of the form 4 x 3 - x y 16 x 4 - y 2 after expansion is transformed into x (4 x 2 - y) 4 x 2 - y 4 x 2 + y, it is obvious that the general the multiplier will be the polynomial 4 x 2 − y. Then it will be possible to reduce the fraction according to its main property. We get that
x (4 x 2 - y) 4 x 2 - y 4 x 2 + y = x 4 x 2 + y. The fraction is simplified, then when substituting values it will be necessary to perform much less action than when substituting into the original one.
If you notice an error in the text, please highlight it and press Ctrl+Enter
In mathematics, a fraction is a number consisting of one or more parts (fractions) of a unit. According to the form of recording, fractions are divided into ordinary (example \frac(5)(8)) and decimal (for example 123.45).
Definition. Common fraction (or simple fraction)
Ordinary (simple) fraction is called a number of the form \pm\frac(m)(n) where m and n are natural numbers. The number m is called numerator this fraction, and the number n is its denominator.
A horizontal or slash indicates a division sign, that is, \frac(m)(n)=()^m/n=m:n
Common fractions are divided into two types: proper and improper.
Definition. Proper and improper fractions
Correct A fraction whose numerator is less than its denominator is called a fraction. For example, \frac(9)(11) , because 9
Wrong A fraction is called in which the modulus of the numerator is greater than or equal to the modulus of the denominator. Such a fraction is a rational number with a modulus greater than or equal to one. An example would be the fractions \frac(11)(2) , \frac(2)(1) , -\frac(7)(5) , \frac(1)(1)
Along with the improper fraction, there is another representation of the number, which is called a mixed fraction (mixed number). This is not an ordinary fraction.
Definition. Mixed fraction (mixed number)
Mixed fraction is a fraction written as a whole number and a proper fraction and is understood as the sum of this number and the fraction. For example, 2\frac(5)(7)
(written as a mixed number) 2\frac(5)(7)=2+\frac(5)(7)=\frac(14)(7)+\frac(5)(7)=\frac(19 )(7) (written as an improper fraction)
A fraction is just a representation of a number. The same number can correspond to different fractions, both ordinary and decimal. Let us form a sign for the equality of two ordinary fractions.
Definition. Sign of equality of fractions
The two fractions \frac(a)(b) and \frac(c)(d) are equal, if a\cdot d=b\cdot c . For example, \frac(2)(3)=\frac(8)(12) since 2\cdot12=3\cdot8
From this attribute follows the main property of a fraction.
Property. The main property of a fraction
If the numerator and denominator of a given fraction are multiplied or divided by the same number, not equal to zero, you get a fraction equal to the given one.
\frac(A)(B)=\frac(A\cdot C)(B\cdot C)=\frac(A:K)(B:K);\quad C \ne 0,\quad K \ne 0
Using the basic property of a fraction, you can replace a given fraction with another fraction that is equal to the given one, but with a smaller numerator and denominator. This replacement is called fraction reduction. For example, \frac(12)(16)=\frac(6)(8)=\frac(3)(4) (here the numerator and denominator were divided first by 2, and then by 2 more). A fraction can be reduced if and only if its numerator and denominator are not mutually prime numbers. If the numerator and denominator of a given fraction are mutually prime, then the fraction cannot be reduced, for example, \frac(3)(4) is an irreducible fraction.
Rules for positive fractions:
From two fractions with the same denominators The fraction whose numerator is greater is greater. For example, \frac(3)(15)
From two fractions with the same numerators The larger is the fraction whose denominator is smaller. For example, \frac(4)(11)>\frac(4)(13) .
To compare two fractions with different numerators and denominators, you must convert both fractions so that their denominators are the same. This transformation is called reducing fractions to a common denominator.
This topic is quite important; all further mathematics and algebra are based on the basic properties of fractions. The properties of fractions considered, despite their importance, are very simple.
To understand basic properties of fractions Let's consider a circle.
On the circle you can see that 4 parts or are shaded out of the possible eight. Let's write the resulting fraction \(\frac(4)(8)\)

On the next circle you can see that one of the two possible parts is shaded. Let's write the resulting fraction \(\frac(1)(2)\)
If we look closely, we will see that in the first case, that in the second case we have half the circle shaded, so the resulting fractions are equal to \(\frac(4)(8) = \frac(1)(2)\), that is it's the same number.
How to prove this mathematically? It’s very simple, remember the multiplication table and write the first fraction into factors.
\(\frac(4)(8) = \frac(1 \cdot \color(red) (4))(2 \cdot \color(red) (4)) = \frac(1)(2) \cdot \color(red) (\frac(4)(4)) =\frac(1)(2) \cdot \color(red)(1) = \frac(1)(2)\)
What have we done? We factored the numerator and denominator \(\frac(1 \cdot \color(red) (4))(2 \cdot \color(red) (4))\), and then divided the fractions \(\frac(1) (2) \cdot \color(red) (\frac(4)(4))\). Four divided by four is 1, and one multiplied by any number is the number itself. What we did in the above example is called reducing fractions.
Let's look at another example and reduce the fraction.
\(\frac(6)(10) = \frac(3 \cdot \color(red) (2))(5 \cdot \color(red) (2)) = \frac(3)(5) \cdot \color(red) (\frac(2)(2)) =\frac(3)(5) \cdot \color(red)(1) = \frac(3)(5)\)
We again factored the numerator and denominator and reduced the same numbers into numerators and denominators. That is, two divided by two gives one, and one multiplied by any number gives the same number.
The main property of a fraction.
This implies the main property of a fraction:
If both the numerator and the denominator of a fraction are multiplied by the same number (except zero), then the value of the fraction will not change.
\(\bf \frac(a)(b) = \frac(a \cdot n)(b \cdot n)\)
You can also divide the numerator and denominator by the same number at the same time.
Let's look at an example:
\(\frac(6)(8) = \frac(6 \div \color(red) (2))(8 \div \color(red) (2)) = \frac(3)(4)\)
If both the numerator and denominator of a fraction are divided by the same number (except zero), then the value of the fraction will not change.
\(\bf \frac(a)(b) = \frac(a \div n)(b \div n)\)
Fractions that have common prime factors in both numerators and denominators are called reducible fractions.
Example of a reducible fraction: \(\frac(2)(4), \frac(6)(10), \frac(9)(15), \frac(10)(5), …\)
There is also irreducible fractions.
Irreducible fraction is a fraction that does not have common prime factors in its numerators and denominators.
Example of an irreducible fraction: \(\frac(1)(2), \frac(3)(5), \frac(5)(7), \frac(13)(5), …\)
Any number can be expressed as a fraction because any number is divisible by one. For example:
\(7 = \frac(7)(1)\)
Questions to the topic:
Do you think any fraction can be reduced or not?
Answer: no, there are reducible fractions and irreducible fractions.
Check whether the equality is true: \(\frac(7)(11) = \frac(14)(22)\)?
Answer: write the fraction \(\frac(14)(22) = \frac(7 \cdot 2)(11 \cdot 2) = \frac(7)(11)\), yes that's fair.
Example #1:
a) Find a fraction with a denominator of 15 equal to the fraction \(\frac(2)(3)\).
b) Find a fraction with numerator 8 that is equal to the fraction \(\frac(1)(5)\).
Solution:
a) We need the number 15 in the denominator. Now the denominator has the number 3. What number should we multiply the number 3 by to get 15? Let's remember the multiplication table 3⋅5. We need to use the basic property of fractions and multiply both the numerator and the denominator of the fraction \(\frac(2)(3)\) by 5.
\(\frac(2)(3) = \frac(2 \cdot 5)(3 \cdot 5) = \frac(10)(15)\)
b) We need the number 8 to be in the numerator. Now the number 1 is in the numerator. What number should we multiply the number 1 by to get 8? Of course, 1⋅8. We need to use the basic property of fractions and multiply both the numerator and the denominator of the fraction \(\frac(1)(5)\) by 8. We get:
\(\frac(1)(5) = \frac(1 \cdot 8)(5 \cdot 8) = \frac(8)(40)\)
Example #2:
Find an irreducible fraction equal to the fraction: a) \(\frac(16)(36)\), b) \(\frac(10)(25)\).
Solution:
A) \(\frac(16)(36) = \frac(4 \cdot 4)(9 \cdot 4) = \frac(4)(9)\)
b) \(\frac(10)(25) = \frac(2 \cdot 5)(5 \cdot 5) = \frac(2)(5)\)
Example #3:
Write the number as a fraction: a) 13 b)123
Solution:
A) \(13 = \frac(13) (1)\)
b) \(123 = \frac(123) (1)\)
Fraction- a form of representing a number in mathematics. The fraction bar denotes the division operation. Numerator fraction is called the dividend, and denominator- divider. For example, in a fraction the numerator is 5 and the denominator is 7.
Correct A fraction is called in which the modulus of the numerator is greater than the modulus of the denominator. If a fraction is proper, then the modulus of its value is always less than 1. All other fractions are wrong.
The fraction is called mixed, if it is written as an integer and a fraction. This is the same as the sum of this number and the fraction:
The main property of a fraction
If the numerator and denominator of a fraction are multiplied by the same number, then the value of the fraction will not change, that is, for example,
![]()
Reducing fractions to a common denominator
To bring two fractions to a common denominator, you need:
- Multiply the numerator of the first fraction by the denominator of the second
- Multiply the numerator of the second fraction by the denominator of the first
- Replace the denominators of both fractions with their product
Operations with fractions
Addition. To add two fractions you need
- Add the new numerators of both fractions and leave the denominator unchanged
Example:
Subtraction. To subtract one fraction from another, you need
- Reduce fractions to a common denominator
- Subtract the numerator of the second from the numerator of the first fraction, and leave the denominator unchanged
Example:
![]()
Multiplication. To multiply one fraction by another, multiply their numerators and denominators.
Discussed in detail main property of a fraction, its formulation is given, a proof and an explanatory example are given. The application of the basic property of a fraction when reducing fractions and reducing fractions to a new denominator is also considered.
Page navigation.
The main property of a fraction - formulation, proof and explanatory examples
Let's look at an example that illustrates the basic property of a fraction. Let's say we have a square divided into 9 "big" squares, and each of these "big" squares is divided into 4 "small" squares. Thus, we can also say that the original square is divided into 4 9 = 36 “small” squares. Let's paint 5 “big” squares. In this case, 4·5=20 “small” squares will be shaded. Here is a drawing that corresponds to our example.

The shaded part is 5/9 of the original square, or, which is the same, 20/36 of the original square, that is, the fractions 5/9 and 20/36 are equal: or. From these equalities, as well as from the equalities 20=5·4, 36=9·4, 20:4=5 and 36:4=9, it follows that and .
To consolidate the disassembled material, consider the solution to the example.
Example.
Numerator and denominator of some common fraction multiplied by 62, after which the numerator and denominator of the resulting fraction were divided by 2. Is the resulting fraction equal to the original one?
Solution.
Multiplying the numerator and denominator of a fraction by any natural number, in particular at 62, gives a fraction, which, due to the basic property of the fraction, is equal to the original one. The main property of a fraction allows us to state that after dividing the numerator and denominator of the resulting fraction by 2, the resulting fraction will be equal to the original fraction.
Answer:
Yes, the resulting fraction is equal to the original one.
Application of the basic property of a fraction
The basic property of a fraction is mainly used in two cases: firstly, when reducing fractions to a new denominator, and secondly, when reducing fractions.
The main property of a fraction allows you to reduce fractions, and as a result move from the original fraction to an equal fraction, but with a smaller numerator and denominator. Reducing a fraction consists of dividing the numerator and denominator of the original fraction by any positive numerator and denominator other than one (if there are no such common divisors, then the original fraction is irreducible, that is, cannot be reduced). In particular, dividing by will reduce the original fraction to an irreducible form.
Bibliography.
- Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S., Shvartsburd S.I. Mathematics: textbook for 5th grade. educational institutions.
- Vilenkin N.Ya. and others. Mathematics. 6th grade: textbook for general education institutions.
Copyright by cleverstudents
All rights reserved.
Protected by copyright law. No part of the site, including internal materials and appearance, may be reproduced in any form or used without the prior written permission of the copyright holder.
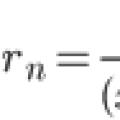 Taylor series expansion Approximate solution of the Cauchy problem for the ordinary
Taylor series expansion Approximate solution of the Cauchy problem for the ordinary What is NOT taught at school What is not taught at school ask
What is NOT taught at school What is not taught at school ask Money Thinking Formula (A
Money Thinking Formula (A