Integral types and solution methods. Integration by change of variable method
A function F(x) differentiable in a given interval X is called antiderivative of the function f(x), or the integral of f(x), if for every x ∈X the following equality holds:
F " (x) = f(x). (8.1)
Finding all antiderivatives for a given function is called its integration. Indefinite integral function f(x) on a given interval X is the set of all antiderivative functions for the function f(x); designation -
If F(x) is some antiderivative of the function f(x), then ∫ f(x)dx = F(x) + C, (8.2)
where C is an arbitrary constant.
Table of integrals
Directly from the definition we obtain the main properties Not definite integral and a list of tabular integrals:
1) d∫f(x)dx=f(x)
2)∫df(x)=f(x)+C
3) ∫af(x)dx=a∫f(x)dx (a=const)
4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx
List of tabular integrals
1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)
3.∫a x dx = a x /ln a + C (a>0, a ≠1)
4.∫e x dx = e x + C
5.∫sin x dx = cosx + C
6.∫cos x dx = - sin x + C
7. = arctan x + C
8. = arcsin x + C
10. = - ctg x + C
Variable replacement
To integrate many functions, use the variable replacement method or substitutions, allowing you to reduce integrals to tabular form.
If the function f(z) is continuous on [α,β], the function z =g(x) has a continuous derivative and α ≤ g(x) ≤ β, then
∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)
Moreover, after integration on the right side, the substitution z=g(x) should be made.
To prove it, it is enough to write the original integral in the form:
∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).
For example:
Method of integration by parts
Let u = f(x) and v = g(x) be functions that have continuous . Then, according to the work,
d(uv))= udv + vdu or udv = d(uv) - vdu.
For the expression d(uv), the antiderivative will obviously be uv, so the formula holds:
∫ udv = uv - ∫ vdu (8.4.)
This formula expresses the rule integration by parts. It leads the integration of the expression udv=uv"dx to the integration of the expression vdu=vu"dx.
Let, for example, you want to find ∫xcosx dx. Let us put u = x, dv = cosxdx, so du=dx, v=sinx. Then
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
The rule of integration by parts has a more limited scope than substitution of variables. But there are whole classes of integrals, for example,
∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax and others, which are calculated precisely using integration by parts.
Definite integral
The concept of a definite integral is introduced as follows. Let a function f(x) be defined on an interval. Let us divide the segment [a,b] into n parts by points a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 ,
x i) возьмем произвольную точку ξ i и составим сумму f(ξ i)
Δx i где
Δ x i =x i - x i-1. A sum of the form f(ξ i)Δ x i is called integral sum, and its limit at λ = maxΔx i → 0, if it exists and is finite, is called definite integral functions f(x) of a before b and is designated:
F(ξ i)Δx i (8.5).
The function f(x) in this case is called integrable on the interval, numbers a and b are called lower and upper limits of the integral.
The following properties are true for a definite integral:
4), (k = const, k∈R);
5)![]()
6)![]()
7) f(ξ)(b-a) (ξ∈).
The last property is called mean value theorem.
Let f(x) be continuous on . Then on this segment there is an indefinite integral
∫f(x)dx = F(x) + C
and takes place Newton-Leibniz formula, connecting the definite integral with the indefinite integral:
F(b) - F(a). (8.6)
Geometric interpretation: the definite integral is the area of a curvilinear trapezoid bounded from above by the curve y=f(x), straight lines x = a and x = b and a segment of the axis Ox.
Improper integrals
Integrals with infinite limits and integrals of discontinuous (unbounded) functions are called not your own. Improper integrals of the first kind - These are integrals over an infinite interval, defined as follows:
![]() (8.7)
(8.7)
If this limit exists and is finite, then it is called convergent improper integral of f(x) on the interval [a,+ ∞), and the function f(x) is called integrable over an infinite interval[a,+ ∞). Otherwise, the integral is said to be does not exist or diverges.
Improper integrals on the intervals (-∞,b] and (-∞, + ∞) are defined similarly:
Let us define the concept of an integral of an unbounded function. If f(x) is continuous for all values x segment , except for the point c, at which f(x) has an infinite discontinuity, then improper integral of the second kind of f(x) ranging from a to b the amount is called:
![]()
if these limits exist and are finite. Designation:
Examples of integral calculations
Example 3.30. Calculate ∫dx/(x+2).
Solution. Let us denote t = x+2, then dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.
Example 3.31. Find ∫ tgxdx.
Solution.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Let t=cosx, then ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.
Example3.32 . Find ∫dx/sinxSolution.
Example3.33. Find .
Solution. = .
Example3.34 . Find ∫arctgxdx.
Solution. Let's integrate by parts. Let us denote u=arctgx, dv=dx. Then du = dx/(x 2 +1), v=x, whence ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; because
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.
Example3.35 . Calculate ∫lnxdx.
Solution. Applying the integration by parts formula, we obtain:
u=lnx, dv=dx, du=1/x dx, v=x. Then ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.
Example3.36 . Calculate ∫e x sinxdx.
Solution. Let us denote u = e x, dv = sinxdx, then du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. We also integrate the integral ∫e x cosxdx by parts: u = e x , dv = cosxdx, du=e x dx, v=sinx. We have:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. We obtained the relation ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, from which 2∫e x sinx dx = - e x cosx + e x sinx + C.
Example 3.37. Calculate J = ∫cos(lnx)dx/x.
Solution. Since dx/x = dlnx, then J= ∫cos(lnx)d(lnx). Replacing lnx through t, we arrive at the table integral J = ∫ costdt = sint + C = sin(lnx) + C.
Example 3.38 . Calculate J = .
Solution. Considering that = d(lnx), we substitute lnx = t. Then J = ![]() .
.
Example 3.39
. Calculate the integral J = ![]() .
.
Solution. We have: ![]() . Therefore =
. Therefore =
=
=. entered like this: sqrt(tan(x/2)).
And if in the result window you click on Show steps in the upper right corner, you will get a detailed solution.
Solving integrals is an easy task, but only for a select few. This article is for those who want to learn to understand integrals, but know nothing or almost nothing about them. Integral... Why is it needed? How to calculate it? What are definite and indefinite integrals? If the only use you know of for an integral is to use a crochet hook shaped like an integral icon to get something useful out of hard-to-reach places, then welcome! Find out how to solve integrals and why you can't do without it.
We study the concept of "integral"
Integration was known back in Ancient Egypt. Of course, not in its modern form, but still. Since then, mathematicians have written many books on this topic. Especially distinguished themselves Newton And Leibniz , but the essence of things has not changed. How to understand integrals from scratch? No way! To understand this topic, you will still need a basic knowledge of the basics of mathematical analysis. We already have information about , necessary for understanding integrals, on our blog.
Indefinite integral
Let us have some function f(x) .
Indefinite integral function f(x) this function is called F(x) , whose derivative is equal to the function f(x) .
In other words, an integral is a derivative in reverse or an antiderivative. By the way, read about how in our article.

An antiderivative exists for all continuous functions. Also, a constant sign is often added to the antiderivative, since the derivatives of functions that differ by a constant coincide. The process of finding the integral is called integration.
Simple example:

In order not to constantly calculate antiderivatives of elementary functions, it is convenient to put them in a table and use ready-made values.
Complete table of integrals for students

Definite integral
When dealing with the concept of an integral, we are dealing with infinitesimal quantities. The integral will help to calculate the area of a figure, the mass of a non-uniform body, the distance traveled during uneven movement, and much more. It should be remembered that an integral is the sum of an infinitely large number of infinitesimal terms.
As an example, imagine a graph of some function. How to find the area of a figure bounded by the graph of a function?

Using an integral! Let us divide the curvilinear trapezoid, limited by the coordinate axes and the graph of the function, into infinitesimal segments. This way the figure will be divided into thin columns. The sum of the areas of the columns will be the area of the trapezoid. But remember that such a calculation will give an approximate result. However, the smaller and narrower the segments, the more accurate the calculation will be. If we reduce them to such an extent that the length tends to zero, then the sum of the areas of the segments will tend to the area of the figure. This is a definite integral, which is written like this:

Points a and b are called limits of integration.
 Bari Alibasov and the group "Integral"
Bari Alibasov and the group "Integral" By the way! For our readers there is now a 10% discount on
Rules for calculating integrals for dummies
Properties of the indefinite integral
How to solve an indefinite integral? Here we will look at the properties of the indefinite integral, which will be useful when solving examples.
- The derivative of the integral is equal to the integrand:

- The constant can be taken out from under the integral sign:

- The integral of the sum is equal to the sum of the integrals. This is also true for the difference:
Properties of a definite integral
- Linearity:

- The sign of the integral changes if the limits of integration are swapped:

- At any points a, b And With:

We have already found out that a definite integral is the limit of a sum. But how to get a specific value when solving an example? For this there is the Newton-Leibniz formula:

Examples of solving integrals
Below we will consider several examples of finding indefinite integrals. We suggest you figure out the intricacies of the solution yourself, and if something is unclear, ask questions in the comments.

To reinforce the material, watch a video about how integrals are solved in practice. Don't despair if the integral is not given right away. Contact a professional service for students, and any triple or curved integral over a closed surface will be within your power.
Direct integration
Basic integration formulas
| 1. C – constant | 1*. | |
| 2. , n ≠ –1 | ||
| 3. +C | ||
| 4. | ||
| 5. | ||
| 6. | ||
| 7. | ||
| 8. | ||
| 9. | ||
| 10. | ||
| 11. | ||
| 12. | ||
| 13. | ||
| 14. |
Calculation of integrals by direct use of the table of simple integrals and the basic properties of indefinite integrals is called direct integration.
Example 1.
Example 2.
Example 3.
This is the most common method of integrating a complex function, consisting of transforming the integral by moving to another integration variable.
If it is difficult to reduce the integral to a tabular one using elementary transformations, then in this case the substitution method is used. The essence of this method is that by introducing a new variable it is possible to reduce this integral to a new integral, which is relatively easy to take directly.
To integrate by substitution method, use the solution scheme:
2) find the differential from both replacement parts;
3) express the entire integrand through a new variable (after which a table integral should be obtained);
4) find the resulting table integral;
5) perform a reverse replacement.
Find the integrals:
Example 1 . Substitution:cosx=t,-sinxdx=dt,
Solution:
Example 2.∫e -x3 x 2 dx Substitution:-x 3 =t, -3x 2 dx=dt, Solution:∫e -x3 x 2 dx=∫e t (-1/3)dt=-1/3e t +C=-1/3e -x3 +C
Example 3.Substitution: 1+sinx=t , cosxdx=dt ,
Solution: .
SECTION 1.5. Definite integral, methods of its calculation.
item 1 The concept of a definite integral
Task. Find the increment of a function that is antiderivative of a function f(x), when passing the argument x from the value a to value b.
Solution. Let us assume that integration has found: ∫ (x)dx = F(x)+C.
Then F(x)+C 1, Where C 1- any given number will be one of the antiderivative functions for this function f(x). Let's find its increment when the argument moves from the value a to value b. We get:
x=b - x=a =F(b) +C 1 - F(a) -C 1 =F(b)-F(a)
As we see, in the expression for the increment of the antiderivative function F(x)+C 1 no constant value C 1. And since under C 1 any given number was implied, the result obtained leads to the following conclusion: on argument transition x from the value x=a to value x=b all functions F(x)+C, antiderivatives for a given function f(x), have the same increment equal to F(b)-F(a).
This increment is usually called the definite integral and denoted by the symbol: and read: integral of A before b from the function f(x) over dх or, in short, the integral of A before b from f(x)dx.
Number A called lower limit integration, number b - top; segment a ≤ x ≤ b – segment of integration. It is assumed that the integrand function f(x) continuous for all values x, satisfying the conditions: a x b
Definition. Increment of antiderivative functions F(x)+C on argument transition x from the value x=a to value x=b, equal to the difference F(b)-F(a), is called a definite integral and is denoted by the symbol: so that if ∫ (x)dx = F(x)+C, then = F(b)-F(a) - given the equality is called the Newton-Leibniz formula.
item 2 Basic properties of the definite integral
All properties are formulated in the proposition that the functions under consideration are integrable in the corresponding intervals.
item 3 Direct calculation of the definite integral
To calculate the definite integral, when you can find the corresponding indefinite integral, use the Newton–Leibniz formula
those. the definite integral is equal to the difference between the values of any antiderivative function at the upper and lower limits of integration.
This formula shows the procedure for calculating a definite integral:
1) find the indefinite integral of this function;
2) into the resulting antiderivative, substitute first the upper and then the lower limit of the integral instead of the argument;
3) subtract the result of substituting the lower limit from the result of substituting the upper limit.
Example 1: Calculate the integral:
Example 2: Calculate the integral:
p.4 Calculation of a definite integral by substitution method
The calculation of the definite integral by the substitution method is as follows:
1) replace part of the integrand with a new variable;
2) find new limits of the definite integral;
3) find the differential from both replacement parts;
4) express the entire integrand through a new variable (after which a table integral should be obtained); 5) calculate the resulting definite integral.
Example 1: Calculate the integral:
Substitution: 1+cosx=t,-sinxdx=dt,
SECTION 1.6. Geometric meaning of a definite integral.
Area of a curved trapezoid:
It is known that a definite integral on a segment represents the area of a curvilinear trapezoid bounded by the graph of the function f(x).
The area of a figure bounded by certain lines can be found using certain integrals if the equations of these lines are known.
Let on the segment [a; b] a continuous function is given y = ƒ(x) ≥ 0. Let us find the area of this trapezoid.
Area of the figure bounded by axis 0 x, two vertical straight lines x = a, x = b and the graph of the function y = ƒ(x) (figure), determined by the formula:
This is the geometric meaning of the definite integral.
Example 1: Calculate the area of the figure bounded by the lines: y=x2.+2, y=0, x= -2, x=1.
Solution: Let's make a drawing (note that the equation y=0 defines the Ox axis).
Answer: S = 9 units 2
Example 2: Calculate the area of the figure bounded by the lines: y= - e x, x=1 and coordinate axes.
Solution: Let's make a drawing.
If a curved trapezoid completely located under the Ox axis, then its area can be found using the formula:
In this case:
Attention! If you are asked to find the area of a figure using a definite integral, then the area is always positive! That is why the minus appears in the formula just discussed.
SECTION 1.7. Application of the definite integral
p.1 Calculation of the volume of a body of revolution
If a curved trapezoid is adjacent to the Ox axis, and straight lines y=a, y=b and the graph of the function y= F(x) (Fig. 1), then the volume of the body of revolution is determined by a formula containing an integral.
The volume of the body of revolution is equal to:
Example:
Find the volume of the body limited by the surface of rotation of the line around the Ox axis at 0≤ x ≤4.
Solution: V
units 3. Answer: unit 3.
SECTION 3.1. Ordinary differential equations
item 1 The concept of a differential equation
Definition. Differential equation is an equation containing a function of a set of variables and their derivatives.
The general form of such an equation is =0, where F is a known function of its arguments, specified in a fixed domain; x - independent variable (variable by which it is differentiated); y - dependent variable (the one from which derivatives are taken and the one to be determined); - derivative of the dependent variable y with respect to the independent variable x.
item 2 Basic concepts of differential equation
In order of a differential equation is called the order of the highest derivative included in it.
For example:
A second order equation is a first order equation.
Any function that connects variables and turns a differential equation into a true equality is called decision differential equation.
General solution of a first-order differential equation is a function of and an arbitrary constant C that turns this equation into an identity in .
The general solution, written in the implicit form =0, is called general integral.
Private decision equation =0 is a solution obtained from the general solution for a fixed value - a fixed number.
The problem of finding a particular solution to a differential equation of the nth order (n= 1,2,3,...), satisfying the initial conditions of the form
called Cauchy problem.
item 3 First order differential equations with separable variables
A first-order differential equation is called a separable equation if it can be represented as can be rewritten as . If . Let's integrate: .
To solve an equation of this type you need:
1. Separate variables;
2. By integrating the equation with separated variables, find the general solution of this equation;
3. Find a particular solution that satisfies the initial conditions (if they are given).
Example 1. Solve the equation. Find a particular solution that satisfies the condition y=4 at x=-2.
Solution: This is a separated variable equation. Integrating, we find the general solution to the equation: . To obtain a simpler general solution, we represent the constant term on the right side in the form C/2. We have or is a general solution. Substituting the values y=4 and x=-2 into the general solution, we get 16=4+C, from which C=12.
So, a particular solution of the equation that satisfies this condition has the form
Example 2. Find a particular solution to the equation if .
Solution:, , , , , common decision.
We substitute the values of x and y into the private solution: , , private solution.
Example 3. Find the general solution to the equation . Solution: ,, , - common decision.
item 4 Differential equations of order higher than the first
An equation of the form or is solved by double integration: , , whence . Having integrated this function, we obtain a new function of f(x), which we denote by F(x). Thus, ; . Let's integrate again: or y=Ф(x). We obtained a general solution to the equation containing two arbitrary constants and .
Example 1. Solve the equation.
Solution:, , ,
Example 2. Solve the equation . Solution: , , .
SECTION 3.2. Number series, its members
Definition 1.Number series is called an expression of the form ++…++…, (1)
Where , , …, , … - numbers belonging to some specific number system.
Thus, we can talk about real series for which R, about complex series for which C, i= 1, 2, …, n, ... = =.
Section 3.3. Fundamentals of probability theory and mathematical statistics
4.1. SIMPLE INTEGRATION METHODS 4.1.1. The concept of an indefinite integral
In differential calculus, the problem of finding the derivative or differential with respect to a given function was considered y= F(x), i.e. it was necessary to find f(x)= F"(x) or dF(x)= F"(x)dx= f(x)dx. Let us pose the inverse problem: to restore the differentiated function, i.e., knowing the derivative f(x)(or differential f(x)dx), find such a function F(x), to F"(x)= f(x). This task turns out to be much more difficult than the task of differentiation. For example, let the speed of movement of a point be known, but we need to find the law
her movements S= S(t), and  To solve such
To solve such
tasks, new concepts and actions are introduced.
Definition. Differentiable function F(x) called antiderivative for function f(x) on (a; b), If F"(x)= f(x) on (a; b).
For example, for f(x) = x 2 antiderivative  because
because
 For f(x) = cos x the antiderivative will be F(x) = sin x, because F"(x) = (sin x)" = cos x, which coincides with f(x).
For f(x) = cos x the antiderivative will be F(x) = sin x, because F"(x) = (sin x)" = cos x, which coincides with f(x).
Does an antiderivative always exist for a given function? f(x)? Yes, if this function is continuous on (a; b). In addition, there are countless numbers of primitives, and they differ from each other only by a constant term. Indeed, sin x+ 2, sin x- 2, sin x+ c- all these functions will be antiderivatives for cos x(the derivative of a constant value is 0) - fig. 4.1.
Definition. Expression F(x)+ C, Where WITH- an arbitrary constant value that defines the set of antiderivatives for the function f(x), called indefinite integral and is indicated by the symbol  , i.e.
, i.e.  , where the sign is the sign of the indefinite
, where the sign is the sign of the indefinite
integral, f(x)- called integrand function, f (x)dx- by the integrand, x- integration variable.

Rice. 4.1. Example of a family of integral curves
Definition. The operation of finding an antiderivative from a given derivative or differential is called integration this function.
Integration is the inverse action of differentiation; it can be verified by differentiation, and differentiation is unique, and integration gives the answer up to a constant. Giving a constant value WITH specific values  By-
By-
We get various functions
each of which defines a curve on the coordinate plane called integral. All graphs of integral curves are shifted parallel to each other along the axis Oy. Therefore, a geometrically indefinite integral is a family of integral curves.
So, new concepts (antiderivative and indefinite integral) and a new action (integration) have been introduced, but how do you still find the antiderivative? To easily answer this question, you must first compile and memorize a table of indefinite integrals of basic elementary functions. It is obtained by inverting the corresponding differentiation formulas. For example, if
Typically, the table includes some integrals obtained after applying the simplest integration methods. These formulas are marked in the table. 4.1 with the symbol “*” and are proven in the further presentation of the material.
Table 4.1. Table of basic indefinite integrals

Formula 11 from table. 4.1 may look like  ,
,
because. A similar remark about the form
mules 13: 

4.1.2. Properties of indefinite integrals
Let's consider the simplest properties of the indefinite integral, which will allow us to integrate not only the basic elementary functions.
1. The derivative of the indefinite integral is equal to the integrand:
2. The differential of the indefinite integral is equal to the integrand:
3. The indefinite integral of the differential of a function is equal to this function added to an arbitrary constant:
Example 1.  Example 2.
Example 2. 
4. The constant factor can be taken out of the integral sign: Example 3. 
5. The integral of the sum or difference of two functions is equal to the sum or difference of the integrals of these functions:
Example 4.
The integration formula remains valid if the integration variable is a function: if  That
That
An arbitrary function that has a continuous derivative. This property is called invariance.
Example 5.  , That's why
, That's why
Compare with 
There is no universal method of integration. Below we will present some methods that allow you to calculate a given integral using properties 1-5 and table. 4.1.
4.1.3.Direct integration
This method consists of direct use of table integrals and properties 4 and 5. Examples.

4.1.4.Decomposition method
This method consists of expanding the integrand into a linear combination of functions with already known integrals.
Examples.

4.1.5. Method of subscribing to the differential sign
To reduce this integral to a tabular one, it is convenient to make differential transformations.
1. Subsuming the differential sign of a linear function
 from here
from here  in particular, dx =
d(x
+
b),
in particular, dx =
d(x
+
b),
 the differential does not change if you add to the variable
the differential does not change if you add to the variable
or subtract a constant value. If the variable increases several times, then the differential is multiplied by its reciprocal value. Examples with solutions.


Let's check formulas 9*, 12* and 14* from the table. 4.1, using the method of subscribing to the differential sign:

Q.E.D.
2. Subsuming the basic elementary functions under the differential sign:



Comment. Formulas 15* and 16* can be verified by differentiation (see property 1). For example,

and this is the integrand function from formula 16*.
4.1.6. Method for separating a perfect square from a quadratic trinomial
When integrating expressions like  or
or
 separating a perfect square from a quadratic trinomial
separating a perfect square from a quadratic trinomial
ax 2 + bx+ c it is possible to reduce them to tabular 12*, 14*, 15* or 16* (see Table 4.1).
Since in general this operation looks more complicated than it actually is, we will limit ourselves to examples.
Examples.
1.
Solution. Here we extract the perfect square from the quadratic trinomial x 2 + 6x+ 9 = (x 2 + 6x+ 9) - 9 + 5 = (x+ 3) 2 - 4, and then we use the method of subsuming the differential sign.
Using similar reasoning, we can calculate the following integrals:
2. 3.

At the final stage of integration, formula 16* was used.
4.1.7. Basic integration methods
There are two such methods: the method of changing a variable, or substitution, and integration by parts.
Variable Replacement Method
There are two formulas for changing a variable in an indefinite integral:
1) 2)
Here, the essence is monotone differentiable functions
tions of their variables.
The art of applying the method consists mainly in choosing functions so that the new integrals are tabular or reduce to them. The final answer should return to the old variable.
Note that substitution under the differential sign is a special case of variable replacement.
Examples.

Solution.A new variable should be entered heretso as to get rid of the square root. Let's putx+ 1 = t, Then x= t 2+ 1, and dx = 2 tdt:

Solution. Replacing x- 2 per t, we obtain a monomial in the denominator and after term-by-term division the integral is reduced to the tabular integral of the power function:



When passing to a variable x formulas used:
Method of integration by parts
The differential of the product of two functions is determined by the formula
Integrating this equality (see property 3), we find:

From here  This is the formula integration by
This is the formula integration by
parts.
Integration by parts involves the subjective representation of the integrand in the form u
. dV, and at the same time the integral  should be easier than
should be easier than  Otherwise application
Otherwise application
the method doesn't make sense.
So, the method of integration by parts assumes the ability to isolate factors from the integrand u And dV taking into account the above requirements.
We present a number of typical integrals that can be found by the method of integration by parts. 1. Integrals of the form
Where P(x)- polynomial; k- constant. In this case u= P(x), and dV- all other factors.
Example 1.

2.Integrals of type
Here we put other factors.
Example 2.

Example 3.  Example 4.
Example 4.

Any result can be verified by differentiation. For example, in this case
The result is correct.
3.Integrals of the form
where a, b- const. Behind u should take e ax , sin bx or cos bx.
Example 5.

From here we get Example 6.

From here

Example 7.  Example 8.
Example 8. 
Solution.Here you need to first make a change of variable, and then integrate by parts:
Example 9.  Example 10.
Example 10. 
Solution. This integral can be found with equal success either by replacing the variable 1 + x 2 = t 2 or by integrating by parts:

Independent work
Perform direct integration (1-10).

Apply simple integration methods (11-46).



Perform integration using change of variable and integration by parts methods (47-74).



 Mikhail Lermontov poem “Motherland” (I love my fatherland, but with a strange love!
Mikhail Lermontov poem “Motherland” (I love my fatherland, but with a strange love!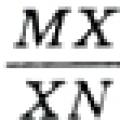 Review Questions for Chapter VI
Review Questions for Chapter VI Topics: Natural resources of the Far East Protection of water resources of the country and our region
Topics: Natural resources of the Far East Protection of water resources of the country and our region