Simplified multiplication formulas. Abbreviated multiplication formulas with examples
Abbreviated multiplication formulas.
Studying abbreviated multiplication formulas: the square of the sum and the square of the difference of two expressions; difference of squares of two expressions; cube of the sum and cube of the difference of two expressions; sums and differences of cubes of two expressions.
Application of abbreviated multiplication formulas when solving examples.
To simplify expressions, factor polynomials, and reduce polynomials to standard form, abbreviated multiplication formulas are used. Abbreviated multiplication formulas need to be known by heart.
Let a, b R. Then:
1. The square of the sum of two expressions is equal to the square of the first expression plus twice the product of the first expression and the second plus the square of the second expression.
(a + b) 2 = a 2 + 2ab + b 2
2. The square of the difference of two expressions is equal to the square of the first expression minus twice the product of the first expression and the second plus the square of the second expression.
(a - b) 2 = a 2 - 2ab + b 2
3. Difference of squares two expressions is equal to the product of the difference of these expressions and their sum.
a 2 - b 2 = (a -b) (a+b)
4. Cube of sum two expressions is equal to the cube of the first expression plus triple the product of the square of the first expression and the second plus triple the product of the first expression and the square of the second plus the cube of the second expression.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Difference cube two expressions is equal to the cube of the first expression minus triple the product of the square of the first expression and the second plus triple the product of the first expression and the square of the second minus the cube of the second expression.
(a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3
6. Sum of cubes two expressions is equal to the product of the sum of the first and second expressions and the incomplete square of the difference of these expressions.
a 3 + b 3 = (a + b) (a 2 - ab + b 2)
7. Difference of cubes two expressions is equal to the product of the difference of the first and second expressions by the incomplete square of the sum of these expressions.
a 3 - b 3 = (a - b) (a 2 + ab + b 2)
Application of abbreviated multiplication formulas when solving examples.
Example 1.
Calculate
a) Using the formula for the square of the sum of two expressions, we have
(40+1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681
b) Using the formula for the square of the difference of two expressions, we obtain
98 2 = (100 – 2) 2 = 100 2 - 2 100 2 + 2 2 = 10000 – 400 + 4 = 9604
Example 2.
Calculate
Using the formula for the difference of the squares of two expressions, we get
Example 3.
Simplify an expression
(x - y) 2 + (x + y) 2
Let's use the formulas for the square of the sum and the square of the difference of two expressions
(x - y) 2 + (x + y) 2 = x 2 - 2xy + y 2 + x 2 + 2xy + y 2 = 2x 2 + 2y 2
Abbreviated multiplication formulas in one table:
(a + b) 2 = a 2 + 2ab + b 2
(a - b) 2 = a 2 - 2ab + b 2
a 2 - b 2 = (a - b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3
a 3 + b 3 = (a + b) (a 2 - ab + b 2)
a 3 - b 3 = (a - b) (a 2 + ab + b 2)
When, etc. Below we will look at the most popular formulas and analyze how they are obtained.
Square of the sum
Let us square the sum of two monomials, like this: \((a+b)^2\). Squaring is the multiplication of a number or expression by itself, that is, \((a+b)^2=(a+b)(a+b)\). Now we can simply open the brackets, multiplying them as we did, and bring similar terms. We get:
And if we omit the intermediate calculations and write only the initial and final expressions, we get the final formula:
Squared sum:\((a+b)^2=a^2+2ab+b^2\)
Most students learn it by heart. And now you know how to derive this formula, and if you suddenly forget, you can always do it.
Okay, but how to use it and why is this formula needed? The square of the sum allows you to quickly write the result of squaring the sum of two terms. Let's look at an example.
Example
. Expand brackets: \((x+5)^2\)
Solution
:

Notice how much faster and with less effort the result was obtained in the second case. And when you master this and other formulas to the point of automatism, it will be even faster: you can simply write the answer right away. That's why they are called REDUCED multiplication formulas. So, knowing them and learning to apply them is definitely worth it.
Just in case, we note that as \(a\) And \(b\) There can be any expressions - the principle remains the same. For example:

If you suddenly do not understand some transformations in the last two examples, repeat the topic.
Example . Convert the expression \((1+5x)^2-12x-1 \) to standard form.
Solution :
Answer: \(25x^2-2x\).
Important! It is necessary to learn to use formulas not only in the “forward” direction, but also in the “reverse” direction.
Example . Calculate the value of the expression \((368)^2+2·368·132+(132)^2\) without a calculator.
Solution :
Answer: \(250 000\).
Squared difference
Above we found the formula for the sum of monomials. Let's now find the formula for the difference, that is, for \((a-b)^2\):
In a more concise form we have:
Squared difference: \((a-b)^2=a^2-2ab+b^2\)
It is used in the same way as the previous one.
Example . Simplify the expression \((2a-3)^2-4(a^2-a)\) and find its value at \(a=\frac(17)(8)\).
Solution :
Answer: \(8\).
Difference of squares
So, we have dealt with the situations of the product of two brackets with a plus in them and two brackets with a minus. The remaining case is the product of identical parentheses with different signs. Let's see what happens:
We got the formula:
Difference of squares \(a^2-b^2=(a+b)(a-b)\)
This formula is one of the most frequently used when working with.
Example . Reduce the fraction \(\frac(x^2-9)(x-3)\) .
Solution :
Answer: \(x+3\).
Example
.Factorize \(25x^4-m^(10) t^6\).
Solution
:
These are the three basic formulas you need to know Necessarily! There are also formulas with cubes (see above), it is also advisable to remember them or be able to quickly derive them. Let us also note that in practice, several such formulas are often encountered in one problem at once - this is normal. Just learn to notice the formulas and apply them carefully, and everything will be fine.
Example (advanced!)
.Reduce the fraction.
Solution
:
|
\(\frac(x^2-4xy-9+4y^2)(x-2y+3)\)\(=\) |
At first glance, this is a quiet horror and nothing can be done about it (we are not seriously considering the “lie down and die” option). |
|
|
\(\frac((x^2-4xy+4y^2)-9)(x-2y+3)\)\(=\) |
Now let’s transform the terms in the bracket a little: |
|
|
\(\frac((x^2-4xy+(2y)^2)-9)(x-2y+3)\)\(=\) |
Now let’s take a closer look and notice that in the bracket we have a formula for the squared difference, which has \(a=x\), \(b=2y\). We collapse along it to the form of brackets in a square. And at the same time we represent nine as \(3\) squared. |
|
|
\(\frac((x-2y)^2-3^2)(x-2y+3)\)\(=\) |
Once again we carefully look at the numerator... think... think... and notice the formula for the difference of squares, which has \(a=(x-2y)\), \(b=3\). We decompose it to the product of two brackets. |
|
|
\(\frac((x-2y-3)(x-2y+3))(x-2y+3)\)\(=\) |
And now we reduce the second bracket of the numerator and the entire denominator. |
|
|
The answer is ready. |
Square of the sum of two expressions
There are a number of cases where multiplying a polynomial by a polynomial can be greatly simplified. For example, this is the case (2 x+ 3y) 2 .
Expression (2 x+ 3y) 2 is the multiplication of two polynomials, each of which is equal to (2 x+ 3y)
(2x+ 3y) 2 = (2x+ 3y)(2x+ 3y)
We obtained the multiplication of a polynomial by a polynomial. Let's execute it:
(2x+ 3y) 2 = (2x+ 3y)(2x+ 3y) = 4x 2 + 6xy + 6xy + 9y 2 = 4x 2 + 12xy+ 9y 2
That is, the expression (2 x+ 3y) 2 equals 4x 2 + 12xy + 9y 2
(2x+ 3y) 2 = 4x 2 + 12xy+ 9y 2
Let's solve a similar example, which is simpler:
(a+b) 2
Expression ( a+b) 2 is the multiplication of two polynomials, each of which is equal to ( a+b)
(a+b) 2 = (a+b)(a+b)
Let's do this multiplication:
(a+b) 2 = (a+b)(a+b) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2
That is, the expression (a+b) 2 equals a 2 + 2ab + b 2
(a+b) 2 = a 2 + 2ab + b 2
It turns out that the case ( a+b) 2 can be extended to any a And b. The first example we solved, namely (2 x+ 3y) 2 can be solved using the identity (a+b) 2 = a 2 + 2ab + b 2 . To do this, you need to substitute instead of variables a And b corresponding terms from expression (2 x+ 3y) 2 . In this case, the variable a corresponds to member 2 x, and the variable b corresponds to member 3 y
a = 2x
b = 3y
And then we can use the identity (a+b) 2 = a 2 + 2ab + b 2 , but instead of variables a And b you need to substitute expressions 2 x and 3 y respectively:
(2x+ 3y) 2 = (2x) 2 + 2 × 2 x× 3 y + (3y) 2 = 4x 2 + 12xy+ 9y 2
Just like last time we got a polynomial 4x 2 + 12xy+ 9y 2 . The solution is usually written down briefly, performing all the elementary transformations in the mind:
(2x+ 3y) 2 = 4x 2 + 12xy+ 9y 2
Identity (a+b) 2 = a 2 + 2ab + b 2 called the formula for the square of the sum of two expressions. This formula can be read like this:
The square of the sum of two expressions is equal to the square of the first expression plus twice the product of the first expression and the second plus the square of the second expression.
Consider the expression (2 + 3) 2. It can be calculated in two ways: perform addition in parentheses and square the resulting result, or use the formula for the square of the sum of two expressions.
First way:
(2 + 3) 2 = 5 2 = 25
Second way:
(2 + 3) 2 = 2 2 + 2 × 2 × 3 + 3 2 = 4 + 12 + 9 = 25
Example 2. Convert Expression (5 a+ 3) 2 into a polynomial.
Let's use the formula for the square of the sum of two expressions:
(a+b) 2 = a 2 + 2ab + b 2
(5a+ 3) 2 = (5a) 2 + 2 × 5 a × 3 + 3 2 = 25a 2 + 30a + 9
Means, (5a+ 3) 2 = 25a 2 + 30a + 9.
Let's try to solve this example without using the square of the sum formula. We should get the same result:
(5a+ 3) 2 = (5a+ 3)(5a+ 3) = 25a 2 + 15a + 15a + 9 = 25a 2 + 30a + 9
The formula for the square of the sum of two expressions has a geometric meaning. We remember that to calculate the area of a square we need to raise its side to the second power.
For example, the area of a square with side a will be equal a 2. If you increase the side of a square by b, then the area will be equal to ( a+b) 2
Consider the following figure:
Let's imagine that the side of the square shown in this figure is increased by b. A square has all sides equal. If its side is increased by b, then the remaining sides will also increase by b

The result is a new square, which is larger than the previous one. To see it clearly, let’s complete the missing sides:

To calculate the area of this square, you can separately calculate the squares and rectangles included in it, then add the results.
First you can calculate a square with side a- its area will be equal a 2. Then you can calculate rectangles with sides a And b- they will be equal ab. Then you can calculate the square with side b

The result is the following sum of areas:
a 2 + ab+ab + b 2
The sum of the areas of identical rectangles can be replaced by multiplying 2 ab, which will literally mean “repeat area of rectangle ab twice” . Algebraically, this is obtained by bringing similar terms ab And ab. The result is the expression a 2 + 2ab+ b 2 , which is the right side of the formula for the square of the sum of two expressions:
(a+b) 2 = a 2 + 2ab+ b 2
Square of the difference of two expressions
The formula for the squared difference of two expressions is as follows:
(a − b) 2 = a 2 − 2ab + b 2
The square of the difference of two expressions is equal to the square of the first expression minus twice the product of the first expression and the second plus the square of the second expression.
The formula for the square of the difference of two expressions is derived in the same way as the formula for the square of the sum of two expressions. Expression ( a − b) 2 is the product of two polynomials, each of which is equal to ( a − b)
(a − b) 2 = (a − b)(a − b)
If you perform this multiplication, you get a polynomial a 2 − 2ab + b 2
(a − b) 2 = (a − b)(a − b) = a 2 − ab− ab+ b 2 = a 2 − 2ab + b 2
Example 1. Convert Expression (7 x− 5) 2 into a polynomial.
Let's use the formula for the square of the difference of two expressions:
(a − b) 2 = a 2 − 2ab + b 2
(7x− 5) 2 = (7x) 2 − 2 × 7 x × 5 + 5 2 = 49x 2 − 70x + 25
Means, (7x− 5) 2 = 49x 2 + 70x + 25.
Let's try to solve this example without using the squared difference formula. We should get the same result:
(7x− 5) 2 = (7x− 5) (7x− 5) = 49x 2 − 35x − 35x + 25 = 49x 2 − 70x+ 25.
The formula for the square of the difference of two expressions also has a geometric meaning. If the area of a square with side a equal to a 2, then the area of a square whose side is reduced by b, will be equal to ( a − b) 2
Consider the following figure:

Let's imagine that the side of the square shown in this figure is reduced by b. A square has all sides equal. If one side is reduced by b, then the remaining sides will also decrease by b

The result is a new square, which is smaller than the previous one. It is highlighted in yellow in the figure. Its side is equal a− b because the old side a decreased by b. To calculate the area of this square, you can from the original area of the square a 2 subtract the areas of the rectangles that were obtained in the process of reducing the sides of the old square. Let's show these rectangles:

Then you can write the following expression: old square a 2 minus area ab minus area ( a − b)b
a 2 − ab − (a − b)b
Let's expand the parentheses in the expression ( a − b)b
a 2 − ab−ab + b 2
Let's look at similar terms:
a 2 − 2ab + b 2
The result is the expression a 2 − 2ab + b 2 , which is the right side of the formula for the square of the difference of two expressions:
(a − b) 2 = a 2 − 2ab + b 2
The squared sum and squared difference formulas are generally called abbreviated multiplication formulas. These formulas can significantly simplify and speed up the process of multiplying polynomials.
Earlier we said that when considering a member of a polynomial separately, it must be considered together with the sign that is located in front of it.
But when using abbreviated multiplication formulas, the sign of the original polynomial should not be considered as the sign of this term itself.
For example, if given the expression (5 x − 2y) 2 and we want to use the formula (a − b) 2 = a 2 − 2ab + b 2 , then instead b need to substitute 2 y, not −2 y. This is a feature of working with formulas that should not be forgotten.
(5x − 2y) 2
a = 5x
b = 2y
(5x − 2y) 2 = (5x) 2 − 2 × 5 x× 2 y + (2y) 2 = 25x 2 − 20xy + 4y 2
If we substitute −2 y, then this will mean that the difference in the parentheses of the original expression has been replaced by the sum:
(5x − 2y) 2 = (5x + (−2y)) 2
and in this case, you need to use not the squared difference formula, but the squared sum formula:
(5x + (−2y) 2
a = 5x
b = −2y
(5x + (−2y)) 2 = (5x) 2 + 2 × 5 x× (−2 y) + (−2y) 2 = 25x 2 − 20xy + 4y 2
An exception may be expressions of the form (x− (−y)) 2 . In this case, using the formula (a − b) 2 = a 2 − 2ab + b 2 instead of b should be substituted (− y)
(x− (−y)) 2 = x 2 − 2 × x× (− y) + (−y) 2 = x 2 + 2xy + y 2
But squaring expressions of the form x − (−y), it will be more convenient to replace subtraction with addition x+y. Then the original expression will take the form ( x+y) 2 and it will be possible to use the formula for the square of the sum, rather than the difference:
(x+y) 2 = x 2 + 2xy + y 2
Cube of sum and cube of difference
The formulas for the cube of the sum of two expressions and the cube of the difference of two expressions are as follows:
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3
The formula for the cube of the sum of two expressions can be read as follows:
The cube of the sum of two expressions is equal to the cube of the first expression plus triple the product of the square of the first expression and the second plus triple the product of the first expression and the square of the second plus the cube of the second expression.
And the formula for the cube of the difference between two expressions can be read as follows:
The cube of the difference of two expressions is equal to the cube of the first expression minus triple the product of the square of the first expression and the second plus triple the product of the first expression and the square of the second minus the cube of the second expression.
When solving problems, it is advisable to know these formulas by heart. If you don’t remember, no problem! You can remove them yourself. We already know how to do this.
Let us derive the formula for the cube of the sum ourselves:
(a+b) 3
Expression ( a+b) 3 is the product of three polynomials, each of which is equal to ( a+ b)
(a+b) 3 = (a+ b)(a+ b)(a+ b)
But the expression ( a+b) 3 can also be written as (a+ b)(a+ b) 2
(a+b) 3 = (a+ b)(a+ b) 2
In this case, the factor ( a+ b) 2 is the square of the sum of the two expressions. This square of the sum is equal to the expression a 2 + 2ab + b 2 .
Then ( a+b) 3 can be written as (a+ b)(a 2 + 2ab + b 2) .
(a+b) 3 = (a+ b)(a 2 + 2ab + b 2)
And this is multiplying a polynomial by a polynomial. Let's execute it:
(a+b) 3 = (a+ b)(a 2 + 2ab + b 2) = a 3 + 2a 2 b + ab 2 + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Similarly, you can derive the formula for the cube of the difference of two expressions:
(a − b) 3 = (a − b)(a 2 − 2ab + b 2) = a 3 − 2a 2 b + ab 2 − a 2 b + 2ab 2 − b 3 = a 3 − 3a 2 b+ 3ab 2 − b 3
Example 1. Transform the expression ( x+ 1) 3 into a polynomial.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(x+ 1) 3 = x 3+3× x 2 × 1 + 3 × x× 1 2 + 1 3 = x 3 + 3x 2 + 3x + 1
Let's try to solve this example without using the formula for the cube of the sum of two expressions
(x+ 1) 3 = (x+ 1)(x+ 1)(x+ 1) = (x+ 1)(x 2 + 2x + 1) = x 3 + 2x 2 + x + x 2 + 2x + 1 = x 3 + 3x 2 + 3x + 1
Example 2. Convert Expression (6a 2 + 3b 3) 3 into a polynomial.
Let's use the formula for the cube of the sum of two expressions:
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(6a 2 + 3b 3) 3 = (6a 2) 3 + 3 × (6 a 2) 2×3 b 3 + 3 × 6 a 2 × (3b 3) 2 + (3b 3) 3 = 216a 6 + 3 × 36 a 4×3 b 3 + 3 × 6 a 2×9 b 6 + 27b 9
Example 3. Convert Expression ( n 2 − 3) 3 into a polynomial.
(a − b) = a 3 − 3a 2 b + 3ab 2 − b 3
(n 2 − 3) 3 = (n 2) 3 − 3 × ( n 2) 2 × 3 + 3 × n 2 × 3 2 − 3 3 = n 6 − 9n 4 + 27n 2 − 27
Example 4. Convert Expression (2x 2 − x 3) 3 into a polynomial.
Let's use the formula for the cube of the difference of two expressions:
(a − b) = a 3 − 3a 2 b + 3ab 2 − b 3
(2x 2 − x 3) 3 = (2x 2) 3 − 3 × (2 x 2) 2× x 3 + 3 × 2 x 2×( x 3) 2 − (x 3) 3 =
8x 6 − 3 × 4 x 4× x 3 + 3 × 2 x 2× x 6 − x 9 =
8x 6 − 12x 7 + 6x 8 − x 9
Multiplying the difference of two expressions by their sum
There are problems in which you need to multiply the difference of two expressions by their sum. For example:
(a − b)(a+b)
In this expression, the difference of two expressions a And b multiplied by the sum of the same two expressions. Let's do this multiplication:
(a − b)(a+b) = a 2 + ab − ab − b 2 = a 2 − b 2
That is, the expression (a − b)(a+b) equals a 2 − b 2
(a − b)(a+b) = a 2 − b 2
We see that when we multiply the difference of two expressions by their sum, we get the difference of the squares of these expressions.
The product of the difference of two expressions and their sum is equal to the difference of the squares of these expressions.
Happening (a − b)(a+b) can be distributed to anyone a And b. Simply put, if when solving a problem you need to multiply the difference of two expressions by their sum, then this multiplication can be replaced by the difference of the squares of these expressions.
Example 1. Perform multiplication (2x − 5)(2x + 5)
In this example, the difference of expressions is 2 x and 5 multiplied by the sum of the same expressions. Then according to the formula (a − b)(a+b) = a 2 − b 2 we have:
(2x − 5)(2x + 5) = (2x) 2 − 5 2
Let's calculate the right side, we get 4 x 2 − 25
(2x − 5)(2x + 5) = (2x) 2 − 5 2 = 4x 2 − 25
Let's try to solve this example without using the formula (a − b)(a+b) = a 2 − b 2 . We will get the same result 4 x 2 − 25
(2x − 5)(2x + 5) = 4x 2 − 10x + 10x − 25 = 4x 2 − 25
Example 2. Perform multiplication (4x − 5y)(4x + 5y)
(a − b)(a+b) = a 2 − b 2
(4x − 5y)(4x + 5y) = (4x) 2 − (5y) 2 = 16x 2 − 25y 2
Example 3. Perform multiplication (2a+ 3b)(2a− 3b)
Let's use the formula for multiplying the difference of two expressions by their sum:
(a − b)(a+b) = a 2 − b 2
(2a+ 3b)(2a − 3b) = (2a) 2 − (3b) 2 = 4a 2 − 9b 2
In this example, the sum of the terms is 2 a and 3 b was located earlier than the difference of these terms. And in the formula (a − b)(a+b) = a 2 − b 2 the difference is located earlier.
It makes no difference how the factors are arranged ( a − b) V ( a+b) in the formula. They can be written as (a − b)(a+b) , so (a+b)(a − b) . The result will still be equal a 2 − b 2, since the product does not change from rearranging the factors.
So in this example, the factors (2 a+ 3b) and 2 a − 3b) can be written as (2a+ 3b)(2a − 3b) , so (2a − 3b)(2a+ 3b) . The result will still be 4 a 2 − 9b 2 .
Example 3. Perform multiplication (7 + 3x)(3x − 7)
Let's use the formula for multiplying the difference of two expressions by their sum:
(a − b)(a+b) = a 2 − b 2
(7 + 3x)(3x − 7) = (3x) 2 − 7 2 = 9x 2 − 49
Example 4. Perform multiplication (x 2 − y 3)(x 2 + y 3)
(a − b)(a+b) = a 2 − b 2
(x 2 − y 3)(x 2 + y 3) = (x 2) 2 − (y 3) 2 = x 4 − y 6
Example 5. Perform multiplication (−5x− 3y)(5x− 3y)
In the expression (−5 x− 3y) we put −1 out of brackets, then the original expression will take the following form:
(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y)
Work (5x + 3y)(5x − 3y) replace it with the difference of squares:
(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y) = −1((5x) 2 − (3y) 2)
The difference of squares was enclosed in parentheses. If this is not done, then it turns out that −1 is only multiplied by (5 x) 2 . And this will lead to an error and a change in the value of the original expression.
(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y) = −1((5x) 2 − (3y) 2) = −1(25x 2 − 9x 2)
Now multiply −1 by the expression in brackets and get the final result:
(−5x− 3y)(5x− 3y) = −1(5x + 3y)(5x − 3y) = −1((5x) 2 − (3y) 2) =
−1(25x 2 − 9y 2) = −25x 2 + 9y 2
Multiplying the difference of two expressions by the partial square of their sum
There are problems in which you need to multiply the difference of two expressions by the partial square of their sum. This piece looks like this:
(a − b)(a 2 + ab + b 2)
The first polynomial ( a − b) is the difference of two expressions, and the second is a polynomial (a 2 + ab + b 2) is the partial square of the sum of these two expressions.
The partial square of the sum is a polynomial of the form a 2 + ab + b 2 . It is similar to the usual square of the sum a 2 + 2ab + b 2
For example, the expression 4x 2 + 6xy + 9y 2 is the incomplete square of the sum of expressions 2 x and 3 y .
Indeed, the first term of the expression 4x 2 + 6xy + 9y 2 , namely 4 x 2 is the square of expression 2 x, since (2 x) 2 = 4x 2. Third term of expression 4x 2 + 6xy + 9y 2 , namely 9 y 2 is the square of expression 3 y, since (3 y) 2 = 9y 2. Member in the middle 6 xy, is the product of expressions 2 x and 3 y.
So, let's multiply the difference ( a − b) by the incomplete square of the sum a 2 + ab + b 2
(a − b)(a 2 + ab + b 2) = a(a 2 + ab + b 2) − b(a 2 + ab + b 2) =
a 3 + a 2 b + ab 2 − a 2 b − ab 2 − b 3 = a 3 − b 3
That is, the expression (a − b)(a 2 + ab + b 2) equals a 3 − b 3
(a − b)(a 2 + ab + b 2) = a 3 − b 3
This identity is called the formula for multiplying the difference of two expressions by the partial square of their sum. This formula can be read like this:
The product of the difference of two expressions and the partial square of their sum is equal to the difference of the cubes of these expressions.
Example 1. Perform multiplication (2x − 3y)(4x 2 + 6xy + 9y 2)
First polynomial (2 x − 3y) is the difference of two expressions 2 x and 3 y. Second polynomial 4x 2 + 6xy + 9y 2 this is the partial square of the sum of two expressions 2 x and 3 y. This allows you to use the formula without making long calculations (a − b)(a 2 + ab + b 2) = a 3 − b 3 . In our case, multiplication (2x − 3y)(4x 2 + 6xy + 9y 2) can be replaced by difference of cubes 2 x and 3 y
(2x − 3y)(4x 2 + 6xy + 9y 2) = (2x) 3 − (3y) 3 = 8x 3 − 27y 3
(a − b)(a 2 + ab+ b 2) = a 3 − b 3 . We will get the same result, but the solution will be longer:
(2x − 3y)(4x 2 + 6xy + 9y 2) = 2x(4x 2 + 6xy + 9y 2) − 3y(4x 2 + 6xy + 9y 2) =
8x 3 + 12x 2 y + 18xy 2 − 12x 2 y − 18xy 2 − 27y 3 = 8x 3 − 27y 3
Example 2. Perform multiplication (3 − x)(9 + 3x + x 2)
The first polynomial (3 − x) is the difference of two expressions, and the second polynomial is the partial square of the sum of these two expressions. This allows us to use the formula (a − b)(a 2 + ab + b 2) = a 3 − b 3
(3 − x)(9 + 3x + x 2) = 3 3 − x 3 = 27 − x 3
Multiplying the sum of two expressions by the partial square of their difference
There are problems in which you need to multiply the sum of two expressions by the partial square of their difference. This piece looks like this:
(a+b)(a 2 − ab + b 2)
The first polynomial ( a+b (a 2 − ab + b 2) is the incomplete square of the difference of these two expressions.
The partial square of the difference is a polynomial of the form a 2 − ab + b 2 . It looks like a regular difference square a 2 − 2ab + b 2 except that in it the product of the first and second expressions is not doubled.
For example, the expression 4x 2 − 6xy + 9y 2 is the incomplete square of the difference of the expressions 2 x and 3 y.
(2x) 2 − 2x× 3 y + (3y) 2 = 4x 2 − 6xy + 9y 2
Let's return to the original example. Let's multiply the sum a+b by the partial square of the difference a 2 − ab + b 2
(a+b)(a 2 − ab + b 2) = a(a 2 − ab + b 2) + b(a 2 − ab + b 2) =
a 3 − a 2 b + ab 2 + a 2 b − ab 2 + b 3 = a 3 + b 3
That is, the expression (a+b)(a 2 − ab + b 2) equals a 3 + b 3
(a+b)(a 2 − ab + b 2) = a 3 + b 3
This identity is called the formula for multiplying the sum of two expressions by the incomplete square of their difference. This formula can be read like this:
The product of the sum of two expressions and the partial square of their difference is equal to the sum of the cubes of these expressions.
Example 1. Perform multiplication (2x + 3y)(4x 2 − 6xy + 9y 2)
First polynomial (2 x + 3y) is the sum of two expressions 2 x and 3 y, and the second polynomial 4x 2 − 6xy + 9y 2 this is the incomplete square of the difference of these expressions. This allows you to use the formula without making long calculations (a+b)(a 2 − ab + b 2) = a 3 + b 3 . In our case, multiplication (2x + 3y)(4x 2 − 6xy + 9y 2) can be replaced by the sum of cubes 2 x and 3 y
(2x + 3y)(4x 2 − 6xy + 9y 2) = (2x) 3 + (3y) 3 = 8x 3 + 27y 3
Let's try to solve the same example without using the formula (a+b)(a 2 − ab+ b 2) = a 3 + b 3 . We will get the same result, but the solution will be longer:
(2x + 3y)(4x 2 − 6xy + 9y 2) = 2x(4x 2 − 6xy + 9y 2) + 3y(4x 2 − 6xy + 9y 2) =
8x 3 − 12x 2 y + 18xy 2 + 12x 2 y − 18xy 2 + 27y 3 = 8x 3 + 27y 3
Example 2. Perform multiplication (2x+ y)(4x 2 − 2xy + y 2)
First polynomial (2 x+ y) is the sum of two expressions, and the second polynomial (4x 2 − 2xy + y 2) is the incomplete square of the difference of these expressions. This allows us to use the formula (a+b)(a 2 − ab+ b 2) = a 3 + b 3
(2x+ y)(4x 2 − 2xy + y 2) = (2x) 3 + y 3 = 8x 3 + y 3
Let's try to solve the same example without using the formula (a+b)(a 2 − ab+ b 2) = a 3 + b 3 . We will get the same result, but the solution will be longer:
(2x+ y)(4x 2 − 2xy + y 2) = 2x(4x 2 − 2xy + y 2) + y(4x 2 − 2xy + y 2) =
8x 3 − 4x 2 y + 2xy 2 + 4x 2 y − 2xy 2 + y 3 = 8x 3 + y 3
Tasks for independent solution
Did you like the lesson?
Join our new group VKontakte and start receiving notifications about new lessons
Abbreviated multiplication formulas (FMF) are used to exponentiate and multiply numbers and expressions. Often these formulas allow you to make calculations more compactly and quickly.
In this article we will list the basic formulas for abbreviated multiplication, group them in a table, consider examples of using these formulas, and also dwell on the principles of proof of formulas for abbreviated multiplication.
For the first time, the topic of FSU is considered within the framework of the Algebra course for the 7th grade. Below are 7 basic formulas.
Abbreviated multiplication formulas
- formula for the square of the sum: a + b 2 = a 2 + 2 a b + b 2
- square difference formula: a - b 2 = a 2 - 2 a b + b 2
- sum cube formula: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
- difference cube formula: a - b 3 = a 3 - 3 a 2 b + 3 a b 2 - b 3
- square difference formula: a 2 - b 2 = a - b a + b
- formula for sum of cubes: a 3 + b 3 = a + b a 2 - a b + b 2
- formula for difference of cubes: a 3 - b 3 = a - b a 2 + a b + b 2
The letters a, b, c in these expressions can be any numbers, variables or expressions. For ease of use, it is better to learn the seven basic formulas by heart. Let's put them in a table and present them below, encircling them with a frame.
The first four formulas allow you to calculate, respectively, the square or cube of the sum or difference of two expressions.
The fifth formula calculates the difference between the squares of expressions by multiplying their sum and difference.
The sixth and seventh formulas are, respectively, multiplying the sum and difference of expressions by the incomplete square of the difference and the incomplete square of the sum.
The abbreviated multiplication formula is sometimes also called the abbreviated multiplication identities. This is not surprising, since every equality is an identity.
When solving practical examples, abbreviated multiplication formulas with the left and right sides swapped are often used. This is especially convenient when factoring a polynomial.

Additional abbreviated multiplication formulas
Let's not limit ourselves to the 7th grade algebra course and add a few more formulas to our FSU table.
First, let's look at Newton's binomial formula.
a + b n = C n 0 · a n + C n 1 · a n - 1 · b + C n 2 · a n - 2 · b 2 + . . + C n n - 1 · a · b n - 1 + C n n · b n
Here C n k are the binomial coefficients that appear in line number n in Pascal’s triangle. Binomial coefficients are calculated using the formula:
C n k = n ! k! · (n - k) ! = n (n - 1) (n - 2) . . (n - (k - 1)) k !
As we can see, the FSF for the square and cube of the difference and the sum is a special case of the Newton binomial formula for n=2 and n=3, respectively.
But what if there are more than two terms in the sum that needs to be raised to a power? The formula for the square of the sum of three, four or more terms will be useful.
a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n - 1 a n
Another formula that may be useful is the formula for the difference between the nth powers of two terms.
a n - b n = a - b a n - 1 + a n - 2 b + a n - 3 b 2 + . . + a 2 b n - 2 + b n - 1
This formula is usually divided into two formulas - for even and odd powers, respectively.
For even 2m indicators:
a 2 m - b 2 m = a 2 - b 2 a 2 m - 2 + a 2 m - 4 b 2 + a 2 m - 6 b 4 + . . + b 2 m - 2
For odd exponents 2m+1:
a 2 m + 1 - b 2 m + 1 = a 2 - b 2 a 2 m + a 2 m - 1 b + a 2 m - 2 b 2 + . . + b 2 m
The difference of squares and difference of cubes formulas, as you guessed, are special cases of this formula for n = 2 and n = 3, respectively. For difference of cubes, b is also replaced by - b.
How to read abbreviated multiplication formulas?
We will give the appropriate formulations for each formula, but first we will understand the principle of reading formulas. The most convenient way to do this is with an example. Let's take the very first formula for the square of the sum of two numbers.
a + b 2 = a 2 + 2 a b + b 2 .
They say: the square of the sum of two expressions a and b is equal to the sum of the square of the first expression, twice the product of the expressions and the square of the second expression.
All other formulas are read similarly. For the square of the difference a - b 2 = a 2 - 2 a b + b 2 we write:
the square of the difference between two expressions a and b is equal to the sum of the squares of these expressions minus twice the product of the first and second expressions.
Let's read the formula a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3. The cube of the sum of two expressions a and b is equal to the sum of the cubes of these expressions, triple the product of the square of the first expression by the second, and triple the product of the square of the second expression by the first expression.
Let's move on to reading the formula for the difference of cubes a - b 3 = a 3 - 3 a 2 b + 3 a b 2 - b 3. The cube of the difference between two expressions a and b is equal to the cube of the first expression minus the triple product of the square of the first expression and the second, plus the triple product of the square of the second expression and the first expression, minus the cube of the second expression.
The fifth formula a 2 - b 2 = a - b a + b (difference of squares) reads like this: the difference of the squares of two expressions is equal to the product of the difference and the sum of the two expressions.
For convenience, expressions like a 2 + a b + b 2 and a 2 - a b + b 2 are called, respectively, the incomplete square of the sum and the incomplete square of the difference.
Taking this into account, the formulas for the sum and difference of cubes can be read as follows:
The sum of the cubes of two expressions is equal to the product of the sum of these expressions and the partial square of their difference.
The difference between the cubes of two expressions is equal to the product of the difference between these expressions and the partial square of their sum.
Proof of the FSU
Proving FSU is quite simple. Based on the properties of multiplication, we will multiply the parts of the formulas in brackets.
For example, consider the formula for the squared difference.
a - b 2 = a 2 - 2 a b + b 2 .
To raise an expression to the second power, you need to multiply this expression by itself.
a - b 2 = a - b a - b .
Let's expand the brackets:
a - b a - b = a 2 - a b - b a + b 2 = a 2 - 2 a b + b 2 .
The formula is proven. The remaining FSUs are proven similarly.
Examples of FSU application
The purpose of using abbreviated multiplication formulas is to quickly and concisely multiply and raise expressions to powers. However, this is not the entire scope of application of the FSU. They are widely used in reducing expressions, reducing fractions, and factoring polynomials. Let's give examples.
Example 1. FSU
Let's simplify the expression 9 y - (1 + 3 y) 2.
Let's apply the sum of squares formula and get:
9 y - (1 + 3 y) 2 = 9 y - (1 + 6 y + 9 y 2) = 9 y - 1 - 6 y - 9 y 2 = 3 y - 1 - 9 y 2
Example 2. FSU
Let's reduce the fraction 8 x 3 - z 6 4 x 2 - z 4.
We note that the expression in the numerator is the difference of cubes, and in the denominator is the difference of squares.
8 x 3 - z 6 4 x 2 - z 4 = 2 x - z (4 x 2 + 2 x z + z 4) 2 x - z 2 x + z .
We reduce and get:
8 x 3 - z 6 4 x 2 - z 4 = (4 x 2 + 2 x z + z 4) 2 x + z
FSUs also help calculate the values of expressions. The main thing is to be able to notice where to apply the formula. Let's show this with an example.
Let's square the number 79. Instead of cumbersome calculations, let's write:
79 = 80 - 1 ; 79 2 = 80 - 1 2 = 6400 - 160 + 1 = 6241 .
It would seem that, complex calculation carried out quickly just using abbreviated multiplication formulas and multiplication tables.
Another important point- identifying the square of the binomial. The expression 4 x 2 + 4 x - 3 can be converted into 2 x 2 + 2 · 2 · x · 1 + 1 2 - 4 = 2 x + 1 2 - 4 . Such transformations are widely used in integration.
If you notice an error in the text, please highlight it and press Ctrl+Enter
Multiplying a polynomial by a polynomial
! To multiply a polynomial by a polynomial, you need to multiply each term of one polynomial by each term of the other polynomial and add the resulting products.
Be careful! Each term has its own sign.
Abbreviated multiplication formulas Polynomials are generally 7 (seven) common cases of multiplying polynomials.
Definitions andAbbreviated multiplication formulas. Table
Table 2. Definitions of abbreviated multiplication formulas (click to enlarge)
Three abbreviated multiplication formulas for squares
1. Formula for squared sum.
Square of the sum two expressions is equal to the square of the first expression plus twice the product of the first expression and the second plus the square of the second expression.
To better understand the formula, let's first simplify the expression (expand the formula for the square of the sum)

Now let’s factorize (collapse the formula)

Sequence of actions when factoring:
- determine which monomials were squared ( 5 And 3m);
- check if their double product is in the middle of the formula (2 5 3m = 30m);
- write down the answer (5 + 3m) 2.
2. Square difference formula
Squared difference two expressions is equal to the square of the first expression minus twice the product of the first expression and the second plus the square of the second expression.
First, let's simplify the expression (expand the formula):

And then vice versa, let’s factorize it (collapse the formula):

3. Square difference formula
The product of the sum of two expressions and their difference is equal to the difference of the squares of these expressions.
Let's collapse the formula (perform multiplication)
Now let’s expand the formula (factor it)

Four abbreviated multiplication formulas for cubes
4. Formula for the cube of the sum of two numbers
The cube of the sum of two expressions is equal to the cube of the first expression plus triple the product of the square of the first expression and the second plus triple the product of the first expression and the square of the second plus the cube of the second expression.

The sequence of actions when “collapsing” the formula:
- find monomials that were cubed (here 4x And 1 );
- check the average terms for compliance with the formula;
- write down the answer.
5. Formula for the cube of the difference of two numbers
The cube of the difference of two expressions is equal to the cube of the first expression minus triple the product of the square of the first expression and the second plus triple the product of the first expression and the square of the second minus the cube of the second expression.

6. Formula for sum of cubes
The sum of the cubes of two expressions is equal to the product of the sum of the first and second expressions and the incomplete square of the difference of these expressions.

And back:

7. Difference of cubes formula
The difference between the cubes of two expressions is equal to the product of the difference between the first and second expressions and the partial square of the sum of these expressions.

Application of abbreviated multiplication formulas. Table
An example of using formulas in practice (oral calculation).
Task: Find the area of a square with side a = 71 cm.
Solution: S = a 2 . Using the squared sum formula, we have
71 2 = (70 + 1) 2 = 70 2 + 2*70*1 + 1 2 = 4900 + 140 + 1 = 5041 cm 2
Answer: 5041 cm 2
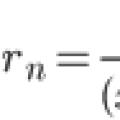 Taylor series expansion Approximate solution of the Cauchy problem for the ordinary
Taylor series expansion Approximate solution of the Cauchy problem for the ordinary What is NOT taught at school What is not taught at school ask
What is NOT taught at school What is not taught at school ask Money Thinking Formula (A
Money Thinking Formula (A