Chapter 3.

Basic theorems of probability theory and consequences from them

Theorem for adding incompatible probabilities

Events

The second chapter showed how the probability of a particular random event can be determined when certain conditions are met. As you know, with random events you can carry out arithmetic operations, the main ones being addition and multiplication events. Probability theory allows, using its basic theorems, to find the probability of the sum and product of events, i.e. determine either the probability of the occurrence of at least one of the events under consideration, or the probability of the simultaneous occurrence of these events.

The main theorems of probability theory include:

1. Theorem of addition of probabilities.

2. Probability multiplication theorem.

Let us consider the theorem of addition of probabilities for a particular case. Let's pretend that A And IN incompatible events, and we will assume that the probabilities of these events are known or can be found.

Theorem 3.1. The probability of the occurrence of one of two incompatible events is equal to the sum of the probabilities of these events, i.e.

Proof. Let n – total number all equally possible elementary events of the test in which events may appear A or IN. Let us denote by t A And t V number of elementary events favorable to events A And IN respectively. Since events A And IN are incompatible, then the sum of these events A + IN favor t A+ t V elementary events. That's why .

The theorem has been proven.

Consequence. The probability of the occurrence of one of several pairwise incompatible events is equal to the sum of the probabilities of these events, i.e.

Proof is not difficult to carry out using the method of mathematical induction.

Example 3.1. A box contains 8 white, 5 black and 10 red balls. One ball is selected at random. What is the probability that this ball is not white?

Solution. Let the event A– choosing a black ball, IN– choosing a red ball. Then the event WITH = A + IN determines the choice of a non-white ball (either black or red).

According to the classical formula . By Theorem 3.1 we finally obtain .■

Example 3.2. The company has two vacant positions, for which three men and five women are applying. Find the probability that among the people hired there will be at least one man if the selection of applicants is carried out randomly.

Solution. Let the event WITH is that among the people hired there will be at least one man. It is obvious that the event WITH will occur when one of the following two incompatible events occurs: A– two men were hired; IN– one woman and one man were hired. Thus, WITH = A + IN.

Let's find the probabilities of events A And IN, using the classical formula, we get

And .

Events A And IN– are inconsistent, therefore, we can apply Theorem 3.1. We get. ■

When solving Example 3.2, the only possible event that was not considered was that two women would be hired. Let's denote it by the letter D and find its probability. Applying the classical formula, we get

.

It is not difficult to understand that events A, IN And D form a complete group for the test: choice of two people out of eight. Let's find the sum of the probabilities of these events: . The obtained result can be presented in general form.

Theorem 3.2. The sum of the probabilities of events forming a complete group is equal to 1.

Proof. Let events A 1 , A 2 , …, A n form a full group for some testing. Then, by definition, as a result of this test, one of the events will definitely occur, i.e. the sum of these events is a certain event. The probability of a reliable event is 1. Therefore, the equality is true:

Recall that, by the definition of a complete group, it consists of incompatible events. Then, by the corollary of Theorem 3.1, we obtain

The theorem has been proven.

Consequence. The sum of the probabilities of opposite events is equal to 1.

Proof it follows directly from the fact that opposite events form a complete group, therefore, by Theorem 3.2, the formula holds

(3.3)

Where A And Ā – opposite events.

The investigation has been proven.

When solving problems, the transformed formula (3.3) is more often used, namely

(3.4)

Example 3.3. Of the nine candidates for selection for the three positions, five graduated with honors. Everyone has the same chance of being selected for these positions. Determine the probability that among those selected there will be at least one with an honors degree.

Solution. Let the event A means that among the selected candidates at least one has an honors degree. It is obvious that the event Ā opposite A will be that all three people selected do not have an honors degree. Let's find the probability of the opposite event. To do this, we apply the classical formula, we get

.

Using formula (3.3) we find the probability of the event A:

. ■

The solution to Example 3.3 can also be obtained in another, longer way. It is not difficult to understand that the event A is the sum of the following events:

A 1 – among those selected there is only one candidate with a diploma with honors;

A 2 – among the selected two candidates with a diploma with honors;

A 3 – among the selected three candidates with a diploma with honors.

Using the classical formula we get

It is obvious that events A 1 , A 2 , A 3 are inconsistent, therefore we can apply Theorem 3.3. Thus

It is clear that the first solution is much simpler.

In the theorems and examples discussed above, the incompatibility of the corresponding random events was assumed. Naturally, a problem may arise in which it is required to find the probability of the occurrence of at least one of the joint events. Theorem 3.1 cannot be applied in this case. There are more general form probability addition theorem, which uses the concept of probability of a product of events.

Theorem for multiplying event probabilities

Let us consider some test in which a random event may occur A. If, apart from the test condition, there are no restrictions for the event A does not exist, then the probability of the event A called unconditional probability. If some questions are asked additional conditions, then appears conditional probability this event. Most often, additional conditions are associated with the occurrence of another random event. So, when analyzing a particular phenomenon, the question may arise: does the possibility of the occurrence of a certain event affect A the occurrence of another random event IN and if it does, how? For example, the offensive IN leads to the obligatory occurrence of an event A or, conversely, excludes the possibility of an event occurring A, or maybe only changes the probability value. It is easy to understand that if an event IN is favorable to the event A, then when the event occurs IN event A always occurs, or if A And IN– two events that are incompatible in a given test, then when the event occurs IN event A will never happen. However, these are so-called edge cases. The greatest interest arises when the occurrence of an event IN somehow changes (increases or decreases) the probability of an event occurring A without turning it into a reliable or impossible event under new conditions. The characteristic of such influence of one event on another is conditional probability.

Conditional probability events A given that IN is called the probability of an event A, calculated under the assumption that the event IN has already happened.

Similarly, we can determine the conditional probability of an event IN, provided that the event A has already happened.

Example 3.4. Let there be 6 white and 8 black balls in an urn. Two balls are randomly removed from the urn one after another without replacing them. Find the probability that the second ball will be white if the first ball was also drawn white?

Solution . Let the event A is that the second ball will be white, and the event IN that the first ball is white. The problem requires finding the probability of an event A, provided that the event IN happened, i.e. find . If the event IN happened, then there are 13 balls left in the urn, of which 5 are white. Therefore, the probability of drawing a white ball from 13, among which 5 are white, is equal to .■

Let us note two points.

Firstly, for the event A not only its conditional probability can be found, but also the so-called total probability of the event, i.e. the probability that the second ball will be white when any ball is chosen first. Finding such a probability will be discussed in paragraph 3.4.

Secondly, the example condition can be changed so that the color of the first selected ball will not affect the probability of the event occurring at all A. We will assume that the balls, after fixing their color, are returned back to the urn. Then, obviously, the probability of the event A does not depend on what color the first ball was chosen, i.e. from the occurrence (or non-occurrence) of an event IN. In this case , i.e. probability of an event A coincides with the conditional probability of this event. The events themselves A And IN are independent in this test.

Two events A And IN are called independent, if the probability of occurrence of each of them does not depend on whether another event appeared or not. Otherwise, the events are called dependent.

From the definition it follows that for independent events A And IN the following formulas are valid:

. (3.5)

Let's get a formula for finding the conditional probability using the classical definition. Let the test consist of n equally possible elementary events. Number of events favoring the event A, equals t A; event IN – t V; the production of events AB – t AB. It is obvious that . Since the event IN favors t V outcomes, of which only t A favor A, then the conditional probability is equal to

. Finally, we get

(3.6)

It is necessary to pay attention to the fact that the denominator in formula (3.6) is different from zero, since by condition the event IN may happen, i.e. t V not equal to zero.

Reasoning similarly, we can obtain a formula for the conditional probability of an event IN: . But since the event AB no different from the event VA And , then the conditional probability of the event IN can be determined by the formula

(3.7)

In the most complete probability theory courses using the axiomatic approach, formulas (3.6) and (3.7) are taken as the definition of conditional probability, and formulas (3.5) are taken as the definition of independent events.

The following probability multiplication theorem directly follows from formulas (3.6) and (3.7).

Theorem 3.2. The probability of the simultaneous occurrence of two random events is equal to the product of the probability of one event and the conditional probability of the other, calculated under the assumption that the first event has already occurred, i.e.

(3.8)

Consequence. The probability of the simultaneous occurrence of several random events is equal to the product of the probability of one event and the conditional probabilities of all others, while the probability of each subsequent event is calculated under the assumption that all previous events have already occurred, i.e.

Example 3.5. There are 20 tickets in the lottery, of which 5 are winning. 3 tickets are randomly selected one after another without return. Determine the probability that the first, second and third tickets will be winning.

Solution. Let the event A is that the winning ticket will be chosen first, the event IN– that the second ticket will be winning and, finally, WITH– the third ticket is winning. It's obvious that .

Conditional probability of an event IN provided that the event A happened, i.e. one winning ticket was selected from the lottery, equal to (there are 19 tickets left, of which 4 are winning).

Conditional probability of an event WITH provided that events A And IN happened, i.e. two winning tickets were selected, equal to .

By the corollary to Theorem 3.2, the probability of the product is equal to

It should be noted that Problem 3.5 can be solved using the classical formula and combinatorics formulas:

.

Theorem 3.2 is true for any random events A And IN. In the special case when events A And IN are independent, the following statement is true.

Theorem 3.3 . Probability of simultaneous occurrence of two incompatible events A And IN is equal to the product of the probabilities of these events, i.e.

Proof. Events A And IN– independent. By Theorem 3.2, taking into account formula (3.5), we obtain

The theorem has been proven.

So, Theorem 3.3 says that the probability of a product of independent events is found by formula (3.9). The converse is also true.

Theorem 3.4. If formula (3.9) is true for two events, then these events are independent.

Let us present several without proof. important properties, valid for independent events.

1. If the event IN does not depend on A, then the event A does not depend on IN.

2. If events A And IN- are independent, then events are independent A And .

3. If two events are independent, then the events opposite to them are also independent.

Theorem 3.3 can be generalized to a finite number of events. However, before doing this, it is necessary to dwell in more detail on the concept of independence of three or more events.

For a group consisting of three or more events, there is the concept of pairwise independence and independence in the aggregate.

Events A 1 , A 2 , …, A n are called pairwise independent, if any two of these events are independent.

Events A 1 , A 2 , …, A n are called independent in the aggregate ( or simply independent), if they are pairwise independent and each event and all possible products of all others are independent.

For example, three events A 1 , A 2 , A 3 are collectively independent if the following events are independent:

A 1 and A 2 , A 1 and A 3 , A 2 and A 3 ,

A 1 and A 2 A 3 , A 2 and A 1 A 3 , A 3 and A 1 A 2 .

Theorem 3.5 . If events A 1 , A 2 , …, A n are independent in the aggregate, then the probability of their simultaneous occurrence is calculated by the formula:

Proof. Let us show that the formula is correct for three events. If there are more than three events, then the validity of the formula is proven by the method of mathematical induction.

So, let's show that . According to the conditions of the event theorem A 1 , A 2 , A 3 are jointly independent. Therefore, for example, two events are independent A 1 A 2 and A 3. According to formula (3.9), we obtain . By event condition A 1 and A 2 are also independent. Applying formula (3.9) to the first factor, we finally obtain .

The theorem has been proven.

It should be noted that if events are pairwise independent, then it does not follow that they will be independent in the aggregate. And, conversely, if events are independent in the aggregate, then they, obviously, by definition, will be pairwise independent.

Let's consider an example of events that are pairwise independent, but collectively dependent.

Example 3.6. Let a box contain 4 identical cards with numbers written on them:

Randomly selects one card. Event A means that you have chosen a card with the number 1 on it, an event IN assumes that the selected card has the number 2, event WITH– number 3. Find out whether events are A, IN And WITH pairwise independent or jointly independent.

Solution. Probability of each event A, IN And WITH can be found using the classic formula (there are 4 cards in total, two of them have numbers 1, 2, 3 respectively): .

Let us show that events A, IN And WITH pairwise independent. Let's choose any two events, for example, A And IN. The probability of their product is , since the simultaneous appearance of numbers 1 and 2 can only be on one card out of four.

Thus, the equality is true . By Theorem 3.4 events A And IN independent. Similarly, we can show the independence of events IN And WITH, as well as events A And WITH. Pairwise independence has been proven.

Let us show that these events are not independent in the aggregate. The probability of the simultaneous occurrence of all three events, i.e. the appearance of all three numbers is equal to , since only one card out of four has all three numbers. The product of the event probabilities is equal to . Thus, , therefore, there is no independence in the aggregate. ■

From the theorem of multiplication of probabilities and the theorem of addition of probabilities of incompatible events, the theorem of addition of probabilities of compatible events directly follows.

\(\blacktriangleright\) If to execute the event \(C\) it is necessary to execute both joint (which can occur simultaneously) events \(A\) and \(B\) (\(C=\(A\) and \( B\)\) ), then the probability of the event \(C\) is equal to the product of the probabilities of the events \(A\) and \(B\) .

Note that if events are incompatible, then the probability of their simultaneous occurrence is equal to \(0\) .

\(\blacktriangleright\) Each event can be represented by a circle. Then if the events are joint, then the circles must intersect. The probability of an event \(C\) is the probability of getting into both circles at the same time.

\(\blacktriangleright\) For example, when throwing a die, find the probability \(C=\) (the number \(6\)).
The event \(C\) can be formulated as \(A=\) (dropping an even number) and \(B=\) (dropping a number divisible by three).
Then \(P\,(C)=P\,(A)\cdot P\,(B)=\dfrac12\cdot \dfrac13=\dfrac16\).

Task 1 #3092

Task level: Equal to the Unified State Exam

The store sells sneakers from two brands: Dike and Ananas. The probability that a randomly selected pair of sneakers will be from Dike is \(0.6\) . Each company can make a mistake in writing its name on sneakers. The probability that Dike will misspell its name is \(0.05\) ; the probability that Ananas will misspell its name is \(0.025\) . Find the probability that a randomly purchased pair of sneakers will have the correct spelling of the company name.

Event A: “a pair of sneakers will be with the correct name” is equal to the sum of events B: “a pair of sneakers will be from Dike and with the correct name” and C: “a pair of sneakers will be from Ananas and with the correct name.”
The probability of event B is equal to the product of the probabilities of the events “the sneakers will be from Dike” and “the name of the company Dike was written correctly”: \ Similarly for event C: \ Hence, \

Answer: 0.96

Task 2 #166

Task level: Equal to the Unified State Exam

If Timur plays with white checkers, then he wins against Vanya with probability 0.72. If Timur plays with black checkers, then he wins against Vanya with probability 0.63. Timur and Vanya play two games, and in the second game they change the color of the checkers. Find the probability that Vanya wins both times.

Vanya wins with white with probability \(0.37\) and with black with probability \(0.28\) . The events “Vanya won from two games with White”\(\ \) and “Vanya won from two games with Black”\(\ \) are independent, then the probability of their simultaneous occurrence is \

Answer: 0.1036

Task 3 #172

Task level: Equal to the Unified State Exam

The entrance to the museum is guarded by two guards. The probability that the eldest of them will forget the walkie-talkie is \(0.2\) , and the probability that the youngest of them will forget the walkie-talkie is \(0.1\) . What is the probability that they will not have a single radio?

Since the events under consideration are independent, the probability of their simultaneous occurrence is equal to the product of their probabilities. Then the required probability is \

Answer: 0.02

Task 4 #167

Task level: Equal to the Unified State Exam

Jumping from a height of 1 meter, Kostya breaks his leg with probability \(0.05\) . Jumping from a height of 1 meter, Vanya breaks his leg with probability \(0.01\) . Jumping from a height of 1 meter, Anton breaks his leg with probability \(0.01\) . Kostya, Vanya and Anton simultaneously jump from a height of 1 meter. What is the probability that only Kostya will break his leg? Round your answer to the nearest thousand.

Events “when jumping from a height of 1 meter, Kostya broke his leg”\(,\ \) “when jumping from a height of 1 meter, Vanya did not break his leg”\(\ \) and “when jumping from a height of 1 meter, Anton did not break his leg”\( \ \) are independent, therefore, the probability of their simultaneous occurrence is equal to the product of their probabilities: \ After rounding we finally get \(0.049\) .

Answer: 0.049

Task 5 #170

Task level: Equal to the Unified State Exam

Maxim and Vanya decided to play bowling. Maxim rightly estimated that on average he gets a strike once every eight throws. Vanya rightly estimated that on average he gets a strike once every five throws. Maxim and Vanya make exactly one throw each (regardless of the result). What is the probability that there will be no strikes among them?

Since the events under consideration are independent, the probability of their simultaneous occurrence is equal to the product of their probabilities. In this case, the probability that Maxim will not get a strike is equal to \ The probability that Vanya will not get a strike is \(1 - 0.2 = 0.8\) . Then the required probability is equal to \[\dfrac(7)(8)\cdot 0.8 = 0.7.\]

Answer: 0.7

Task 6 #1646

Task level: Equal to the Unified State Exam

Anton and Kostya are playing table tennis. The probability that Kostya will hit the table with his signature blow is \(0.9\) . The probability that Anton will win the rally in which Kostya tried to deliver a signature blow is \(0.3\) . Kostya tried to hit the table with his signature blow. What is the probability that Kostya will actually hit with his signature blow and ultimately win this rally?

Since the events under consideration are independent, the probability of their simultaneous occurrence is equal to the product of their probabilities. Moreover, the probability that Anton will not win the rally in which Kostya tried to deliver his signature blow is equal to \(1 - 0.3 = 0.7\) . Then the required probability is equal to \

There will also be tasks for independent decision, to which you can see the answers.

General statement of the problem: the probabilities of some events are known, and you need to calculate the probabilities of other events that are associated with these events. In these problems, there is a need for operations with probabilities such as addition and multiplication of probabilities.

For example, while hunting, two shots are fired. Event A- hitting a duck with the first shot, event B- hit from the second shot. Then the sum of events A And B- hit with the first or second shot or with two shots.

Problems of a different type. Several events are given, for example, a coin is tossed three times. You need to find the probability that either the coat of arms will appear all three times, or that the coat of arms will appear at least once. This is a probability multiplication problem.

Addition of probabilities of incompatible events

Addition of probabilities is used when you need to calculate the probability of a combination or logical sum of random events.

Sum of events A And B denote A + B or A ∪ B. The sum of two events is an event that occurs if and only if at least one of the events occurs. It means that A + B– an event that occurs if and only if the event occurred during observation A or event B, or simultaneously A And B.

If events A And B are mutually inconsistent and their probabilities are given, then the probability that one of these events will occur as a result of one trial is calculated using the addition of probabilities.

Probability addition theorem. The probability that one of two mutually incompatible events will occur is equal to the sum of the probabilities of these events:

For example, while hunting, two shots are fired. Event A– hitting a duck with the first shot, event IN– hit from the second shot, event ( A+ IN) – a hit from the first or second shot or from two shots. So, if two events A And IN– incompatible events, then A+ IN– the occurrence of at least one of these events or two events.

Example 1. There are 30 balls of the same size in a box: 10 red, 5 blue and 15 white. Calculate the probability that a colored (not white) ball will be picked up without looking.

Solution. Let us assume that the event A- “the red ball is taken”, and the event IN- “The blue ball was taken.” Then the event is “a colored (not white) ball is taken.” Let's find the probability of the event A:

and events IN:

Events A And IN– mutually incompatible, since if one ball is taken, then the balls cannot be taken different colors. Therefore, we use the addition of probabilities:

The theorem for adding probabilities for several incompatible events. If events constitute a complete set of events, then the sum of their probabilities is equal to 1:

The sum of the probabilities of opposite events is also equal to 1:

Opposite events form a complete set of events, and the probability of a complete set of events is 1.

Probabilities of opposite events are usually indicated in small letters p And q. In particular,

from which the following formulas for the probability of opposite events follow:

Example 2. The target in the shooting range is divided into 3 zones. The probability that a certain shooter will shoot at the target in the first zone is 0.15, in the second zone – 0.23, in the third zone – 0.17. Find the probability that the shooter will hit the target and the probability that the shooter will miss the target.

Solution: Find the probability that the shooter will hit the target:

Let's find the probability that the shooter will miss the target:

For more complex problems, in which you need to use both addition and multiplication of probabilities, see the page "Various problems involving addition and multiplication of probabilities".

Addition of probabilities of mutually simultaneous events

Two random events are called joint if the occurrence of one event does not exclude the occurrence of a second event in the same observation. For example, when throwing a die the event A The number 4 is considered to be rolled out, and the event IN– rolling an even number. Since 4 is an even number, the two events are compatible. In practice, there are problems of calculating the probabilities of the occurrence of one of the mutually simultaneous events.

Probability addition theorem for joint events. The probability that one of the joint events will occur is equal to the sum of the probabilities of these events, from which the probability of the common occurrence of both events is subtracted, that is, the product of the probabilities. The formula for the probabilities of joint events has the following form:

Since events A And IN compatible, event A+ IN occurs if one of three possible events occurs: or AB. According to the theorem of addition of incompatible events, we calculate as follows:

Event A will occur if one of two incompatible events occurs: or AB. However, the probability of the occurrence of one event from several incompatible events is equal to the sum of the probabilities of all these events:

Likewise:

Substituting expressions (6) and (7) into expression (5), we obtain the probability formula for joint events:

When using formula (8), it should be taken into account that events A And IN can be:

• mutually independent;
• mutually dependent.

Probability formula for mutually independent events:

Probability formula for mutually dependent events:

If events A And IN are inconsistent, then their coincidence is an impossible case and, thus, P(AB) = 0. The fourth probability formula for incompatible events is:

Example 3. In auto racing, when you drive the first car, you have a better chance of winning, and when you drive the second car. Find:

• the probability that both cars will win;
• the probability that at least one car will win;

1) The probability that the first car will win does not depend on the result of the second car, so the events A(the first car wins) and IN(the second car will win) – independent events. Let's find the probability that both cars win:

2) Find the probability that one of the two cars will win:

For more complex problems, in which you need to use both addition and multiplication of probabilities, see the page "Various problems involving addition and multiplication of probabilities".

Solve the addition of probabilities problem yourself, and then look at the solution

Example 4. Two coins are tossed. Event A- loss of the coat of arms on the first coin. Event B- loss of the coat of arms on the second coin. Find the probability of an event C = A + B .

Multiplying Probabilities

Probability multiplication is used when the probability of a logical product of events must be calculated.

In this case, random events must be independent. Two events are said to be mutually independent if the occurrence of one event does not affect the probability of the occurrence of the second event.

Probability multiplication theorem for independent events. Probability of simultaneous occurrence of two independent events A And IN is equal to the product of the probabilities of these events and is calculated by the formula:

Example 5. The coin is tossed three times in a row. Find the probability that the coat of arms will appear all three times.

Solution. The probability that the coat of arms will appear on the first toss of a coin, the second time, and the third time. Let's find the probability that the coat of arms will appear all three times:

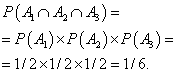
Solve probability multiplication problems on your own and then look at the solution

Example 6. There is a box of nine new tennis balls. To play, three balls are taken, and after the game they are put back. When choosing balls, played balls are not distinguished from unplayed balls. What is the probability that after three games there will be no unplayed balls left in the box?

Example 7. 32 letters of the Russian alphabet are written on cut-out alphabet cards. Five cards are drawn at random one after another and placed on the table in order of appearance. Find the probability that the letters will form the word "end".

Example 8. From a full deck of cards (52 sheets), four cards are taken out at once. Find the probability that all four of these cards will be of different suits.

Example 9. The same task as in example 8, but each card after being removed is returned to the deck.

More complex problems, in which you need to use both addition and multiplication of probabilities, as well as calculate the product of several events, can be found on the page "Various problems involving addition and multiplication of probabilities".

The probability that at least one of the mutually independent events will occur can be calculated by subtracting from 1 the product of the probabilities of opposite events, that is, using the formula.

Probability addition and multiplication theorems.
Dependent and independent events

The title looks scary, but in reality everything is very simple. In this lesson we will get acquainted with the theorems of addition and multiplication of event probabilities, and also analyze typical problems that, along with problem on the classical determination of probability will definitely meet or, more likely, have already met on your way. To effectively study the materials in this article, you need to know and understand the basic terms probability theory and be able to perform simple arithmetic operations. As you can see, very little is required, and therefore a fat plus in the asset is almost guaranteed. But on the other hand, I again warn against a superficial attitude to practical examples - there are also plenty of subtleties. Good luck:

Theorem for adding probabilities of incompatible events: probability of occurrence of one of two incompatible events or (no matter what), is equal to the sum of the probabilities of these events:

A similar fact is true for a larger number of incompatible events, for example, for three incompatible events and:

The theorem is a dream =) However, such a dream is subject to proof, which can be found, for example, in textbook V.E. Gmurman.

Let's get acquainted with new, hitherto unknown concepts:

Dependent and independent events

Let's start with independent events. Events are independent , if the probability of occurrence any of them does not depend on the appearance/non-appearance of other events of the set under consideration (in all possible combinations). ...But why bother trying out general phrases:

Theorem for multiplying the probabilities of independent events: the probability of joint occurrence of independent events and is equal to the product of the probabilities of these events:

Let's return to the simplest example of the 1st lesson, in which two coins are tossed and the following events:

– heads will appear on the 1st coin;
– heads will appear on the 2nd coin.

Let's find the probability of the event (heads will appear on the 1st coin And an eagle will appear on the 2nd coin - remember how to read product of events!) . The probability of heads on one coin does not depend in any way on the result of throwing another coin, therefore, the events are independent.

Likewise:
– the probability that the 1st coin will land heads And on the 2nd tails;
– the probability that heads will appear on the 1st coin And on the 2nd tails;
– probability that the 1st coin will show heads And on the 2nd eagle.

Notice that the events form full group and the sum of their probabilities is equal to one: .

The multiplication theorem obviously extends to a larger number of independent events, for example, if the events are independent, then the probability of their joint occurrence is equal to: . Let's practice with specific examples:

Problem 3

Each of the three boxes contains 10 parts. The first box contains 8 standard parts, the second – 7, the third – 9. One part is randomly removed from each box. Find the probability that all parts will be standard.

Solution: The probability of extracting a standard or non-standard part from any box does not depend on what parts are taken from other boxes, so the problem deals with independent events. Consider the following independent events:

– a standard part is removed from the 1st box;
– a standard part was removed from the 2nd box;
– a standard part is removed from the 3rd box.

According to the classical definition:
are the corresponding probabilities.

Event of interest to us (a standard part will be removed from the 1st box And from 2nd standard And from 3rd standard) is expressed by the product.

According to the theorem of multiplication of probabilities of independent events:

– the probability that one standard part will be removed from three boxes.

Answer: 0,504

After invigorating exercises with boxes, no less interesting urns await us:

Problem 4

Three urns contain 6 white and 4 black balls. One ball is drawn at random from each urn. Find the probability that: a) all three balls will be white; b) all three balls will be the same color.

Based on the information received, guess how to deal with the “be” point ;-) An approximate example of a solution is designed in an academic style with a detailed description of all events.

Dependent Events. The event is called dependent , if its probability depends from one or more events that have already occurred. You don’t have to go far for examples - just go to the nearest store:

– tomorrow at 19.00 fresh bread will be on sale.

The likelihood of this event depends on many other events: whether fresh bread will be delivered tomorrow, whether it will be sold out before 7 pm or not, etc. Depending on various circumstances, this event can be either reliable or impossible. So the event is dependent.

Bread... and, as the Romans demanded, circuses:

– at the exam, the student will receive a simple ticket.

If you are not the very first, then the event will be dependent, since its probability will depend on what tickets have already been drawn by classmates.

How to determine the dependence/independence of events?

Sometimes this is directly stated in the problem statement, but most often you have to conduct an independent analysis. There is no unambiguous guideline here, and the fact of dependence or independence of events follows from natural logical reasoning.

In order not to lump everything into one pile, tasks for dependent events I will highlight the following lesson, but for now we will consider the most common set of theorems in practice:

Problems on addition theorems for incompatible probabilities
and multiplying the probabilities of independent events

This tandem, according to my subjective assessment, works in approximately 80% of tasks on the topic under consideration. Hit of hits and a real classic of probability theory:

Problem 5

Two shooters each fired one shot at the target. The probability of a hit for the first shooter is 0.8, for the second - 0.6. Find the probability that:

a) only one shooter will hit the target;
b) at least one of the shooters will hit the target.

Solution: One shooter's hit/miss rate is obviously independent of the other shooter's performance.

Let's consider the events:
– 1st shooter will hit the target;
– The 2nd shooter will hit the target.

By condition: .

Let's find the probabilities of opposite events - that the corresponding arrows will miss:

a) Consider the event: – only one shooter will hit the target. This event consists of two incompatible outcomes:

1st shooter will hit And 2nd one will miss
or
1st one will miss And The 2nd one will hit.

On the tongue event algebras this fact will be written by the following formula:

First, we use the theorem for adding the probabilities of incompatible events, then the theorem for multiplying the probabilities of independent events:

– the probability that there will be only one hit.

b) Consider the event: – at least one of the shooters hits the target.

First of all, LET’S THINK – what does the condition “AT LEAST ONE” mean? In this case, this means that either the 1st shooter will hit (the 2nd will miss) or 2nd (1st will miss) or both shooters at once - a total of 3 incompatible outcomes.

Method one: taking into account the ready probability of the previous point, it is convenient to represent the event as the sum of the following incompatible events:

someone will get there (an event consisting in turn of 2 incompatible outcomes) or
If both arrows hit, we denote this event with the letter .

Thus:

According to the theorem of multiplication of probabilities of independent events:
– probability that the 1st shooter will hit And The 2nd shooter will hit.

According to the theorem of addition of probabilities of incompatible events:
– the probability of at least one hit on the target.

Method two: Consider the opposite event: – both shooters will miss.

According to the theorem of multiplication of probabilities of independent events:

As a result:

Special attention Pay attention to the second method - in general, it is more rational.

In addition, there is an alternative, third way of solving it, based on the theorem of addition of joint events, which was not mentioned above.

! If you are getting acquainted with the material for the first time, then in order to avoid confusion, it is better to skip the next paragraph.

Method three : the events are compatible, which means their sum expresses the event “at least one shooter will hit the target” (see. algebra of events). By the theorem for adding probabilities of joint events and the theorem of multiplication of probabilities of independent events:

Let's check: events and (0, 1 and 2 hits respectively) form a complete group, so the sum of their probabilities must equal one:
, which was what needed to be checked.

Answer:

With a thorough study of probability theory, you will come across dozens of problems with a militaristic content, and, characteristically, after this you will not want to shoot anyone - the problems are almost a gift. Why not simplify the template as well? Let's shorten the entry:

Solution: by condition: , – probability of hitting the corresponding shooters. Then the probabilities of their miss:

a) According to the theorems of addition of probabilities of incompatible and multiplication of probabilities of independent events:
– the probability that only one shooter will hit the target.

b) According to the theorem of multiplication of probabilities of independent events:
– the probability that both shooters will miss.

Then: – the probability that at least one of the shooters will hit the target.

Answer:

In practice, you can use any design option. Of course, much more often they take the short route, but we must not forget the 1st method - although it is longer, it is more meaningful - it is clearer, what, why and why adds and multiplies. In some cases, a hybrid style is appropriate, when it is convenient to use capital letters to indicate only some events.

Similar tasks for independent solution:

Problem 6

To signal a fire, two independently operating sensors are installed. The probabilities that the sensor will operate in the event of a fire are 0.5 and 0.7, respectively, for the first and second sensors. Find the probability that in a fire:

a) both sensors will fail;
b) both sensors will work.
c) Using the theorem for adding the probabilities of events forming a complete group, find the probability that in a fire only one sensor will work. Check the result by directly calculating this probability (using addition and multiplication theorems).

Here, the independence of the operation of the devices is directly stated in the condition, which, by the way, is an important clarification. The sample solution is designed in an academic style.

What if in a similar problem the same probabilities are given, for example, 0.9 and 0.9? You need to decide exactly the same! (which, in fact, has already been demonstrated in the example with two coins)

Problem 7

The probability of hitting the target by the first shooter with one shot is 0.8. The probability that the target is not hit after the first and second shooters fire one shot each is 0.08. What is the probability of the second shooter hitting the target with one shot?

And this is a small puzzle, which is designed in a short way. The condition can be reformulated more succinctly, but I will not redo the original - in practice, I have to delve into more ornate fabrications.

Meet him - he is the one who has planned an enormous amount of details for you =):

Problem 8

A worker operates three machines. The probability that during a shift the first machine will require adjustment is 0.3, the second - 0.75, the third - 0.4. Find the probability that during the shift:

a) all machines will require adjustment;
b) only one machine will require adjustment;
c) at least one machine will require adjustment.

Solution: since the condition does not say anything about a single technological process, then the operation of each machine should be considered independent of the operation of other machines.

By analogy with Problem No. 5, here you can enter into consideration the events that the corresponding machines will require adjustments during the shift, write down the probabilities, find the probabilities of opposite events, etc. But with three objects, I don’t really want to formulate the task this way – it will turn out long and tedious. Therefore, it is noticeably more profitable to use the “fast” style here:

According to the condition: – the probability that during the shift the corresponding machines will require tuning. Then the probabilities that they will not require attention are:

One of the readers found a cool typo here, I won’t even correct it =)

a) According to the theorem of multiplication of probabilities of independent events:
– the probability that during the shift all three machines will require adjustments.

b) The event “During the shift, only one machine will require adjustment” consists of three incompatible outcomes:

1) 1st machine will require attention And 2nd machine won't require And 3rd machine won't require
or:
2) 1st machine won't require attention And 2nd machine will require And 3rd machine won't require
or:
3) 1st machine won't require attention And 2nd machine won't require And 3rd machine will require.

According to the theorems of addition of probabilities of incompatible and multiplication of probabilities of independent events:

– the probability that during a shift only one machine will require adjustment.

I think by now you should understand where the expression comes from

c) Let’s calculate the probability that the machines will not require adjustment, and then the probability of the opposite event:
– that at least one machine will require adjustment.

Answer:

Point “ve” can also be solved through the sum , where is the probability that during a shift only two machines will require adjustment. This event, in turn, includes 3 incompatible outcomes, which are described by analogy with the “be” point. Try to find the probability yourself to check the whole problem using equality.

Problem 9

A salvo was fired from three guns at the target. The probability of a hit with one shot from only the first gun is 0.7, from the second – 0.6, from the third – 0.8. Find the probability that: 1) at least one projectile will hit the target; 2) only two shells will hit the target; 3) the target will be hit at least twice.

The solution and answer are at the end of the lesson.

And again about coincidences: if, according to the condition, two or even all values ​​of the initial probabilities coincide (for example, 0.7, 0.7 and 0.7), then exactly the same solution algorithm should be followed.

To conclude the article, let’s look at another common puzzle:

Problem 10

The shooter hits the target with the same probability with each shot. What is this probability if the probability of at least one hit with three shots is 0.973.

Solution: let us denote by – the probability of hitting the target with each shot.
and through – the probability of a miss with each shot.

And let’s write down the events:
– with 3 shots the shooter will hit the target at least once;
– the shooter will miss 3 times.

By condition, then the probability of the opposite event:

On the other hand, according to the theorem of multiplication of probabilities of independent events:

Thus:

- the probability of a miss with each shot.

As a result:
– the probability of a hit with each shot.

Answer: 0,7

Simple and elegant.

In the problem considered, additional questions can be asked about the probability of only one hit, only two hits, and the probability of three hits on the target. The solution scheme will be exactly the same as in the two previous examples:

However, the fundamental substantive difference is that here there are repeated independent tests, which are performed sequentially, independently of each other and with the same probability of outcomes.