Sabitlərin dəyişməsi. ODE
Mühazirə 44. İkinci dərəcəli xətti qeyri-bərabər tənliklər. İxtiyari sabitlərin dəyişməsi üsulu. Sabit əmsallı ikinci dərəcəli xətti qeyri-bərabər tənliklər. (xüsusi sağ tərəf).
Sosial çevrilmələr. Dövlət və kilsə.
Sosial siyasət Bolşevikləri əsasən onların sinfi yanaşması diktə edirdi. 1917-ci il 10 noyabr tarixli fərmanla sinfi sistem məhv edildi, inqilabdan əvvəlki rütbələr, titullar və mükafatlar ləğv edildi. Hakimlərin seçkisi müəyyən edilib; sivil dövlətlərin dünyəviləşdirilməsi həyata keçirilirdi. Pulsuz təhsil və tibbi xidmət yaradıldı (31 oktyabr 1918-ci il fərmanı). Qadınlara kişilərlə bərabər hüquqlar verildi (16 və 18 dekabr 1917-ci il fərmanları). Nikah haqqında Fərman vətəndaş nikahı institutunu tətbiq etdi.
Xalq Komissarları Sovetinin 20 yanvar 1918-ci il tarixli qərarı ilə kilsə dövlətdən və təhsil sistemindən ayrıldı. Kilsə əmlakının çox hissəsi müsadirə edildi. Moskva və Bütün Rusiyanın Patriarxı Tixon (5 noyabr 1917-ci ildə seçildi) 1918-ci il yanvarın 19-da sovet hakimiyyətini anathematize etdi və bolşeviklərə qarşı mübarizəyə çağırdı.
Xətti qeyri-bərabər ikinci dərəcəli tənliyi nəzərdən keçirək
Belə bir tənliyin ümumi həllinin strukturu aşağıdakı teoremlə müəyyən edilir:
Teorem 1. Qeyri-bircins tənliyin (1) ümumi həlli bu tənliyin bəzi xüsusi həlli ilə müvafiq homojen tənliyin ümumi həllinin cəmi kimi təmsil olunur.
Sübut. Bu məbləği sübut etmək lazımdır
var ümumi qərar tənlik (1). Əvvəlcə (3) funksiyasının (1) tənliyinin həlli olduğunu sübut edək.
Cəmi (1) tənliyinə əvəz etmək saat, olacaq
(2) tənliyinin həlli olduğundan birinci mötərizədəki ifadə eyni şəkildə sıfıra bərabərdir. (1) tənliyinin həlli olduğundan ikinci mötərizədəki ifadə bərabərdir f(x). Buna görə də bərabərlik (4) eynilikdir. Beləliklə, teoremin birinci hissəsi sübuta yetirilir.
İkinci ifadəni sübut edək: (3) ifadəsidir general(1) tənliyinin həlli. Sübut etməliyik ki, bu ifadəyə daxil olan ixtiyari sabitləri elə seçmək olar ki, ilkin şərtlər yerinə yetirilsin:
rəqəmlər nə olursa olsun x 0 , y 0 və (yalnız əgər x 0 funksiyalarının olduğu ərazidən götürülüb a 1, a 2 Və f(x) davamlı).
şəklində təmsil oluna biləcəyini nəzərə alaraq. Sonra (5) şərtlərinə əsasən bizdə olacaq
Gəlin bu sistemi həll edək və müəyyən edək C 1 Və C 2. Sistemi formada yenidən yazaq:
Qeyd edək ki, bu sistemin determinantı funksiyalar üçün Wronski determinantıdır 1-də Və 2-də nöqtədə x=x 0. Bu funksiyalar şərtə görə xətti müstəqil olduğundan Wronski determinantı sıfıra bərabər deyil; buna görə də (6) sisteminin müəyyən həlli var C 1 Və C 2, yəni. belə mənalar var C 1 Və C 2, hansı düsturla (3) verilmiş ilkin şərtləri təmin edən (1) tənliyinin həllini müəyyən edir. Q.E.D.
Qeyri-homogen tənliyin qismən həllinin tapılmasının ümumi üsuluna keçək.
Homojen tənliyin ümumi həllini yazaq (2)
Biz qeyri-homogen tənliyin (1) xüsusi həllini (7) şəklində axtaracağıq. C 1 Və C 2 bəzi hələ bilinməyən funksiyalar kimi X.
Gəlin bərabərliyi fərqləndirək (7):
Gəlin axtardığınız funksiyaları seçək C 1 Və C 2 bərabərlik təmin olunsun
Bu əlavə şərti nəzərə alsaq, onda birinci törəmə forma alacaq
İndi bu ifadəni fərqləndirərək tapırıq:
(1) tənliyini əvəz edərək, alırıq
İlk iki mötərizədəki ifadələr sıfıra çevrilir, çünki y 1 Və y 2– homojen tənliyin həlli. Buna görə də sonuncu bərabərlik formasını alır
Beləliklə, (7) funksiyası qeyri-bərabər tənliyin (1) həlli olacaqdır C 1 Və C 2(8) və (9) tənliklərini təmin edin. (8) və (9) tənliklərindən tənliklər sistemi yaradaq.
Bu sistemin determinantı xətti müstəqil həllər üçün Wronski determinantıdır y 1 Və y 2 tənliyi (2), onda sıfıra bərabər deyil. Buna görə də, sistemi həll edərək, hər ikisinin müəyyən funksiyalarını tapacağıq X:
Bu sistemi həll edərək, haradan, inteqrasiya nəticəsində əldə edirik. Sonra tapılmış funksiyaları düsturla əvəz edirik, qeyri-bərabər tənliyin ümumi həllini alırıq, burada ixtiyari sabitlər var.
Qeyri-bircins diferensial tənliklərin həlli üçün ixtiyari sabitlərin dəyişməsi üsulundan istifadə olunur. Bu dərs artıq mövzunu az və ya çox yaxşı bilən tələbələr üçün nəzərdə tutulub. Əgər siz uzaqdan idarəetmə ilə yeni tanış olmağa başlayırsınızsa, yəni. Əgər çaydansınızsa, ilk dərsdən başlamağı məsləhət görürəm: Birinci dərəcəli diferensial tənliklər. Həll nümunələri. Əgər siz artıq bitirmisinizsə, lütfən, metodun çətin olduğuna dair mümkün ilkin mülahizədən imtina edin. Çünki sadədir.
İxtiyari sabitlərin dəyişməsi üsulu hansı hallarda tətbiq edilir?
1) Həll etmək üçün ixtiyari sabitin dəyişmə üsulundan istifadə etmək olar 1-ci dərəcəli xətti qeyri-homogen DE. Tənlik birinci dərəcəli olduğundan, sabit də birdir.
2) Bəzilərinin həlli üçün ixtiyari sabitlərin dəyişmə üsulundan istifadə edilir xətti qeyri-homogen ikinci dərəcəli tənliklər. Burada iki sabit dəyişir.
Dərsin iki paraqrafdan ibarət olacağını güman etmək məntiqlidir... Beləliklə, mən bu cümləni yazdım və təxminən 10 dəqiqə ərzində praktiki nümunələrə rəvan keçid üçün başqa hansı ağıllı cəfəngiyyatı əlavə edə biləcəyimi düşündüm. Ancaq nədənsə tətildən sonra heç bir fikrim yoxdur, baxmayaraq ki, heç nədən sui-istifadə etməmişəm. Ona görə də gəlin birbaşa birinci abzasa keçək.
İxtiyari sabitin dəyişmə üsulu
birinci dərəcəli xətti qeyri-bərabər tənlik üçün
İxtiyari sabitin dəyişmə üsulunu nəzərdən keçirməzdən əvvəl məqalə ilə tanış olmaq məsləhətdir. Birinci dərəcəli xətti diferensial tənliklər. Həmin dərsdə məşq etdik ilk həll qeyri-homogen 1-ci dərəcəli DE. Bu ilk həll, sizə xatırladıram, adlanır əvəzetmə üsulu və ya Bernoulli üsulu( ilə qarışdırılmamalıdır Bernoulli tənliyi!!!)
İndi baxacağıq ikinci həll– ixtiyari sabitin dəyişmə üsulu. Mən cəmi üç misal çəkəcəyəm və onları yuxarıda qeyd etdiyim dərsdən götürəcəyəm. Niyə bu qədər azdır? Çünki əslində ikinci şəkildəki həll birinci üsuldakı həllə çox oxşar olacaq. Bundan əlavə, müşahidələrimə görə, ixtiyari sabitlərin dəyişməsi üsulu əvəzetmə üsulundan daha az istifadə olunur.
Misal 1
![]()
(Dərsin 2 nömrəli nümunəsindən fərqlilik 1-ci dərəcəli xətti qeyri-bərabər diferensial tənliklər)
Həll: Bu tənlik xətti qeyri-bərabərdir və tanış formaya malikdir: ![]()
Birinci mərhələdə daha sadə bir tənliyi həll etmək lazımdır: ![]()
Yəni axmaqcasına sağ tərəfi sıfırlayıb yerinə sıfır yazırıq.
tənlik ![]() zəng edəcəm köməkçi tənlik.
zəng edəcəm köməkçi tənlik.
Bu nümunədə aşağıdakı köməkçi tənliyi həll etməlisiniz:
Bizdən əvvəl ayrıla bilən tənlik, bunun həlli (ümid edirəm) sizin üçün artıq çətin deyil: 
Beləliklə: ![]() – köməkçi tənliyin ümumi həlli.
– köməkçi tənliyin ümumi həlli.
İkinci addımda əvəz edəcəyik bəzi daimi hələlik"x"-dən asılı olan naməlum funksiya:
Beləliklə, metodun adı - biz sabiti dəyişirik. Alternativ olaraq, sabit indi tapmalı olduğumuz bəzi funksiya ola bilər.
IN orijinal qeyri-homogen tənlik ![]() əvəz edək:
əvəz edək:
Əvəz edək və ![]() tənliyə daxil
tənliyə daxil ![]() :
:
Nəzarət nöqtəsi - sol tərəfdəki iki şərt ləğv edilir. Bu baş vermirsə, yuxarıdakı xətanı axtarmalısınız.
Əvəzetmə nəticəsində ayrıla bilən dəyişənlərə malik tənlik əldə edilmişdir. Dəyişənləri ayırırıq və inteqrasiya edirik.
Nə yaxşı ki, eksponentlər də ləğv edir:
Tapılmış funksiyaya "normal" sabit əlavə edirik:
Aktiv son mərhələƏvəzimizi xatırlayaq:
Funksiya indicə tapıldı!
Beləliklə, ümumi həll yolu budur: 
Cavab:ümumi qərar: ![]()
İki həlli çap etsəniz, hər iki halda eyni inteqralları tapdığımızı asanlıqla görərsiniz. Fərq yalnız həll alqoritmindədir.
İndi daha mürəkkəb bir şey üçün ikinci nümunəni də şərh edəcəyəm:
Misal 2
Diferensial tənliyin ümumi həllini tapın ![]()
(Dərsin 8-ci nümunəsindən fərqli 1-ci dərəcəli xətti qeyri-bərabər diferensial tənliklər)
Həll: Tənliyi formaya endirək ![]() :
:
Sağ tərəfi sıfırlayaq və köməkçi tənliyi həll edək:
Köməkçi tənliyin ümumi həlli:
Qeyri-homogen tənlikdə əvəz edirik:
Məhsulun fərqləndirmə qaydasına görə: ![]()
Əvəz edək və ![]() orijinal qeyri-homogen tənliyə:
orijinal qeyri-homogen tənliyə:
Sol tərəfdəki iki şərt ləğv edilir, yəni biz düzgün yoldayıq: 
Gəlin hissələrə görə inteqrasiya edək. Hissələr düsturu ilə inteqrasiyadan gələn ləzzətli məktub artıq həlldə iştirak edir, buna görə də, məsələn, "a" və "be" hərflərindən istifadə edirik:
![]()
İndi əvəzetməni xatırlayaq:
Cavab:ümumi qərar:
Və bir misal üçün müstəqil qərar:
Misal 3
Verilmiş ilkin şərtə uyğun gələn diferensial tənliyin xüsusi həllini tapın.
,
(Dərsin 4-cü Nümunəsindən fərqli 1-ci dərəcəli xətti qeyri-bərabər diferensial tənliklər)
Həll:
Bu DE xətti qeyri-bərabərdir. Biz ixtiyari sabitlərin dəyişməsi metodundan istifadə edirik. Köməkçi tənliyi həll edək:
Dəyişənləri ayırırıq və inteqrasiya edirik: 
Ümumi qərar: ![]()
Qeyri-homogen tənlikdə əvəz edirik: ![]()
Əvəzetməni yerinə yetirək: 
Beləliklə, ümumi həll yolu budur: ![]()
Verilmiş ilkin şərtə uyğun olan xüsusi bir həll tapaq: ![]()
Cavab:şəxsi həll:
Dərsin sonundakı həll tapşırığı tamamlamaq üçün nümunə ola bilər.
İxtiyari sabitlərin dəyişməsi üsulu
xətti qeyri-bərabər ikinci dərəcəli tənlik üçün
sabit əmsallarla
Mən tez-tez belə bir fikir eşitmişəm ki, ikinci dərəcəli tənlik üçün ixtiyari sabitləri dəyişmək üsulu asan iş deyil. Ancaq mən aşağıdakıları güman edirəm: çox güman ki, metod çoxları üçün çətin görünür, çünki o, tez-tez baş vermir. Amma əslində heç bir xüsusi çətinlik yoxdur - qərarın gedişatı aydın, şəffaf və başa düşüləndir. Və gözəl.
Metodun mənimsənilməsi üçün sağ tərəfin formasına əsaslanaraq müəyyən bir həll seçməklə qeyri-bərabər ikinci dərəcəli tənlikləri həll edə bilmək arzu edilir. Bu üsul məqalədə ətraflı müzakirə olunur. Qeyri-homogen 2-ci dərəcəli DE-lər. Xatırlayırıq ki, sabit əmsallı ikinci dərəcəli xətti qeyri-bərabər tənliyin forması var:
Yuxarıdakı dərsdə müzakirə edilən seçim metodu yalnız sağ tərəfdə çoxhədlilər, eksponensiallar, sinuslar və kosinuslar olduğu məhdud sayda hallarda işləyir. Bəs sağda, məsələn, bir kəsr, logarifm, tangens olduqda nə etməli? Belə bir vəziyyətdə sabitlərin dəyişməsi üsulu köməyə gəlir.
Misal 4
İkinci dərəcəli diferensial tənliyin ümumi həllini tapın ![]()
Həll: Bu tənliyin sağ tərəfində bir kəsir var, ona görə də dərhal deyə bilərik ki, müəyyən bir həllin seçilməsi metodu işləmir. Biz ixtiyari sabitlərin dəyişməsi metodundan istifadə edirik.
Tufan əlamətləri yoxdur, həllin başlanğıcı tamamilə adidir:
tapacağıq ümumi qərar uyğun homojen tənliklər: ![]()
Xarakterik tənliyi tərtib edib həll edək: ![]()
![]() – birləşmiş kompleks köklər alınır, buna görə də ümumi həll belədir:
– birləşmiş kompleks köklər alınır, buna görə də ümumi həll belədir:
Ümumi həllin qeydinə diqqət yetirin - əgər mötərizələr varsa, onları açın.
İndi biz birinci dərəcəli tənlik üçün demək olar ki, eyni hiyləni edirik: sabitləri dəyişdirərək onları naməlum funksiyalarla əvəz edirik. Yəni, qeyri-homogenin ümumi həlli tənlikləri aşağıdakı formada axtaracağıq:
Harada - hələlik naməlum funksiyalar.

Məişət tullantıları zibilliyinə bənzəyir, amma indi hər şeyi qaydasına salacağıq.
Naməlumlar funksiyaların törəmələridir. Məqsədimiz törəmələri tapmaqdır və tapılan törəmələr sistemin həm birinci, həm də ikinci tənliklərini təmin etməlidir.
"Yunanlar" haradan gəlir? Leylək onları gətirir. Daha əvvəl əldə edilmiş ümumi həllə baxırıq və yazırıq:
Gəlin törəmələri tapaq:
Sol hissələr işlənib. Sağda nə var?
orijinal tənliyin sağ tərəfidir, bu halda:
Əmsal ikinci törəmənin əmsalıdır:
Praktikada, demək olar ki, həmişə və nümunəmiz istisna deyil.
Hər şey aydındır, indi bir sistem yarada bilərsiniz: 
Sistem ümumiyyətlə həll olunur Kramer düsturlarına görə standart alqoritmdən istifadə etməklə. Yeganə fərq ondadır ki, bizdə nömrələrin əvəzinə funksiyalar var.
Sistemin əsas determinantını tapaq: 
Əgər siz ikiyə-iki təyinedicinin necə aşkarlandığını unutmusunuzsa, dərsə müraciət edin Determinantı necə hesablamaq olar? Link ayıb lövhəsinə aparır =)
Beləliklə: bu o deməkdir ki, sistemin unikal həlli var.
Törəməni tapmaq: 
Ancaq bu, hamısı deyil, indiyə qədər yalnız törəməni tapdıq.
Funksiya özü inteqrasiya yolu ilə bərpa olunur:
İkinci funksiyaya baxaq: 
![]()
![]()
Burada “normal” sabiti əlavə edirik
Həllin son mərhələsində qeyri-homogen tənliyin ümumi həllini hansı formada axtardığımızı xatırlayırıq? Belə:
Sizə lazım olan funksiyalar indicə tapıldı! ![]()
Yalnız əvəzetməni yerinə yetirmək və cavabı yazmaq qalır:
Cavab:ümumi qərar:
Prinsipcə, cavab mötərizələri genişləndirə bilərdi.
Cavabın tam yoxlanışı dərsdə müzakirə olunan standart sxemə əsasən aparılır. Qeyri-homogen 2-ci dərəcəli DE-lər. Ancaq yoxlama asan olmayacaq, çünki kifayət qədər ağır törəmələr tapmaq və çətin əvəzetmə aparmaq lazımdır. Bu cür diffuzorları həll edərkən xoşagəlməz bir xüsusiyyətdir.
Misal 5
İxtiyari sabitləri dəyişdirməklə diferensial tənliyi həll edin
![]()
Bu, özünüz həll etməyiniz üçün bir nümunədir. Əslində, sağ tərəfdə də bir kəsir var. Gəlin xatırlayaq triqonometrik düstur, yeri gəlmişkən, həll zamanı tətbiq etmək lazımdır.
İxtiyari sabitlərin dəyişməsi üsulu ən universal üsuldur. Həll edilə bilən hər hansı bir tənliyi həll edə bilər sağ tərəfin formasına əsaslanaraq müəyyən bir həllin seçilməsi üsulu. Sual yaranır: niyə orada da ixtiyari sabitlərin dəyişməsi metodundan istifadə etməyək? Cavab göz qabağındadır: sinifdə müzakirə edilən müəyyən bir həll yolunun seçilməsi Qeyri-homogen ikinci dərəcəli tənliklər, həlli əhəmiyyətli dərəcədə sürətləndirir və qeydi qısaldır - determinantlar və inteqrallarla təlaş yoxdur.
ilə iki misala baxaq Cauchy problemi.
Misal 6
Verilmiş ilkin şərtlərə uyğun gələn diferensial tənliyin xüsusi həllini tapın
![]() ,
, ![]()
Həll: Yenə kəsr və eksponent maraqlı yer.
Biz ixtiyari sabitlərin dəyişməsi metodundan istifadə edirik.
tapacağıq ümumi qərar uyğun homojen tənliklər: ![]()
![]() – müxtəlif həqiqi köklər əldə edilir, buna görə də ümumi həll yolu belədir:
– müxtəlif həqiqi köklər əldə edilir, buna görə də ümumi həll yolu belədir:
Qeyri-homogenin ümumi həlli tənlikləri aşağıdakı formada axtarırıq: , burada - hələlik naməlum funksiyalar.
Gəlin bir sistem yaradaq: 
Bu halda:
,
Törəmələrin tapılması: ![]() ,
, ![]()
![]()
Beləliklə: 
Cramer düsturlarından istifadə edərək sistemi həll edək:
, yəni sistemin unikal həlli var.


Funksiyanı inteqrasiya yolu ilə bərpa edirik:
Burada istifadə olunur funksiyanın diferensial işarəsi altında cəmlənməsi üsulu.


İkinci funksiyanı inteqrasiya yolu ilə bərpa edirik: ![]()
Bu inteqral həll olunur dəyişən əvəzetmə üsulu:
Əvəzetmənin özündən ifadə edirik:
Beləliklə: ![]()
![]()
Bu inteqral tapıla bilər tam kvadrat çıxarma üsulu, lakin diffuzorlu nümunələrdə mən fraksiyanın genişləndirilməsinə üstünlük verirəm üsul qeyri-müəyyən əmsallar
:
Hər iki funksiya tapıldı:
Nəticədə qeyri-homogen tənliyin ümumi həlli belədir:
İlkin şərtləri təmin edən xüsusi bir həll tapaq ![]() .
.
Texniki olaraq, bir həll axtarışı məqalədə müzakirə olunan standart bir şəkildə həyata keçirilir İkinci dərəcəli qeyri-homogen diferensial tənliklər.
Gözləyin, indi tapılan ümumi həllin törəməsini tapacağıq:
Bu belə biabırçılıqdır. Bunu sadələşdirmək lazım deyil, dərhal tənliklər sistemi yaratmaq daha asandır. İlkin şərtlərə görə ![]() :
:

Sabitlərin tapılmış dəyərlərini əvəz edək ![]() ümumi həll yolu:
ümumi həll yolu:
Cavabda loqarifmlər bir az qablaşdırıla bilər.
Cavab:şəxsi həll: ![]()
Gördüyünüz kimi, çətinliklər inteqrallarda və törəmələrdə yarana bilər, lakin ixtiyari sabitlərin dəyişməsi metodunun alqoritmində deyil. Sizi qorxudan mən deyiləm, hamısı Kuznetsovun kolleksiyasıdır!
İstirahət üçün, özünüz həll etmək üçün son, daha sadə bir nümunə:
Misal 7
Cauchy problemini həll edin
![]() ,
, ![]()
Nümunə sadə, lakin yaradıcıdır, bir sistem yaratdığınız zaman qərar verməzdən əvvəl ona diqqətlə baxın ;-),
![]()


![]()
Nəticədə ümumi həll yolu belədir:
Başlanğıc şərtlərə uyğun olan xüsusi bir həll tapaq ![]() .
.
![]()

Sabitlərin tapılmış qiymətlərini ümumi həlldə əvəz edək:
Cavab:şəxsi həll:
İxtiyari sabitin dəyişməsi üsulu və ya Laqranj üsulu birinci dərəcəli xətti diferensial tənlikləri və Bernulli tənliyini həll etməyin başqa bir yoludur.
Birinci dərəcəli xətti diferensial tənliklər y’+p(x)y=q(x) formalı tənliklərdir. Sağ tərəfdə sıfır varsa: y’+p(x)y=0, onda bu xəttidir. homojen 1-ci dərəcəli tənlik. Müvafiq olaraq, sağ tərəfi sıfır olmayan y’+p(x)y=q(x) olan tənlikdir. heterojen 1-ci dərəcəli xətti tənlik.
İxtiyari sabitin dəyişmə üsulu (Laqranj metodu) aşağıdakı kimidir:
1) y’+p(x)y=0: y=y* homojen tənliyinin ümumi həllini axtarırıq.
2) Ümumi həlldə C-ni sabit deyil, x-in funksiyası hesab edirik: C = C (x). Ümumi həllin (y*)’ törəməsini tapırıq və nəticədə y* və (y*)’ ifadəsini ilkin şərtlə əvəz edirik. Alınan tənlikdən C(x) funksiyasını tapırıq.
3) Bircins tənliyin ümumi həllində C əvəzinə tapılmış C(x) ifadəsini əvəz edirik.
İxtiyari sabitin dəyişdirilməsi üsulunun nümunələrinə baxaq. Gəlin eyni tapşırıqları götürək, həllin gedişatını müqayisə edək və alınan cavabların üst-üstə düşdüyünə əmin olun.
1) y’=3x-y/x
Gəlin tənliyi standart formada yenidən yazaq (Bernulli metodundan fərqli olaraq, burada qeyd forması yalnız tənliyin xətti olduğunu görmək üçün lazım idi).
y’+y/x=3x (I). İndi plana uyğun olaraq davam edirik.
1) y’+y/x=0 homojen tənliyini həll edin. Bu, ayrıla bilən dəyişənləri olan bir tənlikdir. Təsəvvür edin y’=dy/dx, əvəz edin: dy/dx+y/x=0, dy/dx=-y/x. Tənliyin hər iki tərəfini dx-ə vurub xy≠0-a bölürük: dy/y=-dx/x. Gəlin inteqrasiya edək:
2) Homojen tənliyin nəticədə ümumi həllində C-ni sabit deyil, x-in funksiyası hesab edəcəyik: C=C(x). Buradan
Yaranan ifadələri (I) şərti ilə əvəz edirik:
Tənliyin hər iki tərəfini birləşdirək:
burada C artıq bəzi yeni sabitdir.
3) C=C(x), yəni y=C(x)/x qəbul etdiyimiz y=C/x bircins tənliyinin ümumi həllində C(x) əvəzinə tapılmış x³ ifadəsini əvəz edirik. +C: y=(x³ +C)/x və ya y=x²+C/x. Bernulli üsulu ilə həll edərkən eyni cavabı aldıq.
Cavab: y=x²+C/x.
2) y’+y=cosx.
Burada tənlik artıq standart formada yazılıb, onu çevirməyə ehtiyac yoxdur.
1) y’+y=0 homojen xətti tənliyini həll edin: dy/dx=-y; dy/y=-dx. Gəlin inteqrasiya edək:
Daha rahat qeyd formasını əldə etmək üçün biz C-nin gücünün göstəricisini yeni C kimi götürürük:
Bu çevrilmə törəmənin tapılmasını daha rahat etmək üçün həyata keçirilmişdir.
2) Xətti bircinsli tənliyin nəticədə ümumi həllində C-ni sabit deyil, x-in funksiyası hesab edirik: C=C(x). Bu şərtlə
![]()
Nəticədə y və y' ifadələrini şərtlə əvəz edirik:
Tənliyin hər iki tərəfini ilə çarpın
Hissələr düsturundan istifadə edərək tənliyin hər iki tərəfini inteqrasiya edirik, alırıq:
Burada C artıq funksiya deyil, adi sabitdir.
3) Homojen tənliyin ümumi həllində
tapılmış C(x) funksiyasını əvəz edin:
Bernulli üsulu ilə həll edərkən eyni cavabı aldıq.
Həll etmək üçün ixtiyari sabitin dəyişmə üsulu da tətbiq olunur.
y'x+y=-xy².
Tənliyi standart formaya gətiririk: y’+y/x=-y² (II).
1) y’+y/x=0 homojen tənliyini həll edin. dy/dx=-y/x. Tənliyin hər iki tərəfini dx-ə vurub y-yə bölürük: dy/y=-dx/x. İndi inteqrasiya edək:
Yaranan ifadələri (II) şərtlə əvəz edirik:
Sadələşdirək:
![]()
C və x üçün ayrıla bilən dəyişənləri olan bir tənlik əldə etdik:
![]()
![]()
Burada C artıq adi sabitdir. İnteqrasiya prosesində qeydi çox yükləməmək üçün C(x) əvəzinə sadəcə C yazdıq. Və sonda C(x)-i yeni C ilə qarışdırmamaq üçün C(x)-ə qayıtdıq.
3) Bircinsli y=C(x)/x tənliyinin ümumi həllində tapılmış C(x) funksiyasını əvəz edirik:
![]()
Bernoulli metodundan istifadə edərək həll edərkən eyni cavabı aldıq.
![]()
Öz-özünə sınaq nümunələri:
1. Tənliyi standart formada yenidən yazaq: y’-2y=x.
1) y’-2y=0 homojen tənliyini həll edin. y’=dy/dx, deməli, dy/dx=2y, tənliyin hər iki tərəfini dx-ə vurub, y-yə bölün və inteqral edin:
Buradan y tapırıq:
Şərtdə y və y' ifadələrini əvəz edirik (qısalıq üçün C(x) əvəzinə C və C"(x) əvəzinə C' istifadə edəcəyik):
Sağ tərəfdəki inteqralı tapmaq üçün hissələr üzrə inteqrasiya düsturundan istifadə edirik:
![]()
İndi u, du və v-ni düsturda əvəz edirik:
Burada C =const.
3) İndi məhlulda homojeni əvəz edirik
Laqranj sabitlərinin dəyişməsi üsulu ilə sabit əmsallı daha yüksək dərəcəli xətti qeyri-bərabər diferensial tənliklərin həlli üsulu nəzərdən keçirilir. Laqranj metodu, əgər homojen tənliyin əsas həllər sistemi məlumdursa, istənilən xətti qeyri-homogen tənliklərin həlli üçün də tətbiq olunur.
MəzmunHəmçinin bax:
Laqranj metodu (sabitlərin dəyişməsi)
İxtiyari n-ci dərəcəli sabit əmsalları olan xətti qeyri-bərabər diferensial tənliyi nəzərdən keçirək:
(1)
.
Birinci dərəcəli tənlik üçün nəzərdə tutduğumuz sabitin dəyişmə üsulu daha yüksək dərəcəli tənliklər üçün də tətbiq edilir.
Həll iki mərhələdə həyata keçirilir. İlk addımda sağ tərəfi atırıq və homojen tənliyi həll edirik. Nəticə etibarı ilə n ixtiyari sabitdən ibarət həlli əldə edirik. İkinci mərhələdə biz sabitləri dəyişirik. Yəni biz hesab edirik ki, bu sabitlər müstəqil x dəyişənin funksiyalarıdır və bu funksiyaların formasını tapırıq.
Baxmayaraq ki, biz burada sabit əmsallı tənlikləri nəzərdən keçiririk, lakin Laqranj metodu istənilən xətti qeyri-bərabər tənliklərin həlli üçün də tətbiq olunur. Bunun üçün isə homojen tənliyin əsas həllər sistemi məlum olmalıdır.
Addım 1. Homojen tənliyin həlli
Birinci dərəcəli tənliklərdə olduğu kimi, biz əvvəlcə homojen tənliyin ümumi həllini axtarırıq, sağ tərəfdəki qeyri-bərabər tərəfi sıfıra bərabərləşdiririk:
(2)
.
Bu tənliyin ümumi həlli belədir:
(3)
.
Budur ixtiyari sabitlər; - bu tənliyin əsas həllər sistemini təşkil edən bircins tənliyin (2) xətti müstəqil n həlli.
Addım 2. Sabitlərin dəyişməsi - sabitlərin funksiyalarla əvəz edilməsi
İkinci mərhələdə biz sabitlərin dəyişməsi ilə məşğul olacağıq. Başqa sözlə, sabitləri müstəqil x dəyişəninin funksiyaları ilə əvəz edəcəyik:
.
Yəni, orijinal tənliyin (1) aşağıdakı formada həllini axtarırıq:
(4)
.
Əgər (4)-ü (1) əvəz etsək, n funksiya üçün bir diferensial tənlik alırıq. Bu halda biz bu funksiyaları əlavə tənliklərlə birləşdirə bilərik. Onda siz n funksiyanın təyin oluna biləcəyi n tənlik alırsınız. Əlavə tənliklər yazıla bilər fərqli yollar. Amma biz bunu elə edəcəyik ki, həll ən sadə formaya malik olsun. Bunun üçün diferensiallaşdırarkən funksiyaların törəmələrini ehtiva edən şərtləri sıfıra bərabərləşdirmək lazımdır. Gəlin bunu nümayiş etdirək.
Təklif olunan həlli (4) orijinal tənliyə (1) əvəz etmək üçün (4) şəklində yazılmış funksiyanın ilk n sıralarının törəmələrini tapmaq lazımdır. Cəmin və məhsulun fərqləndirmə qaydalarından istifadə edərək (4) fərqləndiririk:
.
Gəlin üzvləri qruplaşdıraq. Əvvəlcə törəmələri olan şərtləri, sonra isə törəmələri olan şərtləri yazırıq:
.
Birinci şərti funksiyalara qoyaq:
(5.1)
.
Onda birinci törəmə üçün ifadə daha sadə formada olacaq:
(6.1)
.
Eyni üsuldan istifadə edərək ikinci törəməni tapırıq:
.
Funksiyalara ikinci şərt qoyaq:
(5.2)
.
Sonra
(6.2)
.
Və s. IN əlavə şərtlər, funksiyaların törəmələrini ehtiva edən terminləri sıfıra bərabərləşdiririk.
Beləliklə, funksiyalar üçün aşağıdakı əlavə tənlikləri seçsək:
(5.k) ,
onda ilk törəmələr ən sadə formaya sahib olacaqlar:
(6.k) .
Budur.
n-ci törəməni tapın:
(6.n)
.
Orijinal tənliyi (1) əvəz edin:
(1)
;
.
Nəzərə alaq ki, bütün funksiyalar (2) tənliyini təmin edir:
.
Sonra sıfırı ehtiva edən şərtlərin cəmi sıfır verir. Nəticədə əldə edirik:
(7)
.
Nəticədə bir sistem əldə etdik xətti tənliklər törəmələr üçün:
(5.1)
;
(5.2)
;
(5.3)
;
. . . . . . .
(5.n-1) ;
(7′) .
Bu sistemi həll edərək, x-in funksiyası kimi törəmələr üçün ifadələr tapırıq. İnteqrasiya edərək əldə edirik:
.
Budur, artıq x-dən asılı olmayan sabitlər. (4)-i əvəz edərək, orijinal tənliyin ümumi həllini əldə edirik.
Qeyd edək ki, törəmələrin dəyərlərini təyin etmək üçün a i əmsallarının sabit olması faktından heç vaxt istifadə etməmişik. Buna görə də Laqranj metodu istənilən xətti qeyri-bərabər tənlikləri həll etmək üçün tətbiq olunur, əgər homojen tənliyin (2) əsas həllər sistemi məlumdursa.
Nümunələr
Sabitlərin dəyişməsi metodundan (Laqranj) istifadə edərək tənlikləri həll edin.
Nümunələrin həlli > > >
Bernulli metodundan istifadə edərək daha yüksək dərəcəli tənliklərin həlli
Sabit əmsallı daha yüksək dərəcəli xətti qeyri-homogen diferensial tənliklərin xətti əvəzetmə yolu ilə həlli
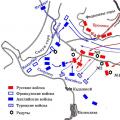 Balaclava döyüşü Balaclava döyüşü
Balaclava döyüşü Balaclava döyüşü İmperator I Paul və onun sevimli İvan Pavloviç Kutaisov
İmperator I Paul və onun sevimli İvan Pavloviç Kutaisov Şahzadə Vsevolod III Novqorod ilə Böyük Yuva Münasibətləri
Şahzadə Vsevolod III Novqorod ilə Böyük Yuva Münasibətləri