İnteqrasiyanın ən mühüm xüsusiyyətləri. Qeyri-müəyyən inteqralın əsas xassələri
Qoy funksiya olsun y = f(x) intervalında müəyyən edilir [ a, b ], a < b. Aşağıdakı əməliyyatları yerinə yetirək:
1) ayrılaq [ a, b] nöqtələr a = x 0 < x 1 < ... < x i- 1 < x i < ... < x n = b haqqında n qismən seqmentlər [ x 0 , x 1 ], [x 1 , x 2 ], ..., [x i- 1 , x i ], ..., [x n- 1 , x n ];
2) qismən seqmentlərin hər birində [ x i- 1 , x i ], i = 1, 2, ... n, ixtiyari bir nöqtə seçin və bu nöqtədə funksiyanın dəyərini hesablayın: f(z i ) ;
3) əsərləri tapın f(z i ) · Δ x i , qismən seqmentin uzunluğu haradadır [ x i- 1 , x i ], i = 1, 2, ... n;
4) gəlin barışaq inteqral cəmi funksiyaları y = f(x) seqmentdə [ a, b ]:
Həndəsi nöqteyi-nəzərdən bu cəm σ əsasları qismən seqmentlər olan düzbucaqlıların sahələrinin cəmidir [ x 0 , x 1 ], [x 1 , x 2 ], ..., [x i- 1 , x i ], ..., [x n- 1 , x n ] və hündürlüklər bərabərdir f(z 1 ) , f(z 2 ), ..., f(z n) müvafiq olaraq (Şəkil 1). ilə işarə edək λ ən uzun qismən seqmentin uzunluğu:
5) zaman inteqral cəminin limitini tapın λ → 0.
Tərif.Əgər (1) inteqral cəminin sonlu həddi varsa və o, seqmentin bölmə metodundan asılı deyilsə [ a, b] qismən seqmentlərə, nə də nöqtələrin seçimindən z i onlarda, sonra bu hədd adlanır müəyyən inteqral funksiyasından y = f(x) seqmentdə [ a, b] və işarələnir
Beləliklə,
Bu halda funksiya f(x) adlanır inteqrasiya oluna bilən on [ a, b]. Nömrələri a Və b müvafiq olaraq inteqrasiyanın aşağı və yuxarı həddi adlanır, f(x) – inteqral funksiya, f(x ) dx- inteqral ifadə, x – inteqrasiya dəyişəni; xətt seqmenti [ a, b] inteqrasiya intervalı adlanır.
Teorem 1.Əgər funksiyası y = f(x) [ intervalında davamlıdır a, b], onda bu intervalda inteqral edilə bilər.
İnteqrasiya hədləri eyni olan müəyyən inteqral sıfıra bərabərdir:
Əgər a > b, onda tərifə görə biz fərz edirik
2. Müəyyən inteqralın həndəsi mənası
Seqmentə qoyun [ a, b] davamlı qeyri-mənfi funksiya təyin olunur y = f(x ) . Əyrixətli trapesiya yuxarıda funksiyanın qrafiki ilə məhdudlaşdırılmış rəqəmdir y = f(x), aşağıdan - Ox oxu boyunca, sola və sağa - düz xətlər x = a Və x = b(Şəkil 2).
Mənfi olmayan funksiyanın müəyyən inteqralı y = f(x) həndəsi baxımdan sahəsinə bərabərdir yuxarıda funksiyanın qrafiki ilə məhdudlaşan əyrixətti trapesiya y = f(x), sol və sağ – xətt seqmentləri x = a Və x = b, aşağıdan - Ox oxunun bir seqmenti.
3. Müəyyən inteqralın əsas xassələri
1. Müəyyən inteqralın qiyməti inteqrasiya dəyişəninin təyinatından asılı deyil:
2. Müəyyən inteqralın işarəsindən sabit amili çıxarmaq olar:
3. İki funksiyanın cəbri cəminin müəyyən inteqralı bu funksiyaların müəyyən inteqrallarının cəbri cəminə bərabərdir:
4.Əgər funksiyası y = f(x) inteqrasiya olunur [ a, b] Və a < b < c, Bu
5. (orta dəyər teoremi). Əgər funksiyası y = f(x) [ intervalında davamlıdır a, b], onda bu seqmentdə elə bir məqam var ki
4. Nyuton-Leybnits düsturu
Teorem 2.Əgər funksiyası y = f(x) [ intervalında davamlıdır a, b] Və F(x) bu seqmentdə onun antiderivativlərindən hər hansı biri olarsa, aşağıdakı düstur etibarlıdır:
adlanır Nyuton-Leybnits düsturu. Fərq F(b) - F(a) adətən aşağıdakı kimi yazılır:
burada simvol ikiqat joker adlanır.
Beləliklə, düstur (2) belə yazıla bilər:
Misal 1.İnteqralı hesablayın
Həll. İnteqral üçün f(x ) = x 2 ixtiyari antiderivativ formaya malikdir
Nyuton-Leybniz düsturunda hər hansı bir antitörəmə istifadə oluna biləcəyi üçün inteqralı hesablamaq üçün ən sadə formaya malik olan antitörəmə götürürük:
5. Müəyyən inteqralda dəyişənin dəyişməsi
Teorem 3. Qoy funksiya olsun y = f(x) [ intervalında davamlıdır a, b]. Əgər:
1) funksiya x = φ ( t) və onun törəməsi φ "( t) üçün davamlıdır;
2) funksiya qiymətlərinin çoxluğu x = φ ( t) seqmentdir [ a, b ];
3) φ ( a) = a, φ ( b) = b, onda düstur etibarlıdır
adlanır müəyyən inteqralda dəyişəni dəyişdirmək üçün düstur .
Fərqli qeyri-müəyyən inteqral, bu halda lazım deyil orijinal inteqrasiya dəyişəninə qayıtmaq üçün - α və β inteqrasiyasının yeni hədlərini tapmaq kifayətdir (bunun üçün dəyişən üçün həll etməlisiniz. t tənliklər φ ( t) = a və φ ( t) = b).
Əvəz etmək əvəzinə x = φ ( t) əvəzetmədən istifadə edə bilərsiniz t = g(x) . Bu halda, dəyişən üzərində inteqrasiyanın yeni hədlərinin tapılması t sadələşdirir: α = g(a) , β = g(b) .
Misal 2. İnteqralı hesablayın
Həll. Düsturdan istifadə edərək yeni dəyişən təqdim edək. Bərabərliyin hər iki tərəfini kvadratlaşdıraraq 1+ alırıq x = t 2 , harada x = t 2 - 1, dx = (t 2 - 1)"dt= 2tdt. Biz inteqrasiyanın yeni sərhədlərini tapırıq. Bunu etmək üçün köhnə limitləri düsturla əvəz edək x = 3 və x = 8. Alırıq: , haradan t= 2 və α = 2; , harada t= 3 və β = 3. Beləliklə,
Misal 3. Hesablayın
Həll. Qoy u= log x, Sonra , v = x. Formula (4) görə
İnteqralların həlli asan məsələdir, lakin yalnız seçilmiş bir neçə nəfər üçün. Bu məqalə inteqralları başa düşməyi öyrənmək istəyən, lakin onlar haqqında heç nə və ya demək olar ki, heç nə bilməyənlər üçündür. İnteqral... Niyə lazımdır? Onu necə hesablamaq olar? Müəyyən və qeyri-müəyyən inteqrallar hansılardır?
Əgər inteqral üçün bildiyiniz yeganə istifadə əlçatmaz yerlərdən faydalı bir şey əldə etmək üçün inteqral simvol kimi formalı qarmaqdan istifadə etməkdirsə, xoş gəlmisiniz! Ən sadə və digər inteqralları necə həll edəcəyinizi və riyaziyyatda niyə onsuz edə bilməyəcəyinizi öyrənin.
Konsepsiyanı öyrənirik « inteqral »
İnteqrasiya əvvəldən məlum idi Qədim Misir. Əlbətdə yox müasir forma, ancaq hələ də. O vaxtdan bəri riyaziyyatçılar bu mövzuda çoxlu kitablar yazmışlar. Xüsusilə özlərini fərqləndirdilər Nyuton Və Leybniz , lakin şeylərin mahiyyəti dəyişməyib.
İnteqralları sıfırdan necə başa düşmək olar? Heç bir şəkildə! Bu mövzunu başa düşmək üçün hələ də riyazi analizin əsasları haqqında əsas biliklərə ehtiyacınız olacaq. Bloqumuzda artıq inteqralları anlamaq üçün lazım olan haqqında məlumat var.
Qeyri-müəyyən inteqral
Gəlin bəzi funksiyalarımız olsun f(x) .
Qeyri-müəyyən inteqral funksiya f(x) bu funksiya adlanır F(x) törəməsi funksiyasına bərabər olan f(x) .
Başqa sözlə, inteqral tərs törəmə və ya antitörəmədir. Yeri gəlmişkən, məqaləmizdə necə olduğunu oxuyun.

Bütün davamlı funksiyalar üçün antitörəmə mövcuddur. Həm də antitörəmə tez-tez sabit işarə əlavə olunur, çünki sabit ilə fərqlənən funksiyaların törəmələri üst-üstə düşür. İnteqralın tapılması prosesi inteqrasiya adlanır.
Sadə misal:

Elementar funksiyaların antitörəmələrini daim hesablamamaq üçün onları cədvələ qoymaq və hazır qiymətlərdən istifadə etmək rahatdır.
Tələbələr üçün inteqralların tam cədvəli

Müəyyən inteqral
İnteqral anlayışı ilə məşğul olarkən, biz sonsuz kiçik kəmiyyətlərlə məşğul oluruq. İnteqral bir fiqurun sahəsini, qeyri-bərabər bir cismin kütləsini, qeyri-bərabər hərəkət zamanı qət edilən məsafəni və daha çoxunu hesablamağa kömək edəcəkdir. Yadda saxlamaq lazımdır ki, inteqral sonsuz cəmdir böyük miqdar sonsuz kiçik şərtlər.
Nümunə olaraq hansısa funksiyanın qrafikini təsəvvür edin.

Funksiya qrafiki ilə məhdudlaşan fiqurun sahəsini necə tapmaq olar? İnteqraldan istifadə edin! Koordinat oxları və funksiyanın qrafiki ilə məhdudlaşan əyrixətti trapesiyanı sonsuz kiçik seqmentlərə bölək. Bu şəkildə rəqəm nazik sütunlara bölünəcəkdir. Sütunların sahələrinin cəmi trapezoidin sahəsi olacaqdır. Ancaq unutmayın ki, belə bir hesablama təxmini nəticə verəcəkdir. Lakin seqmentlər nə qədər kiçik və dar olarsa, hesablama bir o qədər dəqiq olacaqdır. Onları uzunluq sıfıra enəcək qədər azaldsaq, seqmentlərin sahələrinin cəmi rəqəmin sahəsinə meyl edəcəkdir. Bu, müəyyən bir inteqraldır və belə yazılmışdır:

a və b nöqtələrinə inteqrasiyanın hədləri deyilir.

« İnteqral »
Yeri gəlmişkən! Oxucularımız üçün artıq 10% endirim var
Dummiyalar üçün inteqralların hesablanması qaydaları
Qeyri-müəyyən inteqralın xassələri
Qeyri-müəyyən inteqralı necə həll etmək olar? Burada qeyri-müəyyən inteqralın xassələrinə baxacağıq ki, bu da misalların həlli zamanı faydalı olacaq.
- İnteqralın törəməsi inteqrana bərabərdir:

- Sabit inteqral işarəsi altından çıxarıla bilər:

- Cəmin inteqralı inteqralların cəminə bərabərdir. Bu, fərq üçün də doğrudur:
Müəyyən inteqralın xassələri
- Xəttilik:

- İnteqrasiya hədləri dəyişdirildikdə inteqralın işarəsi dəyişir:

- At hər hansı xal a, b Və ilə:

Artıq müəyyən inteqralın cəminin həddi olduğunu öyrəndik. Bəs nümunəni həll edərkən konkret dəyəri necə əldə etmək olar? Bunun üçün Nyuton-Leybniz düsturu var:

İnteqralların həlli nümunələri
Aşağıda qeyri-müəyyən inteqralı və həlli ilə nümunələri nəzərdən keçirəcəyik. Həllin incəliklərini özünüz anlamanızı təklif edirik və bir şey aydın deyilsə, şərhlərdə suallar verin.

Materialı möhkəmləndirmək üçün inteqralların praktikada necə həll edildiyi haqqında videoya baxın. İnteqral dərhal verilməzsə, ümidsiz olmayın. Tələbələr üçün peşəkar xidmətlə əlaqə saxlayın və qapalı səth üzərində istənilən üçlü və ya əyri inteqral sizin səlahiyyətinizdə olacaq.
Bu xassələrdən inteqralın elementar inteqrallardan birinə endirilməsi və sonrakı hesablanması üçün onun çevrilmələrini həyata keçirmək üçün istifadə olunur.
1. Qeyri-müəyyən inteqralın törəməsi inteqrana bərabərdir:
2. Qeyri-müəyyən inteqralın diferensialı inteqrana bərabərdir:
3. Müəyyən funksiyanın diferensialının qeyri-müəyyən inteqralı bu funksiyanın cəminə və ixtiyari sabitə bərabərdir:
4. Sabit əmsalı inteqral işarəsindən çıxarmaq olar:
Üstəlik, a ≠ 0
5. Cəminin (fərqinin) inteqralı inteqralların cəminə (fərqinə) bərabərdir:
6. Mülk 4 və 5-ci xassələrin birləşməsidir:
Bundan əlavə, a ≠ 0 ˄ b ≠ 0
7. Qeyri-müəyyən inteqralın dəyişməzlik xassəsi:
Əgər, onda
8. Əmlak:
Əgər, onda
Əslində, bu xassə, növbəti bölmədə daha ətraflı müzakirə olunan dəyişən dəyişmə metodundan istifadə edərək inteqrasiyanın xüsusi halıdır.
Bir misala baxaq:
Əvvəlcə 5-ci xassəni, sonra 4-cü xassəni tətbiq etdik, sonra antiderivativlər cədvəlindən istifadə etdik və nəticəni aldıq.
Onlayn inteqral kalkulyatorumuzun alqoritmi yuxarıda sadalanan bütün xassələri dəstəkləyir və inteqralınız üçün asanlıqla ətraflı həll tapacaqdır.
Bu məqalədə müəyyən inteqralın əsas xüsusiyyətləri haqqında ətraflı danışılır. Onlar Riemann və Darboux inteqralının konsepsiyasından istifadə etməklə sübut edilmişdir. Müəyyən bir inteqralın hesablanması 5 xassə sayəsində baş verir. Qalanları müxtəlif ifadələri qiymətləndirmək üçün istifadə olunur.
Müəyyən inteqralın əsas xassələrinə keçməzdən əvvəl a-nın b-dən çox olmamasına əmin olmaq lazımdır.
Müəyyən inteqralın əsas xassələri
Tərif 1x = a-da təyin olunan y = f (x) funksiyası ∫ a a f (x) d x = 0 ədalətli bərabərliyinə bənzəyir.
Sübut 1
Buradan görərik ki, hədləri üst-üstə düşən inteqralın qiyməti sıfıra bərabərdir. Bu, Rieman inteqralının nəticəsidir, çünki [ a intervalında hər hansı bölmə üçün hər bir inteqral cəmi σ; a ] və ζ i nöqtələrinin istənilən seçimi sıfıra bərabərdir, çünki x i - x i - 1 = 0 , i = 1 , 2 , . . . , n, yəni inteqral funksiyaların limitinin sıfır olduğunu tapırıq.
Tərif 2
[a intervalında inteqral oluna bilən funksiya üçün; b ] , ∫ a b f (x) d x = - ∫ b a f (x) d x şərti ödənilir.
Sübut 2
Başqa sözlə, inteqrasiyanın yuxarı və aşağı hədlərini dəyişdirsəniz, inteqralın qiyməti əks qiymətə dəyişəcəkdir. Bu əmlak Riemann inteqralından götürülmüşdür. Bununla belə, seqmentin bölməsinin nömrələnməsi x = b nöqtəsindən başlayır.
Tərif 3
∫ a b f x ± g (x) d x = ∫ a b f (x) d x ± ∫ a b g (x) d x [ a intervalında müəyyən edilmiş y = f (x) və y = g (x) tipli inteqrallana bilən funksiyalara aiddir; b].
Sübut 3
Verilmiş ζ i nöqtələri ilə seqmentlərə bölmək üçün y = f (x) ± g (x) funksiyasının inteqral cəmini yazın: σ = ∑ i = 1 n f ζ i ± g ζ i · x i - x i - 1 = = ∑ i = 1 n f (ζ i) · x i - x i - 1 ± ∑ i = 1 n g ζ i · x i - x i - 1 = σ f ± σ g
burada σ f və σ g seqmenti bölmək üçün y = f (x) və y = g (x) funksiyalarının inteqral cəmidir. λ = m a x i = 1, 2, -də limitə keçdikdən sonra. . . , n (x i - x i - 1) → 0 alırıq ki, lim λ → 0 σ = lim λ → 0 σ f ± σ g = lim λ → 0 σ g ± lim λ → 0 σ g .
Riemanın tərifindən bu ifadə ekvivalentdir.
Tərif 4
Sabit əmsalın müəyyən inteqralın işarəsindən kənara uzadılması. [a] intervalından inteqrasiya olunmuş funksiya; b ] ixtiyari dəyəri olan k ∫ a b k · f (x) d x = k · ∫ a b f (x) d x şəklində ədalətli bərabərsizliyə malikdir.
Sübut 4
Müəyyən inteqral mülkiyyətin sübutu əvvəlkinə bənzəyir:
σ = ∑ i = 1 n k · f ζ i · (x i - x i - 1) = = k · ∑ i = 1 n f ζ i · (x i - x i - 1) = k · σ f ⇒ lim λ → 0 σ = lim λ → 0 (k · σ f) = k · lim λ → 0 σ f ⇒ ∫ a b k · f (x) d x = k · ∫ a b f (x) d x
Tərif 5
y = f (x) formalı funksiya a ∈ x, b ∈ x olan x intervalında inteqral oluna bilirsə, alırıq ki, ∫ a b f (x) d x = ∫ a c f (x) d x + ∫ c b f (x) d olsun. x.
Sübut 5
Mülk c ∈ a üçün etibarlı sayılır; b, c ≤ a və c ≥ b üçün. Sübut əvvəlki xüsusiyyətlərə bənzəyir.
Tərif 6
Funksiya seqmentdən inteqrasiya oluna bildikdə [a; b ], onda bu istənilən daxili c seqmenti üçün mümkündür; d ∈ a ; b.
Sübut 6
Sübut Darboux xassəsinə əsaslanır: əgər seqmentin mövcud bölməsinə xallar əlavə olunarsa, onda aşağı Darboux cəmi azalmayacaq, yuxarı isə artmayacaq.
Tərif 7
Funksiya [a; b ] istənilən x ∈ a dəyəri üçün f (x) ≥ 0 f (x) ≤ 0-dan; b , onda alırıq ki, ∫ a b f (x) d x ≥ 0 ∫ a b f (x) ≤ 0 .
Bu xassə Rieman inteqralının tərifindən istifadə etməklə isbat edilə bilər: f (x) ≥ 0 f (x) ≤ 0 qeyri-mənfi olması şərti ilə seqmentin bölmə nöqtələrinin və ζ i nöqtələrinin istənilən seçimi üçün istənilən inteqral cəmi. .
Sübut 7
y = f (x) və y = g (x) funksiyaları [ a intervalında inteqral oluna bilirsə; b ] olarsa, aşağıdakı bərabərsizliklər etibarlı hesab olunur:
∫ a b f (x) d x ≤ ∫ a b g (x) d x , f (x) ≤ g (x) ∀ x ∈ a ; b ∫ a b f (x) d x ≥ ∫ a b g (x) d x , f (x) ≥ g (x) ∀ x ∈ a ; b
Bəyanat sayəsində inteqrasiyanın icazəli olduğunu bilirik. Bu nəticə digər xüsusiyyətlərin sübutunda istifadə olunacaq.
Tərif 8
İnteqrallana bilən funksiya üçün [ a intervalından y = f (x) ; b ] ∫ a b f (x) d x ≤ ∫ a b f (x) d x şəklində ədalətli bərabərsizliyə sahibik.
Sübut 8
Bizdə belədir - f (x) ≤ f (x) ≤ f (x) . Əvvəlki xassədən biz müəyyən etdik ki, bərabərsizliyi həd-həd inteqral etmək olar və o, formanın bərabərsizliyinə uyğun gəlir - ∫ a b f (x) d x ≤ ∫ a b f (x) d x ≤ ∫ a b f (x) d x . Bu ikiqat bərabərsizliyi başqa formada da yazmaq olar: ∫ a b f (x) d x ≤ ∫ a b f (x) d x .
Tərif 9
y = f (x) və y = g (x) funksiyaları [ a intervalından inteqral edildikdə; b ] g (x) üçün ≥ 0 istənilən x ∈ a üçün; b , m · ∫ a b g (x) d x ≤ ∫ a b f (x) · g (x) d x ≤ M · ∫ a b g (x) d x şəklində bərabərsizliyi alırıq, burada m = m i n x ∈ a ; b f (x) və M = m a x x ∈ a ; b f (x) .
Sübut 9
Sübut oxşar şəkildə həyata keçirilir. M və m [a seqmentindən müəyyən edilmiş y = f (x) funksiyasının ən böyük və ən kiçik qiymətləri hesab olunur; b ] , onda m ≤ f (x) ≤ M . İkiqat bərabərsizliyi y = g (x) funksiyasına vurmaq lazımdır ki, bu da m g (x) ≤ f (x) g (x) ≤ M g (x) formasının ikiqat bərabərsizliyinin qiymətini verəcəkdir. [a] intervalında inteqrasiya etmək lazımdır; b ] , onda biz ifadənin sübuta yetirilməsini alırıq.
Nəticə: g (x) = 1 üçün bərabərsizlik m · b - a ≤ ∫ a b f (x) d x ≤ M · (b - a) formasını alır.
İlk orta düstur
Tərif 10y = f (x) üçün [ a intervalında inteqrasiya olunur; b ] ilə m = m i n x ∈ a ; b f (x) və M = m a x x ∈ a ; b f (x) μ ∈ m ədədi var; ∫ a b f (x) d x = μ · b - a uyğun olan M .
Nəticə: y = f (x) funksiyası [ a intervalından kəsilməz olduqda; b ], onda c ∈ a ədədi var; ∫ a b f (x) d x = f (c) b - a bərabərliyini təmin edən b.
Ümumiləşdirilmiş formada birinci orta düstur
Tərif 11y = f (x) və y = g (x) funksiyaları [ a intervalından inteqral oluna bildikdə; b ] ilə m = m i n x ∈ a ; b f (x) və M = m a x x ∈ a ; b f (x) , və istənilən x ∈ a dəyəri üçün g (x) > 0; b. Buradan əldə edirik ki, μ ∈ m ədədi var; ∫ a b f (x) · g (x) d x = μ · ∫ a b g (x) d x bərabərliyini təmin edən M .
İkinci orta düstur
Tərif 12y = f (x) funksiyası [ a intervalından inteqral oluna bildikdə; b ], və y = g (x) monotondur, onda c ∈ a olan ədəd var; b , burada ∫ a b f (x) · g (x) d x = g (a) · ∫ a c f (x) d x + g (b) · ∫ c b f (x) d x şəklində ədalətli bərabərliyi əldə edirik.
Mətndə xəta görsəniz, onu vurğulayın və Ctrl+Enter düymələrini basın
Antitörəmə funksiyası və qeyri-müəyyən inteqral
Fakt 1. İnteqrasiya diferensiasiyanın tərs hərəkətidir, yəni funksiyanın bu funksiyanın məlum törəməsindən bərpasıdır. Beləliklə, funksiya bərpa edildi F(x) adlanır antitörəmə funksiyası üçün f(x).
Tərif 1. Funksiya F(x f(x) müəyyən intervalda X, bütün dəyərlər üçün x bu intervaldan bərabərlik qüvvədədir F "(x)=f(x), yəni bu funksiya f(x) antitörəmə funksiyasının törəməsidir F(x). .
Məsələn, funksiya F(x) = günah x funksiyasının əks törəməsidir f(x) = cos x bütün say xəttində, çünki x-in istənilən dəyəri üçün (günah x)" = (çünki x) .
Tərif 2. Funksiyanın qeyri-müəyyən inteqralı f(x) onun bütün antiderivativlərinin çoxluğudur. Bu vəziyyətdə qeyd istifadə olunur
∫
f(x)dx
,işarəsi haradadır ∫ inteqral işarəsi, funksiyası adlanır f(x) – inteqral funksiyası və f(x)dx – inteqral ifadəsi.
Beləliklə, əgər F(x) – üçün bəzi antitörəmə f(x), Bu
∫
f(x)dx = F(x) +C
Harada C - ixtiyari sabit (sabit).
Qeyri-müəyyən inteqral kimi funksiyanın əks törəmələri çoxluğunun mənasını başa düşmək üçün aşağıdakı bənzətmə uyğundur. Bir qapı olsun (ənənəvi taxta qapı). Onun funksiyası “qapı olmaq”dır. Qapı nədən hazırlanır? Ağacdan hazırlanmışdır. Bu o deməkdir ki, “qapı olmaq” funksiyasının, yəni qeyri-müəyyən inteqralının əks törəmələri çoxluğu “ağac olmaq + C” funksiyasıdır, burada C sabitdir, bu kontekstdə hansı məsələn, ağacın növünü bildirir. Qapının ağacdan bəzi alətlərdən istifadə edilərək düzəldilməsi kimi, funksiyanın törəməsi də antitörəmə funksiyasından istifadə edərək “hazırlanır”. törəməni öyrənərkən öyrəndiyimiz düsturlar .
Sonra ümumi obyektlərin və onlara uyğun antitörəmələrin funksiyaları cədvəli (“qapı olmaq” - “ağac olmaq”, “qaşıq olmaq” - “metal olmaq” və s.) əsas cədvələ bənzəyir. aşağıda veriləcək qeyri-müəyyən inteqrallar. Qeyri-müəyyən inteqrallar cədvəlində bu funksiyaların “yaratıldığı” antitörəmələrin göstəricisi ilə ümumi funksiyalar verilmişdir. Qeyri-müəyyən inteqralın tapılması məsələlərinin bir hissəsində çox səy göstərmədən, yəni qeyri-müəyyən inteqrallar cədvəlindən istifadə etməklə birbaşa inteqrasiya oluna bilən inteqrallar verilir. Daha mürəkkəb məsələlərdə əvvəlcə inteqral çevrilməlidir ki, cədvəl inteqrallarından istifadə olunsun.
Fakt 2. Funksiyanı antiderivativ kimi bərpa edərkən ixtiyari sabiti (sabit) nəzərə almalıyıq. C, və 1-dən sonsuza qədər müxtəlif sabitlərə malik antitörəmələrin siyahısını yazmamaq üçün ixtiyari sabiti olan antitörəmələr toplusunu yazmaq lazımdır. C məsələn, belə: 5 x³+C. Beləliklə, antiderivativin ifadəsinə ixtiyari bir sabit (sabit) daxil edilir, çünki antitörəmə funksiya ola bilər, məsələn, 5 x³+4 və ya 5 x³+3 və fərqləndirildikdə 4 və ya 3 və ya hər hansı digər sabit sıfıra keçir.
Gəlin inteqrasiya problemini qoyaq: bu funksiya üçün f(x) belə bir funksiya tapın F(x), kimin törəməsi bərabərdir f(x).
Misal 1. Funksiyanın əks törəmələri çoxluğunu tapın
Həll. Bu funksiya üçün antitörəmə funksiyadır
Funksiya F(x) funksiyası üçün antitörəmə adlanır f(x), törəmə olarsa F(x) bərabərdir f(x) və ya eyni şey olan diferensial F(x) bərabərdir f(x) dx, yəni.
![]() (2)
(2)
Deməli, funksiya funksiyanın əks törəməsidir. Bununla belə, bu, üçün yeganə antiderivativ deyil. Onlar həm də funksiya kimi xidmət edirlər
Harada İLƏ– ixtiyari sabit. Bunu diferensiasiya yolu ilə yoxlamaq olar.
Beləliklə, bir funksiya üçün bir antitörəmə varsa, onun üçün sabit bir terminlə fərqlənən sonsuz sayda antitörəmə var. Funksiya üçün bütün əks törəmələr yuxarıdakı formada yazılır. Bu, aşağıdakı teoremdən irəli gəlir.
Teorem (2-ci faktın rəsmi ifadəsi).Əgər F(x) – funksiya üçün antitörəmə f(x) müəyyən intervalda X, sonra üçün hər hansı digər antiderivativ f(x) eyni intervalda formada təmsil oluna bilər F(x) + C, Harada İLƏ– ixtiyari sabit.
Növbəti misalda qeyri-müəyyən inteqralın xassələrindən sonra 3-cü bənddə veriləcək inteqrallar cədvəlinə müraciət edirik. Bütün cədvəli oxumadan əvvəl bunu edirik ki, yuxarıdakıların mahiyyəti aydın olsun. Cədvəldən və xassələrdən sonra inteqrasiya zamanı onlardan tam şəkildə istifadə edəcəyik.
Misal 2. Antitörəmə funksiyalar toplusunu tapın:
Həll. Bu funksiyaların “yaratıldığı” antitörəmə funksiyalar toplusunu tapırıq. İnteqrallar cədvəlindən düsturları qeyd edərkən, hələlik qəbul edin ki, orada belə düsturlar var və biz qeyri-müəyyən inteqrallar cədvəlinin özünü bir az daha öyrənəcəyik.
1) üçün inteqrallar cədvəlindən (7) düsturunun tətbiqi n= 3, alırıq
![]()
2) üçün inteqrallar cədvəlindən (10) düsturundan istifadə etməklə n= 1/3, bizdə var
3) O vaxtdan bəri
sonra (7) düsturuna uyğun olaraq n= -1/4 tapırıq
![]()
İnteqral işarəsi altında yazılan funksiyanın özü deyil. f, və onun məhsulu diferensialdır dx. Bu, ilk növbədə hansı dəyişən tərəfindən antiderivativin axtarıldığını göstərmək üçün edilir. Misal üçün,
![]() ,
,
![]() ;
;
burada hər iki halda inteqral bərabərdir, lakin hesab edilən hallarda onun qeyri-müəyyən inteqralları fərqli olur. Birinci halda bu funksiya dəyişənin funksiyası kimi qəbul edilir x, ikincisində isə - funksiyası kimi z .
Funksiyanın qeyri-müəyyən inteqralının tapılması prosesinə həmin funksiyanın inteqrasiyası deyilir.
Qeyri-müəyyən inteqralın həndəsi mənası
Tutaq ki, bir əyri tapmaq lazımdır y=F(x) və biz artıq bilirik ki, onun hər bir nöqtəsindəki tangens bucağının tangensi verilmiş funksiyadır f(x) bu nöqtənin absisi.
Törəmənin həndəsi mənasına görə əyrinin verilmiş nöqtəsindəki tangensin meyl bucağının tangensi y=F(x) törəmənin dəyərinə bərabərdir F"(x). Beləliklə, belə bir funksiyanı tapmaq lazımdır F(x), hansı üçün F"(x)=f(x). Tapşırıqda tələb olunan funksiya F(x)-nin antitörəməsidir f(x). Problemin şərtləri bir əyri ilə deyil, əyrilər ailəsi tərəfindən ödənilir. y=F(x)- bu əyrilərdən biri və hər hansı digər əyri ondan ox boyunca paralel köçürmə yolu ilə əldə edilə bilər ay.
-nin əks törəmə funksiyasının qrafikini adlandıraq f(x) inteqral əyri. Əgər F"(x)=f(x), sonra funksiyanın qrafiki y=F(x) inteqral əyri var.
Fakt 3. Qeyri-müəyyən inteqral həndəsi olaraq bütün inteqral əyrilər ailəsi ilə təmsil olunur. , aşağıdakı şəkildəki kimi. Hər bir əyrinin koordinatların başlanğıcından olan məsafəsi ixtiyari inteqrasiya sabiti ilə müəyyən edilir C.

Qeyri-müəyyən inteqralın xassələri
Fakt 4. Teorem 1. Qeyri-müəyyən inteqralın törəməsi inteqrana, diferensialı isə inteqrana bərabərdir.
Fakt 5. Teorem 2. Funksiya diferensialının qeyri-müəyyən inteqralı f(x) funksiyasına bərabərdir f(x) sabit müddətə qədər , yəni.
![]() (3)
(3)
1 və 2-ci teoremlər göstərir ki, diferensiallaşma və inteqrasiya qarşılıqlı tərs əməllərdir.
Fakt 6. Teorem 3. İnteqraldakı sabit amili qeyri-müəyyən inteqralın işarəsindən çıxarmaq olar. , yəni.
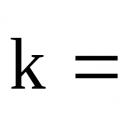 Reaksiya tezliyi sabiti Laboratoriya işi üçün göstərişlər
Reaksiya tezliyi sabiti Laboratoriya işi üçün göstərişlər Ölümdən sonra həyat varmı?
Ölümdən sonra həyat varmı? Alimlər: Yer bəşəriyyət alimləri üçün “kosmik həbsxanadır”: Yer kainatda kosmik həbsxanadır
Alimlər: Yer bəşəriyyət alimləri üçün “kosmik həbsxanadır”: Yer kainatda kosmik həbsxanadır