ناقلات الاستعمارية. الإحداثيات والمتجهات
تاريخ الإنشاء: 2009-04-11 15:25:51
آخر تعديل: 2012-02-08 09:19:45
لفترة طويلة لم أرغب في كتابة هذا المقال - كنت أفكر في كيفية تقديم المادة. تحتاج أيضًا إلى رسم الصور. لكن يبدو أن النجوم قد اصطفت بشكل جيد اليوم وسيكون هناك مقال عن المتجهات. على الرغم من أن هذه مجرد مسودة. في المستقبل، سأقسم هذه المقالة إلى عدة مقالات منفصلة - هناك ما يكفي من المواد. كما ستتحسن المقالة تدريجيًا: سأقوم بإجراء تغييرات عليها - لأن... لن تتمكن من تغطية جميع الجوانب في جلسة واحدة.
تم إدخال المتجهات إلى الرياضيات في القرن التاسع عشر لوصف الكميات التي كان من الصعب وصفها باستخدام القيم العددية.
يتم استخدام المتجهات بشكل مكثف في التطوير العاب كمبيوتر. يتم استخدامها ليس فقط بشكل تقليدي - لوصف كميات مثل القوة أو السرعة، ولكن أيضًا في المناطق التي يبدو أنها لا علاقة لها بالمتجهات: تخزين اللون، وإنشاء الظلال.
العددية والمتجهات
أولاً، اسمحوا لي أن أذكركم ما هي الكمية القياسية وكيف تختلف عن المتجه.
تخزن القيم العددية بعض الكمية: الكتلة والحجم. أي أنه كيان يتميز برقم واحد فقط (كمية شيء مثلاً).
يتم وصف المتجه، على عكس العددية، باستخدام قيمتين: الحجم والاتجاه.
فرق مهم بين المتجهات والإحداثيات: المتجهات غير مرتبطة بموقع محدد! مرة أخرى، الشيء الرئيسي في المتجه هو طوله واتجاهه.
تتم الإشارة إلى المتجه بحرف غامق من الأبجدية اللاتينية. على سبيل المثال: أ, ب, الخامس.
في الشكل الأول يمكنك أن ترى كيف يتم تعيين المتجه على المستوى.
المتجهات في الفضاء
في الفضاء، يمكن التعبير عن المتجهات باستخدام الإحداثيات. لكن علينا أولاً أن نقدم مفهوماً واحداً:
ناقل نصف القطر للنقطة
لنأخذ نقطة ما M(2,1) في الفضاء. متجه نصف القطر لنقطة ما هو متجه يبدأ من نقطة الأصل وينتهي عند النقطة.
ما لدينا هنا ليس أكثر من ناقل أوم. إحداثيات بداية المتجه هي (0,0)، وإحداثيات النهاية هي (2,1). نشير إلى هذا المتجه باسم أ.
في هذه الحالة، يمكن كتابة المتجه على النحو التالي أ = <2, 1>. هذا هو الشكل الإحداثي للمتجه أ.
تسمى إحداثيات المتجه مكوناته نسبة إلى المحاور. على سبيل المثال، 2 هو مكون متجه أنسبة إلى المحور x.
دعونا ننظر مرة أخرى إلى ما هي إحداثيات نقطة ما. إحداثيات النقطة (على سبيل المثال x) هي إسقاط النقطة على المحور، أي. قاعدة العمودي المرسوم من نقطة إلى محور. في مثالنا 2.
ولكن دعونا نعود إلى الرسم الأول. لدينا هنا النقطتان A وB. ولتكن إحداثيات النقطتين (1,1) و(3,3). المتجه الخامسفي هذه الحالة يمكن الإشارة إليه على النحو التالي الخامس = <3-1, 3-1>. سيبدو المتجه الموجود عند نقطتين في مساحة ثلاثية الأبعاد كما يلي:
الخامس =
أعتقد أنه لا توجد صعوبات هنا.
ضرب المتجه بكمية قياسية
يمكن ضرب المتجه بالقيم العددية:
ك الخامس =
في هذه الحالة، يتم ضرب القيمة العددية في كل مكون من مكونات المتجه.
إذا كان k > 1، فإن المتجه سيزداد؛ وإذا كان k أقل من واحد ولكنه أكبر من الصفر، فسيقل طول المتجه. إذا كانت k أقل من الصفر، فإن المتجه سيغير اتجاهه.
ناقلات الوحدة
متجهات الوحدة هي ناقلات طولها يساوي واحدًا. لاحظ أن المتجه ذو الإحداثيات<1,1,1>لن يساوي واحد! يتم وصف العثور على طول المتجه أدناه في النص.
هناك ما يسمى بمتجهات الوحدة - وهي متجهات وحدة تتزامن في الاتجاه مع محاور الإحداثيات. أنا- متجه الوحدة للمحور x، ي- متجه الوحدة للمحور y، ك- متجه الوحدة للمحور z.
حيث أنا = <1,0,0>, ي = <0,1,0>, ك = <0,0,1>.
الآن نحن نعرف ما هو ضرب المتجه بكمية قياسية وما هي متجهات الوحدة. الآن يمكننا أن نكتب الخامسفي شكل ناقلات.
الخامس= الخامس س أنا+ الخامس ذ ي+ الخامس ض ك، حيث v x , v y , v z هي المكونات المقابلة للمتجه
إضافة المتجهات
لفهم الصيغة السابقة بشكل كامل، عليك أن تفهم كيفية عمل إضافة المتجهات.
كل شيء بسيط هنا. لنأخذ متجهين v1 =
ت 1 + ت 2 =
نحن فقط نضيف المكونات المقابلة لمتجهين.
يتم حساب الفرق بنفس الطريقة.
هذا فيما يتعلق بالشكل الرياضي. للحصول على الاكتمال، من المفيد التفكير في الشكل الذي سيبدو عليه جمع المتجهات وطرحها بيانيًا.

لإضافة ناقلين أ+ب. نحن بحاجة إلى محاذاة بداية المتجه بونهاية المتجه أ. ثم بين بداية المتجه أونهاية المتجه برسم ناقلات جديدة. وللتوضيح انظر الصورة الثانية (الحرف "أ").
لطرح المتجهات، تحتاج إلى الجمع بين بدايات متجهين ورسم متجه جديد من نهاية المتجه الثاني إلى نهاية المتجه الأول. الصورة الثانية (الحرف "ب") توضح كيف تبدو.
طول المتجهات واتجاهها
دعونا ننظر إلى الطول أولا.
الطول هو قيمة عدديةناقلات، دون النظر إلى الاتجاه.
يتم تحديد الطول بواسطة الصيغة (للمتجه ثلاثي الأبعاد):
الجذر التربيعي لمجموع مربعات مكونات المتجه.
صيغة مألوفة، أليس كذلك؟ بشكل عام، هذه هي صيغة طول المقطع
يتم تحديد اتجاه المتجه من خلال اتجاه جيب التمام للزوايا المتكونة بين المتجه ومحاور الإحداثيات. للعثور على اتجاه جيب التمام، يتم استخدام المكونات والطول المقابلين (ستأتي الصورة لاحقًا).
تمثيل المتجهات في البرامج
يمكنك تمثيل المتجهات في البرامج طرق مختلفة. سواء بمساعدة المتغيرات العادية، وهي غير فعالة، أو بمساعدة المصفوفات والفئات والهياكل.
تعويم Vector3 = (1،2،3)؛ // مصفوفة لتخزين بنية متجهة 3 // بنية لتخزين المتجهات ( float x,y,z; );
توفر لنا الفصول الدراسية أكبر الفرص لتخزين المتجهات. في الفئات، يمكننا وصف ليس فقط المتجه نفسه (المتغيرات)، ولكن أيضًا عمليات المتجه (الوظائف).
المنتج النقطي للمتجهات
هناك نوعان من ضرب المتجهات: المتجه والعددي.
السمة المميزة للمنتج العددي هي أن النتيجة ستكون دائمًا قيمة عددية، أي. رقم.
وهنا يجدر الانتباه إلى هذه النقطة. إذا كانت نتيجة هذه العملية صفرًا، فإن المتجهين متعامدان، والزاوية بينهما 90 درجة. وإذا كانت النتيجة أكبر من الصفر، تكون الزاوية أقل من 90 درجة. وإذا كانت النتيجة أقل من الصفر، تكون الزاوية أكبر من 90 درجة.
يتم تمثيل هذه العملية بالصيغة التالية:
أ · ب= أ س * ب س + أ ص * ب ص + أ ض * ب ض
المنتج النقطي هو مجموع منتجات المكونات المقابلة لمتجهين. أولئك. نحن نأخذ x لمتجهين، ونضربهما، ثم نضيفهما إلى حاصل ضرب y وهكذا.
منتج متجه من المتجهات
ستكون نتيجة الضرب الاتجاهي لمتجهين متجهًا عموديًا على هذين المتجهين.
لن نناقش هذه الصيغة بالتفصيل في الوقت الحالي. وبالإضافة إلى ذلك، فمن الصعب أن نتذكر. وسنعود إلى هذه النقطة بعد التعرف على المحددات.
حسنًا، للتطوير العام من المفيد معرفة أن طول المتجه الناتج يساوي مساحة متوازي الأضلاع المبني على المتجهات أو ب.
التطبيع المتجهات
المتجه المقيس هو متجه طوله واحد.
صيغة العثور على متجه تم تسويته هي كما يلي - يجب تقسيم جميع مكونات المتجه على طوله:
الخامسن = الخامس/|الخامس| =
خاتمة
كما رأيت على الأرجح، ليس من الصعب فهم المتجهات. نظرنا إلى عدد من العمليات على المتجهات.
وفي المقالات التالية في قسم "الرياضيات" سنناقش المصفوفات والمحددات وأنظمة المعادلات الخطية. هذه كلها نظرية.
بعد ذلك، سوف ننظر إلى تحويلات المصفوفة. عندها ستفهم مدى أهمية الرياضيات في إنشاء ألعاب الكمبيوتر. سيصبح هذا الموضوع تدريبًا على جميع المواضيع السابقة.
تعريف يتم استدعاء مجموعة مرتبة من (x 1 , x 2 , ... , x n) n من الأعداد الحقيقية ناقلات الأبعاد ن، والأرقام x i (i = 1,...,n) - عناصر،أو الإحداثيات,
مثال. على سبيل المثال، إذا كان مصنع سيارات معين يجب أن ينتج 50 سيارة و100 شاحنة و10 حافلات و50 مجموعة من قطع غيار السيارات و150 مجموعة للشاحنات والحافلات في كل وردية عمل، فيمكن كتابة برنامج الإنتاج لهذا المصنع كمتجه (50، 100، 10، 50، 150)، مكونة من خمسة مكونات.
الرموز. تتم الإشارة إلى المتجهات بأحرف صغيرة غامقة أو أحرف مع شريط أو سهم في الأعلى، على سبيل المثال. أأو . يتم استدعاء المتجهين متساويإذا كان لديهم نفس عدد المكونات وكانت المكونات المقابلة لها متساوية.
لا يمكن تبديل مكونات المتجهات، على سبيل المثال، (3، 2، 5، 0، 1) و (2، 3، 5، 0، 1) متجهات مختلفة.
العمليات على المتجهات.العملس= (x 1 , x 2 , ... ,x n) للعدد الحقيقي lect يسمى المتجه lect س= (× × 1، × × 2، ...، × × ن).
كميةس= (x 1 , x 2 , ... ,x n) و ذ= (y 1 , y 2 , ... ,y n) يسمى متجهًا س+ص= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).
مساحة المتجهات.ن-الفضاء المتجه الأبعاد ريتم تعريف n على أنها مجموعة جميع المتجهات ذات الأبعاد n التي يتم من خلالها تحديد عمليات الضرب بالأعداد الحقيقية والجمع.
التوضيح الاقتصادي. التوضيح الاقتصادي لمساحة المتجهات ذات الأبعاد n: مساحة البضائع (بضائع). تحت بضائعسوف نفهم بعض السلع أو الخدمات التي يتم طرحها للبيع في وقت معين في مكان معين. لنفترض أن هناك عددا محدودا من السلع المتاحة؛ وتتميز كميات كل منها التي يشتريها المستهلك بمجموعة من السلع
س= (س 1، س 2، ...، س ن)،
حيث تشير x i إلى مقدار السلعة i التي اشتراها المستهلك. سنفترض أن جميع السلع تتمتع بخاصية القابلية للقسمة التعسفية، بحيث يمكن شراء أي كمية غير سالبة من كل منها. إذن جميع مجموعات البضائع الممكنة هي ناقلات لمساحة البضائع C = ( س= (x 1 , x 2 , ... , x n) x i ≥ 0, i =1,...,n).
الاستقلال الخطي. نظام ه 1 , ه 2 , ... , هتسمى النواقل ذات الأبعاد n تعتمد خطيا، إذا كان هناك أرقام π 1 , ẫ 2 , ... , ẫ m ، يكون أحدها على الأقل غير صفر بحيث تكون المساواة lect 1 ه 1 + μم هم = 0؛ خلاف ذلك، يسمى هذا النظام من المتجهات مستقل خطيا، أي أن المساواة المشار إليها ممكنة فقط في الحالة التي يكون فيها الكل 1 = 2 =...= 1 م =0. المعنى الهندسي للاعتماد الخطي للمتجهات في ر 3، تفسر على أنها شرائح موجهة، اشرح النظريات التالية.
النظرية 1. النظام الذي يتكون من متجه واحد يعتمد خطيًا إذا وفقط إذا كان هذا المتجه صفرًا.
النظرية 2. لكي يكون المتجهان معتمدين خطياً، من الضروري والكافي أن يكونا على خط واحد (متوازيين).
النظرية 3 . لكي تكون ثلاثة نواقل مستقلة خطياً، من الضروري والكافي أن تكون متحدة المستوى (تقع في نفس المستوى).
ثلاثية اليسار واليمين من المتجهات. ثلاثية من المتجهات غير متحدة المستوى أ، ب، جمُسَمًّى يمينإذا تجاوز الراصد من أصلهما المشترك أطراف المتجهات أ، ب، جبالترتيب المعطى يبدو أنه يحدث في اتجاه عقارب الساعة. خلاف ذلك أ، ب، ج -غادر ثلاثة. يتم استدعاء جميع ثلاثيات المتجهات اليمنى (أو اليسرى). نفس الشيء الموجهة.
الأساس والإحداثيات. الترويكا ه 1, ه 2 , ه 3 ناقلات غير متحدة المستوى في ر 3 يسمى أساس، والمتجهات نفسها ه 1, ه 2 , ه 3 - أساسي. أي ناقل أيمكن توسيعها بشكل فريد إلى ناقلات أساسية، أي ممثلة في النموذج
أ= × 1 ه 1+x2 ه 2 + × 3 ه 3, (1.1)
يتم استدعاء الأرقام x 1 , x 2 , x 3 في التوسع (1.1). الإحداثياتأفي الأساس ه 1, ه 2 , ه 3 وتم تعيينهم أ(× 1، × 2، × 3).
أساس متعامد. إذا كانت ناقلات ه 1, ه 2 , ه 3 أزواج متعامدة وطول كل منها يساوي واحدا، فيسمى الأساس متعامد، والإحداثيات × 1، × 2، × 3 - مستطيلي.سيتم الإشارة إلى المتجهات الأساسية للأساس المتعامد بواسطة ط، ي، ك.
وسوف نفترض ذلك في الفضاء ر 3 تم تحديد النظام الصحيح للإحداثيات المستطيلة الديكارتية (0، ط، ي، ك}.
ناقلات العمل الفني.ناقلات العمل الفنيأإلى المتجه بيسمى ناقل ج، والذي يتم تحديده بالشروط الثلاثة التالية:
1. طول المتجه جيساوي عدديًا مساحة متوازي الأضلاع المبني على المتجهات أو ب،أي.
ج= |أ||ب|الخطيئة( أ^ب).
2. المتجهات جعمودي على كل من المتجهات أو ب.
3. المتجهات أ، بو ج، مأخوذة بالترتيب المشار إليه، تشكل ثلاثية صحيحة.
لمنتج متقاطع جتم تقديم التعيين ج =[أب] أو
ج = أ × ب.
إذا كانت ناقلات أو بعلى خط مستقيم، ثم الخطيئة( أ ^ ب) = 0 و [ أب] = 0، على وجه الخصوص، [ أأ] = 0. منتجات المتجهات لمتجهات الوحدة: [ اي جاي]=ك، [jk] = أنا, [كي]=ي.
إذا كانت ناقلات أو بالمحددة في الأساس ط، ي، كالإحداثيات أ(أ 1، أ 2، أ 3)، ب(ب1، ب2، ب3)، ثم


عمل مختلط. إذا كان المنتج المتجه لمتجهين أو بمضروبة بشكل عددي بالمتجه الثالث ج،ثم يسمى هذا المنتج من ثلاثة ناقلات عمل مختلطويشار إليه بالرمز أ ب ج.
إذا كانت ناقلات أ، بو جفي الأساس ط، ي، كنظرا لإحداثياتهم
أ(أ 1، أ 2، أ 3)، ب(ب1، ب2، ب3)، ج(ج1، ج2، ج3)، ثم
 .
.
المنتج المختلط له تفسير هندسي بسيط - فهو عددي، يساوي القيمة المطلقة لحجم متوازي السطوح المبني على ثلاثة ناقلات معينة.
إذا شكلت المتجهات ثلاثيًا قائمًا، فإن منتجها المختلط يكون رقمًا موجبًا يساوي الحجم المشار إليه؛ إذا كان ثلاثة أ، ب، ج -اليسار، ثم أ ب ج<0 и V = - أ ب جوبالتالي V = |أ ب ج|.
من المفترض أن تكون إحداثيات المتجهات التي تمت مواجهتها في مسائل الفصل الأول معطاة بالنسبة إلى الأساس المتعامد الصحيح. وحدة المتجه codirectional مع المتجه أ،يشار إليه بالرمز أيا. رمز ص=أوميُشار إليه بمتجه نصف القطر للنقطة M أو الرموز a أو AB أو |أ|, |أ ب|يتم الإشارة إلى وحدات المتجهات أو أ.ب.
مثال 1.2. أوجد الزاوية بين المتجهات أ= 2م+4نو ب= م-ن، أين مو ن-ناقلات الوحدة والزاوية بينهما مو نيساوي 120 س.
حل. لدينا: كوس φ = أب/أب أب =(2م+4ن) (م-ن) = 2م 2 - 4ن 2 +2مليون=
= 2 - 4+2cos120 o = - 2 + 2(-0.5) = -3; أ = ; أ 2 = (2م+4ن) (2م+4ن) =
= 4م 2 +16مليون+16ن 2 = 4+16(-0.5)+16=12، مما يعني أ = . ب = ; ب 2 =
= (م-ن)(م-ن) = م 2 -2مليون+ن 2 =
1-2(-0.5)+1 = 3، مما يعني ب = . أخيرًا لدينا: cos φ == -1/2، φ = 120 o.
مثال 1.3.معرفة المتجهات أ.ب(-3،-2.6) و قبل الميلاد(-2،4،4)، احسب طول الارتفاع AD للمثلث ABC.
حل. بالدلالة على مساحة المثلث ABC بواسطة S، نحصل على:
ق = 1/2 ق.م. م. ثم AD=2S/BC، BC= = ![]() = 6,
= 6,
ق = 1/2| أ ب ×تكييف |. أس = أ ب + ق، وهو ما يعني ناقلات مكيف الهواءلديه إحداثيات
.
صفحة 1 من 2
السؤال رقم 1.ما هو المتجه؟ كيف يتم تعيين المتجهات؟
إجابة.سوف نسمي الجزء الموجه بالمتجه (الشكل 211). يتم تحديد اتجاه المتجه من خلال الإشارة إلى بدايته ونهايته. في الرسم، يتم الإشارة إلى اتجاه المتجه بواسطة سهم. للدلالة على المتجهات سنستخدم الحروف اللاتينية الصغيرة a، b، c، .... يمكنك أيضًا الإشارة إلى المتجه من خلال الإشارة إلى بدايته ونهايته. في هذه الحالة، يتم وضع بداية المتجه في المقام الأول. بدلاً من كلمة "ناقل"، يتم أحيانًا وضع سهم أو خط فوق تعيين حرف المتجه. يمكن الإشارة إلى المتجه في الشكل 211 على النحو التالي:
\(\overline(a)\)، \(\overrightarrow(a)\) أو \(\overline(AB)\)، \(\overrightarrow(AB)\).
السؤال 2.ما هي المتجهات التي تسمى موجهة بشكل مماثل (موجهة بشكل معاكس)؟
إجابة.يُقال إن المتجهات \(\overline(AB)\) و \(\overline(CD)\) موجهة بشكل متساوٍ إذا كان الخطان النصفيان AB وCD موجهان بشكل متساوٍ.
يُقال إن المتجهات \(\overline(AB)\) و \(\overline(CD)\) موجهة بشكل معاكس إذا كان الخطان النصفيان AB وCD موجهان بشكل معاكس.
في الشكل 212، يتم توجيه المتجهين \(\overline(a)\) و \(\overline(b)\) بالتساوي، والمتجهان \(\overline(a)\) و \(\overline(c)\ ) موجهة بشكل معاكس.

السؤال 3.ما هو الحجم المطلق للمتجه؟
إجابة.القيمة المطلقة (أو المعامل) للمتجه هي طول القطعة التي تمثل المتجه. تتم الإشارة إلى القيمة المطلقة للمتجه \(\overline(a)\) بواسطة |\(\overline(a)\)|.
السؤال 4.ما هو ناقلات فارغة؟
إجابة.يمكن أن تتزامن بداية المتجه مع نهايته. سوف نسمي هذا المتجه بالمتجه الصفري. تتم الإشارة إلى المتجه الصفري بصفر بشرطة (\(\overline(0)\)). لا يتحدثون عن اتجاه المتجه الصفري. تعتبر القيمة المطلقة للمتجه الصفري مساوية للصفر.
السؤال 5.ما هي المتجهات التي تسمى متساوية؟
إجابة.يقال أن المتجهين متساويان إذا تم دمجهما عن طريق الترجمة المتوازية. هذا يعني أن هناك ترجمة متوازية تأخذ بداية ونهاية متجه واحد إلى بداية ونهاية متجه آخر، على التوالي.
السؤال 6.أثبت أن المتجهات المتساوية لها نفس الاتجاه ومتساوية في القيمة المطلقة. والعكس صحيح: المتجهات المتماثلة الاتجاه والمتساوية في القيمة المطلقة تكون متساوية.
إجابة.أثناء الترجمة المتوازية، يحتفظ المتجه باتجاهه، بالإضافة إلى قيمته المطلقة. وهذا يعني أن المتجهات المتساوية لها نفس الاتجاهات ومتساوية في القيمة المطلقة.
دع \(\overline(AB)\) و\(\overline(CD)\) يكونان متجهين متماثلين، متساويين في القيمة المطلقة (الشكل 213). الترجمة المتوازية التي تنقل النقطة C إلى النقطة A تجمع بين نصف السطر CD مع نصف السطر AB، حيث أنهما لهما نفس الاتجاه. وبما أن القطعتين AB وCD متساويتان، فإن النقطة D تتزامن مع النقطة B، أي. تقوم الترجمة المتوازية بتحويل المتجه \(\overline(CD)\) إلى المتجه \(\overline(AB)\). هذا يعني أن المتجهين \(\overline(AB)\) و \(\overline(CD)\) متساويان، وهو ما يجب إثباته.

السؤال 7.أثبت أنه من أي نقطة يمكنك رسم متجه يساوي متجهًا معينًا، وواحدًا فقط.
إجابة.دع القرص المضغوط يكون خطًا، ويكون المتجه \(\overline(CD)\) جزءًا من السطر المضغوط. اجعل AB هو الخط المستقيم الذي ينتقل إليه القرص المضغوط للخط المستقيم أثناء النقل المتوازي، ويكون \(\overline(AB)\) هو المتجه الذي ينتقل إليه المتجه \(\overline(CD)\) أثناء النقل المتوازي، وبالتالي فإن المتجهات \(\ overline(AB)\) و \(\overline(CD)\) متساوية، والخطوط المستقيمة AB وCD متوازية (انظر الشكل 213). كما نعلم، من خلال نقطة لا تقع على خط معين، من الممكن رسم خط مستقيم واحد على الأكثر موازيًا للخط المعطى (بديهية الخطوط المتوازية). وهذا يعني أنه من خلال النقطة A يمكن رسم خط واحد موازيًا للخط CD. نظرًا لأن المتجه \(\overline(AB)\) جزء من الخط AB، فيمكن من خلال النقطة A رسم متجه واحد \(\overline(AB)\)، يساوي المتجه \(\overline(CD)\ ).
السؤال 8.ما هي إحداثيات المتجهات؟ ما القيمة المطلقة للمتجه الذي إحداثياته a 1، a 2؟
إجابة.دع المتجه \(\overline(a)\) له نقطة بداية A 1 (x 1 ; y 1)، ونقطة نهاية A 2 (x 2 ; y 2). إحداثيات المتجه \(\overline(a)\) ستكون الأرقام a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . سنضع إحداثيات المتجه بجوار حرف المتجه، في هذه الحالة \(\overline(a)\) (a 1 ; a 2) أو ببساطة \(\overline(a 1 ; a 2 ) )\). إحداثيات المتجه الصفري تساوي الصفر.
من الصيغة التي تعبر عن المسافة بين نقطتين من خلال إحداثياتهما، يترتب على ذلك أن القيمة المطلقة للمتجه ذو الإحداثيات a 1 , a 2 تساوي \(\sqrt(a^2 1 + a^2 2 )\).
السؤال 9.أثبت أن المتجهات المتساوية لها إحداثيات متساوية على التوالي، والمتجهات ذات الإحداثيات المتساوية على التوالي متساوية.
إجابة.اجعل A 1 (x 1 ; y 1) و A 2 (x 2 ; y 2) بداية ونهاية المتجه \(\overline(a)\). بما أن المتجه \(\overline(a)\) الذي يساويه يتم الحصول عليه من المتجه \(\overline(a)\) عن طريق الترجمة المتوازية، فإن بدايته ونهايته ستكون A" 1 (x 1 + c; y 1 + d) على التوالي )، A" 2 (x 2 + c؛ y 2 + d). وهذا يوضح أن كلا المتجهين \(\overline(a)\) و \(\overline(a")\) لهما نفس الإحداثيات: س 2 - س 1، ص 2 - ص 1.
دعونا الآن نثبت البيان العكسي. دع الإحداثيات المقابلة للمتجهين \(\overline(A 1 A 2 )\) و \(\overline(A" 1 A" 2 )\) متساوية. دعونا نثبت أن المتجهات متساوية.
اجعل x" 1 و y" 1 هما إحداثيات النقطة A" 1، و x" 2، y" 2 هما إحداثيات النقطة A" 2. وفقًا لشروط النظرية، x 2 - x 1 = x" 2 - x" 1, y 2 - y 1 = y" 2 - y" 1. وبالتالي x" 2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. النقل الموازي الذي تعطى بواسطة الصيغ
x" = x + x" 1 - x 1 , y" = y + y" 1 - y 1 ,
ينقل النقطة أ 1 إلى النقطة أ" 1، والنقطة أ 2 إلى النقطة أ" 2، أي. المتجهات \(\overline(A 1 A 2 )\) و \(\overline(A" 1 A" 2 )\) متساوية، وهو ما يجب إثباته.
السؤال 10.تحديد مجموع المتجهات.
إجابة.مجموع المتجهات \(\overline(a)\) و \(\overline(b)\) بالإحداثيات a 1 و a 2 و b 1 , b 2 يسمى المتجه \(\overline(c)\) مع الإحداثيات أ 1 + ب 1، أ 2 + ب أ 2، أي.
\(\الخط الفوقي(أ) (أ 1 ; أ 2) + \الخط الفوقي(ب)(ب 1 ; ب 2) = \الخط الفوقي(ج) (أ 1 + ب 1 ; أ 2 + ب 2)\).
تعريف
المتجه(من اللات." المتجه" - "الحمل") - قطعة موجهة من خط مستقيم في الفضاء أو على مستوى.
بيانياً، يتم تصوير المتجه كقطعة مستقيمة موجهة بطول معين. يُشار إلى المتجه الذي تكون بدايته عند نقطة ونهايته عند نقطة على أنه (الشكل 1). يمكن أيضًا الإشارة إلى المتجه بحرف صغير واحد، على سبيل المثال، .
إذا تم تحديد نظام إحداثي في الفضاء، فيمكن تحديد المتجه بشكل فريد من خلال مجموعة من إحداثياته. أي أن المتجه يُفهم على أنه كائن له حجم (طول) واتجاه ونقطة تطبيق (بداية المتجه).
ظهرت مبادئ حساب التفاضل والتكامل المتجه في أعمال عالم الرياضيات والميكانيكا والفيزيائي والفلكي والمساح الألماني يوهان كارل فريدريش غاوس (1777-1855) في عام 1831. تم نشر الأعمال المتعلقة بالعمليات باستخدام المتجهات من قبل عالم الرياضيات والميكانيكا والفيزياء النظرية الأيرلندي السير ويليام روان هاملتون (1805-1865) كجزء من حساب التفاضل والتكامل الرباعي. واقترح العالم مصطلح "المتجه" ووصف بعض العمليات على المتجهات. تم تطوير حساب التفاضل والتكامل المتجه بشكل أكبر بفضل العمل في مجال الكهرومغناطيسية الذي قام به الفيزيائي والرياضي والميكانيكي البريطاني جيمس كليرك ماكسويل (1831-1879). في ثمانينيات القرن التاسع عشر، نُشر كتاب “عناصر تحليل المتجهات” للفيزيائي والكيميائي الفيزيائي والرياضي والميكانيكي الأمريكي يوشيا ويلارد جيبس (1839-1903). تم وصف تحليل المتجهات الحديث في عام 1903 في أعمال العالم الإنجليزي والمهندس وعالم الرياضيات والفيزيائي أوليفر هيفيسايد (1850-1925).
تعريف
طولأو وحدة المتجهاتهو طول الجزء الموجه الذي يحدد المتجه. كما تدل .

الأنواع الرئيسية للنواقل
ناقل صفريسمى المتجه الذي تتطابق نقطة بدايته مع نقطة نهايته. طول المتجه الصفري هو صفر.
تسمى المتجهات الموازية لخط واحد أو التي تقع على خط واحد على استطراد(الصورة 2).
شارك في الإخراجإذا تطابقت اتجاهاتهم.
في الشكل 2 هذه هي المتجهات و. تتم الإشارة إلى الاتجاه المشترك للمتجهات على النحو التالي: .
يتم استدعاء متجهين خطيين متسامتين موجهة بشكل معاكسإذا كان اتجاههما متعاكسين.
في الشكل 3 هذه هي المتجهات و. تعيين: .
يعتبر هذا المفهوم كمتجه في جميع العلوم الطبيعية تقريبا، ويمكن أن يكون له معان مختلفة تماما، لذلك من المستحيل إعطاء تعريف لا لبس فيه للمتجه لجميع المجالات. ولكن دعونا نحاول معرفة ذلك. إذًا، ما هو المتجه؟
مفهوم المتجه في الهندسة الكلاسيكية
المتجه في الهندسة هو قطعة يُشار إليها في أي من نقاطها هي البداية وأيها هي النهاية. وهذا يعني، ببساطة، أن الجزء الموجه يسمى المتجه.
وفقًا لذلك، يتم الإشارة إلى المتجه (ما هو عليه - تمت مناقشته أعلاه)، بالإضافة إلى المقطع، أي بحرفين كبيرين من الأبجدية اللاتينية مع إضافة خط أو سهم يشير إلى اليمين في الأعلى. يمكن أيضًا توقيعه بحرف صغير (صغير) من الأبجدية اللاتينية بخط أو سهم. يشير السهم دائمًا إلى اليمين ولا يتغير حسب موقع المتجه.
وبالتالي، فإن المتجه له اتجاه وطول.
يحتوي تعيين المتجه أيضًا على اتجاهه. ويتم التعبير عن ذلك كما في الشكل أدناه.

يؤدي تغيير الاتجاه إلى عكس قيمة المتجه.
طول المتجه هو طول القطعة التي يتكون منها. يشار إليه على أنه معامل المتجه. وهذا يظهر في الصورة أدناه.

وبناء على ذلك، فإن المتجه الذي طوله صفر هو صفر. ويترتب على ذلك أن المتجه الصفري هو نقطة، وتتطابق نقطتي بدايته ونهايته.
طول المتجه يكون دائمًا كمية غير سالبة. بمعنى آخر، إذا كان هناك قطعة، فمن الضروري أن يكون لها طول معين أو أنها نقطة، فإن طولها يساوي صفرًا.
إن مفهوم النقطة في حد ذاته أساسي وليس له تعريف.
إضافة المتجهات
هناك صيغ وقواعد خاصة للمتجهات التي يمكن استخدامها لإجراء عملية الجمع.
حكم المثلث. لإضافة متجهات وفقًا لهذه القاعدة، يكفي الجمع بين نهاية المتجه الأول وبداية الثاني باستخدام الترجمة المتوازية، وربطهما. سيكون المتجه الثالث الناتج مساويًا لإضافة المتجهين الآخرين.
قاعدة متوازي الأضلاع. للإضافة باستخدام هذه القاعدة، عليك رسم كلا المتجهين من نقطة واحدة، ثم رسم متجه آخر من نهاية كل منهما. أي أنه سيتم سحب الثاني من المتجه الأول، والأول من المتجه الثاني. والنتيجة هي نقطة تقاطع جديدة ويتم تشكيل متوازي الأضلاع. إذا قمت بدمج نقطة تقاطع بدايات المتجهات ونهاياتها، فسيكون المتجه الناتج هو نتيجة الجمع.
يمكن أن يتم الطرح بطريقة مماثلة.
الفرق المتجهات
كما هو الحال مع جمع المتجهات، من الممكن أيضًا طرحها. ويستند إلى المبدأ الموضح في الشكل أدناه.

أي أنه يكفي تمثيل المتجه المطروح في شكل متجه معاكس له، وإجراء الحساب باستخدام مبادئ الجمع.
أيضًا، يمكن ضرب أي متجه غير الصفر بأي رقم k، وهذا سيغير طوله بمقدار k مرة.
بالإضافة إلى ذلك، هناك صيغ متجهة أخرى (على سبيل المثال، للتعبير عن طول المتجه من خلال إحداثياته).
موقع المتجهات
من المؤكد أن الكثيرين قد صادفوا مفهومًا مثل المتجه الخطي المتداخل. ما هي العلاقة الخطية المتداخلة؟
العلاقة الخطية المتداخلة للمتجهات تعادل توازي الخطوط. إذا كان هناك متجهان يقعان على مستقيمين متوازيين أو على نفس الخط، فإن هذه المتجهات تسمى خطية متداخلة.
اتجاه. فيما يتعلق ببعضها البعض، يمكن أن تكون المتجهات الخطية ذات اتجاه مشترك أو موجهة بشكل معاكس، ويتم تحديد ذلك من خلال اتجاه المتجهات. وبناءً على ذلك، إذا كان المتجه مشتركًا في الاتجاه مع آخر، فإن المتجه المقابل له يكون في اتجاه معاكس.
يوضح الشكل الأول متجهين متعاكسين الاتجاه، ومتجه ثالث ليس على خط مستقيم معهم.
بعد تقديم الخصائص المذكورة أعلاه، من الممكن تحديد ناقلات متساوية - وهي ناقلات موجهة في اتجاه واحد ولها نفس طول المقاطع التي تشكلت منها.
في العديد من العلوم، يتم استخدام مفهوم ناقل نصف القطر أيضًا. يصف هذا المتجه موضع نقطة واحدة على المستوى بالنسبة إلى نقطة ثابتة أخرى (غالبًا ما يكون هذا هو الأصل).
المتجهات في الفيزياء
لنفترض أنه عند حل مسألة ما، ظهرت حالة: يتحرك الجسم بسرعة 3 م/ث. وهذا يعني أن الجسم يتحرك في اتجاه معين على طول خط مستقيم واحد، وبالتالي فإن هذا المتغير سيكون كمية متجهة. لحل هذه المشكلة، من المهم معرفة كل من القيمة والاتجاه، لأنه اعتمادًا على الاعتبار، يمكن أن تكون السرعة إما 3 م/ث أو -3 م/ث.
بشكل عام، يتم استخدام المتجه في الفيزياء للإشارة إلى اتجاه القوة المؤثرة على الجسم وتحديد النتيجة.
عندما تتم الإشارة إلى هذه القوى في الشكل، تتم الإشارة إليها بواسطة أسهم تحمل علامة متجهة فوقها. من الناحية الكلاسيكية، فإن طول السهم له نفس القدر من الأهمية؛ فهو يستخدم للإشارة إلى القوة الأقوى، ولكن هذه خاصية ثانوية ولا ينبغي الاعتماد عليها.
المتجهات في الجبر الخطي وحساب التفاضل والتكامل
تسمى عناصر المسافات الخطية أيضًا بالمتجهات، ولكنها في هذه الحالة تمثل نظامًا مرتبًا من الأرقام التي تصف بعض العناصر. ولذلك، فإن الاتجاه في هذه الحالة لم يعد له أي أهمية. يختلف تعريف المتجه في الهندسة الكلاسيكية وحساب التفاضل والتكامل بشكل كبير.
إسقاط المتجهات
ناقلات المتوقعة - ما هو؟
في كثير من الأحيان، لإجراء حساب صحيح ومريح، من الضروري توسيع المتجه الموجود في مساحة ثنائية الأبعاد أو ثلاثية الأبعاد على طول محاور الإحداثيات. هذه العملية ضرورية، على سبيل المثال، في الميكانيكا عند حساب القوى المؤثرة على الجسم. يتم استخدام المتجه في كثير من الأحيان في الفيزياء.
لإجراء الإسقاط، يكفي خفض الخطوط المتعامدة من بداية ونهاية المتجه على كل محور من محاور الإحداثيات، وستسمى الأجزاء التي تم الحصول عليها عليها إسقاط المتجه على المحور.

لحساب طول الإسقاط، يكفي ضرب طوله الأصلي بوظيفة مثلثية معينة، والتي يتم الحصول عليها عن طريق حل مشكلة صغيرة. في الأساس، يوجد مثلث قائم الزاوية يكون فيه الوتر هو المتجه الأصلي، وأحد الأرجل هو المسقط، والساق الأخرى هي المتعامد المسقط.
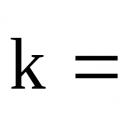 معدل التفاعل ثابت المبادئ التوجيهية للعمل المختبري
معدل التفاعل ثابت المبادئ التوجيهية للعمل المختبري هل هناك حياة بعد الموت؟
هل هناك حياة بعد الموت؟ علماء: الأرض “سجن فضائي” للإنسانية علماء: الأرض سجن فضائي في الكون
علماء: الأرض “سجن فضائي” للإنسانية علماء: الأرض سجن فضائي في الكون